Physiker wollen alle Phasen der Materie klassifizieren

Eine vollständige Klassifizierung kann zu einer Vielzahl neuer Materialien und Technologien führen. Die exotischsten Phasen widersetzen sich jedoch weiterhin dem Verständnis der Wissenschaftler

In den letzten drei Jahrzehnten haben Experten der Physik der kondensierten Materie ein wundervolles Land neuer, exotischer Phasen der Materie entdeckt: plötzlich auftretende kollektive Zustände wechselwirkender Teilchen, die sich völlig von den festen, flüssigen oder gasförmigen Zuständen der Materie unterscheiden, die jedem bekannt sind.

Diese Phasen treten, wie einige in Laboratorien verstanden haben und andere auf theoretischen Berechnungen beruhen, auf, wenn die Materie fast auf eine Temperatur von absolut Null abkühlt, die unter normalen Bedingungen mehr als zweihundert Grad unter dem Gefrierpunkt von Wasser liegt. Unter diesen kalten Bedingungen können Partikel auf eine Weise interagieren, die sie dazu bringt, alle Spuren ihrer früheren Identität zu verwerfen. Die Experimente der 1980er Jahre haben herausgefunden, dass Elektronen in einigen Situationen in Teilchenfraktionen aufgeteilt werden, die in Form von Geflechten Spuren in Raum-Zeit hinterlassen können. in anderen erscheinen masselose Versionen von sich selbst unter ihnen. Ein Gitter aus sich drehenden Atomen wird durch sich drehende Schleifen oder verzweigte Ketten flüssig; Kristalle, die anfangs keine Elektrizität leiteten, beginnen, Strom über die Oberfläche zu leiten. Eine der Phasen, die Experten schockierte, als es 2011 erstmals mathematisch bewiesen wurde , umfasst sehr seltsame Entitäten, „ Fraktons “, die in fraktalen Mustern miteinander verzahnt sind [laut Wiki sind Fraktone ein fraktales Analogon von Phononen , Quanten der Schwingungsbewegung von Atomen Kristall / ca. übersetzt.].

Jetzt konkurrieren Forschungsteams von Microsoft und anderen Unternehmen darum, Quanteninformationen in Pigtails und Schleifen einiger dieser Phasen zu schreiben, um einen Quantencomputer zu entwickeln. Inzwischen haben Theoretiker der Physik der kondensierten Materie (CS) kürzlich mehrere Studien durchgeführt, die für das Verständnis kollektiver Verhaltensschemata am wichtigsten sind, um alle möglichen Phasen der Materie zu nummerieren und zu klassifizieren. Wenn es ihnen gelingt, eine vollständige Klassifizierung zu erstellen, können nicht nur alle in der Natur in der Natur vorkommenden Phasen der Materie beschrieben werden, sondern es kann auch der Weg aufgezeigt werden, wie neue Materialien und Technologien erhalten werden können.

Forscher, angeführt von Dutzenden der besten Theoretiker und mit Hilfe von Mathematikern, haben bereits ein ganzes Auto von Phasen klassifiziert, die in einer oder zwei räumlichen Dimensionen auftreten können , und sie mit der Topologie verknüpft: mit Mathematik, die die unveränderlichen Eigenschaften solcher Formen wie Kugel oder Torus beschreibt. Sie tauchten auch in den Dschungel der Phasen ein, die im Bereich des absoluten Nullpunkts in dreidimensionaler Materie entstehen.


Xi Chen, Theoretiker für kondensierte Materie am California Institute of Technology

Wissenschaftler suchen nach "keinem bestimmten Gesetz der Physik", sagte Michael Zaletel , ein FCC-Theoretiker an der Princeton University. "Sie suchen einen Raum mit allen Möglichkeiten, und dies ist in gewisser Weise eine tiefere und schönere Idee." Dies mag unerwartet sein, aber wie Zaletel sagt, ist der Raum aller konsistenten Phasen an sich ein mathematisches Objekt "mit einer unglaublich reichen Struktur, die, wie wir glauben, in der eindimensionalen und zweidimensionalen Welt eins zu eins mit diesen schönen topologischen Strukturen zusammenfällt". .

Es gibt eine "Ökonomie der Optionen" in der Landschaft aller Phasen ", sagte Ashvin Vishwanath von der Harvard University. "Und alles scheint erkennbar" - solches Glück verwirrt ihn. Die Nummerierung der Phasen der Materie könnte sich als "wie das Sammeln von Briefmarken" herausstellen, sagte Viswanath, "jede unterscheidet sich geringfügig von den anderen, und es gibt keine Verbindung zwischen ihnen." Stattdessen ähnelt die Phasenklassifizierung eher einem „Periodensystem“. Es gibt viele Elemente, aber sie sind in Kategorien unterteilt, und wir können diese Kategorien verstehen. “

Die Klassifizierung des manifestierten Verhaltens von Partikeln mag nicht so grundlegend erscheinen, aber einige Experten, beispielsweise Si- Gang Wen vom Massachusetts Institute of Technology, sagen, dass die neuen Regeln der manifestierten Phasen zeigen, wie Elementarteilchen selbst vor dem Hintergrund von entstehen können Sie basieren auf einem Netzwerk verschränkter Quanteninformationsbits, die Ven den "Ozean der Qubits" nennt. Beispielsweise sehen in der Phase " String-Netzwerk-Fluid ", die sich in einem dreidimensionalen System von Qubits manifestieren kann, Störungen genau wie die bekannten Elementarteilchen aus. "Ein echtes Elektron und ein echtes Proton können nur Schwankungen im String-Netzwerk sein", sagt Ven.

Neue topologische Ordnung

Bevor diese Phasen plötzlich bei Nulltemperatur auftraten, glaubten die Physiker, dass ihnen alle Phasen bereits bekannt waren. Bereits in den 1950er Jahren konnten sie erklären, was zum Beispiel passiert, wenn sich Wasser in Eis verwandelt, und es als Verletzung der Symmetrie beschreiben: Wenn flüssiges Wasser auf atomarer Ebene Rotationssymmetrie aufweist (in alle Richtungen gleich), dann die Eismoleküle H. ₂ O sind in Spalten und Zeilen eingeschlossen.

Alles änderte sich 1982 nach der Entdeckung des fraktionierten Quanten-Hall-Effekts , der sich in einem ultrakalten zweidimensionalen Elektronengas manifestiert. Eine Substanz in diesem Zustand besaß manifestierende Teilchen mit Ladungen in einem Bruchteil der Ladungen eines Elektrons, wodurch bei einem einseitigen Umgehen des Systemumfangs Bruchteile von Schritten entstanden. "Mit Symmetrie war es bereits unmöglich, zwischen diesen Phasen zu unterscheiden", sagte Ven.

Ein neues Paradigma wurde benötigt. 1989 führte Ven ein, dass solche Phasen wie der Zustand des fraktionierten Quanten-Hall-Effekts nicht in der Ebene auftreten, sondern auf anderen topologischen Mengen - verbundenen Oberflächen wie der Oberfläche einer Kugel oder eines Torus. Die Topologie bezieht sich auf die globalen, unveränderlichen Eigenschaften solcher Räume, die durch lokale Verformung nicht verändert werden können. Wie Sie wissen, können Sie zumindest für Topologen einen Donut in einen Becher verwandeln, indem Sie seine Oberfläche verformen, da beide Figuren ein Loch haben und daher topologisch gleichwertig sind. Aber dehnen und drücken Sie so viel, wie Sie möchten, und selbst der flexibelste Donut kann nicht in eine Brezel verwandelt werden.

Ven entdeckte, dass unter neuen topologischen Bedingungen neue Eigenschaften bei Phasen mit Nulltemperatur auftreten, und prägte den Begriff " topologische Ordnung ", der das Wesen dieser Phasen beschreibt. Andere Theoretiker entdeckten ebenfalls einen Zusammenhang zwischen Phasen und Topologie. Mit der Entdeckung vieler verschiedener exotischer Phasen - es gibt so viele von ihnen, dass Forscher sagen, dass sie kaum mithalten können - wurde klar, dass Topologie und Symmetrie ein gutes System für ihre Organisation bieten.

Topologische Phasen treten nur im Bereich des absoluten Nullpunkts auf, da Partikelsysteme nur bei so niedrigen Temperaturen mit der niedrigsten Energie in den Grundquantenzustand eintreten können. Im Grundzustand binden empfindliche Wechselwirkungen, die die Identität der Partikel bestimmen und bei hohen Temperaturen verschwinden, die Partikel mithilfe von Quantenverschränkung in globale Systeme. Anstatt Teilchen einzeln zu beschreiben, werden sie mathematisch zu Komponenten einer komplexeren Funktion, die sie alle gleichzeitig beschreibt, häufig mit dem Aufkommen neuer Teilchen in Form globaler Phasenanregungen. Die aufkommenden Schemata der Fernverschränkung erweisen sich als topologisch, dh unempfindlich gegenüber lokalen Störungen - wie die Anzahl der Löcher in einem Satz.


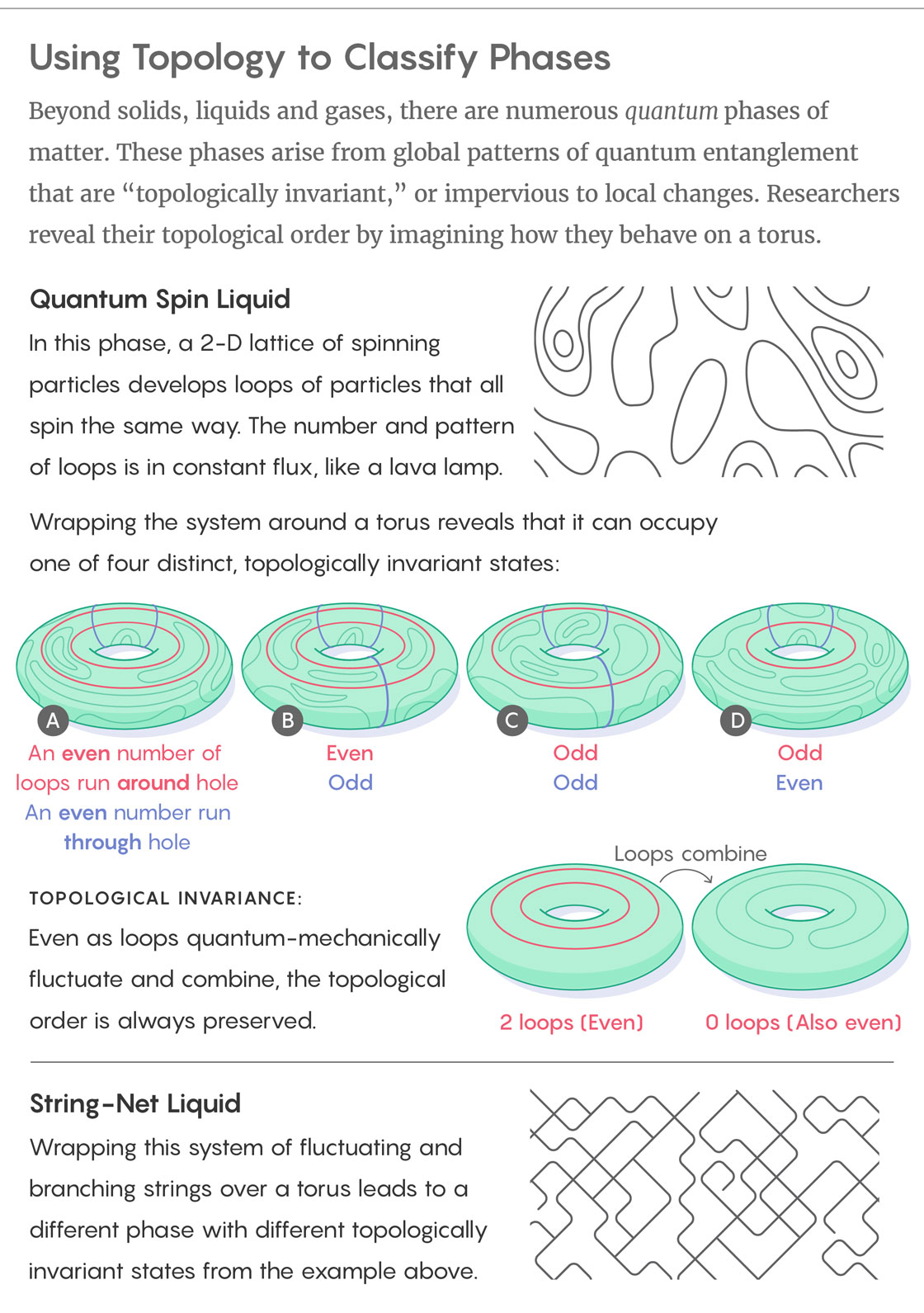Oben: Quantenflüssigkeits-Spinphase. In dieser Phase führt ein zweidimensionales Gitter rotierender Partikel zum Auftreten von gleich rotierenden Partikelschleifen. Die Anzahl und Anordnung der Schleifen ändert sich ständig, und all dies ähnelt einer Lavalampe .

Wenn Sie dieses System auf einen Torus wickeln, stellt sich heraus, dass es vier verschiedene topologisch invariante Zustände einnehmen kann:
A) Um das Loch herum: gerade Anzahl von Schleifen / Durchgangsloch: gerade Anzahl von Schleifen.
B) Gerade / Ungerade.
C) Ungerade / Ungerade.
D) Ungerade / Gerade.

Trotz der Tatsache, dass die Schleifen ständig quantenmechanischen Schwankungen unterliegen, bleibt die topologische Reihenfolge immer erhalten (2 Schleifen können zu 0 Schleifen gehen, was ebenfalls eine gerade Zahl ist).

Unten: String-Netzwerkflüssigkeit. Wenn wir einen Torus mit einem System aus wechselnden und verzweigten Strings umwickeln, erhalten wir auch verschiedene topologisch invariante Zustände.

Betrachten Sie die einfachste topologische Phase eines Systems, das als "Quantenspinfluid" bezeichnet wird und aus einem zweidimensionalen Gitter von Spins oder Partikeln besteht, die nach oben, unten oder mit einiger Wahrscheinlichkeit gleichzeitig in beide Richtungen zeigen. Bei einer Temperatur von Null erzeugt Spin-Liquid Spins-Strings, die in eine Richtung nach unten zeigen, und diese Strings bilden geschlossene Schleifen. Die Richtung der Spins unterliegt quantenmechanischen Schwankungen, und auch das Muster der Schleifen auf dem Material ändert sich: Die Schleifen der unteren Spins werden zu größeren Schleifen kombiniert oder in kleinere aufgeteilt. In einer solchen Phase eines Quantenspinfluids ist der Grundzustand des Systems eine Quantenüberlagerung aller möglichen Schleifenmuster.

Um zu verstehen, warum dieses Verschränkungsschema eine topologische Ordnung ist, stellen Sie sich vor, wie Ven es getan hat, dass die Flüssigkeit der Quantenspins über die Oberfläche eines Torus fließt und einige der Schleifen sich um seine Öffnung drehen. Aus diesem Grund existiert anstelle eines Grundzustands, der einer Überlagerung aller Schleifenmuster zugeordnet ist, ein Spinfluid in einem von vier verschiedenen Grundzuständen, die vier Überlagerungen von Schleifenmustern zugeordnet sind. Ein Zustand besteht aus allen möglichen Schleifenmustern mit einer geraden Anzahl von Schleifen, die das Loch des Torus umgeben, und einer geraden Anzahl von Schleifen, die durch dieses Loch verlaufen. Die andere hat die erste gerade und die zweite ungerade Zahl; Die dritte und vierte haben diese Zahlen jeweils ungerade / gerade und ungerade / ungerade.

Und in einem dieser Zustände bleibt das System darin, obwohl sich das Schleifenmuster ständig lokal ändert. Wenn zum Beispiel die Spinflüssigkeit eine gerade Anzahl von Schleifen hat, die das Loch des Torus umgeben, können sich diese beiden Schleifen berühren und miteinander verbinden und sich plötzlich in eine Schleife verwandeln, die das Loch überhaupt nicht umgibt. Die Anzahl der Schleifen wird um zwei reduziert, bleibt aber immer noch gerade. Der Grundzustand des Systems ist eine topologisch invariante Eigenschaft, die gegen lokale Veränderungen resistent ist.

Quantencomputer der Zukunft können diese Invarianz nutzen. Wenn Sie vier topologische Grundzustände haben, die unabhängig von lokalen Störungen oder Fehlern sind, „haben Sie eine Möglichkeit, Quanteninformationen zu speichern, da Ihr Bit möglicherweise anzeigt, in welchem ​​Zustand Sie sich befinden“, erklärt Zaletel, der die topologischen Eigenschaften von Spinflüssigkeiten und untersucht hat andere Quantenphasen. Systeme wie Spin-Fluid müssen sich nicht um einen Torus wickeln, um topologisch geschützte Grundzustände zu haben. Die Lieblingssandbox der Forscher ist der „ Toroidal Code “, eine Phase, die 1997 vom FCC-Theoretiker Alexei Kitaev vom California Institute of Technology theoretisch konstruiert und in Experimenten der letzten zehn Jahre demonstriert wurde. Ein Toroidcode kann in einer Ebene existieren und dennoch mehrere Grundzustände unterstützen, die der Oberfläche eines Torus inhärent sind. Tatsächlich können sich die Spin-Loops von einer Kante des Systems verschieben und an der anderen Kante erscheinen, und die um das System verdrillten Loops entsprechen den Loops um das Torusloch. "Wir wissen, wie man Verbindungen zwischen den Eigenschaften der Grundzustände des Systems auf dem Torus und dem entsprechenden Verhalten der Partikel herstellt", sagte Zaletel.

Spinflüssigkeiten können sich in anderen Phasen befinden, in denen die Spins keine geschlossenen Schleifen bilden, sondern sich verzweigen und ein Netzwerk von Strings bilden. Dies ist eine flüssige Phase mit einem String-Netzwerk , die laut Wien „das gesamte Standardmodell“ der Teilchenphysik ausgeben kann, beginnend mit einem dreidimensionalen Ozean von Qubits.

Universum der Phasen

Studien, die 2009 und 2010 von mehreren Gruppen durchgeführt wurden, vervollständigten die Klassifizierung der „isolierten“ Phasen der Materie, die sich in einer Dimension bilden - Partikelketten. Die isolierte Phase befindet sich im Grundzustand: Dieser Niedrigenergiezustand ist weit genug von den Hochenergiezuständen entfernt, so dass sich das System in diesem Zustand stabil niederlässt. Nur in isolierten Quantenphasen entstehen wohldefinierte Anregungen in Form von Partikeln. Ungetrennte Phasen sind brodelnde Quantensuppen, deren Eigenschaften größtenteils unerforscht bleiben.

Für eine eindimensionale Kette von Bosonen - Teilchen wie Photonen mit einem ganzzahligen Quantenspin (was bedeutet, dass sie nach dem Austausch in ihren ursprünglichen Zustand zurückkehren) gibt es nur eine isolierte topologische Phase. In dieser Phase, die erstmals vom Princeton-Theoretiker Duncan Haldein untersucht wurde , der 2016 mit David Thowless und John Michael Kosterlitz den Nobelpreis für jahrzehntelange Arbeiten an topologischen Phasen erhielt, erzeugt eine Spin-Kette Partikel mit einem halbzahligen Spin an beiden Enden. Die Kette von Fermionen hat zwei getrennte topologische Phasen (dies sind Teilchen wie Elektronen und Quarks mit halbzahligen Spins - was bedeutet, dass ihr Zustand negativ wird, wenn die Positionen geändert werden). Die topologische Ordnung in diesen eindimensionalen Ketten wächst nicht durch weitreichende Verschränkung, sondern durch lokale Symmetrie, die benachbarte Teilchen verbindet. Diese Phasen werden als "symmetrisch geschützte topologische Phasen" bezeichnet und entsprechen "Zyklen kohomologischer Gruppen ", mathematischen Objekten, die mit Invarianten wie der Anzahl der Löcher in der Menge assoziiert sind.


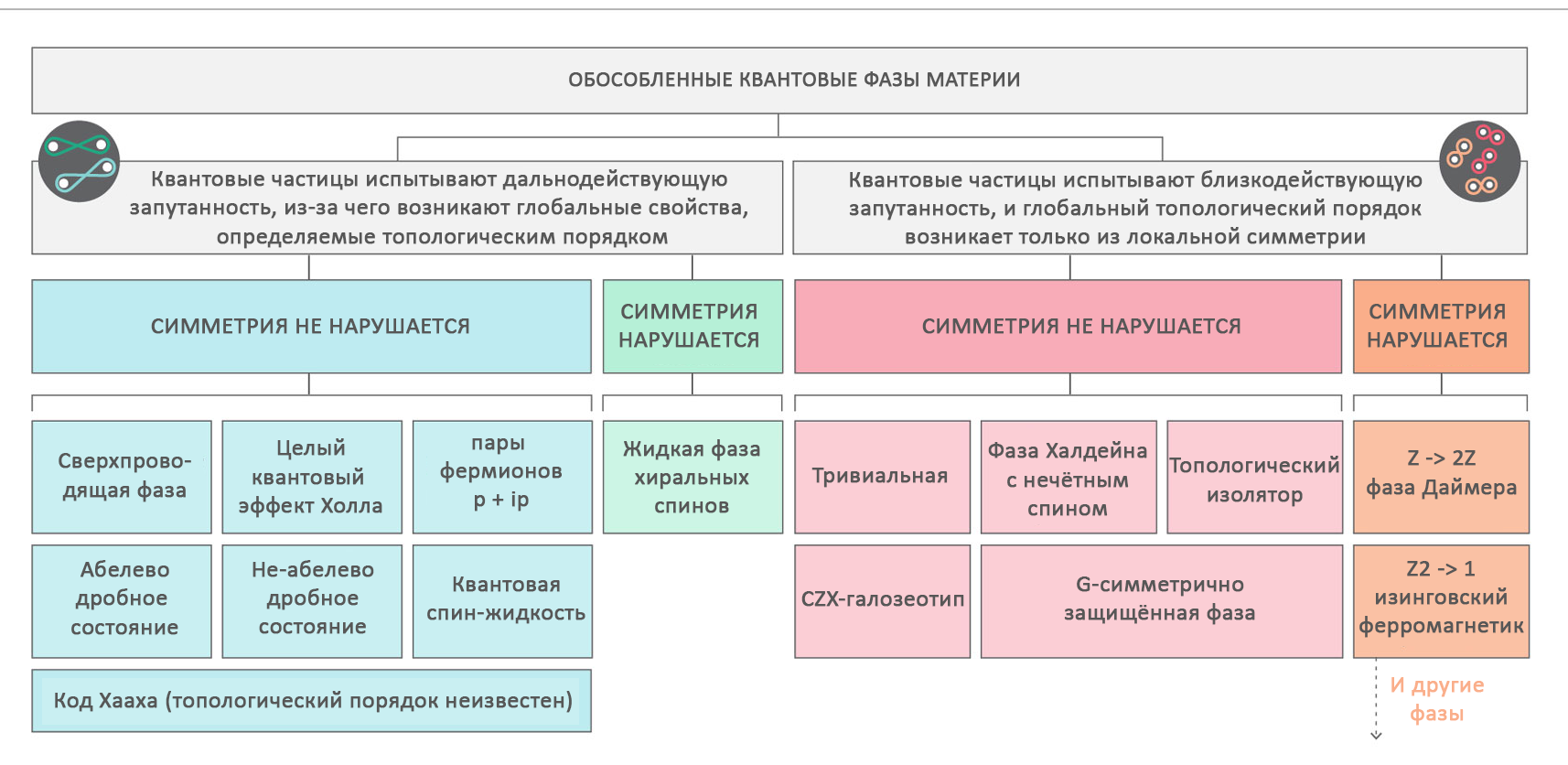Periodensystem der Phasen: Die Tabelle zeigt typische Beispiele für isolierte Phasen mit einem stabilen Grundzustand. Die Klassifizierung gilt für eindimensionale und zweidimensionale Räume als vollständig. Für dreidimensionale Räume ist wenig bekannt.

Zweidimensionale Phasen sind viel größer und viel interessanter. Sie können das manifestieren, was einige Experten für die „wahre“ topologische Ordnung halten: die Ordnung, die mit einer weitreichenden Quantenverschränkung verbunden ist, wie z. B. Schleifenschwankungen in einer Spinflüssigkeit. In den letzten Jahren haben Forscher gezeigt, dass diese Verschränkungsmuster topologischen Strukturen entsprechen, die als Tensorkategorien bezeichnet werden , und verschiedene Arten nummerieren, wie Objekte zusammengeführt und umeinander gewickelt werden können. "Tensorkategorien bieten eine Möglichkeit, Partikel zu beschreiben, die konsistent verschmelzen und flechten", sagte David Perez-Garcia von der Complutense-Universität Madrid.

Forscher wie Perez Garcia arbeiten an einem mathematischen Beweis dafür, dass die bekannten Klassen zweidimensionaler isolierter topologischer Phasen vollständig sind. Er half 2010 mit dem Abschluss eindimensionaler Klassen , wobei er die allgemein anerkannte Überzeugung verwendete, dass diese Phasen durch Quantenfeldtheorien immer gut angenähert werden - mathematische Beschreibungen, in denen die Umgebung, in der Quantenteilchen existieren, als glatt angesehen wird. "Diese Tensorkategorien decken hypothetisch alle zweidimensionalen Phasen ab, aber bisher gibt es keinen genauen mathematischen Beweis", sagte Perez-Garcia. - Natürlich wäre es viel interessanter, wenn nachgewiesen werden könnte, dass dies nicht alle Phasen sind. Exotische Dinge sind immer interessanter, weil sie eine neue Physik haben und nützlich sein können. "

Nicht isolierte Quantenphasen stellen einen weiteren Bereich des Untersuchungspotentials dar, sind jedoch von Nebel umgeben, der für die meisten theoretischen Methoden undurchlässig ist. "Wir können die Sprache der Teilchen nicht sprechen und stehen vor sehr ernsten Schwierigkeiten", sagt Senthil Todadri , Theoretiker von CS am MIT. Nicht isolierte Phasen dienen beispielsweise als Haupthindernis für das Verständnis der Hochtemperatursupraleitung. Sie erschweren das Leben von Quantengravitationsforschern, die sich der Bewegung „Alle Qubits“ angeschlossen haben und glauben, dass nicht nur Elementarteilchen, sondern auch Raum-Zeit und Schwerkraft aufgrund von Verschränkungsmustern im zugrunde liegenden Qubit-Ozean auftreten. "Wir verbringen viel Zeit damit, mit nicht isolierten Zuständen in" allen Qubits "zu arbeiten, weil von dort aus die Schwerkraft auftritt - zumindest denken wir das momentan", sagte Brian Swingle , ein theoretischer Physiker an der University of Maryland. Einige Forscher versuchen, das mathematische Prinzip der Dualität zu verwenden, um das Bild einer Quantensuppe in eine äquivalente Beschreibung von Partikeln zu verwandeln, die in einer höheren Dimension hergestellt wurden. "Dies sollte als Erkundung neuer Gebiete gesehen werden", sagt Todadri.

Die noch größere Begeisterung der Forscher zeigt sich im dreidimensionalen Raum. Bisher ist klar, dass unvorstellbar seltsame Systeme der Quantenverschränkung auftreten, wenn Spins und Partikel aus den Fesseln der Zweidimensionalität befreit werden und den dreidimensionalen Raum der Realität füllen. „Bisher gibt es Dinge in drei Dimensionen, die sich den Tensorkategorien entziehen“, sagt Perez-Garcia. "Die Aufregung [der Felder] ist völlig wild."

Haah Code

Und die wildeste der dreidimensionalen Phasen erschien vor sieben Jahren.Ein talentierter Caltech-Absolvent, Jeongwan Haah, entdeckte es mit einer Computersimulation, als er nach einem „ Traumcode “ suchte: einem grundlegenden Quantenzustand, der zuverlässig genug ist, um den Quantenspeicher auch bei Raumtemperatur sicher zu speichern.

Dafür musste sich Haah drei Dimensionen zuwenden. In zweidimensionalen topologischen Phasen wie einem Toroidcode wird ein erheblicher Teil der Fehler von den „stringartigen Operatoren“ eingeführt: Störungen im System, die zur zufälligen Bildung von Spinstrings führen. Diese Strings können manchmal neue Schleifen um das Torusloch wickeln, die Anzahl der Schleifen von gerade zu ungerade und umgekehrt ändern und den Toroidcode in einen der anderen drei Quantenzustände umwandeln. Da die Saiten unkontrolliert wachsen und sich um alles andere wickeln, sagen Experten, dass in einer zweidimensionalen Welt kein gutes Quantengedächtnis aufgebaut werden kann.


Jionwan Haah

Haach hat einen dreiphasigen Phasensuchalgorithmus geschrieben, der stringartige Operatoren vermeidet. Der Computer gab 17 genaue Lösungen heraus, die er dann manuell überprüfte. Es wurde bestätigt, dass die vier Phasen frei von stringartigen Operatoren sind. Eine der Phasen mit der größten Symmetrie wurde als Haach-Code bekannt.

Haahs Code ist möglicherweise nützlich zum Speichern von Quantenspeicher, aber gleichzeitig furchtbar seltsam. Xiao Chen, ein FCC-Theoretiker von Caltech, erinnert sich an die Nachricht als Doktorand im Jahr 2011, ein oder zwei Monate nach der verwirrenden Entdeckung von Haah. "Alle waren schockiert", sagt sie. "Wir wussten nicht, ob wir etwas dagegen tun können." Und heute besteht diese Situation seit vielen Jahren. "

Der Haach-Code auf Papier ist recht einfach: Er ist eine Lösung einer Energiegleichung mit zwei Begriffen, die Spins beschreibt, die mit acht ihrer nächsten Nachbarn in einem kubischen Gitter interagieren. Aber die daraus resultierende Phase "belastet unsere Vorstellungskraft", sagte Todadri.

Das Merkmal des Codes sind partikelähnliche Entitäten, Fraktons, die im Gegensatz zu Schleifenmustern in Quantenspinflüssigkeiten nicht flüssig sind und an Ort und Stelle ruhen; Fraktone können nur zwischen ihren Positionen im Gitter springen, wenn diese Positionen wie ein fraktales Muster behandelt werden. Das heißt, um zum Beispiel die an den Eckpunkten des Tetraeders stehenden Fraktone zum Austausch von Orten zu zwingen, ist es notwendig, Energie in jeden Eckpunkt des Systems zu gießen; Wenn Sie jedoch die Skala erhöhen, stellt sich heraus, dass das, was wir als Peak angesehen haben, tatsächlich die vier Eckpunkte des kleineren feineren Tetraeders sind, und wir müssen auch Energie in all diese Eckpunkte gießen. Wir zoomen immer noch hinein und finden wieder ein noch kleineres Tetraeder und so weiter. Dieses fraktale Verhalten bedeutet, dass der Haah-Code das zugrunde liegende Gitter niemals vergisst.und es kann nicht durch eine glatte Beschreibung des Gitters angenähert werden, wie es in der Quantenfeldtheorie getan wird. Darüber hinaus wächst die Anzahl der Grundzustände des Haach-Codes mit der Größe des an der Basis liegenden Gitters - und diese Eigenschaft ist definitiv nicht topologisch (wenn Sie einen Torus strecken, bleibt er immer noch ein Torus).

Der Quantenzustand des Haach-Codes ist äußerst stabil, da es unwahrscheinlich ist, dass ein fraktaler Operator, der für ihn ideal ist, zufällig erscheint. Experten sagen, dass die implementierte Version dieses Codes aus technologischer Sicht von großem Interesse sein kann.

Die Haah-Phase hat eine Welle theoretischer Überlegungen ausgelöst. Haah half dabei, als er 2015 mit zwei Kollegen vom MIT viele Beispiele in der Phasenklasse entdeckte, die heute als „Fraktonmodelle“ bekannt sind und die Verwandten des Haach-Codes vereinfachten. Das erste Modell dieser Familie wurde 2005 von Claudio Chamon von der Boston University vorgestellt. Chen und andere Wissenschaftler untersuchten die Topologie von Fraktonsystemen, von denen einige es Partikeln ermöglichen, sich entlang von Linien oder Ebenen im dreidimensionalen Raum zu bewegen, wodurch sie zu einem konzeptionellen Verständnis des Geschehens beitragen können oder für die experimentelle Implementierung besser geeignet sind. "Dies eröffnet einen Weg zu vielen weiteren exotischen Dingen", sagt Chen über den Haah-Code. - Dies ist eine Demonstration, wie wenig wir über die dreidimensionale Welt und höhere Dimensionen wissen.Und da wir noch kein systematisches Bild davon haben, was passiert, warten wir auf viele Entdeckungen aller Art.

Bisher weiß niemand, zu welchem ​​Teil der Landschaft möglicher Phasen der Haach-Code und seine Verwandten gehören oder wie groß der Raum der Möglichkeiten sein könnte. Laut Todadri hat die Community Fortschritte bei der Klassifizierung der einfachsten isolierten dreidimensionalen Phasen erzielt, aber es sind weitere Untersuchungen erforderlich, bevor das vollständige Klassifizierungsprogramm beginnt. Ihm zufolge ist es klar, dass "wenn wir die isolierten Phasen der Materie im dreidimensionalen Raum klassifizieren, wir uns solchen seltsamen Möglichkeiten stellen müssen, von denen eine zuerst von Haah entdeckt wurde".

Viele Forscher glauben, dass neue Klassifizierungskonzepte erforderlich sein könnten, um die fraktale Natur des Haach-Codes zu beschreiben und das gesamte Spektrum der Möglichkeiten dreidimensionaler Quantenmaterie zu entdecken. Ven sagte: "Wir brauchen eine neue Art von Theorie, eine neue Denkweise." Vielleicht, sagte er, brauchen wir ein neues Bild der nicht fließenden Systeme der langfristigen Beteiligung. "Wir haben einige allgemeine Ideen, aber es gibt keine systematische Mathematik für ihre Umsetzung", sagte er. - Wir haben ein gewisses Gefühl dafür, wie es aussieht. Eine detaillierte Systematisierung reicht nicht aus. Aber das ist aufregend. “