Passage der Venus auf der Sonnenscheibe und Bestimmung der Entfernung zwischen ihnen

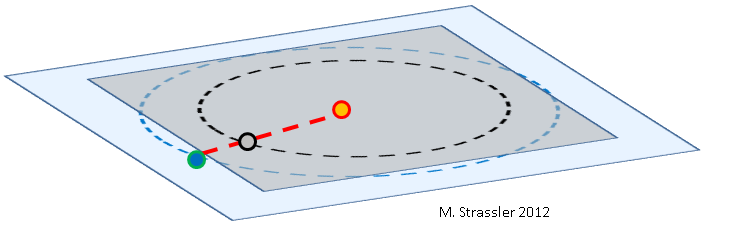
Abb. 1: Erde (blau), Venus (grau) und Sonne (orange), nicht maßstabsgetreu.

In Bezug auf den Durchgang der Venus durch die Sonnenscheibe im Jahr 2012 wurden bereits viele Artikel geschrieben. Wie selten und warum genau dieses Ereignis auftritt: Theoretisch sollte sich die Venus, die sich häufiger als die Erde um die Sonne bewegt, während jeder ihrer Umdrehungen zwischen Erde und Sonne bewegen (Abb. 1), aber weil Die Umlaufbahnen zweier Planeten sind nicht ausgerichtet (sie befinden sich nicht in derselben Ebene, siehe Abb. 2). Die Venus bewegt sich häufig vom Standpunkt der Erde aus über oder unter der Sonne.

Aber anstatt die Worte anderer zu wiederholen, möchte ich einige Details hinzufügen, die im Internet nicht so leicht zu finden sind.

Sie haben vielleicht gelesen, dass mit der Technik, die auf den Überlegungen des Astronomen Edmund Halley (des berühmten Kometen Halley) von 1678 bis 1716 sowie von James Gregory vor ihm basiert, die Passage der Venus 1716 verwendet wurde, um die Entfernung von der Erde zur Erde zu bestimmen Die Sonne (und vor der Venus und allen anderen Planeten) mit einem Fehler von 2% ist die höchste der zu diesem Zeitpunkt erreichten. Es wurde gehofft, dass die Genauigkeit zehnmal höher sein würde, aber ein unerwarteter optischer Effekt, der als „ Black Drop-Effekt “ bezeichnet wird, griff in den Prozess ein - es gibt immer noch Debatten über die genauen Gründe für sein Auftreten. Aber Sie haben vielleicht nicht gelesen, dass diese Messung - und viele andere Messungen von Entfernungen in der Astronomie bis hin zu ziemlich nahe beieinander liegenden Sternen - auf dem Prinzip der Parallaxe basiert, auf derselben geometrischen Tatsache, die von unseren Augen und unserem Gehirn verwendet wird, um Tiefe oder unsere Fähigkeit zu fühlen wahrzunehmen wie weit die Objekte von uns entfernt sind, indem man sie einfach betrachtet.


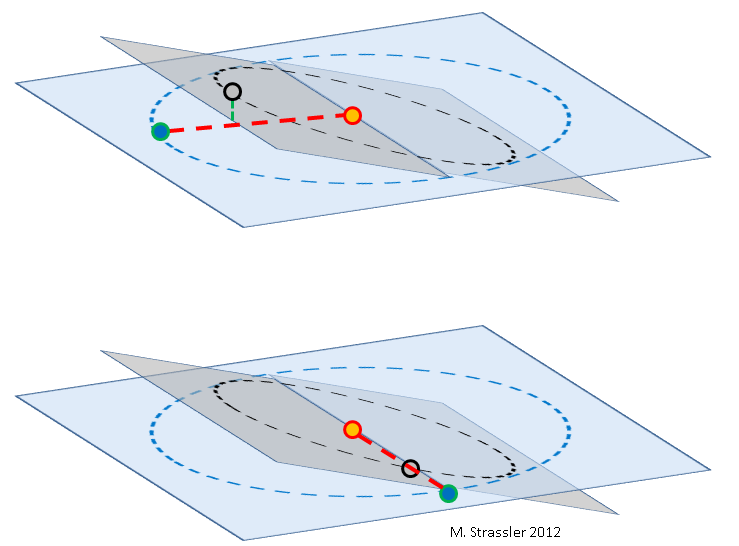Abb. 2: Erde (blau), Venus (grau) und Sonne (orange), nicht maßstabsgetreu. Die Umlaufbahn der Venus (ein schwarzer Kreis in einem grauen Rechteck) ist relativ zur Umlaufbahn der Erde (ein blauer Kreis in einem blauen Rechteck) geneigt. Der Neigungsgrad ist stark übertrieben. Da sich Erde und Venus mit unterschiedlichen Geschwindigkeiten um die Sonne drehen, können sie sich an jedem Punkt der Umlaufbahnen gegenseitig passieren.

Oben: Während dieser Passage befindet sich die Venus über oder unter (grüne Linie) der Verbindungslinie zwischen Erde und Sonne (rote Linie), sodass die Venus nicht durch die Sonnenscheibe verläuft.

Unten: In seltenen Fällen fällt die Verbindungslinie zwischen Erde und Sonne mit der Schnittlinie der Umlaufbahnebenen zusammen, und die Venus befindet sich in der Nähe derselben Linie, die zum Durchgang führt.

Ohne Parallaxe ist es auch einfach, den relativen Abstand von der Venus zur Sonne zu bestimmen, dh das Verhältnis des Radius der Umlaufbahn der Venus L _V zum Radius der Erdumlaufbahn L _E. In der Astronomie der Renaissance wurden daher die relativen Entfernungen von Planeten zur Erde und zur Sonne ziemlich früh berechnet. Um jedoch L _V und L _E getrennt zu bestimmen, ist es notwendig, die Parallaxe zu messen, und der Durchgang der Venus kann sie liefern. Der Durchgang der Venus in den 1760er Jahren ergab eine ziemlich genaue Messung von L _E - L _V , der „absoluten“ Entfernung von der Erde zur Venus; Dies ermöglichte es, L _E , L _V und die Entfernungen zu allen anderen Planeten mit einem Fehler von einigen Prozent herauszufinden. Zuvor wurde Ende des 17. Jahrhunderts die Entfernung von der Erde zum Mars gemessen, die einen Fehler von etwa 10% aufwies. Es basierte auch auf Parallaxe, aber dies ist eine ganz andere Geschichte.

Vorbemerkung: Erde und Venus und sogar die Sonne sind im Vergleich zu den Abständen zwischen ihnen sehr klein, so dass es fast unmöglich ist, genaue Bilder zu zeichnen. In Abbildungen müssen Sie immer Planeten zeichnen, die in Bezug auf die Abstände zwischen ihnen tatsächlich größer sind als sie tatsächlich sind, damit Sie das Konzept verstehen können. Denken Sie daran! Alle meine Illustrationen sind nicht maßstabsgetreu gezeichnet.

Die relativen Größen der Umlaufbahnen von Venus und Erde

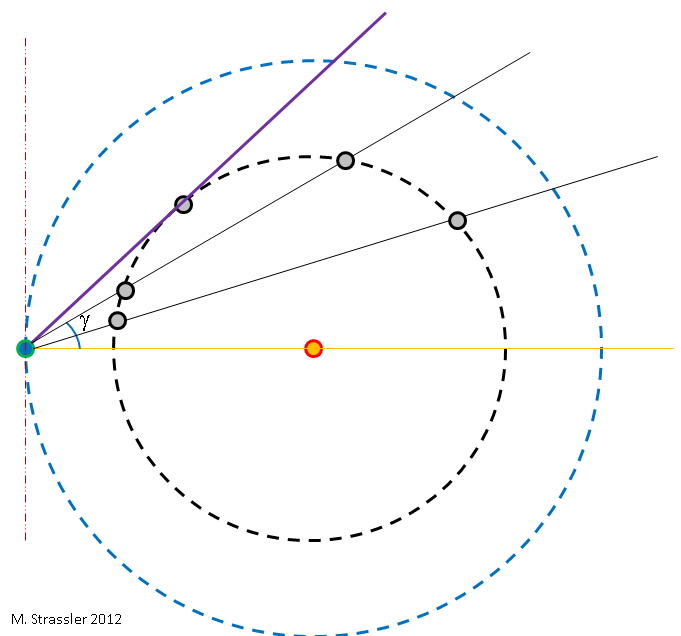Abb. 3

Um den Hauptgrund für die Einfachheit der Bestimmung von L _V / L _E zu verstehen, nehmen wir an, dass die Umlaufbahnen von Erde und Venus kreisförmig und ausgerichtet sind - sie liegen in derselben Ebene (wie in Abb. 1 gezeigt, isometrisch und in Abb. 3 eine Draufsicht). Tatsächlich sind die Umlaufbahnen der Erde und der Venus leicht verlängert und nicht ausgerichtet (Abb. 2). Aber Elliptizität und Nichtübereinstimmung von Flugzeugen sind für unsere Überlegungen nicht sehr wichtig. Deshalb können wir sie zuerst ignorieren und uns dann erneut daran erinnern, genauere Antworten zu erhalten.

Hier wenden wir die für die Physik klassische Technologie an: Wir werden eine für die aktuelle Aufgabe ausreichende Annäherung vornehmen und nicht tiefer als nötig gehen. Dies ist eine sehr wirkungsvolle Art, über Wissenschaft und Wissen im Allgemeinen nachzudenken. Es reicht aus, jede Frage mit einer bestimmten Genauigkeit zu beantworten, damit Sie die einfachste Technik verwenden können, die Ihnen die gewünschte Genauigkeit bietet. Diese Methode wird seit Jahrhunderten perfekt angewendet und ist nicht nur auf die Physik anwendbar.

Daher nehmen wir die Näherung, in der die Umlaufbahnen kreisförmig und ausgerichtet sind, und erhalten ungefähr die richtigen Antworten mit einem Fehler von einigen Prozent. Dies wird ausreichen, um die Grundkonzepte zu demonstrieren, die ich suche. Glauben Sie mir, Sie können viel genauere Berechnungen durchführen - oder Sie können selbst Experte in dieser Angelegenheit werden. Unsere Annäherung liefert jedoch nicht nur eine sehr gute Antwort, sondern kann auch zeigen, warum es so einfach ist, das Verhältnis von L _V zu L _E zu berechnen, nicht jedoch die Werte von L _V und L _E selbst.

Während des Jahres, in dem sich Erde und Venus mit unterschiedlichen Geschwindigkeiten um die Sonne drehen, ändert sich die relative Position von Erde und Venus in Bezug auf die Sonne. Wenn ich mich an einem bestimmten Tag (Tag, Monat, Jahr) entscheide, ein Bild mit der Sonne in der Mitte und der Erde links zu zeichnen, wie in Abb. 2, dann kann Venus überall in ihrer Umlaufbahn sein. Dies bedeutet, dass sich aus Sicht der Erde der Winkel zwischen Venus und Sonne am Himmel je nach Datum ändert. Dies ist in Abb. 2 dargestellt. 3, wobei der Winkel γ genannt wird. Der Winkel ist leicht zu messen; Finden Sie die Venus am Himmel nach Sonnenuntergang oder vor Sonnenaufgang und messen Sie den Winkel zwischen Venus und Sonne. siehe Bild 4.


Abb. 4

Aus Abb. Abbildung 3 zeigt, dass γ eine maximale Größe hat - den Winkel zwischen der orangefarbenen und der violetten Linie. Wenn sich die Venus im Orbit bewegt, erscheint sie bei jedem Sonnenuntergang an einer anderen Stelle. für einige Zeit wird es mehrere Nächte hintereinander höher über den Horizont steigen und dann allmählich darunter erscheinen. Wenn wir die Venus mehrere Nächte hintereinander beobachten und γ messen, können wir den Maximalwert von γ bestimmen, den ich γ _max nennen werde.

Aus Abb. In 3 ist es offensichtlich, dass (wie in 4 gezeigt) & ggr; _max kleiner als 90 ° ist, da die violette Linie senkrecht zwischen Orange und Rot liegen sollte. Geometrisch ist dies eine Folge der Tatsache, dass die Venus immer näher an der Sonne als an der Erde ist. Diese Winkel erklären, warum die Venus immer entweder unmittelbar nach Sonnenuntergang oder vor Sonnenaufgang sichtbar ist (außer an den Tagen, an denen sie sich hinter der Sonne befindet). Die Venus kann nach Einbruch der Dunkelheit nicht auf ihrem Höhepunkt sein, da sie sich dafür links von der roten Linie befinden müsste.


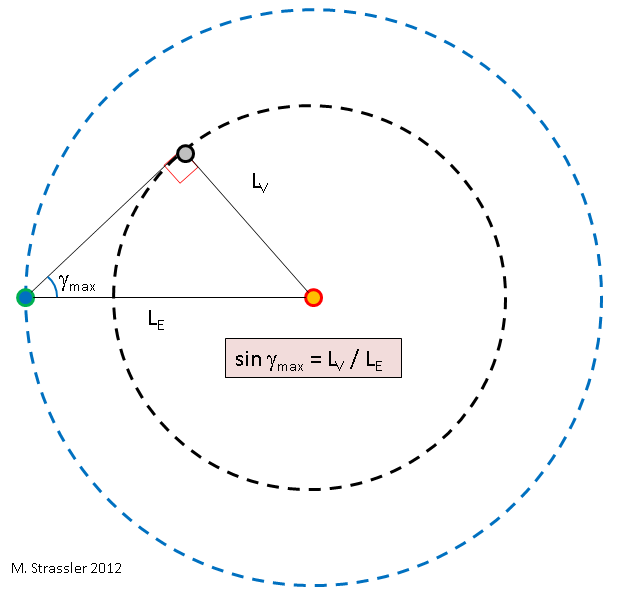Abb. 5

Nun können wir das Verhältnis der Radien zweier Bahnen - L _V zu L _E - mit γ _max bestimmen. Dies ist die einfachste Geometrie, siehe Abb. 5. Unter dem Strich ist die Linie zwischen Sonne und Venus senkrecht zur Linie zwischen Erde und Venus, wenn sich die Venus im maximalen Winkel von der Sonne befindet. Die Linien, die diese drei Objekte verbinden, bilden also ein rechtwinkliges Dreieck. Ab hier verwenden wir die Standardtrigonometrie:

$$

$$L_V / L_E = \ gamma_ {max}$$

Und von hier aus erhalten wir mit Hilfe anderer einfacher geometrischer Formeln die Beziehung zwischen den Entfernungen zu anderen Planeten.

Dies ist aus den eingangs genannten Gründen nicht ganz richtig; Die Umlaufbahnen der Planeten sind Ellipsen und liegen nicht auf der Wasserfläche. Mit anderen Worten, L _V und L _{E werden} während des Jahres nicht gespeichert, und γ _max wird in drei Dimensionen etwas komplizierter angewendet, wie in Fig. 1 dargestellt. 2, aber nicht in zwei, wie in Fig. 1, 3 und 5. Mit Hilfe genauer Messungen der Position von Venus und Sonne am Himmel ist es jedoch möglich, die genauen Umlaufbahnen von Venus und Erde um die Sonne zu bestimmen und die Berechnungen zu verbessern. Die Bedeutung ist die gleiche; Alle Messungen der Position von Venus und Sonne am Himmel erlauben es uns nur, die relativen Größen der Umlaufbahnen von Venus und Erde zu messen. Die genauen Werte von L _V und L _E können jedoch nicht auf diese Weise bestimmt werden. Hier brauchen wir einen anderen Ansatz.

Passage der Venus, Parallaxe und Entfernung zur Sonne

Der Grund, warum der Durchgang der Venus es Ihnen ermöglicht, die absoluten Werte der Umlaufbahnen von Erde und Venus zu messen, besteht darin, dass dieser Prozess von verschiedenen Orten auf dem Globus aus mit hoher Genauigkeit beobachtet werden kann, wodurch Sie zwei Perspektiven des sichtbaren Standorts der Venus relativ zur Sonne haben, gemessen von verschiedenen Orten mit Abstand zwischen ihnen. Durch Messen der Parallaxe können Sie den absoluten Wert der Entfernung von der Erde zur Venus aus dem Parallaxenwinkel und der Entfernung zwischen zwei Messpunkten auf der Erde bestimmen - genau wie bei einem anderen Objekttyp für das linke und das rechte Auge kann unser Gehirn ein Gefühl für die Tiefe vermitteln - ein Gefühl für die Entfernung von Objekten.


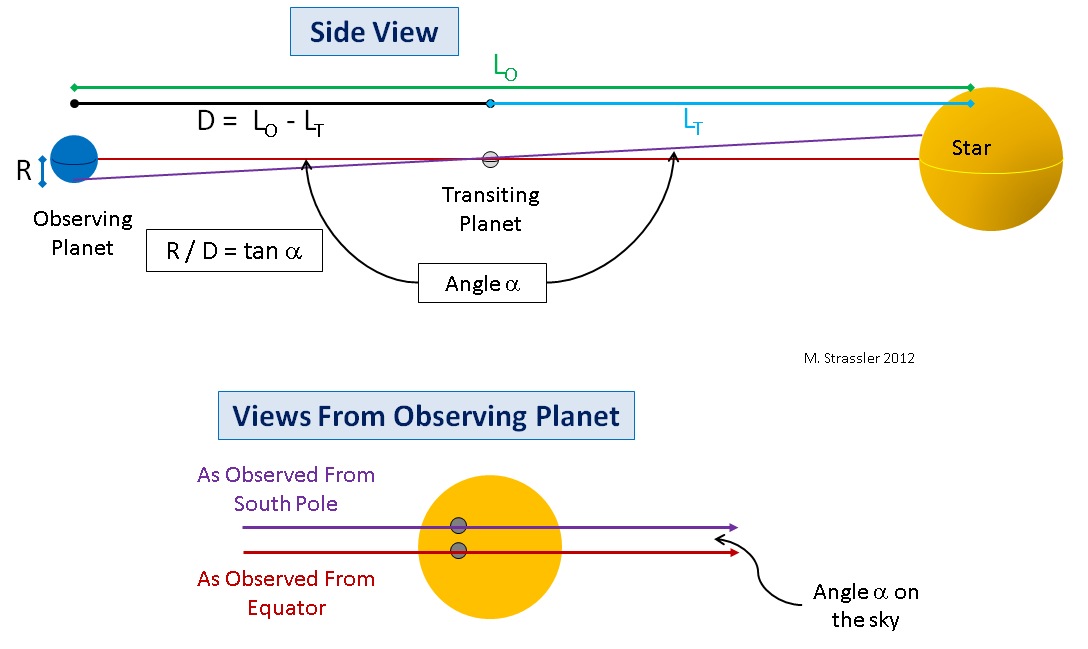Abb. 6

Lassen Sie mich für eine Demonstration zeichnen, wie es von einem großen Planeten aussehen wird. In Abb. Abbildung 6 zeigt den Planeten, mit dem wir den Durchgang beobachten (es wird die Erde sein) und den Planeten, der vor dem Stern vorbeizieht (es wird die Venus sein). Ich werde eine vereinfachte Situation vorstellen (nur um die Geometrie zu vereinfachen und das Hauptkonzept leichter zu erkennen), in der die Planeten und der Stern ausgerichtet sind, sodass aus Sicht des Beobachters am Äquator ein vorbeiziehender Planet entlang des Äquators des Sterns verläuft. Oben in Abb. Fig. 6 eine Seitenansicht zeigt; Beachten Sie die rote Linie vom Äquator des beobachtenden Planeten zum Stern durch den Äquator des Planeten, der durch die Sternscheibe verläuft.

Bei perfekter Ausrichtung sieht der Beobachter am Äquator des äußeren Planeten, wie der innere Planet am Äquator des Sterns vorbeizieht. Dies ist als rote Linie am unteren Rand von Abb. 1 dargestellt. 6. Der Beobachter vom Südpol des äußeren Planeten wird jedoch sehen, wie der innere Planet den Stern entlang des Pfades (violette Linie) nördlich des Sternäquators passiert (im Fall des Nordpols ist alles umgekehrt). Wenn wir den Winkel α am Himmel zwischen den Pfaden messen, auf denen sich ein vorbeiziehender Planet bewegt, und den Radius R des beobachtenden Planeten kennen, können wir ein rechtwinkliges Dreieck zeichnen, das den vorbeiziehenden Planeten, das Zentrum des beobachtenden Planeten und den Pol des beobachtenden Planeten mit einem kleinen Winkel verbindet. Einfache Trigonometrie gibt uns den Abstand D zwischen den Planeten während der Passage, wo

$$

$$D = R / tan \; \ alpha$$

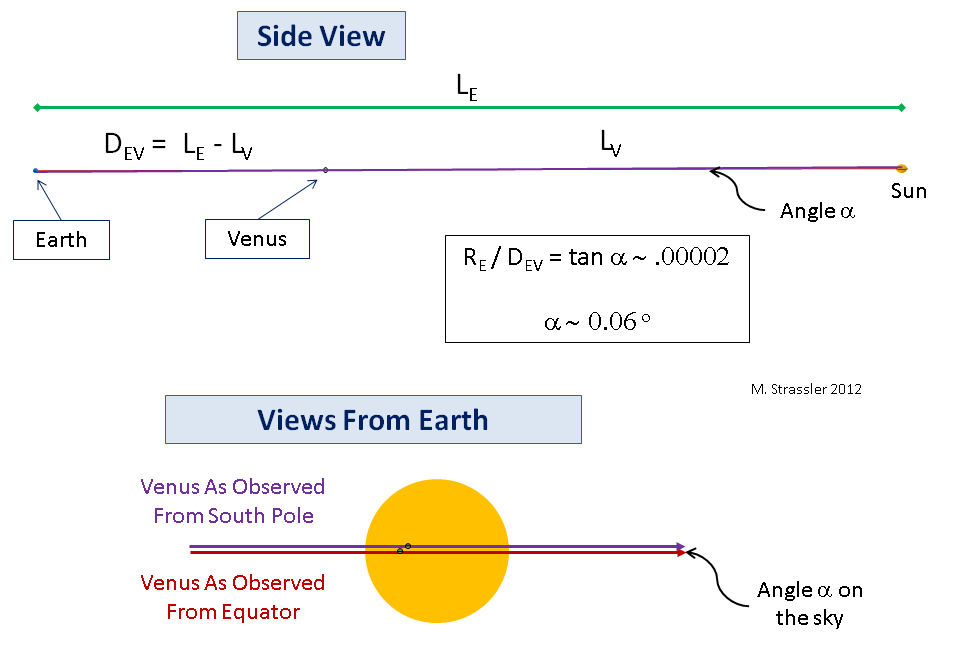Abb. 7

Gleiches gilt für die Erde, die Venus und die Sonne, außer dass die Erde und die Venus im Vergleich zum Abstand zwischen ihnen und der Sonne so klein sind, dass der Winkel α etwa 1/20 ° beträgt! (Dies ist eine ziemlich kleine Größe, aber ziemlich messbar, obwohl eine genaue Messung der Entfernung zur Sonne, die die Astronomen des 18. Jahrhunderts erhalten wollten, eine ziemlich komplizierte technisch genaue Messung der Größe eines kleinen Winkels erfordern würde). Ich werde keinen so kleinen Winkel zeichnen, also müssen Sie mein Wort dafür nehmen, dass das, was passiert, eine Version dessen ist, was ich in Abb. 2 dargestellt habe. 6, mit Planeten und einem Stern (der Sonne), der in Bezug auf Entfernungen viel kleiner als dort gemalt ist. Sogar das Bild in Abb. 7 macht Planeten viel größer als sie sind. Die Idee bleibt jedoch unverändert: Der Abstand D _EV zwischen der Erde und der Venus während des Durchgangs kann durch Messen des Parallaxenwinkels α bestimmt werden (unten in Abb. 7; beachten Sie, dass der Winkeldurchmesser der Sonne etwa 1/2 ° beträgt).

Es gibt jedoch noch viele Fragen:

• Ich erzählte, wie man D _EV misst, die Entfernung von der Erde zur Venus während der Passage. Aber war es nicht unser Ziel, L _E und L _V zu messen, die Entfernung von der Erde zur Sonne und von der Venus zur Sonne?
• Niemand ging zum Südpol der Erde, um den Durchgang der Venus 1761 oder 1769 zu beobachten.
• Ich nahm perfekt ausgerichtete Umlaufbahnen der Erde, der Venus und der Position der Sonne an, so dass man von einem Punkt am Äquator der Erde aus sehen konnte, wie sich die Venus entlang des Äquators der Sonne bewegte. Dies ist jedoch tatsächlich nicht der Fall und sieht nicht einmal wie eine typische Komplettlösung aus (und 2012 war dies auch nicht der Fall).
• Der Winkel α ist klein genug, um genau gemessen zu werden - insbesondere in den Tagen vor dem Fotografieren und Instant Messaging, da keine eindeutigen Angaben zum Standort des Nordpols der Sonne vorliegen, was es schwierig macht, die Messungen des Venuspfades von zwei verschiedenen Punkten auf der Erde aus genau zu vergleichen. Das primäre Ziel war jedoch, den Winkel nicht schlechter als 1 Teil von 500 (0,2%) zu messen (obwohl das Ergebnis aufgrund des Schwarztropfeneffekts näher an 1 Teil von 50 (2%) lag).

Wie gehe ich mit diesen Problemen um?

Wie gehen Sie zunächst von der Messung von D _EV zur Messung der gewünschten Werte L _E und L _{V über} ? Es ist einfach - wir kennen bereits alle Beziehungen, insbesondere L _E / L _V (ungefähr aus Abb. 4 oder, wenn wir uns dem Problem genauer nähern, können wir es genauer berechnen) aus dem maximalen Winkel γ _max zwischen Venus und Die Sonne aus der Sicht der Erde. Wir kennen auch D _EV = L _E - L _V = L _E (1 - L _V / L _E ) aus Fig. 7. Daher können wir einen ungefähren Wert von L _{E erhalten,} indem wir:

$$

$$L_E = D_ {EV} / (1 - L_V / L_E) = R / tan \; α / (1 - sin \; \ gamma_ {max})$$

Dabei ist α der während des Transits gemessene Parallaxenwinkel und γ _max der maximale Winkel zwischen Venus und Sonne (Abb. 5). Genauere Messungen erfordern eine komplexere Geometrie, jedoch mit derselben Grundidee.

Zweitens müssen zwei Dimensionen des Venuspfades nicht vom Äquator und vom Erdpol aus gemessen werden, selbst wenn die Umlaufbahnen der Planeten perfekt ausgerichtet wären. Sie können aus zwei beliebigen Breiten gemessen werden. Die Geometrie wird etwas komplizierter, aber nicht viel, aber das Prinzip bleibt bestehen (siehe Abb. 8).


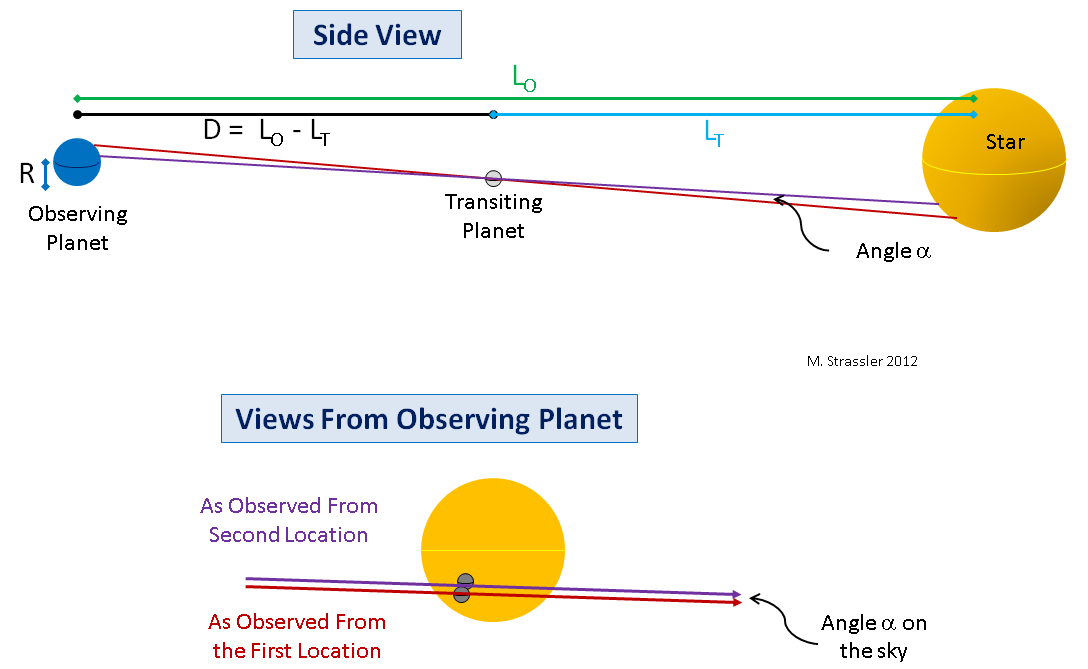Abb. 8

Drittens erscheint auch ohne perfekte Ausrichtung ein kleiner Parallaxenwinkel, wenn Werte von zwei verschiedenen Punkten der Erde gemessen werden. Wenn dieser Winkel gut gemessen wird, kann diese Messung (durch etwas komplexere Gleichungen) in D umgewandelt werden. 8, runter.

Die vierte Frage ist das historisch komplexe Problem der Messung der Winkelverschiebung des Weges der Venus beim Durchqueren des Winkels α, das uns zu einem alternativen Versuch führt, die Zeit zu messen - entweder die Laufzeit oder einfach den Beginn und das Ende der Passage und nicht die Winkel. Die erste Option wurde von Halley auf der Grundlage der Ideen von Gregory vorgeschlagen, und die zweite als weitere Verbesserung wurde von Joseph Nicola Delille vorgeschlagen . Die Halley-Methode erforderte keine Uhrensynchronisation an verschiedenen Orten der Erde. Die erforderliche Delil-Methode basierte daher auf einer fortschrittlicheren Uhrentechnologie.

Selbst im 17. oder 18. Jahrhundert ist es viel einfacher, das Intervall oder die Momente des Beginns und des Endes der Sonnenfinsternis genau zu messen, als den Ort der Venus relativ zur Sonnenscheibe genau zu messen, insbesondere ohne Fotografie. In Abb. Abbildung 9 zeigt, dass die violetten und roten Pfade der Venus, die die Sonne überqueren, leicht unterschiedlich lang sind, da sie sie nicht an einer Stelle kreuzen. Dies bedeutet, dass sich die Dauer der Passage um die mit dem Parallaxenwinkel verbundene Zeit unterscheidet. Leider stellt sich heraus, dass alles komplizierter ist, als es auf den ersten Blick aussieht - die Erde dreht sich und bewegt sich um die Sonne, so dass der Betrachter während des Durchgangs der Venus durch die Sonnenscheibe eine ziemlich beträchtliche Strecke zurücklegt. Daher ist viel Aufwand erforderlich (Berechnungen sind ziemlich kompliziert, obwohl sie mit modernen Computern viel einfacher sind), um den Unterschied in den Zeitintervallen von Beginn und Ende der Passage zu bestimmen, die von zwei verschiedenen Beobachtern auf der Erde in Abhängigkeit von der Entfernung zur Sonne beobachtet werden.

Zu Beginn des 18. Jahrhunderts verstand Halley alle notwendigen geometrischen Prinzipien (wenn Sie die veraltete englische Ausdrucksweise und den veralteten englischen Stil von seinen Texten abziehen, werden Sie überrascht sein, wie modern seine komplexen Aussagen klingen, und Sie werden sehen, dass Wissenschaftler vor dreihundert Jahren den heutigen Wissenschaftlern sehr ähnlich waren. besaß die gleiche Intelligenz und es fehlte nur die wissenschaftliche Technologie von heute).


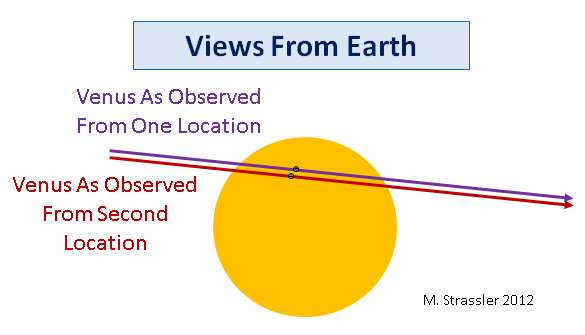Abb. 9

All dies deutet darauf hin, dass die Parallaxe - der Unterschied in der sichtbaren Position, die der Venus in Bezug auf die Sonne zugeschrieben wird, aus der Sicht von Beobachtern, die sie gleichzeitig, aber von verschiedenen Orten auf der Erde aus messen - historisch gesehen eine sehr wichtige Methode war bestimmte die Größe des Sonnensystems. Heutzutage stehen uns leistungsfähigere Methoden zur Verfügung, aber Sie könnten daran interessiert sein, dass das, was Sie heute am Himmel sehen, von großer historischer Bedeutung ist, oder Sie können einfach den Blick auf die Venus genießen, die sich majestätisch um unseren Stern bewegt.