Programmierer-Polynom- und Spline-Handbuch

Sie sind also ein Programmierer. Warum brauchen Sie überhaupt Polynome? Zum Beispiel, dass es ein guter geometrischer Ton ist, aus dem man verschiedene Dinge formen kann.

Aus unserem Artikel , der die Essenz der mathematischen Analyse am Beispiel von Python, Blut und Dynamit erklärt, geht hervor, dass Sie beliebige Funktionen als Polynome analysieren und synthetisieren können. Es ist jedoch nicht erforderlich, speziell mit Funktionen zu arbeiten. Manchmal müssen Sie möglicherweise einen Spline aus mehreren Punkten oder Eigenschaften modellieren, z. B. aus Tangenten von Kurven. Sie müssen beispielsweise eine Art Animation oder einen schönen Videoeffekt erstellen oder eine Kurve zeichnen, die durch bestimmte Punkte verläuft, oder eine Oberfläche erstellen, die an einer Stelle flach und an einer anderen gekrümmt ist.

Polynome, einschließlich Spline-Polynome, sind möglicherweise nicht immer das beste Werkzeug für diese Aufgabe, besitzen jedoch einige Funktionen, die Programmierer wirklich zu schätzen wissen. Sie sind einfach und vielseitig in der Natur und vor allem sehr effektiv in Bezug auf die Leistung. Nehmen Sie zum Beispiel das folgende Polynom:



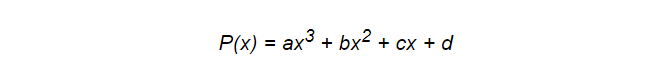
Zur Berechnung sind nur 6 Multiplikationsaktionen und 3 Additionen erforderlich. Dies ist wichtig, da Ihr Modell ständig berechnet wird. Aber hier können wir eine Optimierung durchführen. Horners Schema wird uns dabei helfen. Mit seiner Hilfe kann das gleiche Polynom geschrieben werden wie



Und das sind nur 3 Multiplikationen und 3 Additionen. Sie sehen, wir haben gerade erst begonnen und Sie haben bereits gelernt, ein Drittel der Berechnungen loszuwerden.

Polynominterpolation

Die Aufgabe, ein Polynom vom Grad n an n + 1 Punkte im Raum anzupassen, wird als Polynominterpolation bezeichnet. Es gibt verschiedene Möglichkeiten, dies zu implementieren. Sie können die Newton- oder Lagrange- Interpolationsformeln verwenden. Der einfachste Weg, das Interpolationspolynom zu erhalten, besteht darin, ein lineares Gleichungssystem zu lösen.

Wenn ein Polynom durch einen Punkt geht, können wir offensichtlich sagen, dass P (xi) = yi ist . Angenommen, wir möchten ein Polynom an eine Menge von drei Punkten anpassen. Dies bedeutet, dass:



Im allgemeinen Fall können wir keine Linie durch drei beliebige Punkte ziehen. Und so müssen wir es biegen und eine Parabel bilden. Oder mit anderen Worten, führen Sie ein Polynom zweiten Grades ein, das auch als quadratische Funktion bezeichnet wird.



Da xs und ys bekannt sind, müssen wir nur das System lösen und die Koeffizienten a, b, c herausfinden. Da dieses System aus drei Gleichungen und drei Variablen besteht, können wir normalerweise eine einzige Lösung erhalten.

Um dies sicherzustellen, verschieben Sie die Position der drei Punkte im unteren Diagramm und sehen Sie, was passiert.



Dieser Graph ist auch sehr nützlich für die mentale Analyse linearer Systeme. Im allgemeinen Fall ist es unmöglich, an drei Punkten eine gerade Linie anzupassen, ebenso wie es unmöglich ist, eine Lösung für ein System von n Gleichungen mit n-1 unbekannten Variablen zu finden. Aber manchmal ist es möglich. Zum Beispiel in Fällen, in denen einige der Punkte zusammenfallen oder alle absichtlich auf einer geraden Linie liegen.

Die umgekehrte Situation ist noch interessanter. Wir können eine unendliche Anzahl von Parabeln durch zwei gegebene Punkte ziehen. Alle von ihnen eignen sich gleichermaßen als Lösung für das Problem. Gleichzeitig können wir keine einzigartig bessere Lösung für Systeme mit n Gleichungen und n + 1 Variablen finden.

Aber was ist, wenn es noch möglich ist? Was ist, wenn wir ein zusätzliches Kriterium für die Auswahl der am besten geeigneten Option einführen können?

Synthese

Ähnliche Fragen führen uns zum Gebiet der Polynomsynthese. In unserem Fall ist dies eine Kreuzung zwischen Polynomreihen und Polynominterpolation. Mit Hilfe von Reihen können wir irgendwann eine Funktion basierend auf ihren Ableitungen modellieren, und mit Hilfe der Synthese können wir sowohl Punkte als auch Ableitungen verwenden (und nicht nur diese, sondern ein anderes Mal mehr dazu).

Die Ableitung einer Funktion hängt eng mit den geometrischen Eigenschaften ihres Graphen zusammen. Die erste Ableitung bestimmt die Tangente der Steigung der Tangente und die zweite die Krümmung.

Angenommen, wir müssen eine Funktion definieren, die durch zwei Punkte verläuft und deren Tangente an beiden Punkten kennt. In diesem Fall können wir es leicht als Polynom synthetisieren.

Nach wie vor müssen wir ein Gleichungssystem aufschreiben. Jetzt brauchen wir vier Bedingungen, also sollten wir ein Polynom vom Grad 3 wählen, dh eine kubische Funktion.



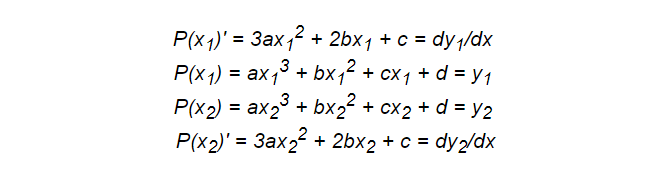
Einige der Gleichungen basieren auf Punkten, während andere Ableitungen sind. Hier können auch Integrale hinzugefügt werden, um die erforderlichen ganzzahligen Eigenschaften einzuführen, was diese Technik sehr effektiv macht.

Wir werden jedoch weiterhin eine Funktion betrachten, die zwei Punkte einer durchgehenden glatten Linie mit tangentialen Einschränkungen an diesen Punkten verbindet.

Runge-Phänomen

Die Polynominterpolation hat eine unangenehme Eigenschaft, die sich in einer Zunahme des Wachstums von Schwingungen an beiden Enden des Intervalls mit einer Zunahme der Anzahl von Punkten äußert. Dieses Phänomen wird als Runge-Phänomen bezeichnet. Dies schränkt die Möglichkeit der Verwendung einfacher Polynominterpolationen ein.

Ein weiterer Nachteil dieses Ansatzes ist seine globale Natur, dh eine Änderung der gesamten Funktion zusammen mit der geringsten Änderung der Position von mindestens einem Punkt. In Kombination mit Schwingungen ist das Ergebnis Chaos.

Chebyshev-Knoten

Eine Möglichkeit, das Chaos zu bekämpfen, besteht darin, ein spezielles Netz für die Interpolation auszuwählen - Chebyshev-Knoten . Dies sind spezielle x-Werte, die erhalten werden, indem ein Halbkreis mit einem Radius von 1 in gleiche Fragmente geteilt und auf die x-Achse projiziert wird.

Im Allgemeinen ist eine bestimmte mathematische Magie in dieser Technik verborgen, aber aus pragmatischer Sicht soll das Runge-Phänomen minimiert werden. Und obwohl es nicht möglich ist, die Interpolation vollständig vorhersehbar zu machen, funktioniert alles stabil im Intervall (-1: 1).



Natürlich können Sie das Intervall entlang der X-Achse beliebig verlängern, indem Sie die eindimensionale affine Transformation verwenden. Es ist nicht erforderlich, das Segment (-1; 1) einzuhalten .

Gleichzeitig behält die Interpolation ihre Allgegenwart. Das Ändern des ersten Punkts wirkt sich immer noch auf den Betrieb der Funktion in der Nähe des letzten aus, wenn auch nicht so stark.

Splines

Es gibt einige Arten von Splines, aber alle sind durch ein Anwendungsszenario vereint. Sobald die globale Interpolation aus irgendeinem Grund nicht mehr für unsere Aufgaben geeignet ist, können wir unser Intervall in kleinere Fragmente aufteilen und einzelne Funktionen für die Interpolation für jedes dieser Fragmente definieren.

Das einzige, was wir berücksichtigen müssen, ist die Notwendigkeit, sie an den Enden zu verbinden, um die Kontinuität aufrechtzuerhalten. Wenn wir die Kontinuität nicht nur der endgültigen, stückweise definierten Funktion, sondern auch ihrer ersten Ableitung garantieren, stimmen in diesem Fall die Tangenten der einzelnen Segmente überein und der Zeitplan sieht glatt aus.

Es gibt eine bestimmte Klassifizierung von Splines. Nehmen Sie zum Beispiel einen Polynom-Spline, der aus zwei Fragmenten besteht. Wenn jedes Fragment davon durch ein Polynom dritten Grades bestimmt wird, heißt es kubisch. Es kann beispielsweise eine solche Eigenschaft wie die Kontinuität der ersten Ableitung besitzen, da die Tangenten an der Verbindungsstelle der Fragmente zusammenfallen. Seine Fragmente sind nicht gleich breit. Es ist nicht natürlichen Ursprungs, da wir Derivate an seinen Enden kontrollieren können. Und natürlich ist dies ein Interpolations-Spline, da er genau durch die von uns angegebenen Gitterpunkte verläuft.

Fazit

Die Wahrscheinlichkeit, dass Sie jemals Ihre eigene Interpolation in die Praxis umsetzen müssen, ist äußerst gering. Es gibt viele vorgefertigte Lösungen, und in den meisten Fällen müssen Sie nur das richtige Werkzeug für den Job auswählen. Dieser Wissensbereich ist nicht so kompliziert, aber die Anzahl unbekannter Wörter und Namen kann sich verdrängen.

Der Zweck dieses Handbuchs war es, Ihnen ein grundlegendes Verständnis der Ideen zu vermitteln, die für die Arbeit mit Polynomen und Splines verwendet werden. In keinem Fall gibt er vor, vollständig zu sein, denn tatsächlich sind ganze Bücher über jedes der kleinen Kapitel dieses Materials geschrieben. Wir hoffen jedoch zumindest, dass der interaktive Ansatz zur Präsentation in diesem Material nicht nur für eine kurze Einführung nützlich ist, sondern Ihnen bei Bedarf hilft, fortgeschrittenere Themen zu meistern.