Kosmologie - Stanford. Zusammenfassung. Vorlesung 1

Dieser Artikel eröffnet eine Reihe von Vorlesungsskripten zur Kosmologie der Stanford University. Die Vorlesungen selbst in englischer Sprache sind erhältlich bei: Cosmology (2013) - Leonard Susskind - Stanford University . Ich habe mir die Videovorlesung angesehen und mit Vergnügen skizziert. Dozent Leonard Susskind erklärt sehr zugänglich und macht Spaß. Es ist offensichtlich, dass er ein talentierter Mensch und ein ausgezeichneter Lehrer ist.

Die Stanford University ist auch dafür bekannt, dass unser herausragender Landsmann Andrei Linde dort arbeitet, der wahrscheinlich bald den Nobelpreis für Physik für seinen Beitrag zur modernen Kosmologie erhalten wird. Wen kümmert es, ich rate Ihnen, seinen öffentlichen Vortrag Die vielen Gesichter des Universums zu sehen .

Diese Zusammenfassung ist mein Versuch der Selbstbildung. Ich würde es immer noch für mich in ein Notizbuch schreiben. Aber ich habe beschlossen, Geschäft mit Vergnügen zu verbinden. Ich hoffe, dass es auch für jemanden interessant sein wird.

Machen Sie sofort eine Reservierung, dass ich versucht habe, Notizen in der Nähe des Originaltextes zu machen. An einigen Stellen erlaubte ich mir jedoch, die Aussagen des Dozenten aufgrund meiner eigenen Erfahrung als Fachphysiker zu ergänzen oder zu verallgemeinern. Dies geschah ausschließlich, um das Verständnis, das Verständnis und die Assimilation des Materials zu erleichtern.

In diesem Artikel wird Ihnen eine Zusammenfassung von Vorlesung 1 angeboten. Vielleicht erscheint später eine Fortsetzung.

Historischer Rückblick

Kosmologie ist ein sehr altes Thema. Die Geschichte der Kosmologie reicht Jahrtausende zurück. Insbesondere die alten Griechen kannten sich sehr lange mit Kosmologie aus.

Diese Vorträge decken den Zeitraum ab, der nicht weiter als bis zur zweiten Hälfte des 20. Jahrhunderts reicht, als Edwin Hubble das Gesetz der Expansion des Universums entdeckte.

Wenn wir über Kosmologie als Wissenschaft sprechen, dann ist dies ein ziemlich neues Wissensgebiet. Die moderne Kosmologie geht auf die Entdeckung der Mikrowellenreliktstrahlung und die Formulierung der Urknalltheorie zurück . Und das geschah erst in den 1960er Jahren.

Bis zu diesem Zeitpunkt war die Kosmologie kein Zweig der Physik, sondern gehörte zu den Naturwissenschaften. Das heißt, in der Kosmologie setzte sich der phänomenologische Ansatz durch: Beobachtung, Messung, Klassifizierung, Katalogisierung usw.

Zu diesem Zeitpunkt war die Genauigkeit der Messungen gering. Und deshalb war es unmöglich, genaue Aussagen zu formulieren. Es gab Gleichungen, aber sie waren falsch und ungenau. Physiker waren schon immer in den Untersuchungsprozess involviert, da Sterne, Galaxien und andere Himmelskörper physikalische Eigenschaften wie zum Beispiel Drehimpuls besitzen. Physikalische Chemiker waren ebenfalls beteiligt, da Himmelskörper eine chemische Zusammensetzung haben.

Die Einstellung zum Universum selbst als physikalischem Objekt, das Universum als System, das mathematisch unter Verwendung einer Reihe physikalischer Prinzipien und der entsprechenden exakt korrekten Gleichungen untersucht werden sollte - dies ist ein relativ junger Ansatz.

Eigenschaften des Universums

In diesen Vorlesungen wird das Universum als physikalisches System betrachtet. Und wir werden es mit Gleichungen untersuchen. Wir können unsere Erforschung des Universums mit einigen allgemeinen Beobachtungen beginnen.

Isotropie

Die erste Beobachtung, die im Allgemeinen möglicherweise nicht absolut genau ist, genau wie die gesamte Physik nicht absolut genau ist, ist, dass das Universum isotrop ist .

Isotropie bedeutet, dass das Universum in jeder Richtung gleich aussieht. Dies gilt natürlich nur für ausreichend große Entfernungen. Wenn Sie zu genau hinschauen, kann es sein, dass aufgrund lokaler Inhomogenitäten, beispielsweise aufgrund der Form unserer Galaxie, keine Isotropie beobachtet wird.

Einheitlichkeit

Wenn das Universum isotrop ist, kann mit großer Sicherheit argumentiert werden, dass das Universum auch homogen sein muss . Homogenität bedeutet nicht Einheitlichkeit in jede Richtung, sondern an jedem Ort. Das heißt, im großen Maßstab sieht das Universum gleich aus, unabhängig davon, wo sich der Beobachter befindet - in unserer Galaxie oder in einer anderen, die weit, weit von uns entfernt ist.

Galaxien

Galaxien auf der Skala des Universums sind effektiv Massenkonzentrationspunkte . Wir können sie als materielle Punkte behandeln. Die ungefähre Anzahl von Galaxien im sichtbaren Teil des Universums beträgt einhundert Milliarden $$$10 ^ {11} = 100 \, 000 \, 000 \, $ 00$ . Jede Galaxie enthält wiederum ungefähr $$$10 ^ {11}$ hundert Milliarden Sterne. Wir müssen uns daran erinnern, dass dies die Anzahl der Galaxien nur innerhalb der Kugel ist, die wir sehen können. Nur soweit Astronomen mit Teleskopen sehen können. Das heißt, das weiteste, was wir sehen können, befindet sich in einer Entfernung von der Stelle, an der das Licht uns während der gesamten Existenz des Universums erreicht hat: ungefähr 13 Milliarden Jahre.

Eine interessante Tatsache. Die Gesamtzahl der Sterne im sichtbaren Teil des Universums $$$10 ^ {11} \ cdot 10 ^ {11} = 10 ^ {22}$ und wenn jeder Stern durchschnittlich 10 Planeten hat, dann stellt sich heraus $$$10 ^ {23}$ - die Anzahl der Avogadro-Planeten im Universum. Planetarischer Mol Substanz! (Dozent lacht)

Ein Argument gegen die Homogenität des Universums. Gegenargument

Betrachten Sie ein Stück des Universums, in dem wir uns befinden. Wir wissen es mit Sicherheit, weil wir sehen, dass das Universum isotrop ist . Wir nehmen an, dass das Universum auch homogen ist . Aber was würde passieren, wenn das Universum nicht homogen wäre?

Wenn das Universum isotrop ist, besteht die einzige Möglichkeit, nicht homogen zu sein, darin, eine Struktur in Form einer Art Schale zu haben.


Die Hypothese eines heterogenen Universums. Links ist ein isotropes homogenes Universum, rechts ein isotropes, nicht homogenes Universum. Das Kreuz in der Mitte kennzeichnet uns.

Wenn dies so wäre, würde das Universum an keinem anderen Punkt isotrop aussehen. Das heißt, wenn wir nicht glauben wollen, dass wir uns irgendwie genau im Zentrum des Universums befanden und das gesamte Universum eine sphärische Symmetrie um uns herum hat, müssen wir zugeben, dass das Universum nicht nur isotrop, sondern auch homogen ist.

Kosmologisches Prinzip

Wenn wir also nicht glauben, dass wir uns genau im Zentrum des Universums befinden, muss das Universum homogen sein. Ein homogenes Universum bedeutet, dass das Universum im gesamten Volumen gleichmäßig mit Partikeln (Galaxien) gefüllt ist. Dies nennt man das kosmologische Prinzip . Das kosmologische Prinzip ist wahr, weil unsere Beobachtungen dies natürlich bis zu einem gewissen Grad anzeigen.

Einige Astronomen behaupten, sie hätten große Heterogenitäten im Universum beobachtet. Der Vortragende bezweifelt die Zuverlässigkeit dieser Quellen und Aussagen.

Natürlich ist die Vorstellung von der Homogenität des Universums nicht absolut zutreffend. Sogar die Tatsache, dass Galaxien existieren, deutet bereits auf Heterogenitäten hin. Übrigens gibt es nicht nur Galaxien, sondern auch Galaxienhaufen. In ziemlich großem Maßstab, ungefähr in der Größenordnung von 1 Milliarde Lichtjahren, sieht das Universum jedoch homogen aus.

Das kosmologische Prinzip war zunächst nur ein Postulat. Mit der Anhäufung von Beobachtungsdaten wurde dies jedoch immer zuverlässiger bestätigt, und am Ende wurde Reliktmikrowellenstrahlung entdeckt, was darauf hinweist, dass die anfängliche Verteilung der Materie im Universum sehr homogen war.

Erklärung des körperlichen Problems

Es gibt ein gleichmäßiges Gas aus galaktischen Partikeln. Und jede Galaxie interagiert mit anderen Galaxien. Galaxien sind insgesamt elektrisch neutral. Aber sie sind gravitativ nicht neutral. Sie interagieren durch die Newtonsche Schwerkraft. Und dies ist die einzige wichtige Kraft im großen Maßstab. Die Schwerkraft wirkt auf Galaxien und versucht, sie alle zusammen zu ziehen.

Wenn Sie sich also einen Punkt im Universum ansehen und sich fragen, wohin er sich bewegen soll, können Sie davon ausgehen, dass er von allen Seiten von der gleichen Menge an Masse umgeben ist. Nach dieser Logik kann davon ausgegangen werden, dass sich überhaupt keine Galaxie bewegen sollte und das Universum statisch sein sollte, da das Ergebnis von Kräften, die auf einen beliebigen Punkt im Universum wirken, Null ist. Das ist absolut falsch!

Und jetzt erhalten wir Newtonsche Bewegungsgleichungen für das Universum. Man konnte hören, dass das expandierende Universum gut mit Einsteins allgemeiner Relativitätstheorie übereinstimmt und dass das Gesetz des expandierenden Universums vor der allgemeinen Relativitätstheorie unverständlich war. Das ist einfach nicht wahr. Vielleicht war das so historisch. Dies ist jedoch nur eine historische Tatsache über Daten, nicht über Logik. Newton könnte die Gleichungen eines expandierenden Universums erhalten. Und jetzt werden wir es so machen, wie Newton es hätte tun sollen.

Koordinatensystem

Bei jedem physikalischen Problem muss zunächst ein Koordinatensystem eingeführt werden. Anstatt den Gitterschritt als Entfernung zu wählen: 1 Meter, eine Million Kilometer, tausend Lichtjahre, werden wir ein Gitter so wählen, dass seine Knoten starr an Galaxien gebunden sind. Da das Universum homogen ist, können wir es tun. Dann bleiben die Galaxien immer ungefähr auf den gleichen Koordinaten, unabhängig davon, was mit dem Universum passiert. Das heißt, Galaxien scheinen im Koordinatengitter „eingefroren“ zu sein.

Es ist überhaupt nicht offensichtlich, dass dies möglich ist. Wenn sich die Galaxien völlig zufällig und in völlig andere Richtungen bewegten, konnten wir dies nicht tun. Aber wir sehen, dass sich Galaxien zufällig bewegen. Wir sehen, dass sich die Galaxien gemeinsam bewegen, genau so, als wären sie in ein bestimmtes Koordinatengitter eingebettet. Und was wir sehen, ermöglicht es uns, dies zu tun, da die Geschwindigkeiten der Galaxien relativ zueinander konstant und nicht zufällig sind.

Wir führen ein Raster ein $$$(x, y, z)$ . Diese Koordinaten werden nicht in Längeneinheiten gemessen. Betrachten wir zwei durch ein Intervall getrennte Galaxien $$$\ Delta x$ dann die Entfernung $$$D$ zwischen ihnen (in Metern) wird ausgedrückt als

$$

$$D = a \, \ Delta x$$

wo $$$a$ Ist ein Skalenparameter, der eine Konstante sein kann, aber im Allgemeinen nicht sein kann. Der Skalierungsparameter kann zeitabhängig sein. $$$a = a (t)$ .

Nach dem Satz von Pythagoras wird der Abstand zwischen zwei Galaxien im Allgemeinen wie folgt geschrieben:

$$

$$D = a (t) \ sqrt {\ Delta x ^ 2 + \ Delta y ^ 2 + \ Delta z ^ 2}$$

Und natürlich der Parameter $$$a$ ist keine Konstante. Wenn es eine Konstante wäre, wären die Galaxien statisch und würden sich nirgendwo bewegen. Und das beobachten wir nicht. Wir sehen, dass sie auseinander fliegen.

Hubble-Gesetz

Wir schreiben die Relativgeschwindigkeit zwischen zwei Galaxien. Wir unterscheiden die vorherige Formel zeitlich. Wir berücksichtigen das $$$\ Delta x$ - Dies ist ein festes Intervall, das nicht gemäß den Bedingungen für die Erstellung eines Koordinatensystems geändert werden kann. Dann

$$

$$\ mathcal {V} = \ dot {a} \, \ Delta x$$

wo wir die Notation verwenden $$$\ dot {a} = da / dt$ .

Wir schreiben nun das Verhältnis der Relativgeschwindigkeit zweier Galaxien zum Abstand zwischen ihnen

$$

$$\ frac {\ mathcal {V}} {D} = \ frac {\ dot {a} (t)} {a (t)}$$

Beachten Sie das $$$\ Delta x$ wird reduziert, und dieses Verhältnis hängt überhaupt nicht von den Koordinaten ab. Das heißt, diese Formel gilt für zwei beliebige Galaxien, egal wie weit oder nahe sie sind.

Diese Beziehung wird als Hubble- Konstantenparameter bezeichnet .

$$

$$H (t) = \ frac {\ dot {a} (t)} {a (t)}$$

und es hängt nicht von den Koordinaten ab. Dann können Sie dasselbe in Standardform schreiben

$$

$$\ mathcal {V} = H \, D$$

Die relative Geschwindigkeit zweier Galaxien ist proportional zum Abstand zwischen ihnen.

Sie müssen verstehen, dass wir es niemals aufgeschrieben hätten, wenn Hubble sein Gesetz nicht entdeckt hätte. Hubbles Gesetz ist dagegen nicht so überraschend. Es gibt ein Sprichwort: "Es ist nicht überraschend, dass das schnellste Pferd vor allen reitet." Je schneller Sie sich bewegen, desto weiter sind Sie. Und das ist eine Tatsache, die Hubble entdeckt hat.

Masse der Materie im Universum

Betrachten Sie etwas Volumen $$$\ Delta x \, \ Delta y \, \ Delta z$ . Wir stellen eine Frage: Welche Masse ist in diesem Band konzentriert? Lass $$$\ nu$ Ist die Masse einer Substanz in einem Elementarvolumen $$$dx \, dy \, dz$ (in Kilogramm). Dann die Masse im Volumen $$$\ Delta x \, \ Delta y \, \ Delta z$ ist gleich

$$

$$M = \ nu \, \ Delta x \, \ Delta y \, \ Delta z$$

Was ist das metrische Volumen dieses Bereichs? Als $$$D = a \, \ Delta x$ wir können schreiben

$$

$$V = a ^ 3 \, \ Delta x \, \ Delta y \, \ Delta z$$

Wie dicht ist der Stoff in diesem Bereich? Per Definition ist die Dichte $$$\ rho = M / V$ unter Berücksichtigung der beiden vorhergehenden Formeln erhalten wir

$$

$$\ rho = \ frac {\ nu} {a ^ 3}$$

Dies ist die physikalische Standarddichte eines Stoffes.

Obwohl die Gesamtmenge der Masse im Volumen $$$\ Delta x \, \ Delta y \, \ Delta z$ ändert sich nicht, da Galaxien in das Koordinatengitter „eingefroren“ werden, kann sich die absolute Materiedichte im gleichen Volumen ändern, da der Parameter $$$a (t)$ hängt von der Zeit ab.

Newtons Theorem

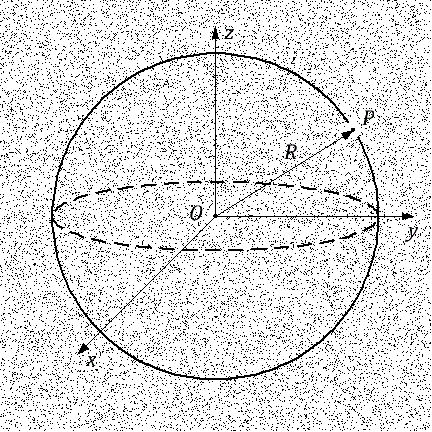Illustration zum Newtonschen Theorem

Betrachten Sie zwei Galactiti. Wir können immer einen von ihnen an den Ursprung setzen. Lass die Galaxie $$$O$ ist am Ursprung und die Galaxie $$$P$ ist in einiger Entfernung von ihr.

Newtons Theorem besagt, dass die Schwerkraft auf eine Galaxie wirkt $$$P$ hängt nur von der Menge der Masse innerhalb der Kugel ab, die am Ursprung zentriert ist $$$O$ und durch die Galaxie gehen $$$P$ . Die zweite Aussage des Newtonschen Theorems lautet, dass die gesamte Masse innerhalb dieser Kugel als im Zentrum am Ursprung am Punkt konzentriert betrachtet werden kann $$$O$ vorausgesetzt, dass die Masse innerhalb der Kugel, wenn nicht gleichmäßig, dann zumindest isotrop verteilt ist .

Mit anderen Worten, die Wirkung der gesamten Masse innerhalb der Kugel auf die Galaxie $$$P$ äquivalent zu, als ob diese Masse an einem einzigen Punkt konzentriert wäre $$$O$ , das ist der Mittelpunkt der Kugel.

Newtonsche Bewegungsgleichungen

Finde den Abstand zwischen Galaxien $$$P$ und $$$O$ . Galaxie $$$P$ hat Koordinaten $$$(x, y, z)$ das heißt, die Entfernung vom Zentrum zur Galaxie $$$P$ gleich

$$

$$D = a (t) \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

Wir können die Notation einführen

$$

$$R = \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

$$$R$ nicht in Metern gemessen, sondern in den gleichen Einheiten wie $$$x$ , $$$y$ und $$$z$ und hängt nicht von der Zeit ab. Dann

$$

$$D = a (t) \, R$$

Wir zeichnen jetzt die Geschwindigkeit und Beschleunigung der Galaxie auf $$$P$

$$

$$\ mathcal {V} = \ dot {a} (t) \, R$$

$$

$$\ mathcal {A} = \ ddot {a} (t) \, R$$

Jetzt müssen wir die Beschleunigung gleichsetzen $$$\ mathcal {A}$ zur Beschleunigung, die mit der gesamten Gravitationsmasse innerhalb einer Kugel mit Radius verbunden ist $$$R$ . Bezeichne die Masse der Galaxie $$$P$ für $$$m$ und die Masse aller Materie innerhalb der Sphäre dahinter $$$M$ . Dann wirkt die Schwerkraft auf die Galaxie $$$P$ ist gleich

$$

$$F = -G \ frac {m \, M} {D ^ 2}$$

wo $$$G = 6.67408 \ times10 ^ {- 11} \ mathrm {N \ cdot m ^ 2 \ cdot kg ^ {- 2}}$ - Gravitationskonstante. Das Minuszeichen in der Formel bedeutet, dass es sich um eine Anziehungskraft handelt.

Jetzt können Sie die Beschleunigung der Galaxie aufzeichnen $$$P$

$$

$$\ mathcal {A} = -G \ frac {M} {D ^ 2}$$

Wir setzen zwei Ausdrücke für gleich $$$\ mathcal {A}$ und bekommen

$$

$$\ ddot {a} (t) \, R = -G \ frac {M} {D ^ 2}$$

Wir berücksichtigen das $$$D = a \, R$ dann

$$

$$\ ddot {a} \, R = - \ frac {M \, G} {a ^ 2 \, R ^ 2}$$

Teilen Sie beide Seiten durch $$$a \, R$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {M \, G} {a ^ 3 \, R ^ 3}$$

Finden Sie das Volumen der Kugel

$$

$$V = \ frac {4} {3} \ pi \, D ^ 3 = \ frac {4} {3} \ pi \, a ^ 3 \, R ^ 3$$

Wir multiplizieren den Zähler und Nenner der rechten Seite mit $$$4 \ pi / 3$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4} {3} \ pi \, G \, \ rho$$

Diese Gleichung ist unabhängig von $$$R$ und es gilt für jede Galaxie im Universum. Diese Gleichung ist die zentrale Grundgleichung der Kosmologie .

Eine der Konsequenzen dieser Gleichung ist, dass das Universum nicht statisch sein kann, wenn es nicht leer ist. Aus dieser Gleichung folgt, dass das Universum nur dann statisch sein kann, wenn es leer ist.

Wir können diese Gleichung angesichts dessen umschreiben $$$\ rho = \ nu / a ^ 3$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4 \ pi} {3} \ frac {G \, \ nu} {a ^ 3}$$

Diese Gleichung wurde zuerst im Kontext der allgemeinen Relativitätstheorie von Alexander Friedman erhalten. Diese Gleichung sagt uns nicht, ob sich das Universum ausdehnt oder zusammenzieht. Es heißt nur, dass die zweite Ableitung des Skalierungsfaktors negativ ist. Das heißt, wenn sich das Universum ausdehnt, verlangsamt es sich, und wenn das Universum schrumpft, beschleunigt es sich.

Tatsächlich dehnt sich das Universum aus und verlangsamt sich nicht. Wir haben einfach getan, was Newton tun konnte und was alle Kosmologen bis etwa 1998 für richtig hielten. Dieses Modell wurde allgemein akzeptiert und als Standardmodell des Universums bezeichnet, bis die beschleunigte Expansion des Universums offen entdeckt wurde. Bisher hat die rechte Seite der Gleichung nur einen Term. Tatsächlich sollte es mehrere Begriffe geben, die sich auf die allgemeine Relativitätstheorie beziehen.

Abfahrtsgeschwindigkeit

Schreiben Sie nun die volle Energie der Galaxie $$$P$ als die Summe der Kinetik und des Potentials

$$

$$E = \ frac {1} {2} m \ mathcal {V} ^ 2 - G \ frac {m \, M} {D}$$

Die Energie kann je nach Verhältnis zwischen diesen beiden Begriffen positiv oder negativ sein. Es ist auch wichtig, sich daran zu erinnern, dass die Gesamtenergie des Partikels $$$P$ gespeichert. Wenn die Gesamtenergie positiv ist, kann das Teilchen nicht zurückkehren. Ein Teilchen kehrt nur zurück, wenn die Gesamtenergie negativ ist. Der Grenzfall ist, dass die Gesamtenergie Null ist. Löse die Gleichung $$$E = 0$ für $$$\ mathcal {V}$ um die Abfahrtsgeschwindigkeit zu finden.

$$

$$\ frac {1} {2} m \ mathcal {V} ^ 2 - G \ frac {m \, M} {D} = 0$$

$$

$$\ mathcal {V} _ {0} = \ frac {2MG} {D}$$

Genau wie eine Galaxie $$$P$ Das gesamte Universum kann eine Geschwindigkeit haben, die höher als die Abfluggeschwindigkeit, niedriger als die Abfluggeschwindigkeit oder gleich der Abfluggeschwindigkeit ist. Wenn die Geschwindigkeit des Universums höher als die Abfluggeschwindigkeit ist, dehnt es sich aus und beginnt nie zu schrumpfen. Wenn das Universum eine Geschwindigkeit hat, die unter der Abfluggeschwindigkeit liegt, beginnt es früher oder später zu schrumpfen.

Schreiben Sie die Gesamtenergiegleichung neu

$$

$$\ frac {1} {2} m \, \ dot {a} ^ 2 R ^ 2 - \ frac {m \, MG} {aR} = E$$

Friedman-Gleichung

Betrachten Sie den Fall, in dem die Geschwindigkeit des Universums mit der Abfluggeschwindigkeit übereinstimmt.

$$

$$\ frac {1} {2} m \, \ dot {a} ^ 2 R ^ 2 - \ frac {m \, MG} {aR} = 0$$

Vereinfachen Sie den Ausdruck: dividieren durch $$$m$ , multipliziere mit 2, dividiere durch $$$a ^ 2 R ^ 2$

$$

$$\ frac {\ dot {a} ^ 2} {a ^ 2} - \ frac {2MG} {a ^ 3R ^ 3} = 0$$

Im zweiten Term multiplizieren wir Zähler und Nenner mit $$$4 \ pi / 3$ . Dann erhalten wir im Nenner das metrische Volumen der Kugel $$$V$ . Angesichts dessen $$$M / V = ​​\ rho$ wir bekommen

$$

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} G \ rho$$

Dies nennt man die Friedman-Gleichung . Es entspricht der oben erhaltenen Newtonschen Gleichung. Da wir angenommen haben, dass die Gesamtenergie Null ist, dehnt sich ein solches Universum aus, verlangsamt sich asymptotisch auf Null, überschreitet jedoch niemals Null und beginnt nicht zu schrumpfen.

Erinnern Sie sich jetzt daran $$$\ rho = \ nu / a ^ 3$ . Schreiben Sie die Friedman-Gleichung neu

$$

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} \ frac {\ nu G} {a ^ 3}$$

Parameter $$$\ nu$ sehr flexibel. . , , $$$\frac{8\pi}{3}\nu G = 1$ .

$$

$$\left(\frac{\dot{a}}{a}\right)^2 = \frac{1}{a^3}$$

Die rechte Seite dieser Gleichung ist immer positiv und daher die Expansionsrate
$$˙ a wird niemals gleich Null. Erinnern Sie sich jetzt daran$\dot{a}$$$˙ a /a=Histder Hubble-Konstantenparameter. Aus der Gleichung folgt auch, dass der Hubble-Parameter niemals das Vorzeichen ändert. Es verlangsamt sich jedoch immer noch. Der Hubble-Parameter wird mit der Zeit immer kleiner. Diese Gleichung ist für die gesamte Kosmologie äußerst wichtig. Eine einfache Möglichkeit, dies zu lösen, besteht darin, nach einer Lösung eines bestimmten Typs zu suchen. Wir werden nämlich nach einer Lösung in der Form suchen$\dot{a}/a = H$

$$

$$a(t) = c\,t^p$$

wo $$$c$ und $$p sind einige Konstanten.$p$

$$

$$\dot{a} = c\,p\,t^{p-1}$$

$$

$$\frac{\dot{a}^2}{a^2} = \frac{p^2}{t^2}$$

$$

$$\frac{p^2}{t^2} = \frac{1}{c^3\,t^{3p}}$$

$$

$$3p = 2\\ p^2 = \frac{1}{c^3}$$

$$

$$p = \frac{2}{3}\\ c = \left(\frac{3}{2}\right)^{\frac{2}{3}}$$

Wir haben eine Lösung für die Friedman-Gleichung erhalten.


Diagramm der Lösung der Friedman-Gleichung

Das reale Universum folgt dieser Entscheidung nur bis zu einem bestimmten Zeitpunkt und beginnt dann zu beschleunigen. Newton könnte das tun. Er kam sehr nahe. Habe die richtigen Fragen gestellt. Der Vortragende ist zuversichtlich, dass Newton dies höchstwahrscheinlich getan und diese Entscheidung erhalten hat. Solche Informationen über das Universum widersprachen jedoch seinen religiösen Ansichten, weshalb er seine Entdeckungen nicht veröffentlichte.