Hallo Geektimes.
Im Prozess des Leerlaufs entstand die Idee, verschiedene Glücksspiele zu studieren und gleichzeitig besser zu verstehen, wie es funktioniert. Die Ergebnisse waren zwar allgemein offensichtlich, aber interessant genug, um sie mit der Öffentlichkeit zu teilen.
Für wen Details interessant sind, frage ich unter Katze.
Würfel: Craps-Spiel
Höchstwahrscheinlich eine intuitiv einfache und verständliche Option - es gibt einen Würfel mit Markierungen von 1 bis 6, und die Wahrscheinlichkeit, dass eine bestimmte Zahl herausfällt, beträgt 1/6. Aber auf diese Weise zu spielen wäre langweilig, daher sind Spiele mit komplexeren Regeln beliebt. Ein beliebtes Glücksspiel ist
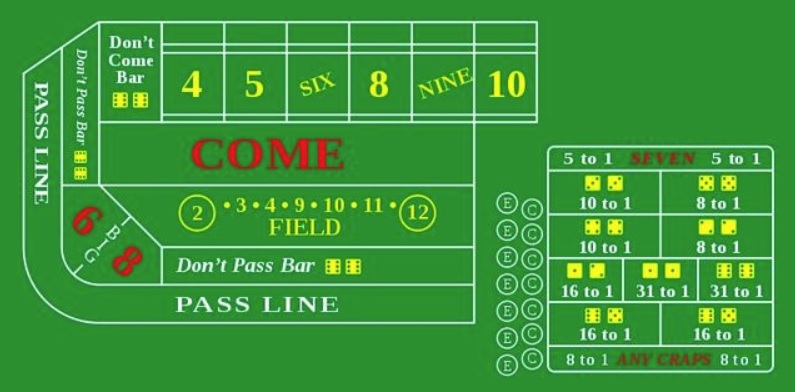
Craps . Das Bild oben zeigt ein Bild des Spieltisches. Wie Sie sehen können, gibt es von allem viel, aber wir werden nicht auf tiefe Feinheiten eingehen.
Jede Spielrunde besteht aus zwei Würfeln, die gesammelten Punkte werden addiert. In dem
Artikel heißt es : „Die Spielregeln sind einfach: Ein Spieler würfelt mit zwei Würfeln, und wenn die Summe der Punkte 7 oder 11 beträgt, gewinnt er, wenn 2, 3 oder 12, verliert er. Wenn ein anderer Betrag auf die Würfel fällt, wirft der Schütze sie zu einer Gewinn- oder Verlustkombination. “
Mal sehen, wie viel Sie auf diese Weise gewinnen können. Es ist nicht notwendig, dafür in ein Casino zu gehen. Wir werden Python verwenden, um das Spiel zu simulieren. Wir schreiben eine Funktion für einen Wurf:
import random def shoot(): return random.randint(1,6) + random.randint(1,6)
Wir werden die Funktion der Simulation eines Zuges gemäß den obigen Regeln schreiben.
def move(): while True: val = shoot() print "Dice roll:", val if val == 7 or val == 11: return True if val == 2 or val == 3 or val == 12: return False
Lassen Sie uns unseren virtuellen Spieler auf einen anfänglichen Betrag von 100 US-Dollar festlegen und den Spielprozess starten. Lassen Sie unseren Spieler 100 Wetten machen, jedes Mal 1u.e.
money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move() if step is True: money_total += bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total
Wir starten die Simulation von 100 Spielen und sind überrascht über das Ergebnis, dass der Spieler
gewonnen hat und mit einer spürbaren Gewinnspanne aus Niederlagen: Gewinn 63, Verlust 37, Geld 126. Wir erhöhen die Anzahl der Spiele auf 1000 und laufen erneut, der Spieler hat erneut gewonnen: Gewinn 680, Verlust 320, Geld 460 .
Es ist klar, dass hier etwas nicht stimmt - ein Spiel, bei dem der Spieler immer schwarze Zahlen schreibt, im Casino kaum beliebt ist, es würde einfach pleite gehen. Versuchen wir es herauszufinden.
Es scheint intuitiv, dass beim Werfen eines Würfels die Wahrscheinlichkeit, dass eine Facette herausfällt, ebenso wahrscheinlich ist. Und das ist wahr, aber im Fall
eines Würfels. Wenn es zwei Würfel gibt, wird alles komplizierter. Zum Beispiel kann die Zahl 7 als 3 + 4, 2 + 5, 1 + 6 herausfallen, aber die Zahl 12 kann nur als eine Kombination von 6 + 6 herausfallen.
Im Jupyter-Notizbuch erstellen wir einen Zeitplan für den Verlust von Beträgen von 1 bis 12 für 100 Würfe:
from matplotlib import pyplot as plt %matplotlib inline y = [ shoot() for v in range(100) ] plt.hist(y)
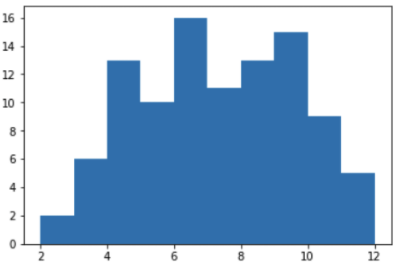
Die Annahme wurde bestätigt, und der Betrag aus dem Zentrum fällt wirklich häufiger aus. Somit fallen die Zahlen 7 und 11 wirklich häufiger aus als 2,3 oder 12. Und die Wahrscheinlichkeit, eine Gewinnkombination „7 oder 11“ zu erhalten, ist wirklich höher.
Wie kann das sein? Leider ist die Antwort einfach - der Autor des oben zitierten Artikels hat die Spielregeln einfach nicht gründlich verstanden. Der Text „Die
Spielregeln sind einfach: Der Spieler würfelt mit zwei Würfeln, und wenn die Summe der Punkte 7 oder 11 beträgt, gewinnt er, wenn 2, 3 oder 12 - er verliert “ ist weit von der Wahrheit entfernt, und die Regeln für Craps sind nicht so einfach, wie sie scheinen .
Die tatsächlichen Regeln für das Wetten auf der Passlinie erwiesen sich als etwas komplizierter (es gibt andere Arten von Wetten, diejenigen, die dies wünschen, können es selbst herausfinden).
Zug 1 : Eine Rolle wird gemacht. Wenn 7 oder 11 fallen, gewinnt der Spieler, wenn 2, 3 oder 12, verliert der Spieler. Wenn eine andere Nummer ausfällt, wird sie unter dem Namenspunkt gespeichert.
Zug 2 : Eine Rolle wird gemacht. Wenn 7 fällt, verliert der Spieler. Wenn der Punkt fällt, hat der Spieler gewonnen. Wenn andere Zahlen fallen, wird der Zug wiederholt (zu diesem Zeitpunkt können die Spieler auch auf andere Zahlen setzen).
In der Tat ist alles etwas komplizierter als in der Originalversion beschrieben. Wir fügen eine Simulationsfunktion hinzu, die genauere Regeln berücksichtigt.
def move(): point = 0 while True: val = shoot() if point == 0:
Das Ergebnis ist jetzt der Wahrheit ähnlicher: Bei 100 Spielen gewann der Spieler 43 Mal, verlor 57 Mal, der Kontostand am Ende des Spiels betrug 86.u. Es ist auch interessant, dass sich die Anzahl der Siege als ziemlich groß herausstellte und nur etwas weniger als 50% beträgt. Dies ist aus Sicht des Casinos eine kompetente Strategie - sie ermöglicht es Ihnen, das Interesse des Spielteilnehmers aufrechtzuerhalten (es wäre uninteressant, ständig zu verlieren), aber gleichzeitig bleibt der Gewinnsaldo des Casinos positiv und der Geldsaldo des Spielers entsprechend negativ.
Lassen Sie uns genauer sehen, was für die Simulation von 100 Spielen erhalten wird.
- Die Gewinnchance im ersten Schritt ging in etwa 20 Fällen zurück.
- Die Chance, beim ersten Schritt sofort zu verlieren, ist in 15 Fällen gesunken.
- In den verbleibenden 65 Fällen geht das Spiel weiter und alles ist schwierig: Die Auswahl erfolgt aus zwei Zahlen, 7 und Punkt. Wie Sie der obigen Grafik entnehmen können, ist die Wahrscheinlichkeit, dass eine „verlorene“ Zahl 7 ausfällt, maximal, was im Allgemeinen bewiesen werden sollte.
Es ist interessant festzustellen, dass die Gewinnchance bei 45% ziemlich hoch ist. Ist es also möglich zu gewinnen? Kurzfristig, zum Beispiel in einer anderen Simulation, hatte der Spieler „Glück“ und in 100 Spielen erhöhte er sein virtuelles Kapital von 100 auf 112ye.
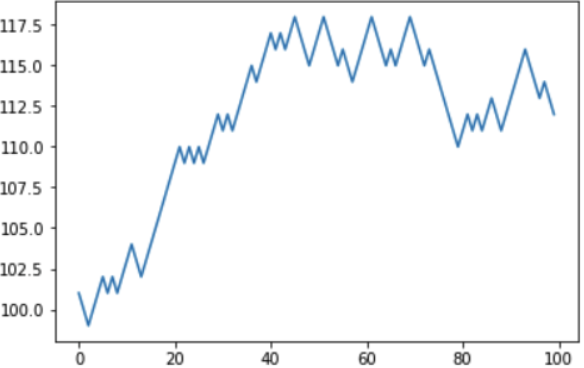
Aber schon die nächste Simulation zeigte ein negatives Gleichgewicht: Der Spieler reduzierte seinen Zustand von 100 auf 88ye, nachdem er übrigens die gleichen 12ye verloren hatte, die er zuvor „gewonnen“ hatte.
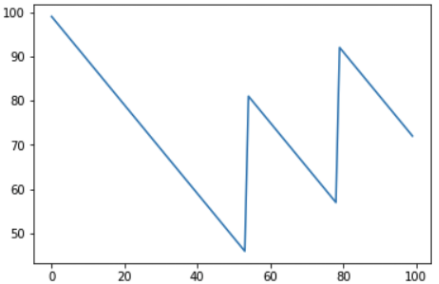
Wenn Sie die Anzahl der Iterationen auf 1000 erhöhen, können Sie sehen, wie das Geldguthaben des Spielers auf lange Sicht aussehen könnte:
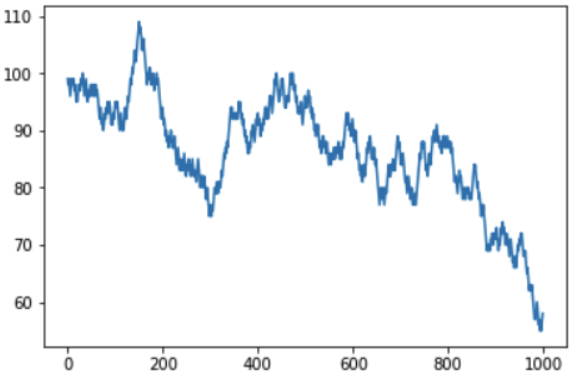
Es ist klar, dass mit einer Gewinnchance von weniger als 50% für jedes Spiel der resultierende Geldbetrag auf dem Konto des Spielers allmählich abnimmt und der Betrag des Casino-Gewinns allmählich zunimmt. Auf der Karte sind übrigens Ausbrüche und Stürze sichtbar, und es kann sich eine vernünftige Frage stellen - können sie vorhergesagt werden? Ach nein, weil Würfelwürfe sind Ereignisse, die unabhängig voneinander sind, und frühere Ergebnisse haben keinerlei Einfluss auf Folgendes. Sie können die Hauptidee noch einmal wiederholen - Sie können ein oder sogar mehrere Male gewinnen, aber auf lange Sicht ist es unmöglich, im Casino im Plus zu bleiben. Die Spielregeln werden so aufgestellt, dass das Gleichgewicht nicht zugunsten des Spielers ist.
Es gibt andere Arten von Wetten im Craps-Spiel, und diejenigen, die dies wünschen, können sie selbst analysieren.
Amerikanisches Roulette
Die nächste beliebte Art des Glücksspiels ist Roulette, wenn man die amerikanische Version betrachtet.
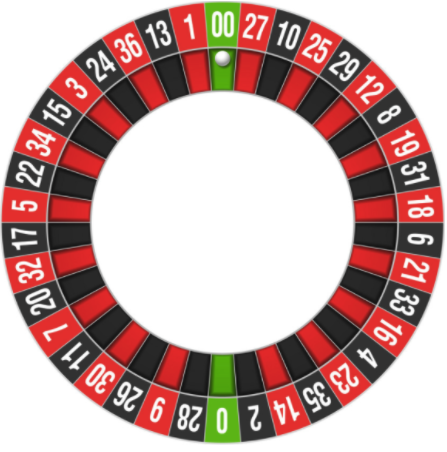
Das Roulette-Spielfeld ist in 38 Zellen unterteilt: 36 Zonen mit Zahlen + 2 Zonen „Null“ und „Doppelte Null“. Ein Ball, der auf ein Roulette-Rad geworfen wird, stoppt offensichtlich in einer der Zonen. Der Spieler kann eine Vielzahl von Wetten abschließen, von denen es mehr als 10 Arten gibt. Betrachten Sie einige davon.
Schwarz-Rot (oder gerade-ungerade)Ein Spieler gewinnt, wenn die Wette, die er nennt, übereinstimmt. Offensichtlich wäre die Wahrscheinlichkeit von Schwarz oder Rot 50/50, wenn es nicht zwei Felder mit Null gäbe - wenn sie sie treffen, verliert die Wette. Wie bei Craps beträgt die Gewinnwahrscheinlichkeit nur etwas weniger als 50% - aber dieses „leichte“ reicht aus, um rote Zahlen zu schreiben.
Wir werden die Funktion der Simulation der Bewegung mit Zufallszahlen von 1 bis 38 schreiben, die letzten 2 Ziffern werden als "Null" betrachtet.
def move_roulette1(): val = random.randint(1,38) if val == 37 or val == 38: return False return val % 2 != 0
Führen Sie die Simulation für 100 Spiele aus. Der Code ist der gleiche wie in der Craps-Simulation. Wir ändern nur den Funktionsaufruf.
money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move_roulette1() if step is True: money_total += bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total
Ergebnis: In 100 Versuchen gewann der Spieler 46 Mal und verlor 54 Mal. Die Grafik zeigt, dass der Spieler sowohl "Höhen" als auch "Stürze" hatte, aber das endgültige Gleichgewicht ist immer noch negativ.
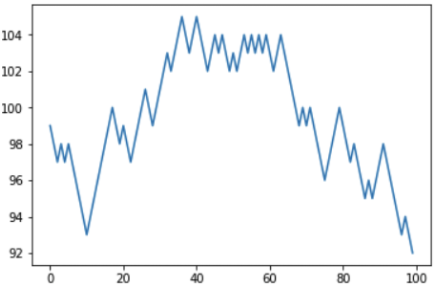
Je mehr wir spielen, desto tiefer gehen wir in das Minus und das Casino in das Plus:
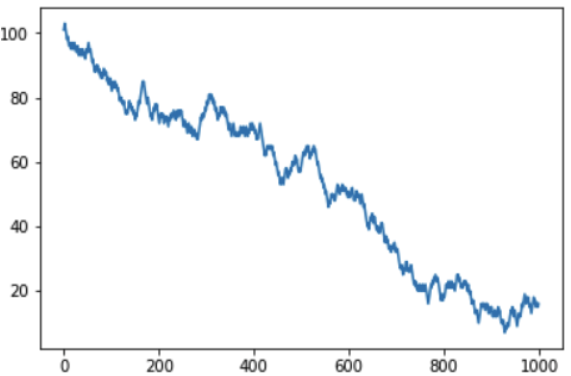
Es gab eine Frage des Lesers, warum ich europäisches Roulette mit einem „Null“ -Feld nicht in Betracht gezogen habe - wie Sie sich vorstellen können, ist die Gewinnchance dort wirklich höher, aber das allgemeine Prinzip ändert sich nicht. Tatsächlich liegt der Unterschied nur in der "Geschwindigkeitsabnahme". Hier ist der gemeinsame Zeitplan für die amerikanische und europäische Version des Spiels:
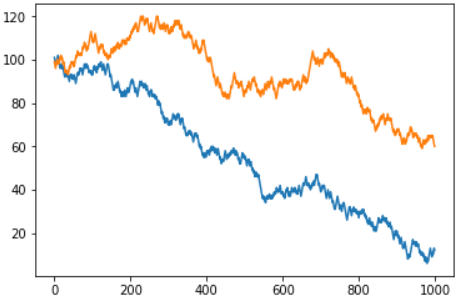
Wer die europäische Roulette-Version mit 37 Slots testen möchte, kann die zweite Option der Funktion nutzen:
def move_roulette1(): val = random.randint(1,37) if val == 37: return False return val % 2 != 0
Wetten Sie auf eine bestimmte ZahlDer Spieler kann auch auf eine bestimmte Zahl setzen, die Wette auf den Gewinn beträgt 35: 1. Es scheint großartig, aber es ist leicht zu erraten, dass die Wahrscheinlichkeit, dass eine bestimmte Roulette-Zahl herausfällt, 1:38 beträgt, d. H. wieder etwas weniger.
Fügen wir die Wettfunktion einer bestimmten Zahl hinzu:
def move_roulette2(num): val = random.randint(1,38) return val == num
Simulation nehmen wir an, dass der Spieler die Nummer 10 setzt:
money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move_roulette2(10) if step is True: money_total += 35*bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total
Infolgedessen hat der Spieler 2 Mal gewonnen und 98 Mal verloren, der endgültige Kontostand beträgt -28.u.
 Wetten Sie auf zwei Zahlen
Wetten Sie auf zwei ZahlenSie können auf zwei Zahlen setzen - die Gewinnchance ist höher, aber die Wette ist geringer und beträgt 17: 1.
Schreiben wir eine Funktion:
def move_roulette3(num1, num2): val = random.randint(1,38) return val == num1 or val == num2
Für 100 Versuche unserer Simulation gewann der Spieler 3 Mal und verlor 97 Mal, der Kontostand betrug -46u.e.
Es gibt andere Arten von Wetten, zum Beispiel für 4 Zahlen mit einem Koeffizienten von 1: 8, diejenigen, die es wünschen, können selbst experimentieren. Wie Sie sich vorstellen können, sind alle Gewinnchancen so ausgelegt, dass der Spieler rote Zahlen schreibt. Es scheint verlockend, 1ye auf die Zahl zu setzen, um bis zu 35ue zu gewinnen. Aber der Gewinnbetrag erhöht sich um das 35-fache und die Gewinnchance verringert sich um das 38-fache - der endgültige Saldo wird weiterhin zugunsten des Casinos sein.
Lotto 6 von 45
Das nächste, was interessant zu überprüfen ist, ist Lotto. Das Prinzip des Spiels ist recht einfach: Es gibt 45 Bälle in der Trommel, von denen 6 zufällig fallen. Der Ticketpreis laut Gosloto-Website beträgt 100 Rubel und der Preis hängt von der Anzahl der erratenen Bälle ab. Die ungefähre Reihenfolge der Gewinne lautet wie folgt: 2 erratene Bälle ergeben einen Gewinn von 100r, 3 erratene Bälle ergeben 300r, 4 Bälle - 3000r, 5 Bälle - 300.000r und 6 Bälle - ein Superpreis von etwa 10.000.000r.
Schreiben Sie zunächst ein Programm zum Werfen von Bällen und zum Vergleichen des Ergebnisses:
def lottery(values): balls = range(1, 45+1) b1 = balls.pop(random.randint(0, len(balls)-1)) b2 = balls.pop(random.randint(0, len(balls)-1)) b3 = balls.pop(random.randint(0, len(balls)-1)) b4 = balls.pop(random.randint(0, len(balls)-1)) b5 = balls.pop(random.randint(0, len(balls)-1)) b6 = balls.pop(random.randint(0, len(balls)-1)) s = [b1,b2,b3,b4,b5,b6] res = list(set(s) & set(values)) return len(res)
Ein zufälliger Ball "bekommt" 6 Mal aus dem Ballarray, dann wird die Anzahl der Schnittelemente zweier Sätze bestimmt. Jetzt erstellen wir ein Diagramm des Gesamtgewinns aus der Anzahl der gekauften Tickets. Der Einfachheit halber nehmen wir an, dass der Spieler auf die gleichen Zahlen setzt.
money = [] money_total = 0 ticket_price = 100 for p in xrange(N): val = lottery([3,7,12,18,33,28]) if val == 2: money_total += 100 if val == 3: money_total += 300 if val == 4: money_total += 3000 if val == 5: money_total += 300000 if val == 6: money_total += 10000000 money.append(money_total) x = range(0, N) price = map(lambda x: ticket_price*x, x) from matplotlib import pyplot as plt %matplotlib inline plt.plot(price, money)
Um die Größenordnung zu verstehen: Wenn Sie 100 Tickets kaufen (der Gesamtbetrag beträgt 10.000 R), ergibt dies 14 erratene „doppelte“ Bälle und einen erratenen „dreifachen“. Der Gesamtgewinn beträgt ungefähr 2000r bei 10.000r ausgegeben.
Der Auszahlungsplan für den ausgegebenen Betrag ist nahezu linear:

Es stellt sich heraus, dass der Gewinn 250.000 beträgt, wenn Sie Tickets in einer Million kaufen. Der „Superpreis“ in der Simulation ist nie herausgefallen, obwohl dies theoretisch durchaus möglich ist. Übrigens, wie in den Regeln geschrieben, beträgt der Preispool 50% der verkauften Tickets, aber der „Superpreis“ fällt nicht immer aus, so wie beim Casino gewinnen die Organisatoren natürlich immer.
Spielautomaten
Sie arbeiten auch nach einem (Pseudo-) Zufallsprinzip, "Pseudo", weil Der Code in ihnen ist seit langem programmatisch und hat keine saubere Mechanik. Die oben für Spielautomaten beschriebenen allgemeinen Prinzipien funktionieren ebenfalls, und die Grafiken werden höchstwahrscheinlich nicht anders sein. Wer möchte, kann die Simulationsfunktion selbst hinzufügen.
Ein guter Artikel über das Design von Spielautomaten wurde bereits über Geektimes veröffentlicht.
Fazit
Vielleicht hat dieser Artikel Amerika nicht für viele geöffnet, aber in den Grafiken ist er im Prinzip visueller. Es stellte sich als interessanter heraus, einen grundlegend anderen psychologischen Ansatz mit dem Spiel zu vergleichen. Gewinne in der Lotterie sind möglicherweise groß, aber sehr selten. In Casinos ist der Ansatz umgekehrt - die Wetten sind so eingerichtet, dass eine Person so oft wie möglich gewinnt. Nach 10 Spielen in einem Casino gewinnt eine Person 4 Mal und verliert 6 Mal. Dies ermöglicht es dem Spieler, das Interesse an dem Spiel nicht zu verlieren, aber in jedem Fall bleibt das Gesamtgleichgewicht negativ - eine Person wird viele Male gewinnen, aber auch
etwas mehr verlieren.
Vielleicht ist das schon so offensichtlich, aber der Artikel handelt nur von Spielen, die auf Zufälligkeit basieren, nicht von Poker, Karten, Schach usw. Kann es in solchen zufälligen Spielen eine „Gewinnstrategie“ geben? Offensichtlich nicht, weil Weder Knochen noch Ball noch Lottoscheine haben ein Gedächtnis, und ihr Verhalten hängt nicht von früheren Iterationen ab. Übrigens ist es wichtig, sich an diesen Moment zu erinnern - intuitiv kann eine Person nach mehrmaliger Niederlage entscheiden, dass sie jetzt „definitiv“ gewinnt. Leider gibt es kein Roulette oder Würfel und sie wissen nichts über die Anzahl der vorherigen Versuche. Jedes Spiel beginnt im Wesentlichen mit einer sauberen Tafel.
Beantwortung der Frage im Titel des Artikels - ist es möglich, Glücksspiel zu gewinnen? Wie die Simulation zeigt, ist es im Prinzip möglich, dass die Wahrscheinlichkeitstheorie dies zulässt. Aber nicht lange - es lohnt sich, das 2., 3., ... N-te Mal zu spielen, wenn das Gleichgewicht sinkt. Auf lange Sicht ist es unmöglich, im Casino zu gewinnen.
PS: Für diejenigen, die experimentieren möchten, ist der Quellcode in einer Datei unter dem Spoiler angeordnet. Es kann beispielsweise
hier in der Online-Python-IDE ausgeführt
werden . Um die europäische Version des Roulettes anstelle der amerikanischen zu testen, reicht es aus, 38 bis 37 im Code zu ändern. Diese Simulation ist recht einfach und berücksichtigt nicht verschiedene zusätzliche Faktoren, wie den Geldbetrag eines Spielers oder das Limit für Wetten in einem Casino. Wer dies wünscht, kann dies alles unabhängig hinzufügen. Unter dem Spoiler können Sie auch eine Videoversion dieses Artikels ansehen.
Quellcode import random def craps(): point = 0 while True: val = shoot()