Spaß beiseite, das Thema ist ernst, Brandgefahr. Lass uns gehen. Dies ist der dritte Artikel in der Reihe, in dem Modelle zur Schätzung des maximalen Stroms der gedruckten Spur erörtert werden. Dies ist in einigen Situationen ein entscheidender Parameter bei der Auswahl der Dicke der leitenden Schichten der Leiterplatte.
In einem
früheren Artikel wurde gesagt, dass die Wahl der Dicke der Kupferschichten einer Leiterplatte zunächst durch das erforderliche Mindestspiel und die Mindestbreite des Leiters sowie den maximalen Strom, der durch den Leiter fließt, bestimmt wird. Diese Parameter können sich widersprechen: Je dünner die leitende Schicht ist, desto kleiner kann das topologische Muster erhalten werden, aber desto kleiner ist der maximale Strom, dem der Druckpfad standhalten kann (ceteris paribus, Breite des Leiters, Stromfrequenz, Kühlkörper usw.). Die Wärmeenergie Q, die am ohmschen Widerstand R der gedruckten Spur freigesetzt wird (Joule-Wärme Q = I
2 Rt, wobei I die Stromstärke, t die Zeit ist), bewirkt, dass ihre Temperatur relativ zur Umgebung ansteigt, was zu einer Überhitzung des Leiters selbst und verwandter Komponenten führt, oder als letztes Mittel zum Ausbrennen bei einem Grenzstrom (englischer Schmelzstrom). Die Korrelation zwischen dem Strom durch die Druckspur und dem Temperaturanstieg hängt von vielen Parametern ab und ist im Allgemeinen schwer vorstellbar. Es gibt jedoch Formeln, mit denen wir vorläufige Schätzungen vornehmen können.
Price, Onderdonk und Brooks
Einer der ersten Versuche wurde von W. H. Pris (WHPreece) unternommen. Seine empirische Abhängigkeit erhielt er in einem Laborexperiment, in dem er den Strom durch den Leiter allmählich erhöhte, bis er rot leuchtet. Die Pris-Formel bezieht den Glühstrom auf den Durchmesser des Leiters d für verschiedene Materialien:
wobei K eine Tabellenkonstante ist, die für Kupfer ungefähr gleich 80 ist. Unter Verwendung des Verhältnisses der Kreisfläche können wir diese Formel für den Fall eines Kupferleiters mit einer Querschnittsfläche S umschreiben:
Im Pris-Experiment wurde der Leiter im Gegensatz zu einem Leiter auf einer Leiterplatte, für die die Kühlkörperbedingungen völlig unterschiedlich sind, in der Luft aufgehängt. Näher sind die Kühlkörperbedingungen für Fälle eines einzelnen Verbindungsleiters sowie für einige Fälle des Mikrodrahtschweißens (wenn das Compoundieren nicht zum Schutz verwendet wird), bei denen diese Formel eine gute Schätzung für den Grenzstrom liefern kann.
Der akzeptable Temperaturanstieg der Druckspur wird üblicherweise als 10-30 ° C angesehen. Dieser Wert kann abhängig von den Projektparametern größer sein. Über den gesamten Bereich der Produktbetriebstemperaturen sollte die Spurtemperatur jedoch niedriger sein als die Glasübergangstemperatur des Leiterplattenmaterials (englische Glasübergangstemperatur, T
g ) und umso mehr die Temperatur des Kupfers Daher ist die von Brooks in [1] nützliche Abhängigkeit des Temperaturanstiegs ∆T vom Strom I der gedruckten Spur mit der Breite w und der Foliendicke h nützlich:
wobei C, α, β, γ Konstanten sind, deren Werte für die äußere und innere Schicht in Tabelle 1 angegeben sind. Es ist zu beachten, dass auf den äußeren Schichten die Foliendicke aufgrund des zusätzlichen Sprühens beim Erzeugen eines Übergangs gewöhnlich 20 bis 40 Mikrometer größer als der Basiswert ist Löcher. Auch der Effekt des Finishs auf Brettern ohne Maske kann erheblich sein. Dies wird in Leistungsgeräten verwendet, wenn ein zusätzliches Lot auf die gedruckte Spur gelötet wird, die von der Maske geöffnet wird.
Eine andere bekannte Formel zur Berechnung der endgültigen Stromtragfähigkeit eines Leiters ist die Onderdonk-Formel (englisch IMOnderdonk), die einen so wichtigen Parameter wie die Zeit enthält. Sie bezieht sich auf die Zeit t des Durchgangs des Stroms I durch einen Kupferleiter mit einem Querschnitt S und den Temperaturanstieg ∆T relativ zur Anfangstemperatur T
0 :
Da bei der Ableitung der Formel [2] eine Wärmeabfuhr ausgeschlossen ist, gilt diese Formel für den Fall einer Druckspur für einen kurzen Stromimpuls von bis zu 1-2 Sekunden. Mit zunehmender Zeit und dem Einfluss der Wärmeabfuhr nimmt die Genauigkeit der Schätzung ab, wodurch der Grenzstrom erheblich verringert wird. Die Abhängigkeitsgraphen für alle drei der obigen Formeln für verschiedene Parameter der Druckspur sind in den 1 und 2 gezeigt.
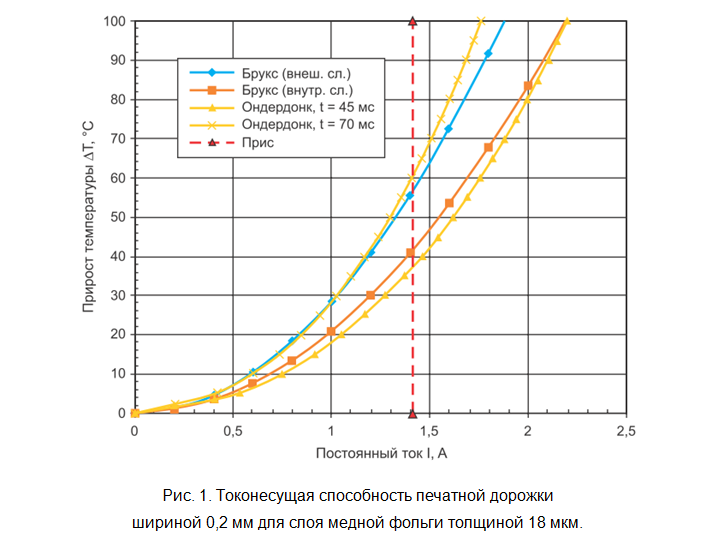

Es ist immer wichtig, die experimentellen Bedingungen oder analytischen Annahmen bei der Ableitung zu berücksichtigen, um die Grenzen der Anwendbarkeit einer bestimmten Formel zu verstehen. Keine der obigen Formeln ergibt eine genaue und optimale Beziehung zwischen dem Grenzstrom und dem erforderlichen Querschnitt des Leiters für reale Anwendungen. Gleiches gilt für einfache Taschenrechner, die beispielsweise im Internet zu finden sind, da sie auf diesen oder ähnlichen Formeln basieren. Der Einfluss benachbarter Leiter und Komponenten als Quellen und Empfänger von Wärme, Strahlung, aktiver oder passiver Kühlung kann nur bei der thermoelektrischen Modellierung in speziellen CAD-Systemen (wie Cadence, ANSYS und anderen) berücksichtigt werden. Selbst in diesem Fall können die Ergebnisse der Modellierung und des Experiments erheblich variieren. Tatsache ist, dass die Druckspur keinen rechteckigen Querschnitt hat, sondern nahezu trapezförmig ist (Abb. 3), und dass ihre Breite und Leitfähigkeit der Kupferfolie nicht nur von den vom Modell berechneten abweichen können, sondern auch eine gewisse Streuung von Probe zu Probe, Charge aufweisen zu chargen, hersteller zu hersteller usw. Der Einfluss von Abweichungen der Breite nimmt mit abnehmender Wirkung zu. Trotzdem stellen die berechneten Ergebnisse anhand von Formeln und Empfehlungen der Standards meistens den schlimmsten Fall dar und bieten somit einen Sicherheitsspielraum für das System. Wenn der Entwickler das Verhältnis zwischen dem Grenzstrom und dem erforderlichen Querschnitt der gedruckten Spur optimieren muss, muss dieses Ziel durch iterative Modellierung und Experiment erreicht werden.

Hauteffekt
Eine Vergrößerung des Querschnitts der gedruckten Spur verringert proportional ihren ohmschen Widerstand pro Längeneinheit, wodurch der Wärmeverlust während des Gleichstromflusses verringert wird. Die Situation mit Wechselstrom ist aufgrund des Vorhandenseins eines Hauteffekts (englischer Hauteffekt) nicht so einfach, was dazu führt, dass die Dichte des Wechselstroms ungleichmäßig über den Querschnitt des Leiters verteilt ist und von der Oberfläche des Leiters zum Zentrum exponentiell auf Null abnimmt. Zur Vereinfachung der Berechnungen wird das Konzept des effektiven Abschnitts des Leiters mit einer durch das Verhältnis bestimmten Tiefe verwendet:
wobei f die Stromfrequenz ist, σ die Metallleitfähigkeit ist, μ die magnetische Permeabilität ist. Bei einer Tiefe gleich δ wird die Stromdichte e-mal kleiner als die Stromdichte auf der Oberfläche J
S. Mathematisch kann die folgende ungefähre Gleichheit für die Stromdichte J (x, y) im Leiter gezeigt werden:
Das heißt, für ungefähre Berechnungen können wir annehmen, dass der Strom nur in der Grenzschicht des Umfangsleiters l der Tiefe δ und mit einer gleichmäßigen Verteilung fließt (Abb. 4).

Wenn im Rahmen dieses vereinfachten Modells die Tiefe der Oberflächenschicht weniger als die Hälfte der Dicke der Druckspur beträgt, wird die Impedanz der Druckspur bei einer bestimmten Frequenz durch diesen effektiven Abschnitt bestimmt, was zu einer Zunahme des ohmschen Widerstands und einer leichten Abnahme der Induktivität führt. In Abb. Fig. 5 zeigt die Abhängigkeit der Tiefe der Oberflächenschicht von der Frequenz des Stroms unter Berücksichtigung der Streuung der Leitfähigkeit des abgeschiedenen Kupfers. Daraus ist ersichtlich, dass für Kupferschichten mit einer Dicke von 18 & mgr; m die Grenzfrequenz (oberhalb derer der Hauteffekt eine Rolle spielt) im Bereich von 50 bis 70 MHz liegt und für Schichten mit einer Dicke von 35 & mgr; m im Bereich von 15 bis 20 MHz. Beachten Sie, dass bei Frequenzen über 100 MHz die Tiefe des Hauteffekts geringfügig variiert. Dies ermöglicht es uns, seine Abhängigkeit von der Frequenz bei den Berechnungen für Hochfrequenzsignale zu vernachlässigen.
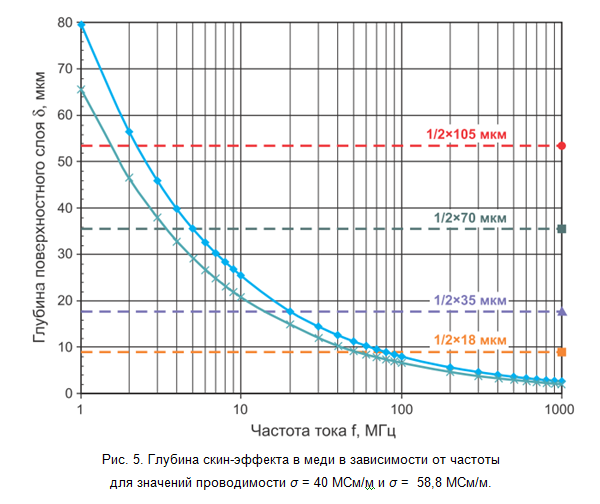
Bei der Konstruktion von Leiterplatten mit konstanten Strömen von mehreren Ampere müssen thermische Berechnungen sowohl für elektrische Komponenten als auch für Leiter durchgeführt werden. Die vorgestellten Modelle und analytischen Beziehungen ermöglichen es uns, den maximalen Strom gedruckter Spuren abzuschätzen und auf dieser Grundlage die erforderliche Dicke der Kupferschichten und die Topologie der Leiter auszuwählen. Um die genaue Lösung zu erhalten, müssen spezielle CAD-Systeme verwendet werden, und es ist wünschenswert, die Geometrie unter Berücksichtigung von Herstellungsfehlern und Kupferleitfähigkeitsdaten zu spezifizieren, die vom Hersteller von Leiterplatten erhalten wurden. Ich empfehle dringend,
Artikel von D. Brooks zu lesen, die sich mit einer detaillierten Analyse von Methoden zur Schätzung der Temperatur gedruckter Leiter befassen und visuelle Ergebnisse der Modellierung von Temperaturfeldern liefern.
Literatur
[1] Brooks DG, Adam J. "Spurenströme und Temperaturen überarbeitet", UltraCAD, 2015.
[2] Adam J., GD Brooks, „Auf der Suche nach Preece und Onderdonk“, UltraCAD, 2015.
Der Artikel wurde erstmals in der Zeitschrift Components and Technologies 2018, Nr. 1 veröffentlicht. Die Veröffentlichung auf Geektimes wurde mit den Herausgebern des Magazins vereinbart.