In unserem Blog über Habré haben wir angepasste Übersetzungen von Materialien aus dem Blog The Financial Hacker veröffentlicht, die sich mit Fragen der Entwicklung von Strategien für den Handel an der Börse befassen. Zuvor haben wir die
Suche nach Marktineffizienzen , die Erstellung von
Modellen für Handelsstrategien und die
Prinzipien ihrer Programmierung erörtert. Heute konzentrieren wir
uns auf die Verwendung von Ansätzen des maschinellen Lernens, um die Effizienz von Handelssystemen zu verbessern.
Der erste Computer, der die Schachweltmeisterschaft gewann, war Deep Blue. Das war 1996 und weitere zwanzig Jahre vergingen, bis es einem anderen Programm, Alpha Go, gelang, den besten Spieler in Go zu besiegen. Deep Blue war ein modellorientiertes System mit eingebetteten Schachregeln. AplhaGo ist ein Data Mining-System, ein tiefes neuronales Netzwerk, das mit Tausenden von Spielen in Go trainiert wurde. Das heißt, um einen Schritt von Siegen über Schachmeister zu machen und die Top-Spieler in Go zu dominieren, war kein verbessertes Stück Eisen notwendig, sondern ein Durchbruch im Bereich Software.
Im aktuellen Artikel werden wir die Anwendung des Data Mining-Ansatzes zur Erstellung von Handelsstrategien in Betracht ziehen. Diese Methode berücksichtigt keine Marktmechanismen, sondern scannt einfach Preiskurven und andere Datenquellen, um nach Vorhersagemustern zu suchen. Maschinelles Lernen oder „künstliche Intelligenz“ sind hierfür nicht immer erforderlich. Im Gegenteil, sehr oft funktionieren die beliebtesten und rentabelsten Methoden des Data Mining ohne Schnickschnack in Form von neuronalen Netzen oder Unterstützung für Vektormethoden.
Prinzipien des maschinellen Lernens
Der trainierte Algorithmus wird mit Datenproben gespeist, die normalerweise irgendwie aus historischen Wechselkursen extrahiert werden. Jede Stichprobe besteht aus n Variablen x1 ... xn, die üblicherweise als Prädiktoren, Funktionen, Signale oder einfacher als Eingabedaten bezeichnet werden. Diese Prädiktoren können die Preise der letzten n Balken im Preisdiagramm oder eine Reihe von Werten klassischer Indikatoren oder andere Funktionen der Preiskurve sein (es gibt sogar Fälle, in denen einzelne Pixel des Preisdiagramms als Prädiktoren für ein neuronales Netzwerk verwendet werden!). Jede Stichprobe enthält normalerweise auch eine bestimmte Zielvariable y, beispielsweise das Ergebnis der nächsten Transaktion nach Analyse der Stichprobe oder der nächsten Preisbewegung.
In der Literatur wird y oft als Bezeichnung oder Ziel bezeichnet. Während des Lernprozesses lernt der Algorithmus, das Ziel y basierend auf den Prädiktoren x1 ... xn vorherzusagen. Was sich das System im Prozess „merkt“, wird in einer Datenstruktur gespeichert, die als Modell bezeichnet wird, das für einen bestimmten Algorithmus spezifisch ist (es ist wichtig, dieses Konzept nicht mit einem Finanzmodell oder einer modellorientierten Strategie zu verwechseln). Ein maschinelles Lernmodell kann Funktionen mit Vorhersageregeln sein, die unter Verwendung von C-Code geschrieben wurden, der durch den Lernprozess erzeugt wird. Oder es könnte sich um eine Reihe von Gewichten handeln, die mit dem neuronalen Netzwerk zusammenhängen:
Training: x1 ... xn, y => Modell
Vorhersage: x1 ... xn, Modell => y
Prädiktoren, Funktionen oder wie auch immer Sie sie aufrufen möchten, sollten Informationen enthalten, die ausreichen, um Vorhersagen über den Wert des Ziels y mit einer bestimmten Genauigkeit zu generieren. Sie müssen außerdem zwei formale Kriterien erfüllen. Erstens müssen alle Prädiktorwerte im gleichen Bereich liegen, z. B. -1 ... +1 (für die meisten Algorithmen auf R) oder -100 ... +100 (für Algorithmen in den Skriptsprachen Zorro oder TSSB). Bevor Sie Daten an das System senden, müssen Sie sie normalisieren. Zweitens müssen die Abtastwerte ausgeglichen sein, dh gleichmäßig über die Werte der Zielvariablen verteilt sein. Das heißt, Sie sollten die gleiche Anzahl von Stichproben haben, die zu einem positiven Ergebnis führen und Sätze verlieren. Wenn diese beiden Anforderungen nicht erfüllt werden, sind gute Ergebnisse nicht erfolgreich.
Regressionsalgorithmen generieren Vorhersagen über numerische Werte wie die Größe oder das Vorzeichen der nächsten Preisbewegung. Klassifizierungsalgorithmen sagen quantitative Klassen von Stichproben voraus, beispielsweise, ob sie dem Gewinn oder Verlust von Geldern vorausgehen. Einige Algorithmen wie neuronale Netze, Entscheidungsbäume oder Unterstützungsvektormethoden können in beiden Modi ausgeführt werden.
Es gibt auch Algorithmen, die lernen können, aus Klassenproben zu extrahieren, ohne dass ein Ziel y erforderlich ist. Dies wird als unbeaufsichtigtes Lernen bezeichnet, im Gegensatz zu überwachtem Lernen. Irgendwo zwischen diesen beiden Methoden befindet sich das „Verstärkungslernen“, bei dem das System durch Ausführen von Simulationen mit bestimmten Funktionen trainiert und das Ergebnis als Ziel verwendet. Ein Anhänger von AlphaGo, einem System namens AlphaZero, nutzte verstärktes Lernen und spielte eine Million Go-Spiele mit sich selbst. Im Finanzbereich sind solche Systeme oder Produkte, die unbeaufsichtigtes Lernen verwenden, äußerst selten. 99% der Systeme verwenden überwachtes Lernen.
Unabhängig davon, welche Signale wir für Prädiktoren im Finanzbereich verwenden, enthalten sie in den meisten Fällen viel Rauschen und wenig Informationen und sind darüber hinaus instabil. Finanzielle Prognosen sind daher eine der schwierigsten Aufgaben des maschinellen Lernens. Komplexere Algorithmen erzielen hier bessere Ergebnisse. Die Auswahl der Prädiktoren ist entscheidend für den Erfolg. Es müssen nicht unbedingt viele vorhanden sein, da dies zu Umschulungen und Fehlfunktionen führt. Daher verwenden Data Mining-Strategien häufig einen vorgewählten Algorithmus, der eine kleine Anzahl von Prädiktoren aus einem größeren Pool extrahiert. Eine solche vorläufige Auswahl kann auf der Korrelation zwischen Prädiktoren, ihrer Bedeutung, ihrem Informationsreichtum oder einfach auf dem Erfolg / Misserfolg der Verwendung der Testsuite beruhen. Praktische Experimente zur Zielauswahl finden Sie beispielsweise im
Robot Wealth- Blog.
Nachfolgend finden Sie eine Liste der beliebtesten Methoden des Data Mining im Finanzbereich.
1. Suppe von Indikatoren
Die meisten Handelssysteme basieren nicht auf Finanzmodellen. Oft benötigen Händler nur Handelssignale, die von bestimmten technischen Indikatoren generiert werden und die von anderen Indikatoren in Kombination mit zusätzlichen technischen Indikatoren gefiltert werden. Wenn er einen Händler fragt, wie eine solche Mischung von Indikatoren zu einer Art Gewinn führen kann, antwortet er normalerweise wie folgt: „Glaub mir, ich tausche meine Hände und alles funktioniert.“
Und das ist die Wahrheit. Zumindest manchmal. Obwohl die meisten dieser Systeme den
WFA-Test nicht bestehen (und einige lediglich historische Daten testen), funktioniert eine überraschend große Anzahl solcher Systeme letztendlich und erzielt einen Gewinn. Der Autor des Blogs Financial Hacker beschäftigt sich mit der Entwicklung kundenspezifischer Handelssysteme und erzählt die Geschichte eines Kunden, der systematisch mit technischen Indikatoren experimentierte, bis er eine Kombination fand, die für bestimmte Arten von Vermögenswerten funktioniert. Diese Trial-and-Error-Methode ist ein klassischer Ansatz für das Data Mining. Für den Erfolg benötigen Sie sie nur, viel Glück und viel Geld für Tests. Daher können Sie manchmal mit einem profitablen System rechnen.
2. Kerzenmuster
Nicht zu verwechseln mit Kerzenmustern, die es seit Hunderten von Jahren gibt. Das moderne Äquivalent dieses Ansatzes ist der Handel auf der Grundlage von Preisbewegungen. Sie analysieren auch die offenen, hohen, niedrigen und geschlossenen Indikatoren für jede Kerze im Diagramm. Jetzt verwenden Sie Data Mining, um die Kerzen der Preiskurve zu analysieren und Muster hervorzuheben, mit denen Vorhersagen über die Richtung der Preisbewegung in der Zukunft erstellt werden können.
Zu diesem Zweck gibt es ganze Softwarepakete. Sie suchen nach Mustern, die in Bezug auf benutzerdefinierte Kriterien rentabel sind, und verwenden sie, um eine Mustererkennungsfunktion aufzubauen. All dies könnte ungefähr so aussehen:
int detect(double* sig) { if(sig[1]<sig[2] && sig[4]<sig[0] && sig[0]<sig[5] && sig[5]<sig[3] && sig[10]<sig[11] && sig[11]<sig[7] && sig[7]<sig[8] && sig[8]<sig[9] && sig[9]<sig[6]) return 1; if(sig[4]<sig[1] && sig[1]<sig[2] && sig[2]<sig[5] && sig[5]<sig[3] && sig[3]<sig[0] && sig[7]<sig[8] && sig[10]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; if(sig[1]<sig[4] && eqF(sig[4]-sig[5]) && sig[5]<sig[2] && sig[2]<sig[3] && sig[3]<sig[0] && sig[10]<sig[7] && sig[8]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; if(sig[1]<sig[4] && sig[4]<sig[5] && sig[5]<sig[2] && sig[2]<sig[0] && sig[0]<sig[3] && sig[7]<sig[8] && sig[10]<sig[11] && sig[11]<sig[9] && sig[9]<sig[6]) return 1; if(sig[1]<sig[2] && sig[4]<sig[5] && sig[5]<sig[3] && sig[3]<sig[0] && sig[10]<sig[7] && sig[7]<sig[8] && sig[8]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; .... return 0; }
Diese C-Funktion gibt 1 zurück, wenn das Signal mit einem der Muster übereinstimmt, andernfalls gibt sie 0 zurück. Der lange Code scheint darauf hinzudeuten, dass dies nicht der schnellste Weg ist, nach Mustern zu suchen. Es ist besser, einen Ansatz zu verwenden, bei dem die Erkennungsfunktion nicht exportiert werden muss, sondern die Signale nach ihrer Wichtigkeit sortieren und sortieren kann. Ein Beispiel für ein solches System finden Sie
unter dem Link .
Kann Handel zu einem Preis funktionieren? Wie im vorherigen Fall basiert diese Methode nicht auf einem rationalen Finanzmodell. Gleichzeitig versteht jeder, dass wirklich bestimmte Ereignisse auf dem Markt seine Teilnehmer beeinflussen können, wodurch kurzfristige Vorhersagemuster entstehen. Die Anzahl solcher Muster kann jedoch nicht groß sein, wenn Sie nur die Reihenfolge mehrerer aufeinanderfolgender Kerzen in der Tabelle untersuchen. Dann müssen Sie das Ergebnis mit den Daten der Kerzen vergleichen, die nicht in der Nähe sind, sondern im Gegenteil über einen längeren Zeitraum zufällig ausgewählt werden. In diesem Fall erhalten Sie eine nahezu unbegrenzte Anzahl von Mustern - und lösen sich erfolgreich von den Konzepten von Realität und Rationalität. Es ist schwer vorstellbar, wie der zukünftige Preis auf der Grundlage einiger seiner Werte in der letzten Woche vorhergesagt werden kann. Trotzdem arbeiten viele Händler in diese Richtung.
3. Lineare Regression
Eine einfache Basis für viele komplexe Algorithmen für maschinelles Lernen: Vorhersage der Zielvariablen y unter Verwendung einer linearen Kombination von Prädiktoren x1 ... xn.

Gewinnchancen - das ist das Modell. Sie werden berechnet, um die Summe der quadratischen Abweichungen zwischen realen y-Werten, Trainingswerten und vorhergesagtem y gemäß der folgenden Formel zu minimieren:

Bei normalverteilten Stichproben ist eine Minimierung mithilfe von Matrixoperationen möglich, sodass keine Iterationen erforderlich sind. In dem Fall, in dem n = 1 ist - mit nur einem Prädiktor x, wird die Regressionsformel reduziert auf:
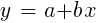
- das heißt, vor einer einfachen linearen Regression und wenn n> 1 ist, ist die lineare Regression multivariant. Auf den meisten Handelsplattformen ist eine einfache lineare Regression verfügbar, beispielsweise der
LinReg- Indikator in TA-Lib. Wenn y = Preis und x = Zeit, kann es als Alternative zu gleitenden Durchschnitten verwendet werden. In der R-Plattform wird eine solche Regression durch die Standardlieferfunktion lm (..) implementiert. Es kann auch durch Polynomregression dargestellt werden. Wie im einfachsten Fall verwenden wir hier eine Vorhersagevariable x, aber auch deren Quadrat und nachfolgende Grade, also xn == xn:
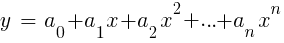
Wenn n = 2 oder n = 3 ist, wird häufig eine Polynomregression verwendet, um den nächsten Durchschnittspreis aus den geglätteten Preisen der letzten Balken vorherzusagen. Für die Polynomregression kann die Polyfit-Funktion von MatLab, R, Zorro und vielen anderen Plattformen verwendet werden.
4. Perceptron
Oft wird es ein neuronales Netzwerk mit nur einem Neuron genannt. Tatsächlich ist das Perzeptron eine Regressionsfunktion, wie oben beschrieben, jedoch mit einem binären Ergebnis, aufgrund dessen es als
logistische Regression bezeichnet wird . Dies ist zwar im Allgemeinen keine Regression, sondern ein Klassifizierungsalgorithmus. Beispielsweise generiert die Beratungsfunktion (PERCEPTRON, ...) des Zorro-Frameworks C-Code, der 100 oder -100 zurückgibt, je nachdem, ob das vorhergesagte Ergebnis ein Schwellenwert ist oder nicht:
int predict(double* sig) { if(-27.99*sig[0] + 1.24*sig[1] - 3.54*sig[2] > -21.50) return 100; else return -100; }
Wie Sie sehen können, entspricht das Sig-Array den Funktionen xn in der Regressionsformel, und die Koeffizienten an sind die digitalen Faktoren.
5. Neuronale Netze
Lineare oder logistische Regression kann nur lineare Probleme lösen. Gleichzeitig passen Handelsaufgaben oft nicht in diese Kategorie. Ein berühmtes Beispiel ist die Vorhersage der Ausgabe einer einfachen XOR-Funktion. Dies beinhaltet auch die Vorhersage des Gewinns aus Transaktionen. Ein künstliches neuronales Netzwerk (ANN) kann nichtlineare Probleme lösen. Dies ist eine Reihe von Perzeptronen, die zu einer Reihe verschiedener Ebenen verbunden sind. Jedes Perzeptron ist ein Netzwerkneuron. Seine Ausgabe wird in andere Neuronen der folgenden Ebene eingegeben:
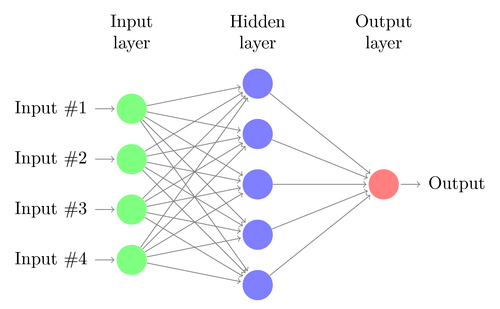
Wie das Perzeptron wird das neuronale Netzwerk trainiert, indem Koeffizienten bestimmt werden, die den Fehler zwischen der Vorhersage und dem Ziel in der Probe minimieren. Dies erfordert einen Approximationsprozess, normalerweise mit der Rückausbreitung des Fehlers von der Ausgabe zur Eingabe mit der Optimierung der Gewichte auf dem Weg. Dieser Prozess hat zwei Einschränkungen. Erstens sollte die Ausgabe von Neuronen eine kontinuierlich differenzierbare Funktion anstelle einer einfachen Schwelle für das Perzeptron sein. Zweitens sollte das Netzwerk nicht sehr tief sein - das Vorhandensein einer großen Anzahl versteckter Ebenen von Neuronen zwischen den Eingabe- und Ausgabedaten schadet nur. Diese zweite Einschränkung begrenzt die Komplexität der Probleme, die ein neuronales Standardnetzwerk lösen kann.
Wenn Sie neuronale Netze zur Vorhersage von Transaktionen verwenden, können Sie viele Parameter manipulieren, die bei ungenauer Ausführung zu einer Auswahlverzerrung (Auswahlverzerrung) führen können:
- Anzahl der versteckten Ebenen;
- die Anzahl der Neuronen in jeder verborgenen Ebene;
- die Anzahl der Backpropagation-Zyklen - Epochen;
- Ausbildungsgrad, Schrittweite der Ära;
- Impuls, Trägheitsfaktor zur Anpassung von Gewichten;
- Aktivierungsfunktion.
Die Aktivierungsfunktion emuliert die Perzeptronschwelle. Für die Rückausbreitung benötigen Sie eine ständig differenzierbare Funktion, die einen weichen Schritt für einen bestimmten Wert von x erzeugt. Typischerweise werden hierfür Sigmoid-, Tanh- oder Softmax-Funktionen verwendet. Manchmal wird eine lineare Funktion verwendet, die die gewichtete Summe aller Eingabedaten zurückgibt. In diesem Fall kann das Netzwerk zur Regression und Vorhersage numerischer Werte anstelle der binären Ausgabe verwendet werden.
Neuronale Netze sind in der Standardpaketlieferung von R (z. B. nnet ist ein Netzwerk mit einer verborgenen Ebene) sowie in vielen anderen Paketen (wie RSNNS und FCNN4R) enthalten.
6. Tiefes Lernen
Deep-Learning-Methoden verwenden neuronale Netze mit vielen verborgenen Ebenen und Tausenden von Neuronen, die mit einfacher Rückausbreitung nicht effektiv trainiert werden können. In den letzten Jahren sind verschiedene Methoden zum Trainieren derart großer Netzwerke populär geworden. Sie beinhalten normalerweise das Vor-Training verborgener Ebenen von Neuronen, um die Effektivität des grundlegenden Lernens zu erhöhen.
Die Restricted Boltzmann Machine (RBM) ist ein unkontrollierter Klassifizierungsalgorithmus mit einer speziellen Netzwerkstruktur, bei der keine Verbindungen zwischen versteckten Neuronen bestehen. Sparse Auto Encoder (SAE) verwendet die übliche Netzwerkstruktur, trainiert jedoch verborgene Pegel auf eine bestimmte Weise vor und reproduziert Eingangssignale auf den Ausgangspegeln mit so wenig aktiven Verbindungen wie möglich. Mit diesen Methoden können Sie sehr komplexe Netzwerke implementieren, um sehr komplexe Lernprobleme zu lösen. Zum Beispiel die Aufgabe, die beste Person zu besiegen, die Go spielt.
Deep-Learning-Netzwerke sind in den Deepnet- und Darch-Paketen für R enthalten. Deepnet enthält den Auto-Encoder und Darch die Boltzmann-Maschine. Unten finden Sie ein Beispiel für Code, der Deepnet mit drei versteckten Ebenen verwendet, um Handelssignale über die neor () -Funktion des Zorro-Frameworks zu verarbeiten:
library('deepnet', quietly = T) library('caret', quietly = T) # called by Zorro for training neural.train = function(model,XY) { XY <- as.matrix(XY) X <- XY[,-ncol(XY)] # predictors Y <- XY[,ncol(XY)] # target Y <- ifelse(Y > 0,1,0) # convert -1..1 to 0..1 Models[[model]] <<- sae.dnn.train(X,Y, hidden = c(50,100,50), activationfun = "tanh", learningrate = 0.5, momentum = 0.5, learningrate_scale = 1.0, output = "sigm", sae_output = "linear", numepochs = 100, batchsize = 100, hidden_dropout = 0, visible_dropout = 0) } # called by Zorro for prediction neural.predict = function(model,X) { if(is.vector(X)) X <- t(X) # transpose horizontal vector return(nn.predict(Models[[model]],X)) } # called by Zorro for saving the models neural.save = function(name) { save(Models,file=name) # save trained models } # called by Zorro for initialization neural.init = function() { set.seed(365) Models <<- vector("list") } # quick OOS test for experimenting with the settings Test = function() { neural.init() XY <<- read.csv('C:/Project/Zorro/Data/signals0.csv',header = F) splits <- nrow(XY)*0.8 XY.tr <<- head(XY,splits) # training set XY.ts <<- tail(XY,-splits) # test set neural.train(1,XY.tr) X <<- XY.ts[,-ncol(XY.ts)] Y <<- XY.ts[,ncol(XY.ts)] Y.ob <<- ifelse(Y > 0,1,0) Y <<- neural.predict(1,X) Y.pr <<- ifelse(Y > 0.5,1,0) confusionMatrix(Y.pr,Y.ob) # display prediction accuracy }
7. Vektoren unterstützen
Wie bei neuronalen Netzen ist die Support-Vektor-Methode eine weitere Erweiterung der linearen Regression. Wenn Sie sich die Regressionsformel noch einmal ansehen:

Dann kann man die Funktionen xn als Koordinaten eines n-dimensionalen Raums interpretieren. Wenn Sie die Zielvariable y auf einen festen Wert setzen, wird die Ebene in diesem Raum bestimmt. Sie wird als Hyperebene bezeichnet, da sie tatsächlich zwei (sogar n-1) Größen hat. Die Hyperebene trennt die Abtastwerte mit y> 0 von denen, bei denen y <0 ist. Die Koeffizienten an können als der Pfad berechnet werden, der die Ebene von den nächsten Abtastwerten trennt - ihren Unterstützungsvektoren, daher der Name des Algorithmus. So erhalten wir einen binären Klassifikator mit der optimalen Trennung von Gewinn- und Verlustproben.
Problem: Normalerweise können diese Stichproben nicht linear geteilt werden - sie werden zufällig in einem Funktionsraum gruppiert. Es ist unmöglich, eine glatte Ebene zwischen den Gewinn- und Verlustoptionen zu ziehen. Wenn dies möglich wäre, könnte man für die Berechnung einfachere Methoden wie die lineare Diskriminanzanalyse verwenden. Im allgemeinen Fall können Sie jedoch den Trick anwenden: Fügen Sie dem Raum weitere Größen hinzu. In diesem Fall kann der Support-Vektor-Algorithmus mehr Parameter mit einer Kernfunktion generieren, die zwei beliebige Prädiktoren kombiniert - ähnlich wie beim Übergang von der einfachen Regression zum Polynom. Je mehr Größen Sie hinzufügen, desto einfacher ist es, die Samples mit einer Hyperebene zu teilen. Dann kann es wieder in den ursprünglichen n-dimensionalen Raum umgewandelt werden.
Referenzvektoren können wie neuronale Netze nicht nur zur Klassifizierung, sondern auch zur Regression verwendet werden. Sie bieten auch eine Reihe von Optionen zur Optimierung und möglichen Umschulung:
- Kernelfunktion - Der RBF-Kernel (radiale Basisfunktion, symmetrischer Kernel) wird normalerweise verwendet, es können jedoch auch andere Kernel ausgewählt werden, z. B. Sigmoid, Polynom und Linear.
- Gamma - RBF Kernbreite.
- Kostenparameter C, „Strafe“ für falsche Klassifizierungen von Trainingsmustern.
Die libsvm-Bibliothek wird häufig verwendet, die im e1071-Paket für R verfügbar ist.
8. Algorithmus der k-nächsten Nachbarn
Im Vergleich zu schwerem ANN und SVM ist dies ein einfacher und angenehmer Algorithmus mit einer einzigartigen Eigenschaft: Er muss nicht trainiert werden. Muster werden das Modell sein. Dieser Algorithmus kann für ein Handelssystem verwendet werden, das ständig durch Hinzufügen neuer Stichproben trainiert wird. Dieser Algorithmus berechnet die Abstände im Funktionsraum vom aktuellen Wert zu den k-nächsten Abtastwerten. Der Abstand im n-dimensionalen Raum zwischen den beiden Mengen (x1 ... xn) und (y1 ... yn) wird nach folgender Formel berechnet:
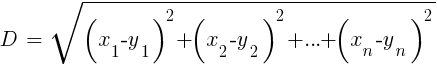
Der Algorithmus sagt das Ziel einfach aus dem Durchschnitt von k Zielvariablen der nächsten Abtastwerte voraus, gewichtet mit ihren Rückgabeabständen. Es kann sowohl für die Klassifizierung als auch für die Regression verwendet werden. Um die nächsten Nachbarn vorherzusagen, können Sie die Funktion knn in R aufrufen oder zu diesem Zweck selbst C-Code schreiben.
9. K-Mittel
Dies ist ein Approximationsalgorithmus für die unkontrollierte Klassifizierung. Es ist dem vorherigen Algorithmus etwas ähnlich. Um Stichproben zu klassifizieren, platziert der Algorithmus zunächst k zufällige Punkte im Funktionsraum. Dann ordnet er einem dieser Punkte alle Proben mit dem geringsten Abstand zu. Dann verschiebt sich der Punkt in die Mitte dieser nächsten Werte. Dies erzeugt neue Probenbindungen, da einige von ihnen jetzt näher an anderen Punkten liegen. Der Vorgang wird wiederholt, bis die erneute Referenzierung infolge der Verschiebung der Punkte aufhört, dh bis jeder Punkt für die nächsten Abtastwerte durchschnittlich ist. Jetzt haben wir k Beispielklassen, die sich jeweils neben einem k-Punkt befinden.
Dieser einfache Algorithmus kann überraschend gute Ergebnisse liefern. In R wird die kmeans-Funktion verwendet, um sie zu implementieren. Ein Beispiel für den Algorithmus finden Sie
hier .
10. Naive Bayes
Dieser Algorithmus verwendet den Bayes'schen Satz zum Klassifizieren von Stichproben nicht numerischer Funktionen (Ereignisse), wie beispielsweise der oben erwähnten Kerzenmuster. Angenommen, Ereignis X (z. B. der Open-Parameter des vorherigen Balkens unter dem Open-Parameter des aktuellen Balkens) wird in 80% der Gewinner-Samples angezeigt. Wie hoch ist dann die Wahrscheinlichkeit, die Stichprobe bei Vorhandensein von Ereignis X zu gewinnen? Dies ist nicht 0,8, wie Sie vielleicht denken. Diese Wahrscheinlichkeit wird nach folgender Formel berechnet:
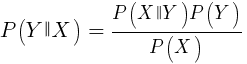
P (Y | X) ist die Wahrscheinlichkeit, dass das Y-Ereignis (Gewinn) in allen Stichproben auftritt, die das X-Ereignis enthalten (in unserem Beispiel Open (1) <Open (0)). In Übereinstimmung mit der Formel ist es gleich der Wahrscheinlichkeit des Auftretens von Ereignis X in allen Gewinnerstichproben (in unserem Fall 0,8), multipliziert mit der Wahrscheinlichkeit Y in allen Stichproben (ungefähr 0,5, wenn Sie die Tipps zum Ausgleichen von Stichproben befolgen) und dividiert durch die Wahrscheinlichkeit des Auftretens von X in alle Proben.
Wenn wir naiv sind und annehmen, dass alle Ereignisse von X unabhängig voneinander sind, können wir die Gesamtwahrscheinlichkeit berechnen, mit der die Stichprobe gewinnt, indem wir einfach die Wahrscheinlichkeiten P (X | gewinnen) für jedes Ereignis X multiplizieren. Dann kommen wir zu der folgenden Formel:
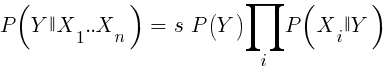
Mit Skalierungsfaktor s. Damit eine Formel funktioniert, müssen Funktionen so ausgewählt werden, dass sie so unabhängig wie möglich sind. Dies wird ein Hindernis für die Verwendung von naiven Bayes für den Handel sein. Beispielsweise sind zwei Ereignisse Schließen (1) <Schließen (0) und Öffnen (1) <Öffnen (0) höchstwahrscheinlich nicht unabhängig voneinander. Numerische Prädiktoren können in Ereignisse umgewandelt werden, indem die Anzahl in separate Bereiche unterteilt wird. Naive Bayes ist im Paket e1071 für R erhältlich.
11. Entscheidungs- und Regressionsbäume
Solche Bäume sagen das Ergebnis numerischer Werte basierend auf einer Entscheidungskette im Ja / Nein-Format in der Struktur von Ästen voraus. Jede Entscheidung repräsentiert das Vorhandensein oder Fehlen von Ereignissen (bei nicht numerischen Werten) oder den Vergleich von Werten mit einem festen Schwellenwert. Eine typische Baumfunktion, die beispielsweise vom Zorro-Framework generiert wird, sieht folgendermaßen aus:
int tree(double* sig) { if(sig[1] <= 12.938) { if(sig[0] <= 0.953) return -70; else { if(sig[2] <= 43) return 25; else { if(sig[3] <= 0.962) return -67; else return 15; } } } else { if(sig[3] <= 0.732) return -71; else { if(sig[1] > 30.61) return 27; else { if(sig[2] > 46) return 80; else return -62; } } } }
Wie wird ein solcher Baum aus einer Reihe von Proben erhalten? Hierfür kann es verschiedene Methoden geben, einschließlich
Shannons Informationsentropie .
Entscheidungsbäume können weit verbreitet sein. Sie eignen sich beispielsweise zur Erzeugung von Vorhersagen, die genauer sind, als sie mit neuronalen Netzen oder Referenzvektoren erzielt werden können. Dies ist jedoch keine universelle Lösung. Der bekannteste Algorithmus dieses Typs ist C5.0, der im C50-Paket für R verfügbar ist.
Um die Qualität der Vorhersagen weiter zu verbessern, können Sie Baumgruppen verwenden, die als zufällige Gesamtstruktur bezeichnet werden. Dieser Algorithmus ist in R-Paketen mit den Namen randomForest, ranger und Rborist verfügbar.
Fazit
Es gibt viele Methoden des Data Mining und des maschinellen Lernens. Die entscheidende Frage lautet hier: Welche sind bessere, modellbasierte oder maschinelle Lernstrategien? Es besteht kein Zweifel, dass maschinelles Lernen eine Reihe von Vorteilen hat. Zum Beispiel müssen Sie sich nicht um die Mikrostruktur des Marktes, die Wirtschaft, kümmern, die Philosophie der Marktteilnehmer oder ähnliche Dinge berücksichtigen. Sie können sich auf reine Mathematik konzentrieren. Maschinelles Lernen ist eine viel elegantere und attraktivere Möglichkeit, Handelssysteme zu erstellen. Auf seiner Seite sind alle Vorteile bis auf einen - zusätzlich zu den Geschichten in den Foren der Händler - der Erfolg dieser Methode im realen Handel schwer nachzuvollziehen.
Fast jede Woche werden neue Artikel über den Handel mit maschinellem Lernen veröffentlicht. Solche Materialien sollten mit einer gewissen Skepsis aufgenommen werden. Einige Autoren behaupten fantastische Gewinnraten von 70%, 80% oder sogar 85%. Allerdings sagen nur wenige, dass Sie Geld verlieren können, selbst wenn die Vorhersagen gewinnen. Eine Genauigkeit von 85% führt normalerweise zu einem Rentabilitätsindikator über 5 - wenn alles so einfach wäre, würden die Entwickler eines solchen Systems bereits zu Milliardären. Aus irgendeinem Grund schlägt es jedoch fehl, dieselben Ergebnisse einfach durch Wiederholen der in den Artikeln beschriebenen Methoden zu reproduzieren.
Im Vergleich zu modellbasierten Systemen gibt es nur sehr wenige wirklich erfolgreiche maschinelle Lernsysteme. Beispielsweise werden sie von erfolgreichen Hedgefonds selten eingesetzt. Vielleicht wird sich in Zukunft etwas ändern, wenn die Rechenleistung noch zugänglicher wird, aber Deep-Learning-Algorithmen bleiben für Geeks vorerst ein interessanteres Hobby als ein echtes Geldverdienungsinstrument an der Börse.
Sonstige finanz- und börsenbezogene Materialien von ITI Capital :