Um Einsteins Gleichungen zu überprüfen, müssen Sie ein Schwarzes Loch treten

Zwei Forscherteams haben bedeutende Fortschritte beim Nachweis der Hypothese der Stabilität von Schwarzen Löchern erzielt, dem wichtigsten mathematischen Test von Einsteins allgemeiner Relativitätstheorie.

Im November 1915 beschrieb Albert Einstein in einem Vortrag an der Preußischen Akademie der Wissenschaften eine Idee, die die Menschheit um das Universum drehte. Anstatt die Geometrie von Raum und Zeit festzuhalten, erklärte Einstein, dass wir in einer vierdimensionalen Realität leben, die Raumzeit genannt wird und deren Form als Reaktion auf Materie und Energie schwankt.

Einstein beschrieb diese wichtige Idee ausführlich in mehreren Gleichungen, die als „ Einstein-Gleichungen “ (oder Gleichungen des Gravitationsfeldes) bezeichnet werden und den Kern seiner GTR bilden. Diese Theorie wurde durch alle experimentellen Tests bestätigt, denen sie im nächsten Jahrhundert unterzogen wurde.

Und obwohl Einsteins Theorie die beobachtete Welt zu beschreiben scheint, bleibt die zugrunde liegende Mathematik weitgehend rätselhaft. Mathematiker konnten nur sehr wenige Beweise für die Gleichungen selbst liefern. Wir wissen, dass sie funktionieren, aber wir können nicht genau sagen, warum. Sogar Einstein musste zu Annäherungen und nicht zu exakten Lösungen zurückkehren, um das Universum durch die von ihm geschaffenen Linsen zu sehen.

Aber im vergangenen Jahr haben Mathematiker die GR-Mathematik klarer in den Fokus gerückt. Zwei Gruppen entwickelten Lösungen für ein wichtiges Problem in GR, das als Stabilitätshypothese für das Schwarze Loch bekannt ist. Ihre Arbeit beweist, dass Einsteins Gleichungen der physischen Intuition für das Verhalten der Raumzeit entsprechen: Wenn Sie eine scharfe Störung anwenden, erschrickt sie wie Gelee und beruhigt sich dann in einem stabilen Zustand, von dem aus alles begann.

„Wenn die Entscheidungen instabil wären, würde dies bedeuten, dass sie nicht physisch sind. Es wäre ein mathematischer Geist, der in der Mathematik existiert, aber aus physikalischer Sicht keine Rolle spielt “, sagte Sergiu Kleinerman , Mathematiker an der Princeton University, und der Autor zusammen mit Jeremy Szeftel eines von zwei Ergebnissen .

Um die Beweise zu vervollständigen, mussten Mathematiker die grundlegende Komplexität von Einsteins Gleichungen lösen. Um die Entwicklung der Raum-Zeit-Form zu beschreiben, benötigen Sie ein Koordinatensystem - etwa Längen- und Breitengrade -, das Ihnen sagt, wo sich einige Punkte befinden. Und in der Raumzeit ist es sehr schwierig, ein Koordinatensystem zu finden, das überall funktioniert.

Schüttle das Schwarze Loch

Wie Sie wissen, beschreibt GR die Raumzeit als eine Art Gummiplatte. In Abwesenheit von Materie ist das Blatt flach. Lassen Sie Bälle darauf fallen - Sterne und Planeten - und das Blatt verformt sich. Kugeln rollen aufeinander zu. Wenn sich Objekte bewegen, ändert sich auch die Form der Gummiplatte als Reaktion.

Einsteins Gleichungen beschreiben die Entwicklung der Raum-Zeit-Form. Sie geben ihnen Informationen über die Krümmung und Energie an jedem Punkt und sie geben die Form der Raum-Zeit in der Zukunft an. In diesem Sinne ähneln Einsteins Gleichungen allen Gleichungen, die ein physikalisches Phänomen simulieren: Hier ist der Ball zum Zeitpunkt Null und hier - nach fünf Sekunden.

"Dies ist eine mathematisch genaue quantitative Version der Behauptung, dass Raum-Zeit in Gegenwart von Materie gekrümmt ist", sagte Peter Hinz, ein wissenschaftlicher Mitarbeiter am Clay Institute of Mathematics der University of California in Berkeley, der mit Andras Vasya für das zweite Ergebnis verantwortlich ist.

Fast unmittelbar nach der Veröffentlichung der GTR fand der deutsche Physiker Karl Schwarzschild 1916 eine genaue Lösung für die Gleichungen, die das beschreiben, was wir heute unter dem Namen eines Schwarzen Lochs kennen (dieser Begriff erschien nur fünf Jahrzehnte später ). Später fanden Physiker genaue Lösungen, die ein rotierendes Schwarzes Loch und BH mit elektrischer Ladung beschreiben.

Und das sind alles genaue Entscheidungen, die BH beschreiben. Wenn Sie mindestens ein zweites BH hinzufügen, wird das Zusammenspiel von Kräften für die moderne Mathematik so kompliziert, dass es nur in ganz besonderen Fällen damit fertig wird.

Wir können jedoch noch wichtige Fragen zu dieser begrenzten Gruppe von Lösungen stellen. Eine solche Frage stellte sich 1952 aufgrund der Arbeit der französischen Mathematikerin Yvonne Choquet-Bruhat. Tatsächlich klingt es so: Was passiert, wenn Sie ein Schwarzes Loch schütteln?


Wenn Sie das BH schütteln, entstehen Gravitationswellen. Der Nachweis der Stabilitätshypothese ist der gleiche wie der Beweis, dass diese Wellen wie Wellen auf der Oberfläche eines Teiches nach dem Fall eines Steins in die Leere streuen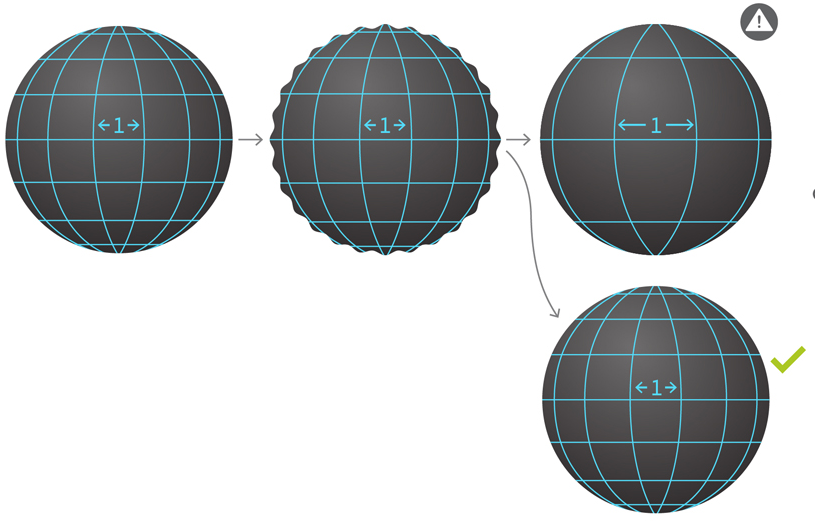


Die Raumzeit ändert sich mit der Zeit, und das zur Messung gedämpfter Wellen verwendete Gitter ändert sich damit. Die Vorlage bestimmt die Änderungen am Raster und muss korrekt ausgewählt werden. Angenommen, wir haben eine Raumzeit mit einem 1-cm-Gitter, das einem bestimmten Muster zugeordnet ist. Wir werden die Raumzeit stören, so dass Gravitationswellen auftreten. Ein falsch ausgewähltes Muster kann dazu führen, dass sich die Gitterabstände ändern, und es sieht so aus, als würden sich die Wellen nicht abschwächen. Das richtige Muster ist entscheidend für die Messung der Rückkehr zur Nachhaltigkeit.

Dieses Problem ist als BH-Stabilitätshypothese bekannt. Sie sagt voraus, dass Lösungen für Einsteins Gleichungen "unter Störungen stabil" sein werden. Informell gesehen wird der Raum, wenn Sie den BH schockieren, zuerst auch teurer, und dann wird er sich in Toga in einer Form beruhigen, die dem sehr ähnlich sieht, mit dem wir begonnen haben. „Nachhaltigkeit bedeutet grob gesagt, dass die endgültige Dynamik der ursprünglichen Lösung sehr nahe kommt, wenn wir spezielle Lösungen nehmen und sie ein wenig empören und die Daten ändern“, sagte Kleinerman.

Die sogenannte „Stabilität“ ist ein wichtiger Test für jede physikalische Theorie. Um dies zu verstehen, wäre es nützlich, ein Beispiel vorzustellen, das vertrauter ist als BH.

Stellen Sie sich einen Teich vor. Stellen Sie sich nun vor, Sie hätten seine Oberfläche empört, indem Sie dort einen Stein geworfen haben. Der Teich ist ein wenig aufgeregt, und dann wird er sich beruhigen. Mathematisch sollten die Lösungen der Gleichungen, die zur Beschreibung des Teichs verwendet werden (in diesem Fall die Navier-Stokes-Gleichungen ), dieses physikalische Grundbild beschreiben. Wenn die ursprüngliche Lösung in ferner Zukunft nicht mit der Entscheidung übereinstimmt, fragen Sie sich möglicherweise, ob Ihre Gleichungen korrekt sind.

"Eine Gleichung kann beliebige Eigenschaften haben, sie kann mathematisch korrekt sein, aber wenn sie den physikalischen Erwartungen widerspricht, kann sie nicht korrekt sein", sagte Vasya.


Peter Hinz, Mathematiker an der Universität von Kalifornien

Für Mathematiker, die an Einsteins Gleichungen arbeiten, war der Nachweis der Stabilität noch schwieriger zu finden als Lösungen für die Gleichungen selbst. Betrachten Sie den Fall eines flachen Minkowski-Raums - der einfachsten aller Raum-Zeit-Konfigurationen. Diese Lösung von Einsteins Gleichungen wurde 1908 im Kontext von Einsteins früherer spezieller Relativitätstheorie entdeckt. Aber erst 1993 konnten Mathematiker beweisen, dass man, wenn man die flache, leere Raumzeit schüttelt, wieder die flache und leere Raumzeit bekommt. Dieses von Kleinermann und Demetrios Christodoulou erzielte Ergebnis ist eine verehrte Arbeit auf diesem Gebiet.

Eine der Hauptschwierigkeiten beim Nachweis der Stabilität besteht darin, zu verfolgen, was in der vierdimensionalen Raumzeit während der Entwicklung einer Lösung geschieht. Sie benötigen ein Koordinatensystem, mit dem Sie Entfernungen messen und Punkte in der Raumzeit bestimmen können, z. B. die Längen- und Breitengrade, mit denen Sie einen Ort auf der Erde bestimmen. Es ist jedoch nicht einfach, ein Koordinatensystem zu finden, das zu jedem Zeitpunkt im Raum funktioniert und weiterhin funktioniert, wenn sich die Form der Raumzeit ändert.

"Wir kennen keinen Weg, der für alle Fälle geeignet ist", sagte Hinz in einer E-Mail. "Das Universum gibt uns kein bevorzugtes Koordinatensystem."

Messproblem

Das erste, was man über Koordinatensysteme verstehen muss, ist, dass die Leute sie erfunden haben. Das zweite - nicht jedes Koordinatensystem ermöglicht es Ihnen, alle Punkte im Raum zu definieren.

Nehmen Sie Längen- und Breitengrad: Sie können beliebig zugewiesen werden. Kartographen konnten jede imaginäre Linie als Nullmeridian wählen. Und obwohl Breiten- und Längengrade dazu beitragen, fast jeden Ort auf der Erde zu bestimmen, sind sie am Nord- und Südpol nicht mehr sinnvoll. Wenn Sie nichts über die Erde wussten und nur Längen- und Breitengrade an Ihren Händen hatten, können Sie fälschlicherweise den Schluss ziehen, dass an diesen Punkten etwas topologisch Falsches passiert.

Diese Möglichkeit, aufgrund der Unzulänglichkeit des Koordinatensystems, das ihn beschreibt, falsche Schlussfolgerungen über die Eigenschaften des physikalischen Raums zu ziehen, ist der Grund dafür, warum es so schwierig ist, die Stabilität der Raumzeit zu beweisen.

"Es mag sein, dass Stabilität existiert, aber wir verwenden instabile Koordinaten und überspringen damit die Wahrheit der Stabilität", sagte Michalis Dafermos, Mathematiker an der Universität von Cambridge, ein führender Spezialist für das Studium von Einsteins Gleichungen.

Im Kontext der Theorie der Stabilität eines Schwarzen Lochs sollte sich jedes verwendete Koordinatensystem auf die gleiche Weise entwickeln wie die Form der Raumzeit - so wie sich ein bequemer Handschuh an die Veränderung der Handform anpasst. Die Entsprechung zwischen dem Koordinatensystem und der Raumzeit sollte am Anfang gut sein und den ganzen Weg gut bleiben. Ist dies nicht der Fall, können zwei Dinge passieren, die den Versuch beeinträchtigen, die Existenz von Stabilität zu beweisen.


Sergiu Kleinerman, Mathematiker an der Princeton University

Erstens kann Ihr Koordinatensystem somit die Form ändern, die an bestimmten Punkten bricht, genau wie Breiten- und Längengrade an den Polen nicht mehr funktionieren. Solche Punkte werden als "Koordinatensingularitäten" bezeichnet (um sie von physikalischen Singularitäten, beispielsweise Schwarzen Löchern, zu unterscheiden). Dies sind unbestimmte Punkte im Koordinatensystem, die es nicht ermöglichen, die Entwicklung der Lösung bis zum Ende vollständig zu beschreiben.

Zweitens kann ein schlecht ausgewähltes Koordinatensystem das sehr physikalische Phänomen verbergen, das es messen sollte. Um zu beweisen, dass Lösungen von Einsteins Gleichungen nach Störungen einen ruhigen Zustand erreichen, müssen Mathematiker die durch Störungen verursachten Wellen der Raum-Zeit sorgfältig überwachen. Um zu verstehen, warum dies notwendig ist, lohnt es sich, noch einmal auf die Analogie mit dem Teich zurückzukommen. Ein Stein, der in einen Teich geworfen wird, erzeugt Wellen. Die Langzeitstabilität des Teiches beruht auf der Tatsache, dass die Wellen mit der Zeit schwächer werden - sie werden immer kleiner, bis keine Spur ihrer Anwesenheit mehr vorhanden ist.

Die Situation ist ähnlich wie in der Raumzeit. Die Störung verursacht eine Kaskade von Gravitationswellen, und um die Stabilität zu beweisen, muss nachgewiesen werden, dass diese Wellen gedämpft sind. Dazu wird ein Koordinatensystem oder „Gitter“ benötigt, um die Größe der Wellen zu messen. Mit dem richtigen Raster können Mathematiker sehen, wie sich die Wellen abflachen und schließlich für immer verschwinden.

"Die Dämpfung muss relativ zu etwas gemessen werden, und hier kommt das Netzproblem ins Spiel", sagte Kleinerman. "Wenn wir das falsche Gitter nehmen, kann dies nicht bewiesen werden, selbst wenn Stabilität vorhanden ist, da das Gitter mir keine Dämpfung zeigt." Und wenn Sie die Dämpfungsrate der Wellen nicht berechnen, ist es unmöglich, Stabilität zu beweisen. "

Das Problem ist, dass das Koordinatensystem zwar äußerst wichtig ist, es jedoch nicht offensichtlich ist, welches System gewählt werden soll. "Es gibt zu viel Freiheit bei der Auswahl der Bedingungen für dieses Raster", sagte Hinz. "Und die meisten Optionen werden sich als falsch herausstellen."

Auf dem Weg zum Ziel

Ein vollständiger Beweis für die Stabilität von Schwarzen Löchern erfordert den Nachweis, dass alle bekannten Lösungen der Einstein-Gleichungen für BHs (mit dem Spin des Schwarzen Lochs innerhalb bestimmter Grenzen) nach einer Störung stabil sind. Zu den bekannten Lösungen gehören die Schwarzschild-Lösung, die die Raumzeit eines nicht rotierenden BH beschreibt, und die Kerr-Lösungsfamilie, die die Raum-Zeit-Konfiguration beschreibt, in der es nur ein rotierendes BH gibt (und die Eigenschaften dieses BH - Masse und Drehimpuls - unterscheiden sich innerhalb der Lösungsfamilie). .

Beide neuen Ergebnisse haben sich teilweise zum Beweis einer vollständigen Hypothese entwickelt.

Hinz und Washi haben in einem 2016 auf arxiv.org veröffentlichten Artikel bewiesen, dass langsam rotierende Schwarze Löcher stabil sind. Ihre Arbeit umfasst jedoch nicht BHs, die sich mit einer Geschwindigkeit drehen, die über einer bestimmten Schwelle liegt.

Ihre Beweise haben auch mehrere Annahmen über die Natur der Raumzeit. Die ursprüngliche Hypothese fand im Minkowski-Raum statt, der nicht nur flach und leer ist, sondern auch eine bestimmte Größe hat. Der Beweis von Hintz und Vasya findet im de Sitter-Raum statt, wo die Raumzeit mit Beschleunigung nach außen wächst, wie im realen Universum. Das Ändern der Szene vereinfacht das Problem aus technischer Sicht, und dies kann analog verstanden werden: Wenn Sie einen Stein in einen expandierenden Teich werfen, wird die Expansion die Wellen dehnen und sie werden schneller schwächer als wenn sich der Teich nicht ausdehnt.

"Wir betrachten ein Universum mit beschleunigter Expansion", sagte Hinz. "Es macht die Aufgabe ein wenig einfacher, weil dieser Prozess die Gravitationswellen verdünnt."

Kleinermann und Scheftel haben ein etwas anderes Merkmal. Ihr Beweis, dessen erster Teil im vergangenen November veröffentlicht wurde, findet in der Schwarzschild-Raumzeit statt - was näher an der ursprünglichen, komplexeren Bedingung des Problems liegt. Sie beweisen die Stabilität eines nicht rotierenden BH, betreffen jedoch nicht die Entscheidungen, in denen es rotiert. Darüber hinaus beweisen sie die BH-Stabilität nur für eine enge Klasse von Störungen - diejenigen, bei denen die erzeugten Gravitationswellen in gewisser Weise symmetrisch sind.

Beide Ergebnisse präsentieren neue Techniken zur Auswahl des geeigneten Koordinatensystems. Hinz und Vasi beginnen mit einer ungefähren Lösung von Gleichungen, die auf einem ungefähren Koordinatensystem basieren, und erhöhen schrittweise die Genauigkeit der Antwort, bis sie zu exakten Lösungen und gut verhaltenen Koordinaten kommen. Kleinerman und Scheftel verfolgen einen geometrischeren Ansatz.

Jetzt versuchen die beiden Teams, anhand ihrer Methoden einen Beweis für die vollständige Hypothese zu erstellen. Einige Beobachter-Experten glauben, dass der Tag, an dem es funktioniert, nicht mehr weit ist.

"Ich glaube wirklich, dass sich jetzt alles in einem Stadium technischer Schwierigkeiten befindet", sagte Dafermos. "Es stellt sich heraus, dass zur Lösung dieses Problems keine neuen Ideen mehr erforderlich sind." Er betonte, dass der endgültige Beweis von jedem der Mathematiker erbracht werden kann, die derzeit an dem Problem arbeiten.

Einsteins Gleichungen dienten hundert Jahre lang als zuverlässige experimentelle Anweisung an das Universum. Jetzt nähern sich Mathematiker wahrscheinlich der Demonstration, warum sie so gut funktionieren.