Bestimmung der Gasdichte aus den Ergebnissen der Druck- und Temperaturmessung mit Arduino-Sensoren

Einführung

Die Aufgabe, die Parameter eines Gasgemisches zu messen, ist in Industrie und Handel weit verbreitet. Das Problem, verlässliche Informationen zu erhalten, wenn die Parameter des Zustands des gasförmigen Mediums und seiner Eigenschaften mit technischen Mitteln gemessen werden, wird durch die in den Normen (MVI) festgelegten Messverfahren gelöst, beispielsweise wenn die Durchflussrate und die Menge der Gase mit Standardverengungsvorrichtungen [1] oder mit einer Turbine gemessen werden. Rotations- und Wirbel-Durchflussmesser und -Zähler [2].

Die periodische Gasanalyse ermöglicht es uns, eine Entsprechung zwischen dem tatsächlich analysierten Gemisch und seinem Modell herzustellen, nach der die physikochemischen Parameter des Gases im MVI berücksichtigt werden: die Zusammensetzung des Gasgemisches und die Gasdichte unter Standardbedingungen.
Das MVI berücksichtigt auch die thermophysikalischen Eigenschaften des Gases: Dichte unter Betriebsbedingungen (Druck und Temperatur des Gases, bei dem seine Durchflussrate oder sein Volumen gemessen wird), Viskosität, Faktor und Kompressibilitätsfaktor.

Die in Echtzeit gemessenen Gaszustandsparameter umfassen: Druck (Differenzdruck), Temperatur, Dichte. Zur Messung dieser Parameter werden jeweils Messmittel verwendet: Manometer (Differenzdruckmesser), Thermometer, Densitometer. Die Messung der Dichte des gasförmigen Mediums kann durch direkte oder indirekte Messmethoden gemessen werden. Die Ergebnisse sowohl direkter als auch indirekter Messmethoden hängen vom Fehler der Messgeräte und vom methodischen Fehler ab. Unter Betriebsbedingungen können die Messinformationssignale durch signifikantes Rauschen beeinflusst werden, dessen mittlere quadratische Abweichung den Instrumentenfehler überschreiten kann. In diesem Fall ist die dringende Filterung von Messinformationssignalen eine dringende Aufgabe.

Dieser Artikel beschreibt die Methode zur indirekten Messung der Gasdichte unter Betriebs- und Standardbedingungen unter Verwendung eines Kalman-Filters.

Mathematisches Modell zur Bestimmung der Gasdichte

Wenden wir uns den Klassikern zu und erinnern uns an die Zustandsgleichung eines idealen Gases [3]. Wir haben:

1. Die Mendeleev-Clapeyron-Gleichung: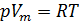

(1)

wo:

- Gasdruck;

- Molvolumen;

R ist die universelle Gaskonstante,

;;

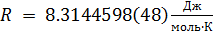
T ist die absolute Temperatur, T = 273,16 K.

2. Zwei gemessene Parameter:

p - Gasdruck, Pa
t ist die Gastemperatur ° C.

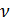
Es ist bekannt, dass das Molvolumen hängt vom Gasvolumen V und der Anzahl der Mol Gas ab in diesem Band:

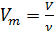
(2)

Es ist auch bekannt, dass

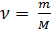
(3)

wobei: m die Masse des Gases ist, M die Molmasse des Gases ist.

Mit (2) und (3) schreiben wir (1) in der Form um:

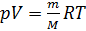
(4).

Bekanntlich ist die Dichte einer Substanz

ist gleich:

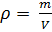
(5).

Aus (4) und (5) leiten wir die Gleichung für die Gasdichte ab

::

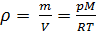
(6)

und geben Sie die Notation für den Parameter ein

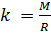
, die von der Molmasse des Gasgemisches abhängt:

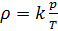
(7).

Wenn sich die Zusammensetzung des Gasgemisches nicht ändert, ist der Parameter k konstant.
Um die Dichte des Gases zu berechnen, ist es notwendig, die Molmasse des Gasgemisches zu berechnen.

Die Molmasse eines Stoffgemisches ist definiert als das arithmetische Mittel der Molmasse der Massenanteile, die im Gemisch einzelner Substanzen enthalten sind.

Wir nehmen die bekannte Zusammensetzung von Substanzen in einem Gasgemisch - in Luft, die besteht aus:

• 23 Gew .-% Sauerstoffmoleküle
• 76 Gew .-% Stickstoffmoleküle
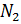
• 1 Gew .-% Argonatome

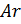
Die Molmassen dieser Luftsubstanzen sind jeweils gleich:

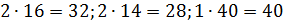
g / mol.

Wir berechnen die Molmasse der Luft als gewichteten arithmetischen Durchschnitt:



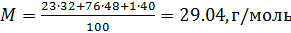
Jetzt den Wert der Konstante kennen

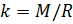
können wir die Luftdichte nach der Formel (7) unter Berücksichtigung der Messwerte berechnen

und t :

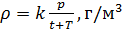
Bringen Sie die Gasdichte auf normale Standardbedingungen

In der Praxis werden Messungen der Eigenschaften von Gasen unter verschiedenen physikalischen Bedingungen durchgeführt. Um einen Vergleich zwischen verschiedenen Datensätzen zu gewährleisten, müssen Standardbedingungen festgelegt werden [4].

Standardbedingungen für Temperatur und Druck sind die in der Norm festgelegten physikalischen Bedingungen, mit denen die Eigenschaften von Substanzen korrelieren, die von diesen Bedingungen abhängen.

Verschiedene Organisationen legen ihre Standardbedingungen fest, zum Beispiel: Die Internationale Union für reine und angewandte Chemie (IUPAC) hat die Definition von Standardtemperatur und -druck (STP) im Bereich der Chemie festgelegt: Temperatur 0 ° C (273,15 K), Absolutdruck 1 bar (Pa); Das Nationale Institut für Standards und Technologie (NIST) legt eine Temperatur von 20 ° C (293,15 K) und einen absoluten Druck von 1 atm (101,325 kPa) fest. Diese Norm wird als normale Temperatur und normaler Druck (NTP) bezeichnet. Die Internationale Organisation für Normung (ISO) legt Standardbedingungen für Erdgas fest (ISO 13443: 1996, bestätigt 2013): Temperatur 15,00 ° C und absoluter Druck 101,325 kPa.

In Industrie und Handel ist es daher erforderlich, Standardbedingungen für Temperatur und Druck anzugeben, für die die erforderlichen Berechnungen durchgeführt werden.

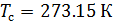
Wir berechnen die Luftdichte gemäß Gleichung (8) unter Betriebsbedingungen von Temperatur und Druck. In Übereinstimmung mit (6) schreiben wir die Gleichung für die Luftdichte unter Standardbedingungen: Temperatur und absoluter Druck ::

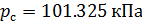
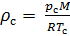
(9).

Wir machen die Berechnung der Luftdichte auf Standardbedingungen reduziert. Wir teilen Gleichung (9) durch Gleichung (6) und schreiben diese Beziehung für ::

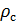
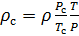
(10).

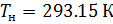
In ähnlicher Weise erhalten wir eine Gleichung zur Berechnung der Luftdichte, die auf normale Bedingungen reduziert ist: Temperatur und absoluter Druck

::

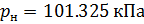
(11).

In den Gleichungen (10) und (11) verwenden wir die Werte der Luftparameter , T und P aus Gleichung (8), erhalten unter Betriebsbedingungen.

Die Implementierung des Messkanaldrucks und der Temperatur

Um viele Probleme beim Erhalten von Informationen in Abhängigkeit von ihrer Komplexität zu lösen, ist es zweckmäßig, einen Prototyp eines zukünftigen Systems zu erstellen, das auf einer der Mikrocontroller-Plattformen wie Arduino, Nucleo, Teensy usw. basiert.

Was könnte einfacher sein? Lassen Sie uns eine Mikrocontroller-Plattform zur Lösung eines bestimmten Problems erstellen - ein System zur Messung von Druck und Temperatur erstellen, möglicherweise weniger Geld ausgeben und alle Vorteile der Softwareentwicklung in der Arduino Software (IDE) -Umgebung nutzen.

Dafür benötigen wir auf Hardwareebene Komponenten:

1. Arduino (Uno, ...) - Verwendung als Programmierer;
2. Mikrocontroller ATmega328P-PU - Mikrocontroller der zukünftigen Plattform;
3. einen 16-MHz-Quarzresonator und ein Paar Keramikkondensatoren mit jeweils 12-22 pF (gemäß den Empfehlungen des Herstellers);
4. eine Takttaste zum Zurücksetzen des Mikrocontrollers und ein Pull-up plus Strom zum RESET-Pin des 1 kOhm-Widerstands des Mikrocontrollers;
5. BMP180 - Temperatur- und Druckmessumformer mit I2C-Schnittstelle;
6. Schnittstellenkonverter TTL / USB;
7. Verbrauchsmaterialien - Drähte, Lötmittel, Leiterplatten usw.

Ein schematisches Diagramm der Plattform unter Berücksichtigung der erforderlichen Schnittstellen: Eine serielle Standardschnittstelle, I2C und nichts weiter, ist in Abb. 1 dargestellt. 1.


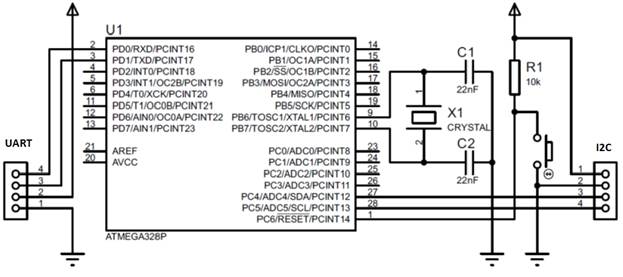Abb. 1 - Schematische Darstellung einer Mikrocontroller-Plattform zur Implementierung eines Druck- und Temperaturmesssystems

Nun werden wir die Phasen der Umsetzung unserer Aufgabe betrachten.

1. Zuerst brauchen wir einen Programmierer. Wir verbinden Arduino (Uno, ...) mit dem Computer. Gehen Sie in der Arduno Software-Umgebung im Menü zu Datei-> Beispiele-> 11. ArdunoISP kommen wir zum Programmierer Programmierer ArduinoISP, den wir in Arduino nähen. Wählen Sie zunächst im Menü Extras die Karte, den Prozessor, den Lader und den Port aus. Nach dem Herunterladen des ArduinoISP- Programms auf das Board verwandelt sich unser Arduino in einen Programmierer und ist für den vorgesehenen Zweck einsatzbereit. Wählen Sie dazu in der Arduno Software-Umgebung im Menü Extras den Eintrag Programmierer: „Arduino als ISP “.

2. Verbinden Sie den Slave-Mikrocontroller ATmega328P über die SPI- Schnittstelle mit dem Arduino-Master-Programmierer (Uno, ...), Abb. 2. Es ist zu beachten, dass zuvor die Bits des Low Fuse Byte-Registers des ATmega328P-Mikrocontrollers in einen nicht programmierten Zustand versetzt wurden. Gehen Sie zur Arduno Software-Umgebung und wählen Sie im Menü Extras den Eintrag Burn Loader . Flashen des ATmega328P-Mikrocontrollers.


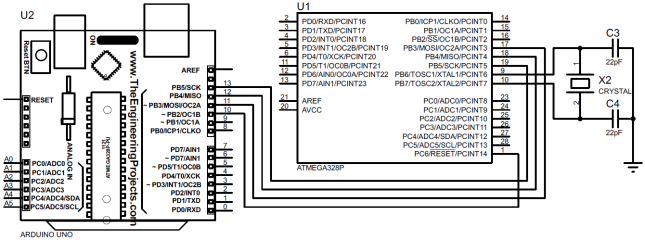Abb. 2 - Anschlussplan des Mikrocontrollers an den Programmierer

3. Nach erfolgreicher Firmware kann der ATmega328P-Mikrocontroller auf der entwickelten Mikrocontroller-Plattform (Abb. 3) installiert werden, die sowohl programmierbar ist als auch auf dem vollwertigen Arduino (Uno, ...). Das Abrufprogramm für den Druck- und Temperaturmessumformer ist in Listing 1 dargestellt.


Abb. 3 Druck- und Temperaturmesssystem

Python-Programm zum Filtern nach Temperatur- und Druckkanälen und zum Erhalten von Ergebnissen

Das Python-Programm für die Methode zur Bestimmung der Gasdichte aus Druck- und Temperaturmessungen ist in Listing 2 dargestellt. Informationen aus dem Messsystem werden in Echtzeit angezeigt.


Die Berechnungsergebnisse werden durch Auflistung und Abb. 4, 5, 6.



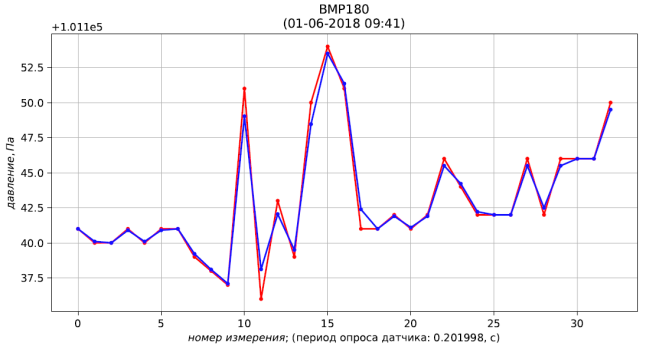Abb. 4 - Messergebnisse (rot) und Filtration (blau) des Drucks


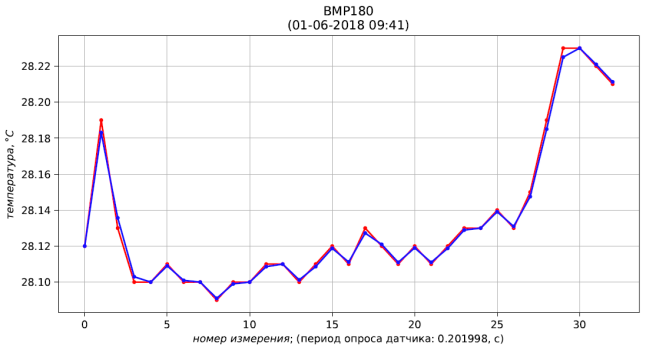Abb. 5 - Messergebnisse (rot) und Filtration (blau) der Temperatur


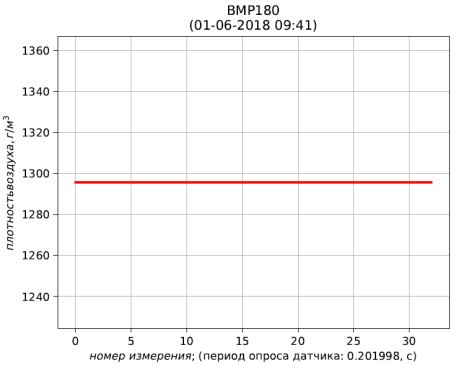Abb. 6 - Berechnungsergebnisse der auf Standardbedingungen reduzierten Luftdichte (Temperatur 273,15 K; absoluter Druck 101,325 kPa)

Schlussfolgerungen

Es wurde eine Technik zur Bestimmung der Gasdichte aus Druck- und Temperaturmessungen unter Verwendung von Arduino-Sensoren und Python-Software entwickelt.

Links zu Informationsquellen

1. GOST 8.586.5-2005. URL
2. GOST R 8.740 - 2011. URL
3. Ideales Gasgesetz. URL
4. Standardbedingungen für Temperatur und Druck. URL