Wie Maschinen Big Data analysieren: Eine Einführung in Clustering-Algorithmen

Übersetzung, wie Maschinen Big Data verstehen: eine Einführung in Clustering-Algorithmen .

Schauen Sie sich das Bild unten an. Dies ist eine Sammlung von Insekten (Schnecken sind keine Insekten, aber wir werden keinen Fehler finden) in verschiedenen Formen und Größen. Teilen Sie sie nun nach dem Grad der Ähnlichkeit in mehrere Gruppen ein. Kein Fang. Beginnen Sie mit der Gruppierung von Spinnen.



Fertig? Obwohl es hier keine „richtige“ Lösung gibt, müssen Sie diese Kreaturen in vier Cluster unterteilt haben . In einer Gruppe gibt es Spinnen, in der zweiten - ein Paar Schnecken, in der dritten - Schmetterlinge und in der vierten - ein Trio von Bienen und Wespen.

Gut gemacht, richtig? Sie könnten wahrscheinlich dasselbe tun, wenn doppelt so viele Insekten auf dem Bild wären. Und wenn Sie viel Zeit gehabt hätten - oder ein Verlangen nach Entomologie -, hätten Sie wahrscheinlich Hunderte von Insekten gruppiert.

Für eine Maschine ist es jedoch keine leichte Aufgabe, zehn Objekte in sinnvolle Cluster zu gruppieren. Dank eines so komplexen Zweigs der Mathematik wie der Kombinatorik wissen wir, dass 10 Insekten auf 115.975 Arten gruppiert sind. Und wenn es 20 Insekten gibt, wird die Anzahl der Clustering-Optionen 50 Billionen überschreiten .

Mit hundert Insekten ist die Anzahl der möglichen Lösungen größer als die Anzahl der Elementarteilchen im bekannten Universum . Wie viel mehr? Nach meinen Schätzungen etwa fünfhundert Millionen Milliarden Mal mehr . Es stellt sich heraus, dass mehr als vier Millionen Milliarden Google- Lösungen ( was ist Google? ). Und das nur für Hunderte von Objekten.

Fast alle diese Kombinationen sind bedeutungslos. Trotz der unvorstellbaren Anzahl von Lösungen haben Sie selbst sehr schnell eine der wenigen nützlichen Möglichkeiten zum Clustering gefunden.

Wir Menschen halten unsere hervorragende Fähigkeit, große Datenmengen zu katalogisieren und zu verstehen, für selbstverständlich. Es spielt keine Rolle, ob es sich um Text, Bilder auf dem Bildschirm oder eine Folge von Objekten handelt - Menschen verstehen im Allgemeinen die Daten aus der Umgebung effektiv.

Wie kann ich die Arbeitseffizienz verbessern, da ein Schlüsselaspekt der KI-Entwicklung und des maschinellen Lernens darin besteht, dass Maschinen große Mengen an Eingabedaten schnell verstehen können? In diesem Artikel werden drei Clustering-Algorithmen betrachtet, mit denen Maschinen große Datenmengen schnell erfassen können. Diese Liste ist bei weitem nicht vollständig - es gibt andere Algorithmen - aber es ist bereits durchaus möglich, damit zu beginnen.

Für jeden Algorithmus werde ich beschreiben, wann er verwendet werden kann, wie er funktioniert, und ich werde auch ein Beispiel mit schrittweiser Analyse geben. Ich glaube, für ein wirkliches Verständnis des Algorithmus müssen Sie seine Arbeit selbst wiederholen. Wenn Sie wirklich interessiert sind , werden Sie feststellen, dass es am besten ist, Algorithmen auf Papier auszuführen. Handeln Sie, niemand wird Ihnen die Schuld geben!


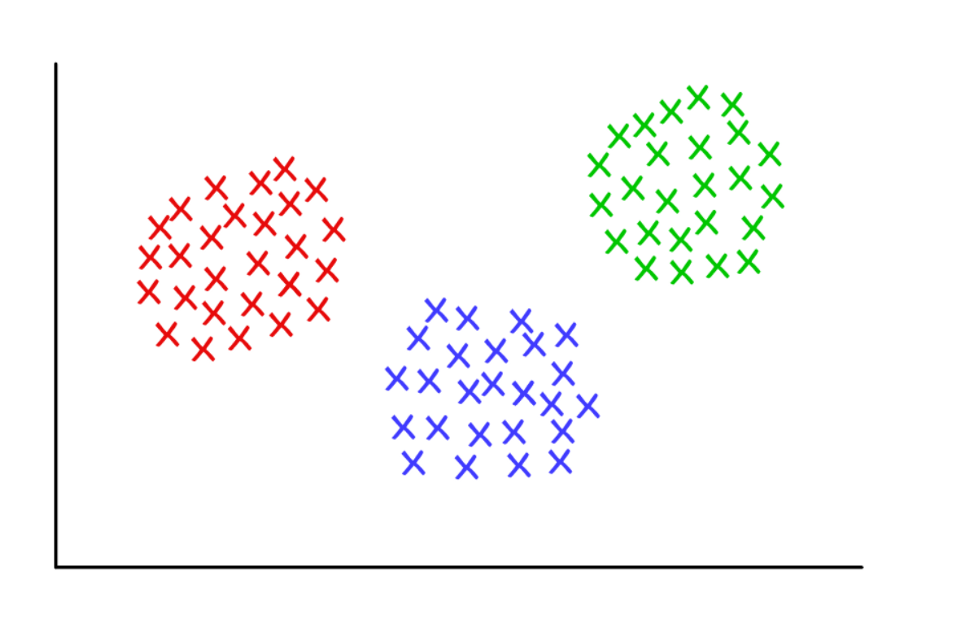Drei verdächtig saubere Cluster mit k = 3

K-bedeutet Clustering

Verwendet von:

Wenn Sie verstehen, wie viele Gruppen erhalten werden können, um eine vorgegebene (a priori) zu finden.

Wie es funktioniert:

Der Algorithmus ordnet jede Beobachtung zufällig einer von k Kategorien zu und berechnet dann den Durchschnitt für jede Kategorie. Dann ordnet er jede Beobachtung der Kategorie mit dem nächsten Durchschnitt zu und berechnet erneut die Durchschnittswerte. Der Vorgang wird wiederholt, bis Neuzuweisungen erforderlich sind.

Arbeitsbeispiel:

Nehmen Sie eine Gruppe von 12 Spielern und die Anzahl der Tore, die jeder von ihnen in der aktuellen Saison erzielt hat (zum Beispiel im Bereich von 3 bis 30). Wir teilen die Spieler beispielsweise in drei Cluster ein.

Schritt 1 : Sie müssen die Spieler zufällig in drei Gruppen aufteilen und den Durchschnitt für jede von ihnen berechnen.

Group 1 Player A (5 goals), Player B (20 goals), Player C (11 goals) Group Mean = (5 + 20 + 11) / 3 = 12 Group 2 Player D (5 goals), Player E (3 goals), Player F (19 goals) Group Mean = 9 Group 3 Player G (30 goals), Player H (3 goals), Player I (15 goals) Group Mean = 16 

Schritt 2 : Ordnen Sie jeden Spieler der Gruppe mit dem nächsten Durchschnitt zu. Zum Beispiel geht Spieler A (5 Tore) in Gruppe 2 (Durchschnitt = 9). Andererseits berechnen wir die Gruppenmittelwerte.

 Group 1 (Old Mean = 12) Player C (11 goals) New Mean = 11 Group 2 (Old Mean = 9) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) New Mean = 4 Group 3 (Old Mean = 16) Player G (30 goals), Player I (15 goals), Player B (20 goals), Player F (19 goals) New Mean = 21 

Wiederholen Sie Schritt 2 immer wieder, bis die Spieler aufhören, die Gruppe zu wechseln. In diesem künstlichen Beispiel geschieht dies bei der nächsten Iteration. Hör auf! Sie haben drei Cluster aus einem Datensatz gebildet!

 Group 1 (Old Mean = 11) Player C (11 goals), Player I (15 goals) Final Mean = 13 Group 2 (Old Mean = 4) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) Final Mean = 4 Group 3 (Old Mean = 21) Player G (30 goals), Player B (20 goals), Player F (19 goals) Final Mean = 23 

Cluster sollten der Position der Spieler auf dem Spielfeld entsprechen - Verteidiger, Innenverteidiger und Stürmer. K-means funktioniert in diesem Beispiel, da Grund zu der Annahme besteht, dass die Daten in diese drei Kategorien unterteilt werden.

Basierend auf den statistischen Leistungsschwankungen kann die Maschine somit die Position der Spieler auf dem Spielfeld für jede Mannschaftssportart rechtfertigen. Dies ist nützlich für die Sportanalyse sowie für alle anderen Aufgaben, bei denen die Aufteilung des Datensatzes in vordefinierte Gruppen dazu beiträgt, die entsprechenden Schlussfolgerungen zu ziehen.

Es gibt verschiedene Variationen des beschriebenen Algorithmus. Die anfängliche Bildung von Clustern kann auf verschiedene Arten durchgeführt werden. Wir untersuchten die zufällige Einteilung der Spieler in Gruppen, gefolgt von der Berechnung der Durchschnittswerte. Infolgedessen liegen die anfänglichen Gruppenmittelwerte nahe beieinander, was die Wiederholbarkeit erhöht.

Ein alternativer Ansatz besteht darin, Cluster zu bilden, die nur aus einem Spieler bestehen, und die Spieler dann in die nächsten Cluster zu gruppieren. Die resultierenden Cluster hängen stärker vom Anfangsstadium der Bildung ab, und die Wiederholbarkeit in Datensätzen mit hoher Variabilität nimmt ab. Bei diesem Ansatz sind möglicherweise weniger Iterationen erforderlich, um den Algorithmus zu vervollständigen, da weniger Zeit für die Aufteilung der Gruppen aufgewendet wird.

Der offensichtliche Nachteil von k-means Clustering besteht darin, dass Sie im Voraus erraten müssen , wie viele Cluster Sie haben. Es gibt Methoden zur Bewertung der Konformität eines bestimmten Satzes von Clustern. Beispielsweise ist die Quadratsumme innerhalb des Clusters ein Maß für die Variabilität innerhalb jedes Clusters. Je „besser“ die Cluster sind, desto geringer ist die gesamte Quadratsumme innerhalb des Clusters.

Hierarchisches Clustering

Verwendet von:

Wenn Sie die Beziehung zwischen den Werten (Beobachtungen) offenlegen müssen.

Wie es funktioniert:

Die Abstandsmatrix wird berechnet, in der der Wert der Zelle ( i, j ) die Metrik des Abstands zwischen den Werten von i und j ist . Dann wird ein Paar der nächsten Werte genommen und der Durchschnitt berechnet. Eine neue Distanzmatrix wird erstellt, gepaarte Werte werden zu einem Objekt zusammengefasst. Dann wird ein Paar der nächsten Werte aus dieser neuen Matrix entnommen und ein neuer Durchschnittswert berechnet. Der Zyklus wird wiederholt, bis alle Werte gruppiert sind.

Arbeitsbeispiel:

Nehmen Sie einen extrem vereinfachten Datensatz mit mehreren Arten von Walen und Delfinen. Ich bin Biologe und kann Ihnen versichern, dass viel mehr Eigenschaften für den Bau phylogenetischer Bäume verwendet werden . In unserem Beispiel beschränken wir uns jedoch auf die charakteristische Körperlänge von sechs Arten von Meeressäugern. Es wird zwei Berechnungsstufen geben.



Schritt 1 : Die Matrix der Abstände zwischen allen Ansichten wird berechnet. Wir werden die euklidische Metrik verwenden, die beschreibt, wie weit unsere Daten voneinander entfernt sind, wie die Siedlungen auf der Karte. Sie können den Unterschied in der Länge der Körper jedes Paares ermitteln, indem Sie den Wert am Schnittpunkt der entsprechenden Spalte und Zeile lesen.



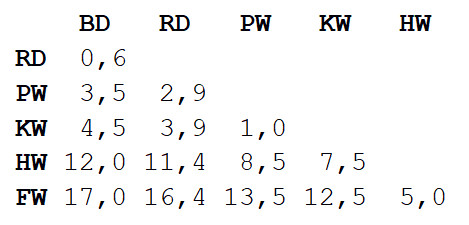Schritt 2 : Nehmen Sie ein Paar von zwei Arten, die einander am nächsten sind. In diesem Fall handelt es sich um einen Tümmler und einen grauen Delphin, bei denen die durchschnittliche Körperlänge 3,3 m beträgt.

Wir wiederholen Schritt 1 und berechnen erneut die Entfernungsmatrix. Diesmal kombinieren wir Tümmler und Grau-Delfin zu einem Objekt mit einer Körperlänge von 3,3 m.



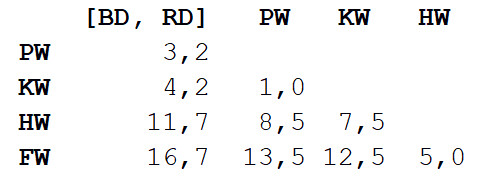
Jetzt wiederholen wir Schritt 2, jedoch mit einer neuen Distanzmatrix. Diesmal ist der Grind- und Killerwal am nächsten, also lasst sie uns zu einem Paar zusammenfassen und den Durchschnitt berechnen - 7 m.

Wiederholen Sie als Nächstes Schritt 1: Berechnen Sie erneut die Entfernungsmatrix, jedoch mit dem Mahl- und Killerwal in Form eines einzelnen Objekts mit einer Körperlänge von 7 m.



Wiederholen Sie Schritt 2 mit dieser Matrix. Der kleinste Abstand (3,7 m) liegt zwischen den beiden kombinierten Objekten, daher kombinieren wir sie zu einem noch größeren Objekt und berechnen den Durchschnittswert - 5,2 m.

Wiederholen Sie dann Schritt 1 und berechnen Sie eine neue Matrix, indem Sie Tümmler / Grau-Delfin mit Mahl- / Killerwal kombinieren.



Wiederholen Sie Schritt 2. Der kleinste Abstand (5 m) liegt zwischen dem Buckel und dem Finwale. Wir kombinieren sie also und berechnen den Durchschnitt - 17,5 m.

Wieder Schritt 1: Berechnen Sie die Matrix.



Wiederholen Sie abschließend Schritt 2 - es ist nur noch eine Entfernung (12,3 m) vorhanden, sodass wir alle zu einem Objekt vereinen und anhalten. Folgendes ist passiert:

 [[[BD, RD],[PW, KW]],[HW, FW]] 

Das Objekt hat eine hierarchische Struktur (denken Sie an JSON ), sodass es als Baumdiagramm oder Dendrogramm angezeigt werden kann. Das Ergebnis ähnelt einem Stammbaum. Je näher zwei Werte an einem Baum liegen, desto ähnlicher oder enger sind sie miteinander verbunden.


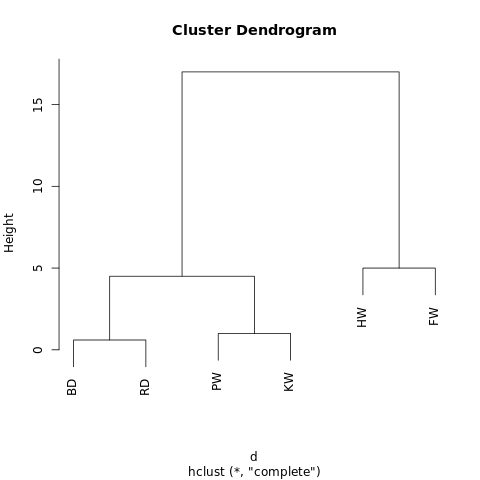Ein einfaches Dendrogramm, das mit R-Fiddle.org erstellt wurde

Die Struktur des Dendrogramms ermöglicht es Ihnen, die Struktur des Datensatzes selbst zu verstehen. In unserem Beispiel haben wir zwei Hauptzweige - einen mit Buckel und Finwal, den anderen mit einem Tümmler / Grau-Delphin und einem Mahl- / Killerwal.

In der Evolutionsbiologie werden viel größere Datensätze mit vielen Arten und einer Fülle von Zeichen verwendet, um taxonomische Beziehungen zu identifizieren. Außerhalb der Biologie wird hierarchisches Clustering in den Bereichen Data Mining und maschinelles Lernen angewendet.

Dieser Ansatz erfordert keine Vorhersage der erforderlichen Anzahl von Clustern. Sie können das resultierende Dendrogramm in Cluster aufteilen und den Baum auf die gewünschte Höhe „zuschneiden“. Sie können die Höhe je nach gewünschter Auflösung des Datenclusters auf verschiedene Arten auswählen.
Wenn beispielsweise das obige Dendrogramm in einer Höhe von 10 abgeschnitten wird, schneiden wir die beiden Hauptäste und teilen das Dendrogramm in zwei Spalten. Wenn Sie in einer Höhe von 2 schneiden, teilen Sie das Dendrogramm in drei Gruppen.

Andere hierarchische Clustering-Algorithmen können sich in drei Aspekten von den in diesem Artikel beschriebenen unterscheiden.

Das Wichtigste ist der Ansatz. Hier verwendeten wir die agglomerative Methode: Wir begannen mit einzelnen Werten und gruppierten sie zyklisch, bis wir einen großen Cluster erhielten. Ein alternativer (und rechenintensiverer) Ansatz impliziert die umgekehrte Reihenfolge: Zuerst wird ein riesiger Cluster erstellt und dann nacheinander in immer kleinere Cluster unterteilt, bis separate Werte verbleiben.

Es gibt auch verschiedene Methoden zur Berechnung von Distanzmatrizen. Euklidische Metriken sind für die meisten Aufgaben ausreichend, andere Metriken sind jedoch in einigen Situationen besser geeignet.

Schließlich kann das Verknüpfungskriterium variieren. Die Beziehung zwischen Clustern hängt von ihrer Nähe zueinander ab, aber die Definition von „Nähe“ kann unterschiedlich sein. In unserem Beispiel haben wir den Abstand zwischen den Durchschnittswerten (oder "Schwerpunkten") jeder Gruppe gemessen und die nächsten Gruppen paarweise kombiniert. Sie können jedoch eine andere Definition verwenden.

Angenommen, jeder Cluster besteht aus mehreren diskreten Werten. Der Abstand zwischen zwei Clustern kann als minimaler (oder maximaler) Abstand zwischen einem ihrer Werte definiert werden, wie unten gezeigt. Für verschiedene Kontexte ist es zweckmäßig, unterschiedliche Definitionen des Verknüpfungskriteriums zu verwenden.


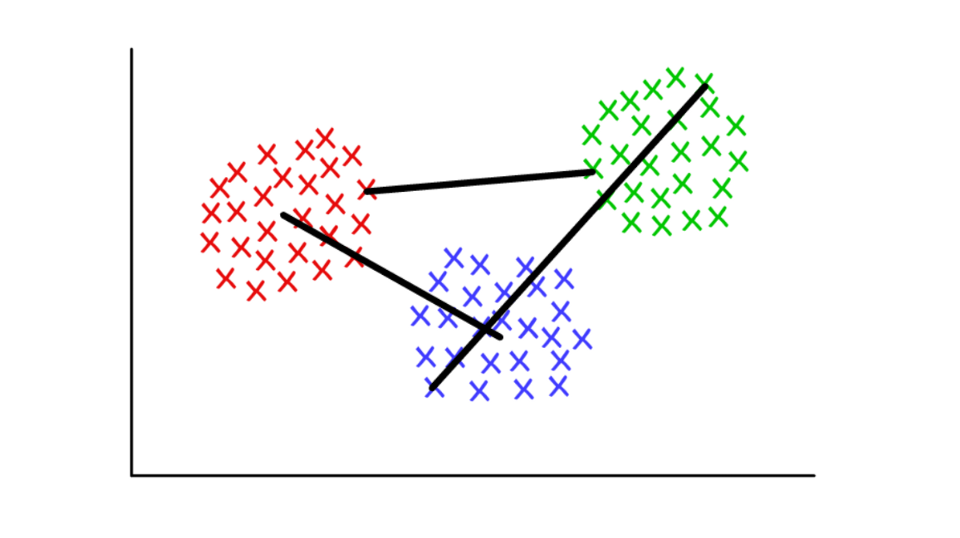Rot / Blau: Schwerpunktpool; rot / grün: Kombination basierend auf Minima; grün / blau: Zusammenführen basierend auf Höhen.

Definition von Communities in Diagrammen (Graph Community Detection)

Verwendet von:

Wenn Ihre Daten in Form eines Netzwerks oder "Diagramms" dargestellt werden können.

Wie es funktioniert:

Eine Community in einem Diagramm kann grob als Teilmenge von Scheitelpunkten definiert werden, die stärker miteinander verbunden sind als mit dem Rest des Netzwerks. Es gibt verschiedene Community-Definitionsalgorithmen, die auf spezifischeren Definitionen basieren, wie z. B. Edge Betweenness, Modularity-Maximsation, Walktrap, Clique Percolation, Leading Eigenvector ...

Arbeitsbeispiel:

Die Graphentheorie ist ein sehr interessanter Zweig der Mathematik, der es uns ermöglicht, komplexe Systeme in Form von abstrakten Mengen von „Punkten“ (Eckpunkten, Knoten) zu modellieren, die durch „Linien“ (Kanten) verbunden sind.

Vielleicht ist die erste Anwendung von Grafiken, die mir in den Sinn kommt, das Studium sozialer Netzwerke. In diesem Fall repräsentieren die Peaks Personen, die durch Rippen mit Freunden / Abonnenten verbunden sind. Sie können sich jedoch jedes System in Form eines Netzwerks vorstellen, wenn Sie die Methode der sinnvollen Verbindung von Komponenten rechtfertigen können. Innovative Anwendungen des Clustering mithilfe der Graphentheorie umfassen das Extrahieren von Eigenschaften aus visuellen Daten und das Analysieren genetischer regulatorischer Netzwerke.

Schauen wir uns als einfaches Beispiel die folgende Grafik an. Dies zeigt die acht Websites, die ich am häufigsten besuche. Die Links zwischen ihnen basieren auf Links in Wikipedia-Artikeln. Solche Daten können manuell erfasst werden, aber bei großen Projekten ist das Schreiben eines Python-Skripts viel schneller. Zum Beispiel: https://raw.githubusercontent.com/pg0408/Medium-articles/master/graph_maker.py .


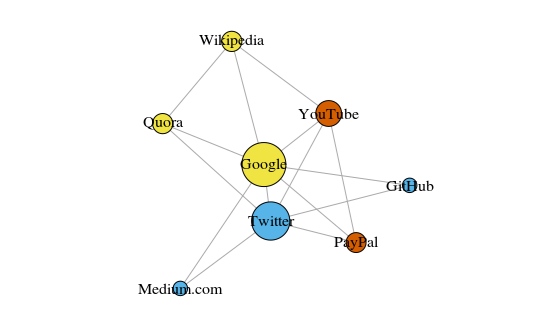Das Diagramm wird mit dem igraph-Paket für R 3.3.3 erstellt

Die Farbe der Peaks hängt von der Teilnahme an Gemeinschaften ab, und die Größe hängt von der Zentralität ab. Bitte beachten Sie, dass die zentralsten Google und Twitter sind.

Außerdem spiegeln die resultierenden Cluster reale Aufgaben sehr genau wider (dies ist immer ein wichtiger Leistungsindikator). Die Eckpunkte, die die Link- / Suchseiten darstellen, sind gelb hervorgehoben. blau hervorgehobene Websites für Online-Veröffentlichungen (Artikel, Tweets oder Code); Rot hervorgehoben sind PayPal und YouTube, die von ehemaligen PayPal-Mitarbeitern gegründet wurden. Guter Abzug für den Computer!

Neben der Visualisierung großer Systeme liegt die wahre Kraft von Netzwerken in der mathematischen Analyse. Beginnen wir mit der Konvertierung des Netzwerkbildes in ein mathematisches Format. Das Folgende ist die Adjazenzmatrix des Netzwerks.



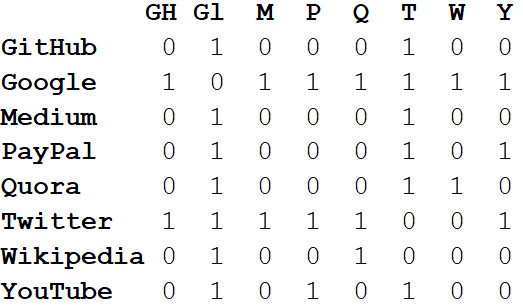
Die Werte an den Schnittpunkten von Spalten und Zeilen geben an, ob sich zwischen diesem Eckpunktpaar eine Kante befindet. Beispielsweise befindet sich zwischen Medium und Twitter am Schnittpunkt dieser Zeile und Spalte 1. Und zwischen Medium und PayPal gibt es keine Kante, sodass in der entsprechenden Zelle 0 vorhanden ist.

Wenn wir alle Eigenschaften des Netzwerks in Form einer Adjazenzmatrix darstellen, können wir alle möglichen nützlichen Schlussfolgerungen ziehen. Beispielsweise kennzeichnet die Summe der Werte in einer Spalte oder Zeile den Grad jedes Scheitelpunkts, dh die Anzahl der mit diesem Scheitelpunkt verbundenen Objekte. Normalerweise angezeigt durch den Buchstaben k .

Wenn wir die Grade aller Eckpunkte summieren und durch zwei teilen, erhalten wir L - die Anzahl der Kanten im Netzwerk. Die Anzahl der Zeilen und Spalten entspricht N - der Anzahl der Scheitelpunkte im Netzwerk.

Wenn wir nur k, L, N und die Werte in allen Zellen der Adjazenzmatrix A kennen, können wir die Modularität jeder Clusterbildung berechnen.

Angenommen, wir haben ein Netzwerk in mehreren Communities zusammengefasst. Anschließend können Sie den Modularitätswert verwenden, um die „Qualität“ des Clusters vorherzusagen. Eine höhere Modularität zeigt an, dass wir das Netzwerk in „exakte“ Communities unterteilt haben, und eine niedrigere Modularität deutet darauf hin, dass Cluster eher zufällig als vernünftig gebildet werden. Um es klarer zu machen:


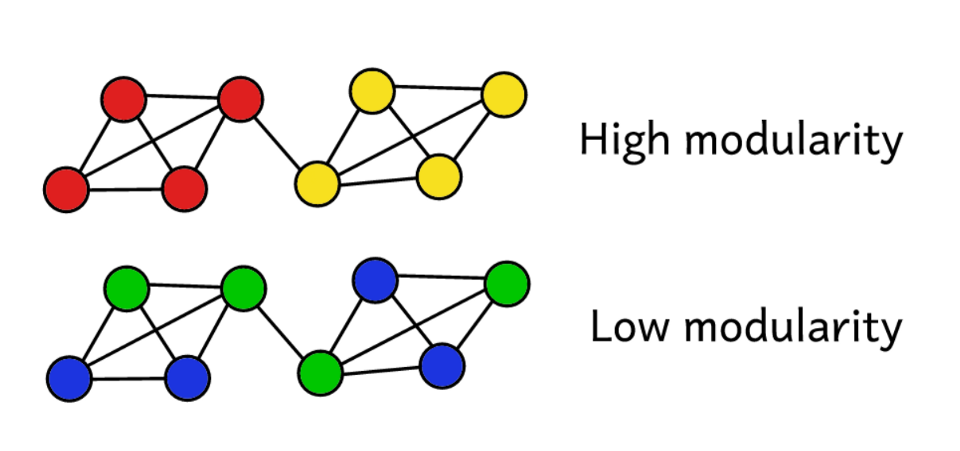
Die Modularität dient als Maß für die „Qualität“ von Gruppen.

Die Modularität kann mit der folgenden Formel berechnet werden:



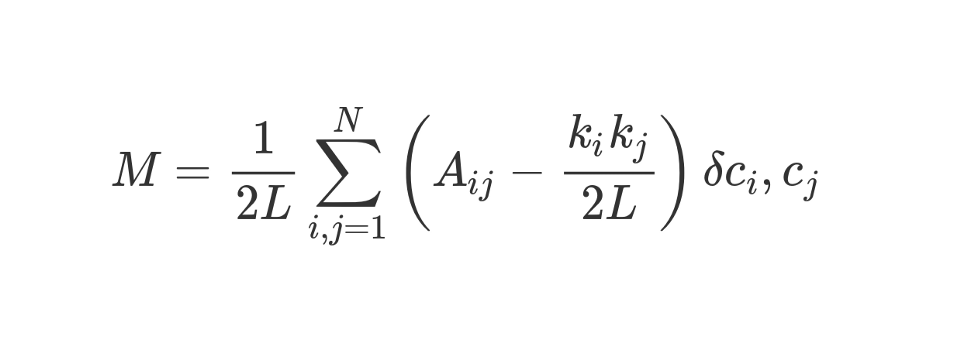
Schauen wir uns diese ziemlich fantastisch aussehende Formel an.

M , wie Sie wissen, ist dies Modularität.

Der 1 / 2L- Koeffizient bedeutet, dass wir den Rest des "Körpers" der Formel durch 2L teilen, dh durch die doppelte Anzahl von Kanten im Netzwerk. In Python könnte man schreiben:

 sum = 0 for i in range(1,N): for j in range(1,N): ans = #stuff with i and j as indices sum += ans 

Was ist #stuff with i and j ? Das Bit in Klammern sagt uns, dass wir (k_i k_j) / 2L von A_ij subtrahieren sollen, wobei A_ij der Wert in der Matrix am Schnittpunkt von Zeile i und Spalte j ist.

Die Werte k_i und k_j sind die Grade jedes Scheitelpunkts. Sie können durch Summieren der Werte in Zeile i bzw. Spalte j ermittelt werden. Wenn wir sie multiplizieren und durch 2L dividieren, erhalten wir die erwartete Anzahl von Kanten zwischen den Eckpunkten i und j, wenn das Netzwerk zufällig gemischt wurde.

Der Inhalt der Klammern spiegelt den Unterschied zwischen der tatsächlichen Struktur des Netzwerks und der erwarteten wider, wenn das Netzwerk zufällig neu aufgebaut wurde. Wenn Sie mit den Werten herumspielen, liegt die höchste Modularität bei A_ij = 1 und niedrig (k_i k_j) / 2L. Das heißt, die Modularität nimmt zu, wenn zwischen den Eckpunkten i und j eine "unerwartete" Kante liegt.

Schließlich multiplizieren wir den Inhalt der Klammern mit dem, was in der Formel als δc_i, c_j angegeben ist. Dies ist die Kronecker-Delta-Funktion. Hier ist die Implementierung in Python:

 def Kronecker_Delta(ci, cj): if ci == cj: return 1 else: return 0 Kronecker_Delta("A","A") #returns 1 Kronecker_Delta("A","B") #returns 0 

Ja so einfach. Die Funktion akzeptiert zwei Argumente. Wenn sie identisch sind, gibt sie 1 zurück. Wenn nicht, dann 0.

Mit anderen Worten, wenn die Eckpunkte i und j in einen Cluster fallen, ist δc_i, c_j = 1. Und wenn sie sich in verschiedenen Clustern befinden, gibt die Funktion 0 zurück.

Da wir den Inhalt der Klammern mit dem Kronecker-Symbol multiplizieren, ist das Ergebnis der investierten Summe Σ am höchsten, wenn die Eckpunkte innerhalb eines Clusters durch eine große Anzahl „unerwarteter“ Kanten verbunden sind. Die Modularität ist somit ein Indikator dafür, wie gut ein Diagramm in einzelne Communities gruppiert ist.

Die Division durch 2L begrenzt die obere Modularität auf Eins. Wenn die Modularität nahe 0 oder negativ ist, bedeutet dies, dass die aktuelle Clusterbildung des Netzwerks keinen Sinn ergibt. Durch die Erhöhung der Modularität können wir einen besseren Weg finden, das Netzwerk zu gruppieren.

Bitte beachten Sie, dass wir zur Bewertung der „Qualität“ des Clustering eines Diagramms im Voraus festlegen müssen, wie es gruppiert werden soll. Leider ist es aufgrund der Komplexität der Berechnungen physikalisch einfach unmöglich, alle Methoden zum Clustering eines Graphen durch Vergleichen ihrer Modularität dumm durchzugehen, es sei denn, die Stichprobe ist sehr klein.

Die Kombinatorik legt nahe, dass es für ein Netzwerk mit 8 Eckpunkten 4.140 Clustering-Methoden gibt. Für ein Netzwerk mit 16 Eckpunkten gibt es bereits mehr als 10 Milliarden Wege, für ein Netzwerk mit 32 Eckpunkten - 128 Septillionen und für ein Netzwerk mit 80 Eckpunkten wird die Anzahl der Clustering-Methoden die Anzahl der Atome im beobachtbaren Universum überschreiten.

Daher verwenden wir anstelle der Aufzählung die heuristische Methode, mit deren Hilfe Cluster mit maximaler Modularität relativ einfach berechnet werden können. Dies ist ein Algorithmus namens Fast-Greedy Modularity-Maximization , eine Art Analogon zu dem oben beschriebenen agglomerativen hierarchischen Clustering-Algorithmus. Anstatt auf der Grundlage der Nähe zu kombinieren, vereint Mod-Max Communitys in Abhängigkeit von Änderungen der Modularität. Wie es funktioniert:

Zunächst wird jeder Scheitelpunkt seiner eigenen Community zugewiesen und die Modularität des gesamten Netzwerks berechnet - M.

Schritt 1 : Für jedes Paar von Gemeinschaften, die durch mindestens eine Kante verbunden sind, berechnet der Algorithmus die resultierende Änderung der Modularität ΔM im Fall der Kombination dieser Paare von Gemeinschaften.

Schritt 2 : Dann wird ein Paar genommen, wenn kombiniert, ist ΔM maximal und kombiniert. Für dieses Clustering wird eine neue Modularität berechnet und gespeichert.

Die Schritte 1 und 2 werden wiederholt : Jedes Mal, wenn sich ein Paar von Gemeinschaften zusammenschließt, ergibt sich das größte ΔM, ein neues Clustering-Schema und sein M.

Iterationen werden beendet , wenn alle Scheitelpunkte zu einem großen Cluster zusammengefasst sind. Jetzt überprüft der Algorithmus die gespeicherten Datensätze und findet das Clustering-Schema mit der höchsten Modularität. Sie ist es, die als Gemeinschaftsstruktur zurückkehrt.

Zumindest für die Menschen war es rechenintensiv. Die Graphentheorie ist eine reiche Quelle für schwierige Rechenprobleme und NP-harte Probleme. Mithilfe von Diagrammen können wir viele nützliche Schlussfolgerungen zu komplexen Systemen und Datensätzen ziehen. Fragen Sie Larry Page, dessen PageRank-Algorithmus, mit dem Google in weniger als einer Generation von einem Startup zu einem globalen Dominanten wurde, vollständig auf der Graphentheorie basiert.

Studien zur Graphentheorie konzentrieren sich heute auf die Identifizierung von Gemeinschaften. Es gibt viele Alternativen zum Modularitätsmaximierungsalgorithmus, der zwar nützlich, aber nicht ohne Nachteile ist.

Erstens werden bei einem agglomerativen Ansatz kleine, genau definierte Gemeinschaften häufig zu größeren zusammengefasst. Dies wird als Auflösungslimit bezeichnet. Der Algorithmus weist keine Communitys zu, die kleiner als eine bestimmte Größe sind. Ein weiterer Nachteil besteht darin, dass der Mod-Max-Algorithmus anstelle eines ausgeprägten, leicht erreichbaren globalen Peaks versucht, aus vielen engen Modularitätswerten ein breites "Plateau" zu erzeugen. Infolgedessen ist es schwierig, den Gewinner zu ermitteln.

Andere Algorithmen verwenden andere Methoden zum Definieren von Communities. Beispielsweise ist Edge-Betweenness ein Teilungsalgorithmus (Teilungsalgorithmus), bei dem zunächst alle Scheitelpunkte in einem großen Cluster zusammengefasst werden. Dann werden die am wenigsten „wichtigen“ Kanten iterativ entfernt, bis alle Scheitelpunkte isoliert sind. Das Ergebnis ist eine hierarchische Struktur, bei der die Eckpunkte umso näher beieinander liegen, je ähnlicher sie sind.

Der Algorithmus Clique Percolation berücksichtigt mögliche Schnittpunkte zwischen Communities. Es gibt eine Gruppe von Algorithmen, die auf dem zufälligen Gehen in einem Graphen basieren, und es gibt spektrale Clustering- Methoden, die sich mit der spektralen Zerlegung (Eigendekomposition) der Adjazenzmatrix und anderen daraus abgeleiteten Matrizen befassen. All diese Ideen werden verwendet, um Funktionen hervorzuheben, beispielsweise in der Bildverarbeitung.

Wir werden nicht die Arbeitsbeispiele für jeden Algorithmus im Detail analysieren. , , 20 .

Fazit

, - , , . , , 20-40 .

, — , . , , .

, , , , . , - , , ? - !