Ein Artikel über die Analyse des Spiels durch ein bekanntes Handelsnetzwerk weckte
großes Interesse an
Cloud4Y . Hier sind einige Passagen, um Sie auf den neuesten Stand zu bringen:
Einmal, an einem sonnigen Frühlingsmorgen, als ich ein Stadtforum las, stieß ich auf einen Link mit einem einfachen Spiel aus einem bekannten Handelsnetzwerk. Das der Weltmeisterschaft gewidmete Spiel (Action) war ein unkompliziertes Drei-mal-Drei-Feld voller Fußbälle. Durch Klicken auf den Ball haben wir ein Bild mit einem bestimmten Produkt geöffnet. Beim Öffnen von drei identischen Bildern wurde dem Teilnehmer ein kostenloser Empfang dieses Produkts in einem der Geschäfte des Netzwerks garantiert. Außerdem befand sich unter einem der Bälle das Bild einer roten Karte, deren Eröffnung das Ende des Spiels bedeutete.
Der Autor des Artikels begann die Gründe für seinen Verlust zu untersuchen und fand auf der Grundlage der Ergebnisse der Berechnungen Folgendes heraus:
Eine kurze Skizze der Formeln auf einer Serviette, und es stellte sich heraus, dass die Gewinnwahrscheinlichkeit 1/4 beträgt. Für 5 Felder musste ich basteln, aber die berechnete Wahrscheinlichkeit betrug auch 25%.
...
Beim Ausführen des Skripts habe ich ein unerwartetes Ergebnis erzielt - 25% der Gewinne. Nachdem ich mit der Anzahl der Gewinnelemente und der Gesamtzahl der Felder gespielt hatte, stellte ich fest, dass die Gewinnwahrscheinlichkeit in einem solchen Spiel nicht von der Anzahl der Felder abhängt und gleich eins geteilt durch die Anzahl der um eins erhöhten Gewinnelemente ist.
Wir waren an der Richtigkeit einer solchen Berechnung interessiert und machten uns auf die Suche nach der mathematischen Wahrheit, indem wir die Serviette durch Excel ersetzten. Leser, die die Wahrscheinlichkeitstheorie lieben, werden zu cat eingeladen, um die Richtigkeit unserer Berechnungen zu überprüfen.
Zunächst erfahren wir die Spielregeln. Dabei half der Benutzer von Habr
Stecenko , ohne es zu wissen, in seinem
Kommentar . Er schreibt auch:
Wenn Sie sich das Skript des Autors ansehen, wird davon ausgegangen, dass drei Karten eines Produkts auf dem Spielfeld, eine Karte mit fünf anderen Waren und eine rote Karte vorhanden sein MÜSSEN, während die Beschreibung des Spiels dieser absolut nicht folgt - die Regeln sagen nichts aus dass die Gewinnkombination auf dem Spielfeld vorhanden sein muss.
Die Regeln besagen jedoch, dass insgesamt 26 Produkte beteiligt sind. Es stellt sich heraus, dass die Ausgabe von 9 Karten generiert wird: 8 Karten sind Kombinationen von 26 Produkten mit Wiederholungen, und eine Karte ist rot.
Unter solchen Bedingungen ist die Berechnung der mathematischen Gewinnwahrscheinlichkeit etwas komplizierter als der Autor des ursprünglich vorgeschlagenen Beitrags. Das Spiel besteht aus mehreren Ebenen:- Die Wahrscheinlichkeit, N Karten zu öffnen, ohne die rote zu öffnen, ist die Wahrscheinlichkeit einer anderen Spieldauer, unabhängig davon, ob es einen Preis gibt.
- Die Wahrscheinlichkeit, eine Kombination von 3 Karten mit derselben Ware zu sammeln. Diese Wahrscheinlichkeit variiert je nach Spieldauer. Es ist wichtig zu verstehen, dass ein Satz von 8 Karten mit Waren und immer einer roten Karte nicht unbedingt mindestens ein Paar identischer Karten enthält, ganz zu schweigen von drei gleichzeitig.
Beginnen wir mit einem einfachen - zu verstehen, wie sich die Anzahl der Teilnehmer mit zunehmender Anzahl der Karten, die sie aufgrund der Regel der roten Karte öffnen, verringert.
Chancen auf unterschiedliche Spiellängen
Wir berechnen, wie wahrscheinlich es ist, dass für N Versuche (offene Karten) Rot geöffnet wird.UPD: Zunächst haben wir die Wahrscheinlichkeit des Öffnens von Rot mithilfe einer Binomialverteilung berechnet. Dies garantierte uns nicht streng 1 rote Karte, bei einer solchen Verteilung gab es höchstwahrscheinlich eine rote Karte, aber es konnte entweder 0 oder alle 9 mit einer sehr, sehr geringen Wahrscheinlichkeit geben. Nochmals vielen Dank an Stecenko , der auf einen Fehler im Kommentar hingewiesen und die richtige Lösung vorgeschlagen hat .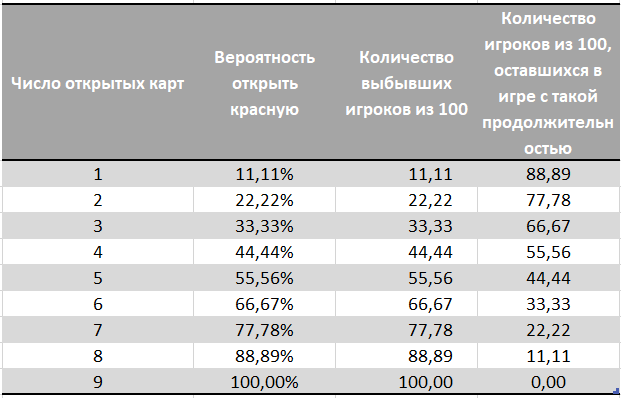
Die letzte Spalte zeigt, wie viele von hundert Spielern mit dieser Dauer im Spiel bleiben. Der Rest der Spieler scheidet aufgrund der roten Karte aus, ohne zu wissen, ob der ausgegebene Kartensatz eine Gewinnkombination enthält.
Jetzt berechnen wir die Wahrscheinlichkeiten für das Sammeln einer Kombination aus drei Karten mit derselben Ware. Dies ist eine Voraussetzung für den Erhalt eines Preises.
Preischancen
Wir zerlegen das Spiel logisch. Wir öffnen die erste Karte und wählen dann das Paar für diese Karte aus, wählen die drei für das Paar aus. Mit diesem Ansatz können wir die Wahrscheinlichkeit berechnen, in drei oder mehr Versuchen drei identische Karten zu erhalten, basierend auf der Tatsache, dass es 26 Produkte im Spiel gibt.
Für Aufgaben mit einer festen Anzahl von Tests oder Tests verwenden wir die Bernoulli-Formel - in Excel die BINOM.DIS-Funktion, wenn das Ergebnis eines Tests nur Erfolg oder Misserfolg sein kann, die Tests unabhängig sind und die Erfolgswahrscheinlichkeit während des gesamten Experiments konstant bleibt.
Mit der Funktion BINOM.RASP können Sie beispielsweise die Wahrscheinlichkeit berechnen, dass zwei der nächsten drei Neugeborenen Jungen sind. Wie hoch ist die Wahrscheinlichkeit, in drei Versuchen drei davon zu entdecken?
= BINOM.RASP (3; 3; 1/26; 0) nach Maske
= BINOM.DISP (Anzahl der Erfolge; Anzahl der Versuche; Erfolgswahrscheinlichkeit; Integral)
Oder hier ist die Formel zur Berechnung der Wahrscheinlichkeit, in 8 Versuchen 3
identische und bestimmte Waren zu erhalten.
= BINOM.RASP (3; 8; 1/26; 0), richtig?
Nicht wirklich. Wenn wir die Spieldauer in 4 Versuchen erreicht haben, das Öffnen von Rot nicht zulassen und weiter spielen, erhalten wir eine Situation mit der Möglichkeit, dass zwei Paare drei Gewinner auswählen.
Herkömmlicherweise sind zwei von 26 Waren A und B. Unsere offenen Karten sind A-B-A-B. Die Wahrscheinlichkeit ist nicht länger 1/26, sondern 1/26
+ (1/26) * "Die Wahrscheinlichkeit von zwei Paaren für eine bestimmte Spieldauer .
"Die Wahrscheinlichkeit von zwei Paaren für eine bestimmte Spieldauer = BINOM.DISP (2; 5; 1/26; 0) ^ 2
Wenn wir beim 7. Versuch ein längeres Spiel erreichen, erhalten wir Kombinationen wie A-B-A-B-B-B. Dies bedeutet, dass die Wahrscheinlichkeit jetzt gleich ist
= 1/26 * (1 + BINOM.RASP (2; 7; 1/26; 0) ^ 2 + BINOM.RASP (2; 7; 1/26; 0) ^ 3) und wir suchen eine dritte Karte für 1, 2 oder drei Paare.
UPD: Außerdem haben wir anfangs nicht berücksichtigt, dass der erste Versuch bei der Berechnung der Gewinne, der von der Wahrscheinlichkeit der Wahl des roten Gewinns befreit ist, die Entdeckung eines von 26 Produkten ist, was 100% Erfolg bedeutet. Die Anzahl der Wiederholungen eines Produkts in der Matrix ist die Anzahl der Übereinstimmungen mit einem Produkt. Dies bedeutet, dass zwei Wiederholungen für ein einzelnes Produkt ausreichen, um zu gewinnen, und nicht 3 mit einem bestimmten vorhergesagten Ergebnis. Die erste Wahl einer Karte und zwei Versuche, zwei weitere derselben Karte aufzunehmen, ergeben also insgesamt drei Experimente.Da wir die Wahrscheinlichkeiten kennen, bauen wir eine Matrix auf:
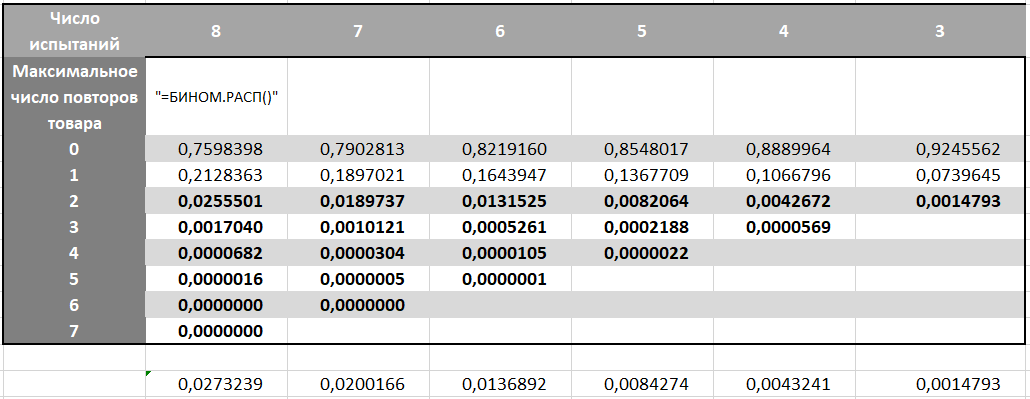
Darin finden wir die Wahrscheinlichkeit jeder maximalen Anzahl von Wiederholungen eines Produkts für jede Variante der Spieldauer. Denken Sie daran, dass sich die Gewinnwahrscheinlichkeit beim 4. Versuch und beim 7. Versuch ändert, was bedeutet, dass wir dies in der Formel BINOM.RASP berücksichtigen
Wir benötigen Optionen mit einer maximalen Anzahl von Wiederholungen eines Produkts von 3 oder mehr. Da das Spiel beendet wird, sobald wir die drei gesammelt haben, fügen wir die Wahrscheinlichkeiten durch Spalten in dem fett gedruckten Bereich hinzu.
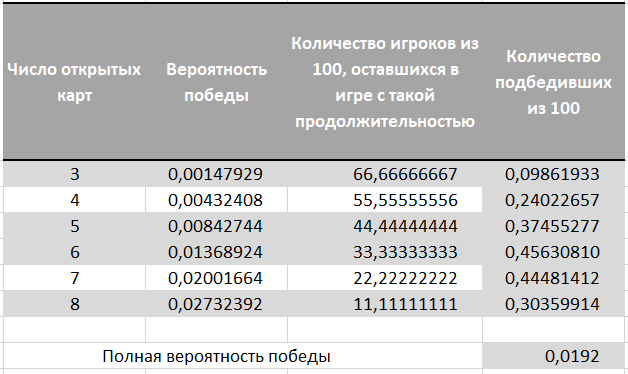
Als nächstes multiplizieren wir die Chancen jeder Spieldauer mit den Gewinnchancen eines Preises mit einer solchen Dauer. Wenn wir diese Teile zusammenfassen, erhalten wir eine Wahrscheinlichkeit von 0,0192 oder 192 Gewinnern pro 10.000 Spieler.
Ja, in der Tat ist es eine sehr geringe Wahrscheinlichkeit. Überhaupt nicht 25%. Schauen wir uns noch einmal die Spielregeln an:
8. Preisfonds:
8.1. Verfügbare Preise: Namen und Mengen
...
Insgesamt 166.000
Wir teilen 116.000 durch die Gewinnwahrscheinlichkeit und erhalten ungefähr 6 Millionen Teilnehmer, um alle Preise zu spielen. Wir erinnern daran, dass laut Rosstat am 1. Januar 2018 146 938 921 ständige Einwohner in Russland lebten. Anscheinend ist dies die Idee der Organisatoren des Spiels - eine Chance zu geben, fast jeden Bürger Russlands zu gewinnen.UPD: Die endgültige Wahrscheinlichkeit hat sich nach den Änderungen geändert. Jetzt können wir unsere Berechnungen in der Praxis mit Hilfe von Skripten testen, aber Gottes geistige Begabung der Mathematiker und Theoretiker früherer Generationen ist erstaunlich, die eine solche Anzahl von Wahrscheinlichkeiten berechnet, die richtige Lösung auf Papier gefunden und mentale Experimente durchgeführt haben.Die Analyse des Codes zeigte dem Autor der Originalveröffentlichung, dass das Skript bereits vor Spielbeginn das Ergebnis „kennt“, aber niemand weiß, welches vorgegebene Ergebnis das Skript einem bestimmten Benutzer geben wird. Wenn Sie die mathematische Seite des Problems kennen, können Sie Ihre eigenen Schlussfolgerungen über die Ehrlichkeit der Organisatoren ziehen.