Fuzzy-Logik zur Steuerung
Der Text basiert auf Materialien aus dem Buch von V. Gostev. "Fuzzy-Regler in automatischen Modellierungssystemen." Wie alle ernsthaften Veröffentlichungen zu diesem Thema ist dieses Buch mit mathematischen Berechnungen überladen und für den unvorbereiteten Leser schwierig. In der Zwischenzeit sind die Prinzipien der Erstellung und Verwendung von Fuzzy-Logik an sich recht einfach und klar. Dieser Text ist ein Versuch, ein Beispiel aus einem Buch von einer mathematischen Sprache in eine technische Sprache zu übersetzen.
Eine mögliche Abfolge des Entwurfs einer Steuerung basierend auf Fuzzy-Logik wird gezeigt, indem logische Regeln nacheinander kompliziert und Parameter unter Verwendung von Optimierungsmethoden ausgewählt werden.
Erklärung des Problems
Betrachten Sie die Synthese eines digitalen PID-Reglers und eines Fuzzy-Reglers für ein Raketensteuerungssystem nach Anstellwinkel. Mithilfe der mathematischen Modellierung bestimmen wir die Prozesse im System und geben eine vergleichende Bewertung der Qualität des Systems mithilfe synthetisierter Steuerungen.
Nehmen Sie den Anstellwinkel als Ausgangskoordinate der Rakete:  und für die Eingangskoordinate den Lenkwinkel
und für die Eingangskoordinate den Lenkwinkel  Definieren Sie die Übertragungsfunktion der Rakete in folgender Form:
Definieren Sie die Übertragungsfunktion der Rakete in folgender Form:
 wo:
wo:
 - Raketenumwandlungskoeffizient,
- Raketenumwandlungskoeffizient,
 - Dämpfungskoeffizient,
- Dämpfungskoeffizient,
 - Zeitkonstante.
- Zeitkonstante.
Im Folgenden wird die "Übertragungsfunktion" nicht in einer strengen klassischen Definition als Verhältnis von Laplace-Transformationen verwendet.
Nehmen wir bei der Untersuchung des Steuerungssystems an, dass die Abhängigkeit der Parameter der Rakete von der Flugzeit wie folgt bestimmt wird:

Um die Berechnungen zu vereinfachen, beschreiben wir den Lenkmechanismus durch die Übertragungsfunktion der integrierenden Verbindung  In diesem Fall die Systemeingabe
In diesem Fall die Systemeingabe  - gegebener Anstellwinkel, Systemleistung
- gegebener Anstellwinkel, Systemleistung  Wird der Anstellwinkel von der Rakete berechnet, ist m (t) das Steuersignal am Ausgang der Steuerung, und das Steuerobjekt wird durch die allgemeine Übertragungsfunktion beschrieben:
Wird der Anstellwinkel von der Rakete berechnet, ist m (t) das Steuersignal am Ausgang der Steuerung, und das Steuerobjekt wird durch die allgemeine Übertragungsfunktion beschrieben:

(Das analoge Lenkgetriebe und die Rakete sind im Steuerobjekt enthalten).
Das Variationsgesetz der Eingabeaktion ist durch das Polynom gegeben:

Es ist notwendig, einen Regler zu entwickeln, der die Entwicklung des Eingangseffekts unter Verwendung eines PID-Reglers und eines auf Fuzzy-Logik basierenden Reglers sicherstellt.
Auswahl der Koeffizienten der Regler.
Vergleichen Sie den Transienten mit dem PID-Regler und dem Regler basierend auf Fuzzy-Logik.
Dynamisches Objektmodell
Erstellen Sie ein dynamisches Modell in einer Strukturmodellierungsumgebung.
Die Modellschaltung selbst ist in Abbildung 1 dargestellt.
Die angegebene Aktion wird in Form eines konstanten Blocks festgelegt, eine Variable aus dem Skript wird als Parameter festgelegt. Die Parameter der Übergangsfunktion werden in Form von Variablen eingestellt.
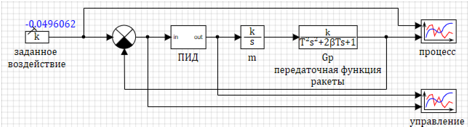 Abbildung 1. Diagramm eines dynamischen Modells einer Rakete.
Abbildung 1. Diagramm eines dynamischen Modells einer Rakete.Reglereinstellung
Der PID-Block ist ein Untermodell (Abb. 2), das den Standardblock „Diskreter PID-Regler“ verwendet. Die Abtastrate wird gleich 0,001 Sekunden gewählt.
 Abbildung 2. PID-Regler mit Abstimmkreis.
Abbildung 2. PID-Regler mit Abstimmkreis.Die Reglerparameter werden in Form von globalen Signalnamen des Projekts
Kp, Ki, Kd eingestellt. Auf diese Weise können Sie die Parameter während der Simulation ändern und den Regler einstellen.
Der Block
„Optimierung“ wurde zum Einstellen des Reglers verwendet, das Optimierungskriterium ist die minimale Standardabweichung.
Die Optimierungseinheit führt während des gesamten Übergangsprozesses eine Optimierung durch. Das Optimierungsergebnis ist ein Vektor aus drei Koeffizienten, der an den Block "In die Liste der Signale schreiben" gesendet wird, wo die berechneten Werte auf die Signale übertragen werden und sich dementsprechend die Werte der PID-Koeffizienten ändern. Um die Steuerung zu konfigurieren, stellen wir die folgenden Optimierungsparameter ein:
Anfangswerte aller Koeffizienten
1.Der Auswahlbereich liegt zwischen
-50 und
+50Auswahlgenauigkeit
0,001Maximale Standardabweichung nach Optimierung
0,01In diesem Fall berechnete die Optimierungseinheit die folgenden optimalen Werte der Koeffizienten:
Kp = -1,7498597; Ki = 17,891995; Kd = 11,606602 .
Mit diesen Koeffizienten betrug die Standardabweichung im gegebenen Übergang
0,008738090
Abbildung 3. Transient.
| 
Abbildung 4. Verwaltung. |
Fuzzy-Logik-Controller
Die Hauptvorteile einer auf Fuzzy-Logik basierenden Steuerung sind die Einfachheit und Klarheit der Bildung der Regeln zur Steuerung des Objekts.
Zum Beispiel werden in dem Buch "Fuzzy-Regler in automatischen Modellierungssystemen" die Fuzzy-Regulationsregeln zur Steuerung der Rakete durch den Anstellwinkel in Form eines mathematischen Ausdrucks beschrieben:

wo

- Systemfehler, Geschwindigkeitsänderungsfehler (erste Ableitung), Beschleunigungsfehler (zweite Ableitung);
m - Steueraktion auf das Objekt;

- Sprachliche Fehlerschätzungen, Änderungsrate des Fehlers (erste Ableitung) des Fehlers und zweite Ableitung des Fehlers, die als Fuzzy-Mengen betrachtet werden, die auf einer universellen Menge definiert sind

;;

- sprachliche Schätzungen der Steueraktion auf das Objekt, ausgewählt aus den Termmengen der Variablen
mDer Leser könnte fragen: Wie ist es, deine Mutter, tut mir leid, verstehe?
Manchmal schleichen sich Zweifel in mir ein, dass die Mathematiker selbst verstehen, was sie geschrieben haben. Hinter den abstrusen mathematischen Wendungen verbirgt sich das große Geheimnis der Regeln der Fuzzy-Regulierung. Da ist sie:
viel reduzieren
Norm - nicht berühren
klein - erhöhenWenn Sie aus der Mathematiksprache des Vogels ins Russische übersetzen, dann der Ausdruck

bedeutet wörtlich folgendes:
Wenn es
mehr als normal ist und die
Abweichung zunimmt und
die Wachstumsrate zunimmt , nehmen wir
ab .
Wenn sich die
Norm nicht ändert und die
Geschwindigkeit konstant ist ,
ändern wir
uns nicht .
Wenn es
weniger als normal ist und
fällt und
die Fallrate steigt , dann
erhöhen .
Wenn Sie verstehen, was wirklich hinter dem mathematischen Nebel verborgen ist, können Sie sich der Schaffung von Regulierungsbehörden bewusster nähern und interessantere Ergebnisse erzielen.
Ein bisschen Theorie
Um das Problem der Anpassung des Anstellwinkels zu lösen, müssen wir drei Terme aus dem Wert der kontinuierlichen Abweichung erhalten - weniger, Norm, mehr. Gleiches muss für die erste Ableitung der Abweichung und die zweite Ableitung der Abweichung erfolgen. Dies ist die erste Stufe der Fuzzy-Inferenz - Phaseneinstellung.
Um die Begriffe zu erhalten, müssen wir den numerischen Wert des Parameters für jeden Begriff festlegen. Zum Beispiel: "Little" = -1; "Norm" = 0; "Viele" = 1. Für die Phaseneinstellung verwenden wir Dreiecksfunktionen. Funktionen wachsen, wenn Sie sich dem eingestellten Wert nähern, und nehmen ab, wenn Sie sich entfernen. In Abbildung 5 sind zwei Optionen für Dreiecksfunktionen dargestellt:

 Abbildung 5. Dreieckige Zugehörigkeitsfunktionen.
Abbildung 5. Dreieckige Zugehörigkeitsfunktionen.Wenn wir die Abweichung (x1) kennen, können wir die Werte der Zugehörigkeitsfunktion für die Begriffe mehr (rote Linie), Norm (grüne Linie), weniger (blaue Linie) finden. Die Werte reichen von 0 bis 1.
Bitte beachten Sie, dass in der linken Tabelle die Extremfunktionen nicht ganz „dreieckig“ sind. Wenn wir es aus der Sicht der abstrakten Mathematik betrachten, sind die Funktionen im rechten Graphen "schöner". Wenn Sie sich jedoch an das "Hauptgeheimnis der Regeln der Fuzzy-Inferenz" erinnern, ist das linke Diagramm korrekter. Tatsächlich:
Betrachten Sie die Regel
"Add - small" . Wenn wir einen Wert von -1 haben, gilt
"little" = 1 (rote Linie) für beide Diagramme. Und wenn wir einen Wert von -2 haben? Logischerweise sollten wir auch
hinzufügen . Auf dem linken Graphen bei -2 ist es:
"little = 1" , aber auf dem rechten Graphen haben wir
"little" = 0, was offensichtlich nicht wahr ist. Gleiches gilt für die Regel
"viel reduzieren".Die Phaseneinstellung durch „ehrliche“ Dreiecksfunktionen kann dazu führen, dass wir, wenn der Wert über den Definitionsbereich von Funktionen hinausgeht, für alle Begriffe 0 erhalten, was wiederum dazu führen kann, dass keine Auswirkungen auf das Objekt auftreten.
Das umgekehrte Problem ist die Dephasifizierung. Um die Auswirkung zu berechnen, müssen Sie die inverse Transformation durchführen. Wir haben die Werte der Zugehörigkeitsfunktionen, um den Bereich (
0 ... 1 ) (Dreiecksfunktionen) und den Bereich der Effekte, die wir haben können, zu verringern, nicht zu ändern, zu erhöhen, und wir müssen einen der drei Begriffe erhalten Zahl ist eine spezifische Auswirkung.
Sie können den Aufprall auf verschiedene Arten erzielen, beispielsweise im Massenschwerpunkt der Figur. Abbildung 6 zeigt den Zustand des Controllers, in dem sich die Werte der Terme um
0,3 verringern, nicht um
0,6 ändern und um
0,8 zunehmen, wobei sich die regulatorischen Auswirkungen auf
-30..30 auswirken
.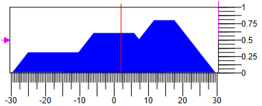 Abbildung 6. Entnazifizierung der Kontrollmaßnahme
Abbildung 6. Entnazifizierung der KontrollmaßnahmeEine weitere Option zur Entnazifizierung liegt im Massenmittelpunkt der Punkte. Abbildung 7 zeigt eine Option, bei der wir bei gleichen Werten der Begriffe und des Kontrollbereichs eine weitere Antwort erhalten.
8.82 :
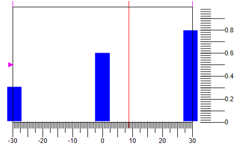 Abbildung 7. Entnazifizierung durch den Massenmittelpunkt von Punkten.
Abbildung 7. Entnazifizierung durch den Massenmittelpunkt von Punkten.Es versteht sich, dass neben der Inferenzmethode auch die Form der Zugehörigkeitsfunktion das Ergebnis beeinflusst. Sie können beispielsweise solche Dreiecksfunktionen auswählen, bei denen die Basis des Dreiecks dieselbe ist, nur die Eckpunkte unterscheiden sich. (siehe Abb. 8).
 Abbildung 8. Dreieckige Zugehörigkeitsfunktionen mit einer Basis.
Abbildung 8. Dreieckige Zugehörigkeitsfunktionen mit einer Basis.Um das Ergebnis der Phaseisierung mit den gleichen Werten der Terme 0,3 zu verringern, ändern Sie in diesem Fall nicht 0,6 und erhöhen Sie -0,8 mit dem Bereich der regulatorischen Auswirkungen -30, 30, was zu einer Auswirkung =
5,27 führt .
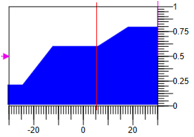 Abbildung 9. Entnazifizierung durch Flächenberechnung.
Abbildung 9. Entnazifizierung durch Flächenberechnung.Mit geheimen Kenntnissen der Fuzzy-Logik werden wir ein Controller-Modell erstellen. Wir belassen das Raketenmodell wie beim PID-Regler (siehe Abb. 1), bauen jedoch im Untermodell des Reglers die in Abb. 10 gezeigte Schaltung zusammen.
 Abbildung 10. Die Steuerschaltung basiert auf Fuzzy-Logik.
Abbildung 10. Die Steuerschaltung basiert auf Fuzzy-Logik.Am Eingang zum Regler wird eine Fehlanpassung zwischen dem angegebenen Anstellwinkel und dem realen (gemessenen) Wert angewendet. Nach dem Eingang befindet sich ein "Extrapolator" -Block, der die Umwandlung eines kontinuierlichen Signals in ein diskretes Signal mit einer bestimmten Abtastperiode ermöglicht (0,001 s entspricht dem eines diskreten PID-Reglers).
Danach werden die Abweichungen der ersten und zweiten Ableitung berechnet. Dazu berechnen wir die Differenz zwischen dem aktuellen Wert und dem Wert mit einer Verzögerung für die Quantisierungsperiode und dividieren sie durch die Verzögerungszeit (Koeffizient im Vergleichsblock). Somit erhalten wir drei Eingaben: Systemfehler, Änderungsrate (erste Ableitung) des Fehlers, Beschleunigung (zweite Ableitung) des Fehlers.
Der Wert der Eingangsvariablen wird durch Phaseisierungsblöcke in Dreiecksfunktionen umgewandelt. Für jede Variable erhalten wir drei sprachliche Variablen (insgesamt neun).
Der Demultiplexer blockiert Zuchtvektoren in sprachliche Variablen, um Regeln zu bilden. Im Diagramm sind die Namen der Variablen in der Reihenfolge ihrer Reihenfolge in den Vektoren signiert.
Die Abweichung in unserem Fall ist die Differenz zwischen der Menge und der gemessenen. Wenn ein negativer Wert bedeutet, dass der Anstellwinkel größer als die Menge ist, müssen wir ihn reduzieren. Und dementsprechend, im Gegenteil, wenn die Abweichung positiv ist, dann ist der gemessene Winkel kleiner als der angegebene, wir müssen ihn erhöhen.
(Mehr - reduzieren, weniger - erhöhen, die Norm - nicht berühren) .
Die Ausgabe enthält außerdem drei Sprachvariablen: "Reduzieren", "Nicht ändern", "Erhöhen". Der Multiplexer sammelt die Werte in einem Vektor und sendet sie an den Fuzzy-Ausgangsblock. Nachdem wir alle Variablen haben, können wir die Fuzzy-Inferenzregeln in Form eines Diagramms schreiben.
- Wenn mehr als normal und die Abweichung zunimmt und die Wachstumsrate zunimmt => abnimmt.
- Wenn sich die Norm nicht ändert und konstant ist => ändern wir uns nicht.
- Wenn es weniger als normal ist und fällt und die Fallrate steigt => steigt.
Alle sprachlichen Variablen in den Regeln sind über die logischen Blöcke „und“ verbunden und mit den Ausgängen verbunden. Wie aus 10 ersichtlich ist, unterscheidet sich die logische Fuzzy-Inferenzschaltung praktisch nicht von der üblichen logischen Schaltung, es werden nur Fuzzy-Logikblöcke verwendet.
Ähnlich wie beim Einstellen des PID-Reglers verwenden wir den Optimierungsblock.
Die Frage bleibt bei den Parametern der Blöcke.
Synthese eines Controllers basierend auf Fuzzy-Logik
Nichts ist im Leben für nichts gegeben, und daher wird die Einfachheit der Regulierungsregeln durch die Anzahl der Parameter kompensiert, die Zugehörigkeitsfunktionen beschreiben. Wenn Sie drei Koeffizienten für den PID-Regler auswählen müssen, benötigt im Fall der Fuzzy-Logik nur eine Dreiecksfunktion 3 Zahlen für die Eckpunkte. Wenn wir für jede Eingangsvariable 3 Zugehörigkeitsfunktionen + 3 für die Ausgabe benötigen, müssen wir 3 x 3 x 3 + 3 x 3 = 36 Parameter einstellen!
Aber nicht alles ist so traurig. Für eine erste Annäherung und anfängliche Einrichtung kann alles vereinfacht werden.
Nachdem Sie einige Annahmen für die anfängliche Einstellung des Controllers getroffen haben:
- Wir setzen die Symmetrie der Funktionen in Bezug auf Null, dann können Sie anstelle von zwei Zahlen für das Maximum und das Minimum eins - Max angeben und werden dementsprechend als Bereich [ -Max ... Max ] definiert.
- Wir legen eine gleichmäßige Verteilung der Funktionen fest und können dann die Position aller Eckpunkte der Dreiecke basierend auf einem bestimmten Bereich berechnen.
- Für drei Funktionen sind die Koordinaten der Eckpunkte definiert als –Max, 0, Max.
- Wir setzen, dass die Basis des Dreiecks aller Zugehörigkeitsfunktionen gleich ist.
Daher sollten wir anstelle von 36 unabhängigen Parametern nur 4 angeben, die maximale Abweichung von 0 für drei Eingangsvariablen und einen Ausgang, nämlich:
uMax - Amplitude der
Steueraktion (-uMax ... uMax) ;
deltaMax - maximale Abweichung
(-deltaMax ... deltaMax) ;
divMax - maximale Ableitung der Abweichung
(-divMax ... divMax) ;
div2Max - maximale zweite Ableitung der Abweichung
(-div2Max ... div2Max)In den Funktionen der Phaseisierung und der Fuzzy-Inferenz verwenden wir diese Signale, um die Parameter unter Berücksichtigung der akzeptierten Annahmen zu berechnen.
In dem Buch von V.V. Gostev vorgeschlagene Controller-Einstellungen "Fuzzy-Regler in automatischen Modellierungssystemen" Für den Fall der Phaseisierung durch drei Zugehörigkeitsfunktionen werden folgende Parameter vorgeschlagen:
uMax = 30 - die Amplitude der
Steueraktion ;
deltaMax = 0,01 - maximale Abweichung;
divMax = 0,07 - maximale Ableitung der Abweichung;
div2Max = 1 ist die maximale zweite Ableitung der Abweichung.
Vorübergehender Vergleich
In der grafischen Darstellung der Transienten ist die Übereinstimmung eines bestimmten Effekts mit dem erhaltenen Ergebnis nahezu vollständig:

Abbildung 11.a Transient. PID-Regler
| 
Abbildung 11.b Transient. Fuzzy-Logik
|
Offensichtliche Unterschiede sind in den Diagrammen der erhaltenen Abweichung und Kontrollwirkung zu sehen:

Abbildung 12.a. Management. PID-Regler
| 
Abbildung 12.b. Management. Fuzzy-Logik |
Aus einem Vergleich der Figuren ist ersichtlich, dass der Fuzzy-Regler weniger Fehler und einen besseren Übergang liefert.
Vergleichen wir die Transienten im System, wenn wir eine schrittweise Steueraktion festlegen. Die Ergebnisse in Abbildung 13:

Abbildung 13.a. Stufeneffekt. PID-Regler.
| 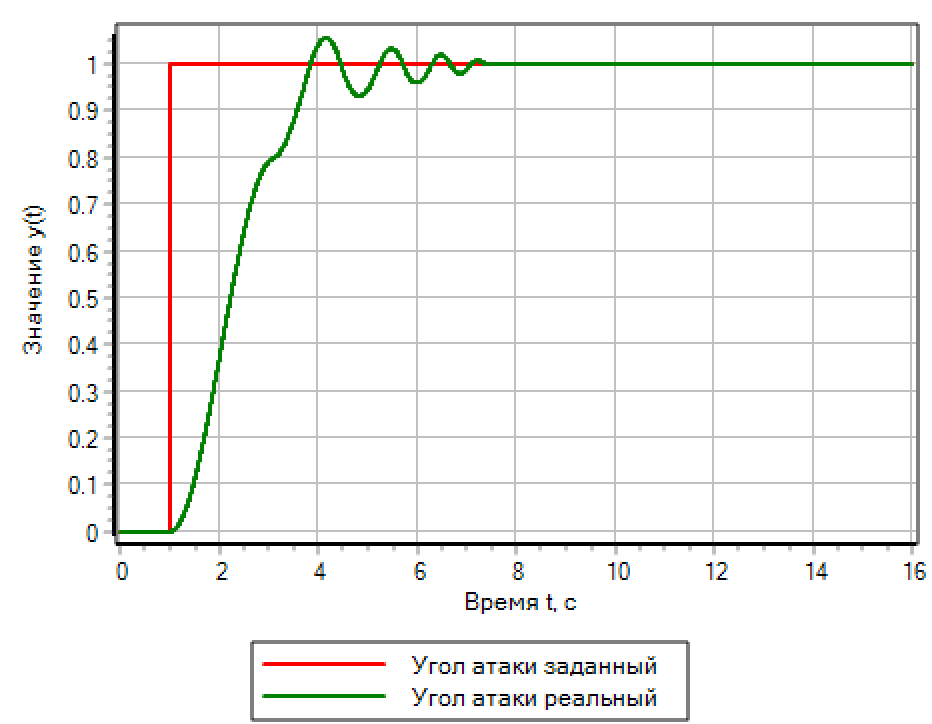
Abbildung 13.b. Stufeneffekt. Fuzzy-Logik. |
Für eine schrittweise Aktion bietet eine auf Fuzzy-Logik basierende Steuerung die beste Übergangsqualität. Der PID-Regler, der automatisch auf einen reibungslosen Ablauf eingestellt wird, verursacht Schwingungen mit Überschwingen, die doppelt so hoch sind wie der eingestellte Schritt.
Einstellung der Steuerung basierend auf Fuzzy-Logik durch Optimierungsmethode
Versuchen wir, die Parameter des Fuzzy-Reglers nach der Optimierungsmethode auszuwählen, so wie wir sie für den PID-Regler ausgewählt haben. Als Kriterium setzen wir die Standardabweichung auf weniger als 0,001.
Es ist zu beachten, dass diese Methode nicht ganz korrekt ist, da für Profis klar ist, welche Winkel und welche Geschwindigkeiten das Maximum und Minimum für jedes Konzertstück sind. Dadurch können Sie die Einschränkungen für die optimierten Parameter bewusster festlegen. Wir legen die Standardparameter fest und sehen, was passiert.
Die Optimierungsmethode mit Standardeinstellungen berechnete die folgenden Werte der Bereiche der Optimierungsparameter:
uMax = 19,377 - die Amplitude der
Steueraktion ;
deltaMax = 1,095 - maximale Abweichung;
divMax = 0,01 - maximale Ableitung der Abweichung;
div2Max = 2.497 ist die maximale zweite Ableitung der Abweichung.
Bei einer einfachen Optimierung der Abweichung liefern die erhaltenen Parameter die angegebene Genauigkeit, dies führt jedoch zu hochfrequenten Schwingungen der Regelwirkung.
Die Übergangsfunktion und die Steueraktionen sind in Abbildung 14.a dargestellt
 Abbildung 14.a. Fuzzy-Logik. Abweichungseinstellung. Abbildung 14.a. Fuzzy-Logik. Abweichungseinstellung.
| 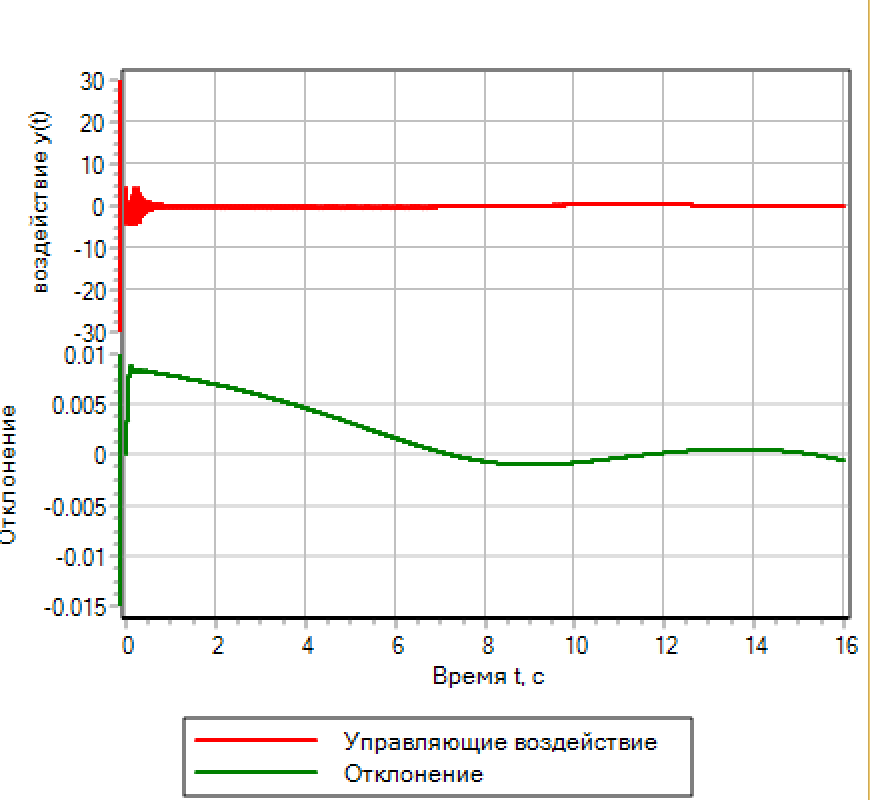 Abbildung 14.b. Fuzzy-Logik. Einstellung nach Abweichung und Anzahl der Antworten. Abbildung 14.b. Fuzzy-Logik. Einstellung nach Abweichung und Anzahl der Antworten. |
Um den Übergangsprozess zu verbessern, kann man dem Optimierungskriterium die Anzahl der Reglerwechsel vom negativen zum positiven Wert des Regulierungseffekts hinzufügen (Schema in Fig. 15).
 Abbildung 15. Schema zur Optimierung nach 2 Kriterien.
Abbildung 15. Schema zur Optimierung nach 2 Kriterien.Die Berechnung nach der Optimierungsmethode nach zwei Kriterien ergibt folgende Parameterwerte:
uMax = 19,714 - die Amplitude der
Steueraktion ;
deltaMax = 1,0496 - maximale Abweichung;
divMax = 0,01 - maximale Ableitung der Abweichung;
div2Max = 1,7931 ist die maximale zweite Ableitung der Abweichung.
Es ist ersichtlich, dass es möglich war, die Schaltfrequenz des Reglers zu reduzieren, wenn die Anzahl der Auslösungen zum Optimierungskriterium hinzugefügt wurde (siehe Abb. 14.b). Wir können also sagen, dass die Optimierungsmethode auch dann funktioniert, wenn wir nichts über die Physik des Objekts wissen und einfach die numerischen Parameter auswählen, ohne über deren physikalische Bedeutung nachzudenken.
Erstellen Sie Ihren eigenen Controller basierend auf Fuzzy-Logik
Oben haben wir den Controller nach einem bereits vorbereiteten und ziemlich einfachen Schema erstellt. Alle Begriffe der Sprachvariablen wurden durch den logischen Operator I verbunden. Da wir an den Ein- und Ausgängen die gleiche Anzahl von Begriffen haben, ist dies die einfachste und naheliegendste Lösung.
Versuchen wir, einen Controller zu erstellen, dessen Ausgabe nicht drei Terme enthält, sondern beispielsweise 5:
schnell reduzieren, reduzieren, nicht ändern, erhöhen, schnell erhöhen . Und am Eingang das gleiche.
Lassen Sie uns zunächst die Logik des Reglers ändern und den Regelalgorithmus so weit wie möglich vereinfachen.Wir schreiben die Regeln auf:1) Wenn es größer ist und wächst, t => schnell abnehmen.2) Wenn mehr => abnehmen.3) Wenn sich die Norm => nicht ändert.4) Wenn weniger => erhöhen.5) Wenn weniger und haben menshaetsya => Anstieg schnell.In diesem Fall haben wir 5 Terme (5 Dreiecksfunktionen) für die Ausgabevariable. Wir akzeptieren, dass sie gleichmäßig zwischen -uMax und + uMax verteilt sind., , , (. . 5).
.
(.. 7).
15.
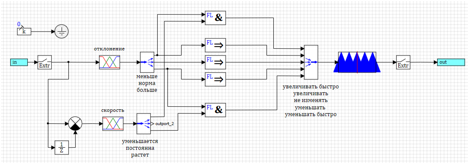 15. .
15. .«». , , .
16.
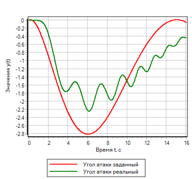 16. .
16. ., , . , , . , , , .
1)
=> .2) Wenn die Norm zunimmt und zunimmt => abnimmt.3) Wenn sich die Norm => nicht ändert.4) Wenn die Norm und abnimmt => erhöhen.5) Wenn größer und wachsend => schnell abnehmen.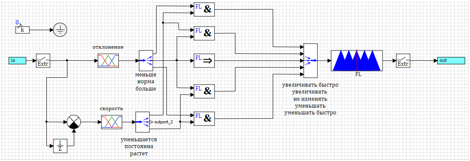 Abbildung 17. Kontrolle durch die Änderungsrate der Abweichung.Die Ergebnisse des Betriebs der Steuerung, die durch das Optimierungsverfahren eingestellt wurden, sind in den 18a und 18b dargestellt.
Abbildung 17. Kontrolle durch die Änderungsrate der Abweichung.Die Ergebnisse des Betriebs der Steuerung, die durch das Optimierungsverfahren eingestellt wurden, sind in den 18a und 18b dargestellt.
Abbildung 18.a. Der Übergangsprozess.
| 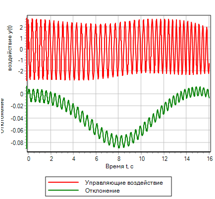
Abbildung 18.b. Management |
. , , . , . 19 , , , 1.
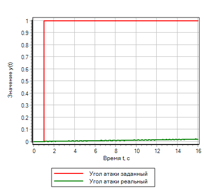
19.. .
| 
19.. . |
, , . , , . , , :
1)
=> .2) (
)
=> .3)
=> .4) (
)
=> .5)
=> .20.
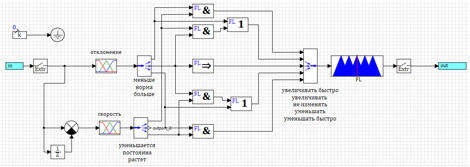 20. .
20. ., , (. . 21).
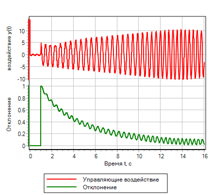
21.. .
| 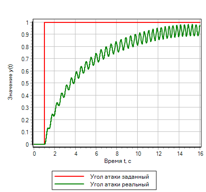
21.. . |
, «» .
, , . , , , .
, . , , . , , , :
1)
=> .2) (
normal und konstant und beschleunigt ) oder mehr => abnehmen .3) Wenn sich die Norm => nicht ändert.4) Wenn ( normal und konstant und verlangsamt ) oder weniger => erhöhen.5) Wenn größer und wachsend => schnell abnehmen .Die Schaltung dieses Reglers ist in Abbildung 22 dargestellt. Um Platz auf der Schaltung zu sparen, werden die in den Regeln in Klammern angegebenen logischen Ausdrücke „und“ im mit „ & “ gekennzeichneten Untermodell berechnet .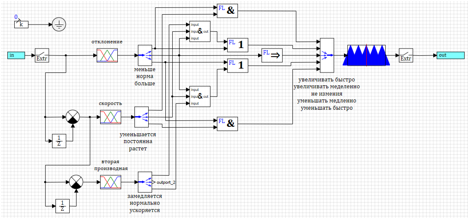 Abbildung 22. Fuzzy-Logik-Controller mit Steuerung der zweiten Ableitung.Nach Auswahl der Parameter durch die Optimierungsmethode für die Abweichung und die Anzahl der Einschlüsse wurden die folgenden Parameter erhalten:uMax = 27,4983 - die Amplitude der Steueraktion ;deltaMax = 0,0433 - maximale Abweichung;divMax = 0,0966 - maximale Ableitung der Abweichung;div2Max = 1.0828 - die maximale zweite Ableitung der Abweichung.Der Übergangsprozess ist in Abbildung 23 dargestellt. Es ist ersichtlich, dass der resultierende Regler von allen oben genannten die beste Leistung aufweist, jedoch für einen bestimmten Effekt. Abweichungen und Kontrollmaßnahmen sind das Minimum aller in diesem Text berücksichtigten.
Abbildung 22. Fuzzy-Logik-Controller mit Steuerung der zweiten Ableitung.Nach Auswahl der Parameter durch die Optimierungsmethode für die Abweichung und die Anzahl der Einschlüsse wurden die folgenden Parameter erhalten:uMax = 27,4983 - die Amplitude der Steueraktion ;deltaMax = 0,0433 - maximale Abweichung;divMax = 0,0966 - maximale Ableitung der Abweichung;div2Max = 1.0828 - die maximale zweite Ableitung der Abweichung.Der Übergangsprozess ist in Abbildung 23 dargestellt. Es ist ersichtlich, dass der resultierende Regler von allen oben genannten die beste Leistung aufweist, jedoch für einen bestimmten Effekt. Abweichungen und Kontrollmaßnahmen sind das Minimum aller in diesem Text berücksichtigten.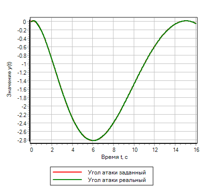
Abbildung 23.a. Der Übergangsprozess.
| 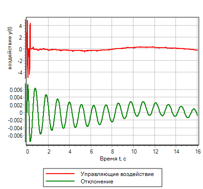
Abbildung 23.b. Management. |
Schlussfolgerungen
, -.
.
. .
, ,
...