Hierarchische Schlüsselgenerierung

In diesem Artikel werden wir über deterministische Geldbörsen, die hierarchische Schlüsselgenerierung und deren mathematische Funktionsweise sprechen. In welchen Fällen ist es praktisch, sie in die Praxis umzusetzen. Dieses Material ist für Spezialisten nützlich, deren Aktivitäten sich auf Zahlungsgateways, Bitcoin-Geldbörsen und andere Münzgeschäfte beziehen. Darüber hinaus ist das Material für diejenigen von Interesse, die sich für die Bereitstellung von elliptischen Kryptografien und Schlüsseln für die elektronische Signatur interessieren.

Deterministische Brieftasche

Definieren wir zunächst, was eine deterministische Geldbörse ist. Wenn wir über die Schlüsselgenerierung sprechen, verwenden wir häufig das Wort „Brieftasche“, da der Besitz eines privaten Schlüssels im Zusammenhang mit Kryptowährungen ein Beweis für den Besitz von Münzen ist und in diesem Fall Brieftasche und Schlüssel eine ähnliche Bedeutung haben.

Deterministic Wallet ist eine Brieftasche, in der alle verwendeten privaten Schlüssel aus einem Geheimnis generiert wurden, das von allen Schlüsseln gemeinsam genutzt wird. Die Besonderheit ist, dass es aus einem Geheimnis möglich ist, eine beliebige Anzahl von Schlüsselpaaren für die elektronische Signatur zu erzeugen. Sie können für jede eingehende Zahlung und Änderung neue Adressen verwenden.

Praktischerweise können die Schlüssel einer solchen Brieftasche einfach auf ein anderes Gerät übertragen, eine Sicherungskopie erstellt und dann wiederhergestellt werden, da Sie tatsächlich nur ein Hauptgeheimnis reservieren müssen. Außerdem sind nicht alle aus dem Hauptgeheimnis generierten privaten Schlüssel miteinander verbunden. Es ist unmöglich, die Verbindung zwischen den generierten Adressen zu verfolgen (um festzustellen, ob sie alle einem Benutzer gehören), und mit dem generierten privaten Schlüssel können Sie das gemeinsame Geheimnis nicht wiederherstellen.

Grundlegende geheime Kodierung

Lassen Sie uns nun über die Kodierung des Hauptgeheimnisses sprechen. Es gibt einen standardisierten Ansatz, der in BIP39 definiert wurde. Dies ist die sogenannte Check Encoding-Codierung des Hauptgeheimnisses in eine mnemonische Phrase - eine Reihe von Wörtern, die leicht auf Papier zu schreiben sind und bei Bedarf zu merken sind. Bei der Eingabe ist es möglich, die Prüfsumme zu überprüfen, dh gegebenenfalls einen Fehler mit einer ziemlich hohen Wahrscheinlichkeit zu identifizieren.



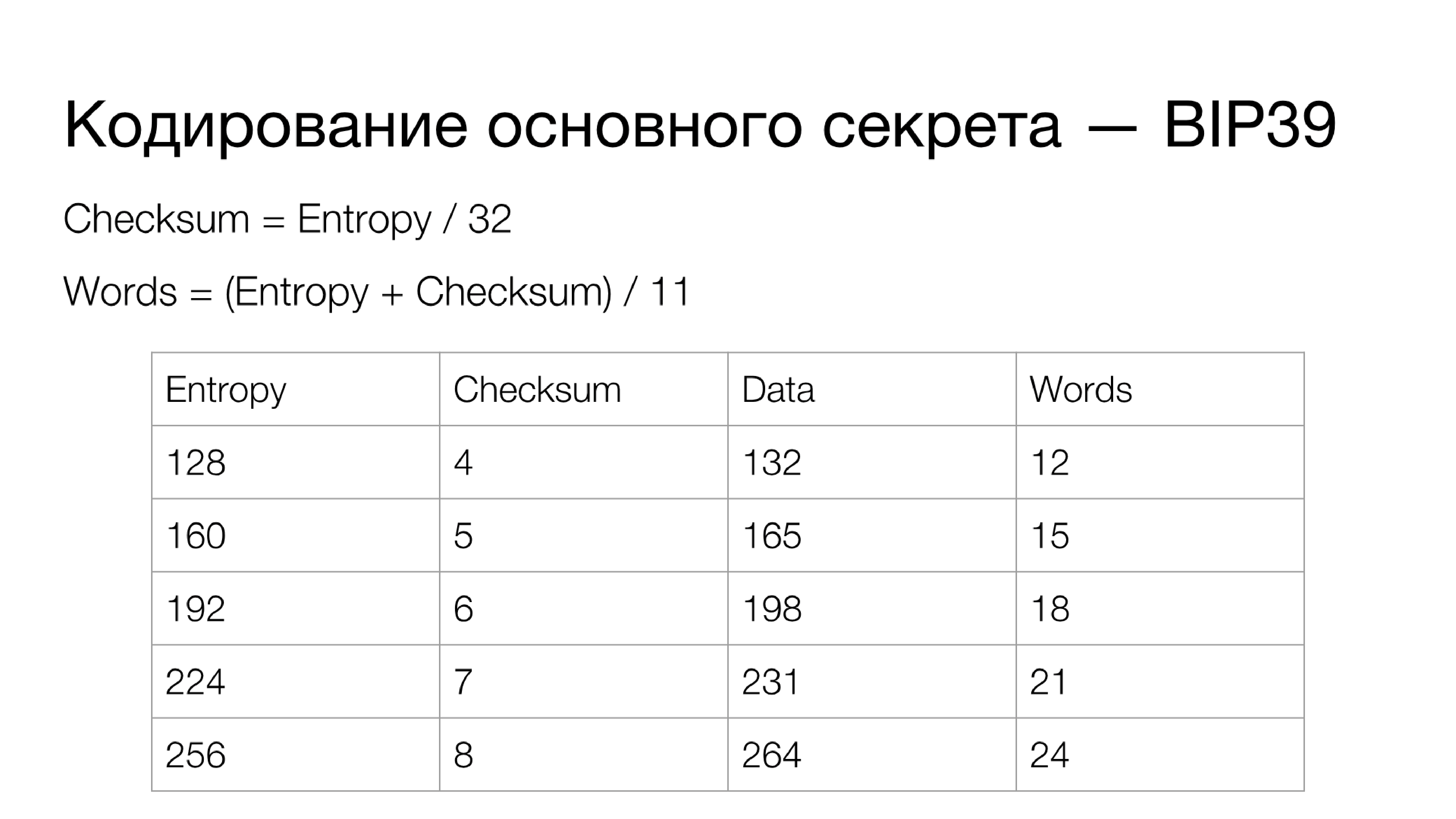
Wie funktioniert es In der Tat haben Sie das Hauptgeheimnis (Entropie) - die Daten, aus denen alle persönlichen Schlüssel der Brieftasche erweitert werden. Dieses Geheimnis kann unterschiedlich lang sein. Was die Prüfsumme betrifft: Für jeweils 32 Bits Entropie gibt es 1 Bit der Prüfsumme, dh die Prüfsumme wird nach der Formel als Länge der Entropie in Bits geteilt durch 32 berechnet.

Die Entropie verkettet sich mit einer Prüfsumme, die als doppelter SHA-256-Hash (SHA-2 mit einer Länge von 256 Bit) berechnet wird. Danach wird die erforderliche Anzahl von Bits abgeschnitten. Verkettete Daten werden auf ein anderes Zahlensystem übertragen: von binär auf das Zahlensystem auf der Basis von 2048 (wie Sie sehen können, ist 2048 $$$2 ^ {11}$) Wenn Sie die Länge der Entropiebits und die Prüfsumme addieren, erhalten Sie ein Vielfaches von 11. Somit erhalten wir die Anzahl der Wörter in der ausgegebenen Mnemonik.

Tatsächlich werden die Daten in 11-Bit-Teile "aufgeteilt". Es gibt ein Wörterbuch mit 2048 Wörtern ( $$$2 ^ {11}$) für die bestimmte Anforderungen gelten. Die Standardsprache des Wörterbuchs ist Englisch, aber jeder kann verwendet werden. Wörter sollten eine bestimmte Länge nicht überschreiten (normalerweise maximal 7 Zeichen). Alle von ihnen müssen in UTF-8 mit einer bestimmten Normalisierung aller Zeichen codiert sein. Obligatorisch ist die Eindeutigkeit jedes Wortes in den ersten vier Zeichen.

Die ersten vier Zeichen identifizieren das Wort im Wörterbuch eindeutig, und die verbleibenden Zeichen werden verwendet, um dieses Wort in einer bequemen Form zum Lesen, Speichern usw. zu vervollständigen. Somit erhält jedes aus 11 Bits bestehende Datenelement eine eindeutige Übereinstimmung in Form eines Wortes von Wörterbuch. Wenn die Entropie Ihres Geheimnisses 256 Bit beträgt, betragen die Daten für die Codierung 264 Bit, und Ihre mnemonische Phrase enthält 24 Wörter. Dies ist der Hauptansatz zum Verschlüsseln von Brieftaschengeheimnissen in BIP39, der in der Praxis am häufigsten verwendet wird.

Um in Zukunft eine Sicherungskopie zu erstellen und diese zu verwenden, können Sie diesen Satz auf ein externes Medium schreiben. Papier, das Sie an einem sicheren Ort aufbewahren, ist am besten geeignet. So können Sie den vollständigen Zugriff auf alle Ihre Schlüssel wiederherstellen.

Arten von deterministischen Geldbörsen

Es gibt zwei Arten von deterministischen Geldbörsen. Betrachten Sie ihre Hauptunterschiede.

Der erste ist der einfachste. Das Hauptgeheimnis hier ist mit dem Index des untergeordneten Schlüssels verknüpft, den wir erhalten möchten, wonach die verketteten Daten gehasht werden. Meistens geschieht dies mit der SHA-256-Hash-Funktion.

Der zweite Typ umfasst hierarchisch deterministische Wallets (HD Wallets), deren Prinzipien in BIP32 definiert sind und ein sehr verbreiteter Ansatz für die hierarchische Schlüsselgenerierung sind.

Determininistische Generation

Berücksichtigen Sie die Unterschiede zwischen diesen Brieftaschentypen im Diagramm.



Eine gewöhnliche deterministische Geldbörse hat einen Samen, aus dem eine große Anzahl privater Schlüssel direkt generiert wird. Ihre Anzahl kann nur durch die Dimension des Index begrenzt werden, der vor dem Hashing mit dem Geheimnis verknüpft wird. Normalerweise sind es 4 Bytes, das heißt, der Platz möglicher Optionen ermöglicht ungefähr 4 Milliarden eindeutige deterministische Brieftaschenschlüssel. In der Praxis sollte dies für jede Situation ausreichen.

Hierarchische deterministische Erzeugung

Kommen wir zu einer hierarchischen deterministischen Brieftasche, deren zentrales Bereitstellungsschema bisher in vereinfachter Form dargestellt wurde. Es gibt Seed, aus dem ein Paar Hauptschlüssel direkt erhalten wird. Wenn wir in einer gewöhnlichen deterministischen Brieftasche einen privaten Schlüssel erhalten, erhalten wir hier ein Schlüsselpaar. Darüber hinaus gibt es Hierarchieebenen, auf denen wir jeweils den Index berechnen, um den untergeordneten Schlüssel zu generieren. Wir können auch Zweigstellen mit öffentlichem und privatem Schlüssel bauen.

Hierarchieebenen

In Bezug auf HD-Wallets ist zu beachten, dass ein Spawning-Knoten gemäß den BIP32-Regeln auf jeder Hierarchieebene drei Objekte hat: einen privaten Schlüssel, einen öffentlichen Schlüssel und einen Kettencode, mit dem die nächste Hierarchieebene erzeugt wird.

Hierarchisches Generierungsschema

Betrachten wir das Schlüsselgenerierungsschema für BIP32 genauer.



Alles beginnt mit Seed, es wird auch Master Seed genannt, aus dem die Nullstufe der Hierarchie berechnet wird - ein Paar Hauptschlüssel und Kettencode.

Aus einem Paar von Hauptschlüsseln kann eine große Anzahl von Schlüsselpaaren mit bestimmten Indizes generiert werden. Es wird eine neue Hierarchieebene gebildet, mit der Konten generiert werden. Angenommen, ein Benutzer hat einen Startwert und möchte mehrere Adressen erstellen, die sich voneinander unterscheiden. Die Münzen dieser Adressen werden nicht gemischt, nicht zusammen veröffentlicht, und bei abgeschlossenen Transaktionen zwischen ihnen kann keine Verbindung gefunden werden. Diese Schlüssel werden vollständig getrennt voneinander verwendet. In einem der Konten wird die Schlüsselgruppe für das Arbeitsbudget verwendet, in dem anderen für das persönliche Budget und in einem anderen Konto für die schwarze Buchhaltung. Münzen vermischen sich nicht miteinander.

Die nächste Hierarchieebene definiert verschiedene Schlüsselgenerierungsketten. Am häufigsten werden Ketten mit den Indizes 0 und 1 verwendet. Eine Kette mit Index 0 generiert endgültige Schlüssel, um eine Adresse für eingehende Zahlungen zu bilden, und eine Kette mit Index 1 generiert Brieftaschen für Münzen, die der Benutzer an sich selbst sendet, d. H. Ändern. Dies ist erforderlich, damit die Brieftasche auf Programmebene von außen gesendete Zahlungen von der Änderung unterscheidet, die Änderungen im Saldo jeder Transaktion berechnet und eine visuelle Liste mit dem Verlauf aller Zahlungen erstellt. Dies vereinfacht die Entwicklung der Brieftasche und deren Verwendung für alltägliche Zahlungen.

Hash-basierter Nachrichtenauthentifizierungscode

Kommen wir nun zur mathematischen Komponente hierarchischer Schlüsselgenerierungsprozesse. Betrachten Sie zunächst den Hash-basierten Nachrichtenauthentifizierungscode. Dies ist eine andere Klasse zur Berechnung von Hash-Funktionen. Es unterscheidet sich darin, dass am Eingang zwei Werte und nicht einer verwendet werden. Der erste Wert ist der private Schlüssel und der zweite ist die Nachricht selbst.

$$

$$HMAC (K, m) = H ((K ^ {opad}) || H (K ^ {ipad}) || m))$$

K ist der Schlüssel
m - Nachricht
opad, ipad - einige konstante Werte, die zum Generieren von Schlüsseln erforderlich sind, die sich in verschiedenen Phasen des Hashings voneinander unterscheiden.
Als Hash-Funktion wird SHA-512 verwendet.

Die Besonderheit ist, dass Sie zur Verwendung von HMAC einen geheimen Schlüssel besitzen müssen, um den korrekten Hashwert der Nachricht zu erhalten.

Um den HMAC-Hashwert zu berechnen, entspricht der Wert des XOR-Schlüssels dem konstanten Wert des ipad. Danach wird das Ergebnis gehasht. Eine Nachricht wird mit diesem Wert verkettet, wonach der Schlüssel XOR mit einem konstanten Wert berechnet, mit einem Hashwert verkettet und dann erneut gehasht wird. Als Ergebnis erhalten wir 512 Bits des Hashwerts.

Ableitungsfunktionen

Schauen wir uns einige Funktionen an, die bei der Berechnung hierarchischer Schlüssel verwendet werden.



Zunächst möchten wir den Master-Seed in ein Master-Schlüsselpaar umwandeln. Danach müssen Sie den untergeordneten privaten Schlüssel und den untergeordneten öffentlichen Schlüssel vom persönlichen übergeordneten Schlüssel abrufen. Im zweiten Fall wird genau die gleiche Funktion wie im ersten Fall verwendet, aber die Multiplikation der Zahl mit dem Basispunkt wird addiert, daher wird sie nicht separat betrachtet. Der nächste Schritt besteht darin, die untergeordnete Öffentlichkeit vom öffentlichen übergeordneten Schlüssel abzurufen. Es ist anzumerken, dass es nicht möglich ist, ein persönliches Kind vom öffentlichen Schlüssel des Elternteils zu erhalten. Diese Einschränkung ist auf bestimmte Eigenschaften von HD-Geldbörsen zurückzuführen, die wir weiter betrachten werden.

Lassen Sie uns also jede der Generierungsfunktionen separat durchgehen.



Um den Hauptschlüssel von der Haupt-Sid zu erhalten, wird die HMAC-Funktion verwendet, bei der die konstante Zeichenfolge "Bitcoin Seed" als Schlüssel und die wichtigsten geheimen Daten selbst als Nachricht übertragen werden. Somit wird ein Hashwert von 512 Bits erhalten, den wir als zwei Teile betrachten: links und rechts. Die linke Seite ist der private Hauptschlüssel und die rechte Seite ist der Kettencode. Darüber hinaus werden diese Werte verwendet, um nachfolgende Ebenen von untergeordneten Schlüsseln zu generieren.

Um den Master öffentlich zu machen, multiplizieren Sie einfach den Wert des Basispunkts mit dem Wert des privaten Masterschlüssels. Wie Sie sehen können, geschieht dies in Analogie zu gewöhnlichen Tasten in einer Gruppe von Punkten auf einer elliptischen Kurve.

Nun wollen wir sehen, wie der untergeordnete private Schlüssel vom übergeordneten privaten stammt.



Wir werden die HMAC-Funktion wieder verwenden. Als Schlüssel übergeben wir den Kettencode der aktuellen Hierarchieebene und als Nachricht die Verkettung, wobei der erste Teil der persönliche übergeordnete Schlüssel multipliziert mit dem Basispunkt ist. In der Tat ist dies eine Besetzung zu einem Punkt und eine Serialisierung dieses Punktes. Die Verkettung erfolgt mit dem Index des untergeordneten Schlüssels, den wir empfangen möchten, serialisiert mit 32 Bit, dh 4 Byte.

Basierend auf dem Ergebnis der HMAC-Funktion erhalten wir den Wert I und betrachten ihn erneut getrennt: Der linke und der rechte Teil der Ausgabewerte sind 256 Bit. Dann der untergeordnete private Schlüssel $$$k_i$Wir berechnen durch Addition zum linken Ausgabewert $$$I_l$Werte des übergeordneten privaten Schlüssels. Die Addition erfolgt modulo n, wobei n die Reihenfolge des Basispunkts der elliptischen Kurve ist, um den Maximalwert des privaten Schlüssels nicht zu überschreiten. So haben wir einen untergeordneten privaten Schlüssel erhalten.

Dementsprechend ist der untergeordnete Kettencode gleich dem richtigen Ausgabewert der HMAC-Funktion, d.h. $$$I_R$. Wenn wir den untergeordneten öffentlichen Schlüssel aus dem persönlichen übergeordneten Schlüssel ermitteln möchten, multiplizieren wir den Wert $$$k_i$durch den Wert des Basispunkts auf der elliptischen Kurve. So bekommen wir den öffentlichen Schlüssel $$$K_i$.

Wie berechnen wir den öffentlichen Schlüssel des Kindes aus dem öffentlichen Elternschlüssel?



Hier wird die Berechnung etwas anders sein. Wir übergeben die Kettenhierarchie der aktuellen Hierarchieebene als Schlüssel an die HMAC-Funktion. Anschließend serialisieren wir den übergeordneten öffentlichen Schlüssel und verketten ihn mit dem gewünschten Index, der auf 32 Bit serialisiert ist. Die Eingabedaten werden genauso wie im vorherigen Fall erhalten. Um den öffentlichen Schlüssel zu berechnen, nehmen wir die linke Seite des Ausgabewerts der HMAC-Funktion und betrachten ihn als 256 Bit modulo in der Reihenfolge des Basispunkts, bringen ihn zu einem Punkt auf der elliptischen Kurve, dh multiplizieren mit dem Basispunkt, und addieren das Ergebnis mit dem übergeordneten öffentlichen Schlüssel . Das Ergebnis der Hinzufügung wird ebenfalls ein Punkt sein und es wird ein öffentlicher untergeordneter Schlüssel sein. Der Kettencode für diesen Schlüssel befindet sich auf der rechten Seite des Ausgabewerts der HMAC-Funktion.

Übereinstimmende Schlüssel zueinander

Dies kann eine logische Frage aufwerfen, wie private und öffentliche Schlüssel, die auf unterschiedliche Weise erhalten werden, einander entsprechen. Ist es wirklich möglich, aus einem öffentlichen Schlüssel, der auf öffentliche Weise generiert wurde, genau den gleichen Wert zu erhalten, indem ein auf andere Weise erhaltener privater Schlüssel mit einem Basispunkt multipliziert wird? Dies ist leicht zu überprüfen.



Wenn wir uns daran erinnern, wie wir den persönlichen untergeordneten Schlüssel berechnet haben, und ihn mit dem Basispunkt multiplizieren, dh zur Punktfunktion führen, und dann die Berechnung des untergeordneten öffentlichen Schlüssels aufrufen und diese Berechnungen vergleichen, werden wir feststellen, dass wir den übergeordneten öffentlichen Schlüssel als Produkt des persönlichen übergeordneten Schlüssels betrachten Schlüssel zum Basispunkt, dann werden wir sehen, dass die gleichen Berechnungen nur in einer anderen Reihenfolge durchgeführt wurden.

In einem Fall haben wir die privaten Schlüssel hinzugefügt und mit dem Basispunkt multipliziert, und im zweiten Fall haben wir zuerst die Werte mit dem Basispunkt multipliziert und sie dann hinzugefügt und das Ergebnis erhalten. Basierend auf der Tatsache, dass das Hinzufügen von Punkten auf einer elliptischen Kurve additiv ist, können wir sagen, dass diese beiden Werte gleich sind - wir erhalten denselben öffentlichen Schlüssel, der auf zwei Arten berechnet wird.

Beispiel für einen öffentlichen Schlüssel

Aus Gründen des Interesses können wir uns ein Beispiel eines öffentlichen Schlüssels ansehen, der für Testwerte und BIP32-Berechnungen erhalten wurde. Wenn unsere Entropie aus 128 Bit bestand, sieht sie im Hexadezimalzahlensystem wie im Bild unten aus.



Der gleiche Wert, der in der BIP39-Mnemonik codiert ist, sieht aus wie die 12 gezeigten Wörter. Wenn Sie diese Mnemonik als Master-Seed für die hierarchische Schlüsselgenerierung verwenden, erhalten Sie einen solchen privaten Master-Schlüssel mit dem entsprechenden 256-Bit-Kettencode.

Erweiterte Schlüssel

Es gibt auch Konzepte wie den erweiterten öffentlichen Schlüssel und den erweiterten privaten Schlüssel. Wie wird es verwendet? Zum besseren Verständnis beschreiben wir die visuelle Situation.

Angenommen, wir haben einen bestimmten Benutzer und einen Dienst. Ein Dienst überträgt Zahlungen, beispielsweise in Bitcoins, mit einer bestimmten Häufigkeit an einen Benutzer. Sowohl der Benutzer als auch der Dienst sind daran interessiert, für jede Zahlung eine neue Adresse zu verwenden, um es einem externen Beobachter zu erschweren, eine Tatsache festzustellen und die Geschichte der Interaktion miteinander zu verwechseln.

Im einfachsten Fall würde es so aussehen: Der Benutzer generiert für jede eingehende Zahlung ein neues Schlüsselpaar, berechnet die Adresse, die er an den Dienst übergibt, wonach der Dienst eine Transaktion generieren und die Zahlung ausführen kann. Dies ist jedoch für beide Parteien unpraktisch, wenn die Intensität dieser Zahlungen hoch ist.

Erweiterter öffentlicher Schlüssel

In einer ähnlichen Situation hilft der erweiterte öffentliche Schlüssel (xPubKey), die Unannehmlichkeiten zu beseitigen. Der Benutzer kann einem Drittanbieter-Dienst ermöglichen, Adressen anstelle von sich selbst zu generieren, die dem Dienst bekannt sind, aber nur der Benutzer verfügt über private Schlüssel. Der Dienst kann ohne Wissen des Benutzers eine beliebige Anzahl von Adressen generieren und Geld an diese senden, und der Benutzer kann nach Belieben private Schlüssel bereitstellen und Zugriff auf eine dieser Adressen erhalten.

Wie funktioniert es Der Benutzer muss ein neues Konto auf der zweiten Ebene der Schlüsselhierarchie erstellen und für ihn den öffentlichen Schlüssel und den Kettencode für die aktuelle Ebene berechnen. Danach müssen Sie sowohl den öffentlichen Schlüssel als auch den Kettencode an den Dienst übertragen. Der Einfachheit halber wurde die Base58Check-Codierung eingeführt, über die wir gesprochen haben (hier gibt es eine spezielle Version). Als nächstes werden der öffentliche Schlüssel, der Kettencode und die Prüfsumme verkettet. Dies alles ist im Basisnummernsystem 58 codiert und wir erhalten einen öffentlichen erweiterten Schlüssel, der bereits nach einem bestimmten Standard codiert ist. Es beginnt mit den Zeichen „xpub“, die leicht zu erkennen sind. Es sieht aus wie im Bild gezeigt.



Ein Dienst kann einen solchen Schlüssel akzeptieren und öffentliche Schlüssel für den Benutzer über BIP32 bereitstellen, Adressen von ihm empfangen und dafür bezahlen. Es kann jedoch nur der Benutzer die entsprechenden privaten Schlüssel berechnen.

Gehärtete Ableitung

Bei der hierarchischen Generierung von Schlüsseln gibt es eine gehärtete Ableitung. Dies ist ein Ansatz, der die Berechnung von untergeordneten öffentlichen Schlüsseln aus dem entsprechenden übergeordneten öffentlichen Schlüssel nicht zulässt. Dies unterscheidet sich von der normalen Generierung darin, dass wir darin die Verkettung des serialisierten Punkts als übergeordneten öffentlichen Schlüssel als Nachricht an die HMAC-Funktion verwenden und bei der gehärteten Ableitung die Serialisierung des übergeordneten privaten Schlüssels verwenden.

Außerdem ist die Indexberechnung anders. Der Index bei der normalen Generierung wird direkt auf 32 Bit serialisiert und bei der gehärteten Ableitung leicht konvertiert: Es wird ein konstanter Wert hinzugefügt $$$2 ^ {31}$Dadurch wird das höchstwertige Bit auf 1 gesetzt (es wird leicht, zwischen Ableitungstypen zu unterscheiden). Dementsprechend ist der Raum der Varianten möglicher Schlüssel sowohl für die normale Erzeugung als auch für die gehärtete Ableitung gleich und gleich $$$2 ^ {31}$.



Mit einem übergeordneten öffentlichen Schlüssel und einer gehärteten Ableitung ist es daher nicht möglich, untergeordnete öffentliche Schlüssel zu berechnen. Wenn der Angreifer den übergeordneten öffentlichen Schlüssel erhält, kann er die untergeordneten Schlüssel nicht berechnen. Daher können die Adressen und ihre Beziehung zum empfangenen übergeordneten Schlüssel nicht berechnet werden. Im Falle einer normalen Ableitung, dh im Üblichen, kann eine solche Funktion verwendet werden und die Beziehung von Adressen untereinander verfolgen.

Wege der Generation

Lassen Sie uns darüber sprechen, wie Schlüssel generiert werden können.



Auf jeder Hierarchieebene gibt es einen spezifischen Index, der Aspekte der Schlüsselgenerierung definiert. Der Pfad vom Hauptschlüssel zum endgültigen Schlüssel kann durch Schrägstriche als Indizes geschrieben werden. Wenn es sich um einen privaten Schlüssel handelt, beginnt die Aufnahme mit einem kleinen „m“, und wenn wir über das Generieren eines öffentlichen Schlüssels sprechen, dann mit einem großen „M“. Wenn der Index durch ein Apostroph angezeigt wird, sollte verstanden werden, dass es sich um eine gehärtete Ableitung ohne Apostroph handelt - normale Ableitung.

Betrachten Sie einen der gängigen Schlüsselgenerierungspfade in BIP32, in denen hierarchische Schlüssel definiert wurden.



Es wird ein Pfad verwendet, in dem der Hauptschlüssel die Null-Ebene der Hierarchie ist. Im Folgenden sind die Kontenindizes aufgeführt, die denselben Benutzer bestimmen, gefolgt von Ketten, in denen Adressketten außerhalb veröffentlicht werden können, um eingehende Zahlungen zu akzeptieren. Mit Index 1 werden die Ketten erstellt, an die der Benutzer Zahlungen an sich selbst sendet (häufiger) das alles ist Kapitulation). Der endgültige Index wird verwendet, um die Schlüssel zu generieren, aus denen die Adressen berechnet werden.

Um den allerersten Schlüssel mit Index 0 gemäß dem BIP32-Standard zu berechnen, haben wir m, 0 mit der Erzeugung von gehärtet, Kette - 0, Index - 0 (m / 0 '/ 0/0). So erhalten wir den Pfad für den ersten hierarchisch generierten Schlüssel.

Es gibt einen Vorschlag zur Verbesserung von Bitcoin, der als BIP43 bezeichnet wird. Dabei wird die Verbesserungsnummer, die einen neuen Spawn-Pfad (m / bip_number '/ *) bietet, auf die erste Ebene der Hierarchie geschrieben.



So erschien BIP44, das das Merkmal des vorherigen Satzes verwendete, dh der Index 44 wurde für die erste Hierarchieebene geschrieben und schlug die folgenden Verbesserungen vor: Notieren Sie im Index der zweiten Hierarchieebene einen bestimmten Wert, der dem Münztyp entspricht, den wir für diese Brieftasche verwenden. Jetzt können Schlüssel für verschiedene Währungen in einer Brieftasche bereitgestellt und verwendet werden.



Für Bitcoin sieht der Pfad wie folgt aus: "m / 44 '/ 0' / 0 '/ 0/0", für Bitcoin testnet - "m / 44' / 1 '/ 0' / 0/0", für Litecoin - "m / 44 '/ 2' / 0 '/ 0/0 ”für Dash -“ m / 44' / 5 '/ 0' / 0/0 ”. Interessanterweise verwendet Ethereum genau die gleiche elliptische Kurve für die Berechnung der Schlüssel und die digitale Signatur. Für die Brieftasche sieht der Pfad wie folgt aus: „m / 44 '/ 60' / 0 '/ 0/0“.

Es gibt noch eine weitere Verbesserung - BIP45. Die Verbesserung zielt darauf ab, die Regeln zum Generieren von Schlüsseln für den Fall ihrer Verwendung in Multisignatur-Geldbörsen und die Bildung von Adressen unter Verwendung von BIP16, d. H. P2SH, zu bestimmen. Es enthält den BIP43-Satz und gibt den Index 45 auf der ersten Ebene der Hierarchie an, auf der zweiten Ebene der Hierarchie muss ein Unterzeichner (Mitunterzeichner) angegeben werden.



Beispielsweise gibt es eine 3-aus-5-Mehrfachsignaturregel. Daher gibt es 5 Unterzeichner, aber um Münzen auszugeben, benötigen Sie mindestens 3 Unterschriften. Somit verfügt jeder der Unterzeichner über eine HD-Brieftasche mit einem eigenen Master-Seed und gibt seine Seriennummer auf seinem Weg an. Sie kann als Index berechnet werden, wenn die auf der ersten Hierarchieebene jedes Benutzers generierten Schlüssel sortiert werden. Angenommen, auf der ersten Ebene generiert jeder Benutzer Schlüssel, tauscht sie miteinander aus, sortiert und findet heraus, wer welchen Index für die zweite Ebene der Hierarchie hat. Dies ist erforderlich, um die Notwendigkeit einer solchen Interaktion weiter zu beseitigen und sofort Adressen korrekt zu generieren und Ihre Seriennummer zu kennen.

Das heißt, Sie können den erweiterten öffentlichen Schlüssel einmal austauschen, um unabhängig von anderen Mitgliedern der Gruppe Multisignaturadressen zu bilden und Zahlungen für diese zu akzeptieren.

Fragen

Kommen wir zu häufig gestellten Fragen.

- Wie unterscheiden sich Mastersamen in verschiedenen Münzen?

Seed ist eine zufällig generierte Zahl, eine Folge von Bits oder eine Mnemonikphrase, die beispielsweise gemäß BIP39 generiert wird und zum Generieren von Schlüsseln verwendet wird. Es kann sowohl für eine Münze als auch für jede andere verwendet werden - es ist nicht erforderlich, unterschiedliche Mnemonikphrasen für unterschiedliche Währungen zu verwenden. Darüber hinaus gibt es BIP44, das die Regeln zum Generieren von Schlüsseln für verschiedene Währungen aus derselben Mnemonik definiert. Diese privaten Schlüssel überschneiden sich nicht, sondern werden für verschiedene Adressen verschiedener Währungen verwendet.

- Wörterbuch aus BIP39, in dem 2048 Wörter für eine mnemonische Phrase standardisiert sind? Kann ich es in allen Geldbörsen und Anwendungen verwenden?

Tatsache ist, dass dieser Standard für BIP39 beschrieben ist. Für BIP39 gibt es Wörterbücher: Englisch, zwei Japanisch, Chinesisch, Italienisch, Russisch, Ukrainisch usw. Wenn also eine Anwendung behauptet, BIP39 zu verwenden und das Importieren und Exportieren einer Mnemonikphrase zu ermöglichen, bedeutet dies, dass auch eine Reihe von Wörtern verwendet wird das gleiche. Es gibt jedoch Brieftaschen, die nicht BIP39 verwenden, sondern ihre eigene Modifikation. Sie müssen sich die Brieftaschenbeschreibung ansehen und entweder standardisierte oder Ihre eigene Entwicklung oder die Entwicklung des Dienstes verwenden, den die Brieftasche bietet.

- Werden bei Börsen und zentralisierten Speichern wie Coinbase die Brieftaschenschlüssel für alle Benutzer aus derselben gemeinsamen Phrase für alle generiert oder nicht?

Es ist schwer zu sagen, da sie ihre interne Struktur nicht öffnen, aber die neuen Dienste, die angezeigt werden, können entweder separat Schlüssel generieren oder den BIP32-Standard verwenden oder seine modifizierte Version verwenden. Die Dienste, die vor dem Erscheinen der Standards für die hierarchische Schlüsselgenerierung existierten, generieren höchstwahrscheinlich weiterhin nur separate private Schlüssel. Vielleicht sind sie so einfacher zu verwalten, wenn alle Schlüssel einen großen Umsatz haben.

"Ist der Schlüssel ein Punkt auf der elliptischen Kurve, dh zwei sehr große Zahlen X und Y?"

Der öffentliche Schlüssel - ja, dies ist ein Punkt auf der elliptischen Kurve, und der private Schlüssel ist eine natürliche Zahl, die angibt, wie oft Sie den Basispunkt mit sich selbst hinzufügen müssen. Der öffentliche Schlüssel selbst besteht aus zwei Werten - dies sind die X- und Y-Koordinaten, von denen jeder eine Größe von 256 Bit hat.

- Was ist "Cast to Point" und Serialisierung von Punkt und Index?

Reduktion auf einen Punkt bedeutet, dass es eine natürliche Zahl gibt, die wir als privaten Schlüssel betrachten. Wir addieren den Basispunkt so oft mit uns selbst, dh in der Gruppe der Punkte auf der elliptischen Kurve wird nur die Additionsoperation definiert, dann können wir den Punkt mit einer natürlichen Zahl multiplizieren. Die Serialisierung eines Punktes bedeutet, auf eine bestimmte Weise zwei Koordinaten aufzuzeichnen. Dies kann ein komprimierter Datensatz sein, ist jedoch nicht erforderlich. Komprimiert in dem Sinne, dass eine der Koordinaten, nämlich Y, in ein Vorzeichen umgewandelt wird, werden die Daten in die Gleichung eingesetzt und es wird untersucht, wo sich der Punkt befindet: oben oder unten. Bei der Indexserialisierung müssen Sie verstehen, dass eine reguläre Zahl, die je nach Größe in Bytes oder Bits geschrieben werden kann. Je größer die Anzahl, desto mehr Daten werden benötigt. Bei den von uns untersuchten Berechnungeneine Nummer einer bestimmten Länge ist erforderlich. Sie müssen es auf eine bestimmte Länge serialisieren - 4 Bytes. Infolgedessen bezieht sich dies auf das Umwandeln des Index in eine 4-Byte-Zahl. Wenn die Senior-Werte dort leer bleiben, sind sie Null.

- Wer hat diese Berechnungen für die Ableitungsfunktionen von HD-Geldbörsen erstellt? Warum solche Formeln, in denen es Rechtfertigungen gibt und in denen Sie mehr darüber lesen können?

Sie können mehr in BIP32 lesen, wenn Sie an einer Mnemonik interessiert sind, dann in BIP39 usw. Sie können GitHub öffnen und einen Benutzer unter dem Spitznamen Bitcoin finden. Er verfügt über ein Bitcoin-Repository, in dem der Bitcoin-Quellcode gespeichert ist, und über ein BIPs-Repository (primäre Quelle), in dem alle Vorschläge zur Verbesserung von Bitcoin aufgezeichnet sind.

Sie kamen auf die Idee, Berechnungen auf diese Weise durchzuführen, da sie an eine Gruppe von Punkten einer elliptischen Kurve gebunden sind. Wenn Sie eine solche Funktionalität erreichen möchten, mit der Sie die Zweige öffentlicher und privater Schlüssel getrennt berechnen und gleichzeitig ihre Korrespondenz untereinander aufrechterhalten können, war dies die einfachste Implementierungsoption. Tatsächlich verwendeten die Entwickler die einfachste Option, mit der Sie mithilfe der im Laufe der Zeit getesteten Kryptografie interessante Eigenschaften erzielen können. Die Autoren der vorgeschlagenen Verbesserungen sind viele. Die Bitcoin-Community, deren Teilnehmer Verbesserungen und mathematische Transformationen entwickeln, ist ziemlich groß.

- Gehärtete Ableitung ist immer nur auf der zweiten Ebene der Hierarchie?

Es hängt alles von der Situation ab. Bei der Generierung von Schlüsseln für die Mehrfachsignatur ist es sinnvoll, eine gehärtete Ableitung nur auf der ersten Hierarchieebene durchzuführen. In BIP44 wird die gehärtete Ableitung auf die ersten drei Ebenen angewendet: Auf der ersten Ebene ist die Nummer des BIP selbst, auf der zweiten die Kontonummer, wo sie relevant ist, auf der dritten die Währungsnummer, wo sie ebenfalls sinnvoll ist. Angenommen, es wird Ihnen wahrscheinlich nicht gefallen, wenn Sie den öffentlichen Schlüssel veröffentlichen, und die Benutzer können alle Ihre Adressen in Bitcoin verfolgen. Wenn Sie ein Konto verwenden, um Zahlungen von bestimmten Diensten zu erhalten, können Sie diesen Schlüssel offenlegen, und Sie benötigen hier keine gehärtete Ableitung.

- Wo kann die hierarchische Schlüsselgenerierung angewendet werden?

Sie können es anwenden, wenn Sie mit der Börse arbeiten, sodass die Börse Sie immer an verschiedene Adressen bezahlt. In diesem Fall ist es jedoch besser, dies alles manuell zu organisieren. Dies ist für alltägliche digitale Geldbörsen am relevantesten, da es hier sehr einfach ist, eine Sicherung privater Schlüssel zu erstellen und eine Geldbörse wiederherzustellen. Die Schlüsselgenerierung für verschiedene Währungen wird ebenfalls unterstützt, und der Standard selbst wird bereits in verschiedenen Implementierungen digitaler Geldbörsen verwendet. Die Schlüssel zwischen diesen Brieftaschen lassen sich bequem mit derselben Mnemonik übertragen.

Dieses Thema wird in einer der Vorlesungen des Online-Blockchain-Kurses „ Hierarchical Key Generation “ behandelt.