Einführung
Um die ballistisch-zeitlichen Eigenschaften der Bewegung des Massenschwerpunkts des Fallschirmjägers zu bestimmen, muss ein vereinfachtes mathematisches Modell gewählt werden, das für die analytische Forschung leicht zugänglich ist und gleichzeitig die charakteristischsten Merkmale des ursprünglichen Objekts beibehält.
Um vereinfachte mathematische Modelle der Bewegung des Fallschirmjägers zu erstellen, wird eine Analyse, Bestimmung, Systematisierung von Konstanten- und Zeitparametern durchgeführt.
Regelmäßige und hinreichend begründete Methoden zur Konstruktion nichtlinearer mathematischer Modelle existieren derzeit nicht. Zur Lösung bestimmter Probleme können jedoch bei korrekter Zusammensetzung der Anfangssysteme nichtlinearer Differentialgleichungen numerische Methoden zu deren Lösung durchaus adäquate Ergebnisse liefern.
Der Zweck dieser Veröffentlichung ist die Zusammenstellung und numerische Lösung von Differentialgleichungssystemen, die alle Stadien der Bewegung eines Fallschirmjägers beschreiben, der aus einem Flugzeug landet, wobei die Auswirkungen von Änderungen der Höhe und Temperatur der Luftmassendichte berücksichtigt werden.
Ballistisch-zeitliche Merkmale der Bewegung eines Fallschirmjägers
Konstante und begrenzte variable Parameter umfassen:
H - die Höhe der Freilassung des Fallschirmjägers;
V0 - Flugzeuggeschwindigkeit;
k - Gewicht, Größe des Fallschirmjägers;
g ist die Erdbeschleunigung;
ρ ist die Luftdichte;
T ist die Lufttemperatur.
Temporäre (variable) Parameter umfassen:
tn - Landezeit,
w ist die Windgeschwindigkeit;
V ist die Geschwindigkeit des Fallschirmjägers;
u ist die Geschwindigkeit der aufsteigenden (absteigenden) Strömungen;
d - Drift (Abstand von der Projektion auf den Boden des Auswurfpunkts zum Aufsetzpunkt);
C ist der Luftwiderstandsbeiwert des Landeobjekts;
F - Mittelteil des Landeobjekts.
Sprungstufen
Die erste Stufe ist ein freier Fall nach der Trennung vom Flugzeug:
 Die zweite Stufe
Die zweite Stufe ist eine Abnahme eines stabilisierenden Fallschirms:

Die Haupteigenschaft des stabilisierenden Fallschirms ist die Stabilisierung des Fallschirmspringers in der für den Hauptfallschirm am besten geeigneten Position.
Die dritte Stufe - Füllen der Kuppel des Hauptfallschirms:
 Die vierte Stufe
Die vierte Stufe ist eine Abnahme des offenen Fallschirms:

Zusammenstellung eines Differentialgleichungssystems für alle Stufen eines Fallschirmsprungs
Wir wählen ein festes Koordinatensystem OXY, das am Auswurfpunkt O zentriert ist. Die Achse OX fällt mit der Richtung der horizontalen Komponente der Flugzeuggeschwindigkeit zusammen. Die OY-Achse ist in entgegengesetzter Richtung zur Vertikalgeschwindigkeit des Fallschirmspringers vertikal nach oben gerichtet.
Wir gehen davon aus, dass die Bewegung des Fallschirmjägers flach ist und in der OXY-Ebene stattfindet. Dieses Modell eines Sprunges kann als Modell eines Sprunges bei ruhigem Wetter betrachtet werden, ohne den Einfluss des Windes zu berücksichtigen.
Wir glauben, dass der Fallschirmjäger zusätzlich zum Gewicht von der Luftwiderstandskraft beeinflusst wird, die proportional zum Quadrat der Geschwindigkeit des Fallschirmjägers ist:
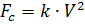
,
wo:
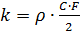
,
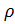
- Luftdichte, C - Luftwiderstandsbeiwert, F - Mittelteil des Körpers.
Mit zunehmender Höhe ändert sich die Lufttemperatur:

Die Mindesttemperatur wird bereits in 10 km Höhe erreicht. und ist -55 ° C. Die Luftdichte hängt auch vom Druck ab. Daher ist es bei der Berechnung der Ballistik eines Fallschirmsprungs zweckmäßig, die folgende Formel zur Bestimmung der Luftdichte zu verwenden [1]:
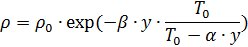
,
wo
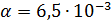
K / m;
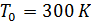
- Temperatur auf Meereshöhe; y ist die Höhe in m;

- Luftdichte bei y = 0;
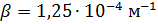
.
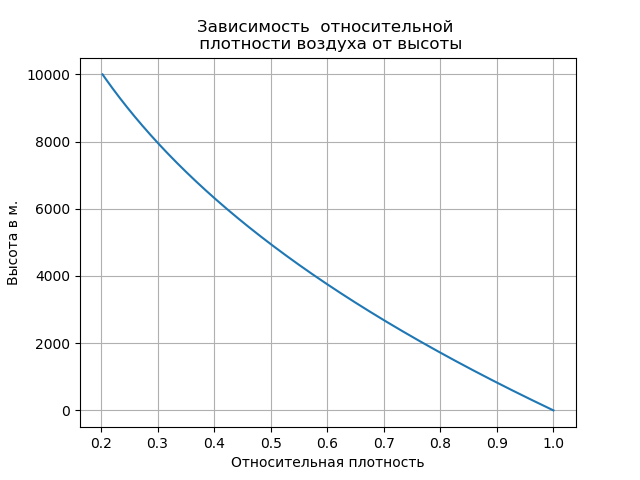
In der Praxis der Berechnungen wird das Wachstumsquadrat als Mittelteil genommen; Der Wert von C ergibt sich aus der Tabelle [2]:

Θ bezeichnet den Neigungswinkel der Flugbahn. Unter den für die Komponenten getroffenen Annahmen
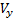
,
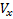
Geschwindigkeitsvektoren V haben wir:

Teilen der linken und rechten Seite der Gleichungen des resultierenden Systems durch m und Bezeichnen

durch r bekommen wir:
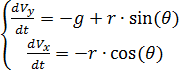
(1)
Wir schreiben die Bewegungsgleichungen eines Fallschirmspringers in Form eines Differentialgleichungssystems für die Funktionen V, θ, y (t), x (t) auf.
Vorausgesetzt, dass:
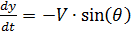
,
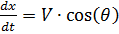
,
und Differenzierungszeitverhältnis:

unter Berücksichtigung des Gleichungssystems (1) erhalten wir:
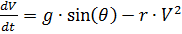
,
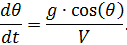
.
Also unter den Anfangsbedingungen:
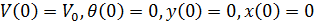
Wir haben das folgende System von Differentialgleichungen:
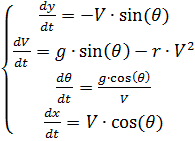
Numerische Lösung eines Differentialgleichungssystems (2) mit Python
Um (2) zu lösen, schreiben wir es in der folgenden Form um und führen stabilisierende Widerstandskräfte ein, die durch Zeit und Luftdichte gesteuert werden
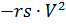
und main
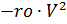
Fallschirme multipliziert mit den Zeitsteuerungsfunktionen ks (t) und ko (t):
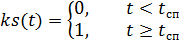
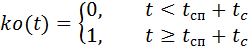
,
wo:
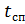
–– Zeit des freien Falls des Fallschirmjägers;

- die Betriebszeit des Stabilisierungsfallschirms bis zum Öffnen des Hauptfallschirms.
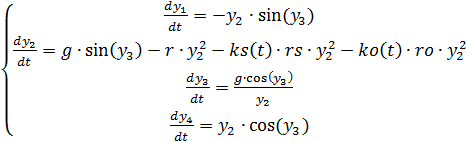
(3)
Vollständige Auflistung des Programms, angepasst an Änderungen der Luftdichte Wir bekommen:
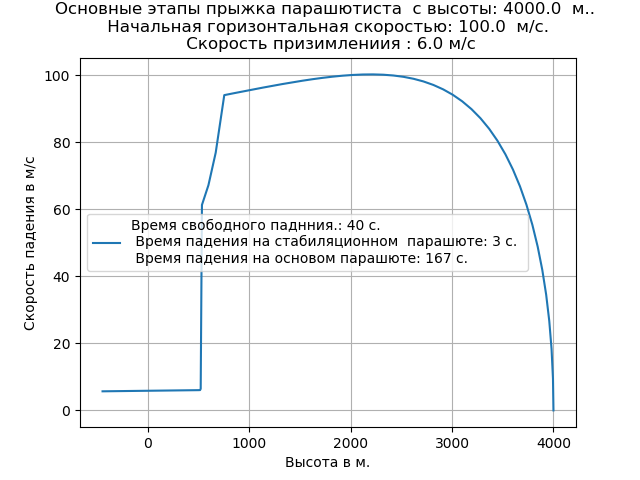
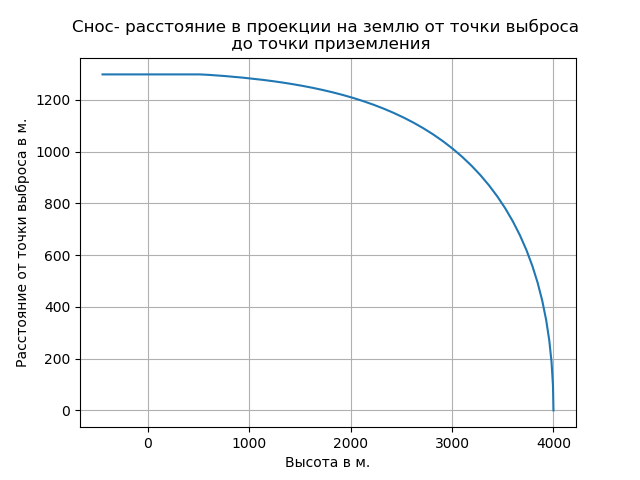
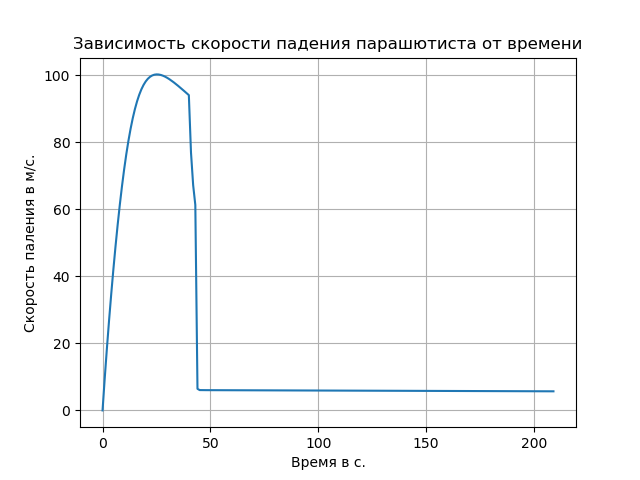
Die Berücksichtigung der verdünnten Luft führte zu einer Erhöhung der freien Fallrate und veränderte die Art der Flugbahn in diesem Abschnitt.
Dieses Problem kann mit Hilfe eines Systems von zwei Differentialgleichungen gelöst werden, die unten angegeben sind (ausgenommen Fallschirme und Änderungen der Luftdichte):
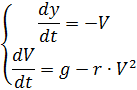
Die Änderung der Widerstandskräfte und der Luftdichte ist in der Auflistung unter dem Spoiler unter Berücksichtigung der obigen und ohne Erklärung angegeben# - * - Kodierung: utf8 - * -
von numpy import *
von scipy.integrate import odeint
importiere matplotlib.pyplot als plt
m = 100
r0 = 1,3
c1 = 0,3
c2 = 0,6
c3 = 0,5
c4 = 0,75
S = 70
s = 0,8
ss = 1,5
g = 9,8
TL = 6
tsbp = 10
tp = 90,0
h = 1000,0
Beta = 1,25 * 10 ** - 4
alfa = 6,5 * 10 ** - 3
T0 = 300
def ks (t):
wenn t <tsp:
z = 0
sonst:
z = 1
return z
def ko (t):
wenn t <tsp + tsbp:
z = 0
sonst:
z = 1
return z
# dy1 / dt = y2
# dy2 / dt = g- (k1 · y2 ** 2) / m- (k2 · y2) / m- (ks (t) · k3 · y2 ** 2) / m- (ko (t) · k4 * y2 ** 2) / m
def f (y, t):
y1, y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0,5 * r * c1 * s
k2 = 0,5 * r * c2 * s
k3 = 0,5 * r * c3 * ss
k4 = 0,5 * r * c4 * S.
Rückgabe [-y2, g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m]
t = Bereich (0,0, tp)
y0 = [h, 0,0]
[y1, y2] = odeint (f, y0, t, full_output = False) .T
plt.title ("Fallschirmspringen aus 1000 und 800 Metern")
plt.plot (y1, y2, label = 'Höhe 1000 m')
h = 800,0
TL = 6
tsbp = 2
tp = 80,0
def ks (t):
wenn t <tsp:
z = 0
sonst:
z = 1
return z
def ko (t):
wenn t <tsp + tsbp:
z = 0
sonst:
z = 1
return z
def f (y, t):
y1, y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0,5 * r * c1 * s
k2 = 0,5 * r * c2 * s
k3 = 0,5 * r * c3 * ss
k4 = 0,5 * r * c4 * S.
Rückgabe [-y2, g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m]
t = Bereich (0,0, tp)
y0 = [h, 0,0]
[y1, y2] = odeint (f, y0, t, full_output = False) .T
plt.plot (y1, y2, label = 'Höhe 800 m')
plt.xlabel ('Höhe in m.')
plt.ylabel ('Brenngeschwindigkeit in m / s.')
plt.legend (loc = 'best')
plt.grid (True)
plt.show ()
Wir bekommen:

Fazit
Die ballistisch-zeitlichen Eigenschaften der Bewegung des Massenschwerpunkts einer Fallschirmjägerlandung aus einem Flugzeug werden bestimmt.
Referenzen
- Atmosphärendruck.
- Gerasimenko I.A. Flugtraining: Lehrbuch. M.: Military Publishing, 1986. Teil 1, S. 32.