Reduktion des neuronalen Netzes durch Variationsoptimierung

Hallo Habr. Heute möchte ich das Thema Variationsoptimierung entwickeln und erläutern, wie es auf die Aufgabe angewendet werden kann, nicht informative Kanäle in neuronalen Netzen zu beschneiden (Bereinigen). Mit ihm kann man die "Feuerrate" eines neuronalen Netzwerks relativ leicht erhöhen, ohne seine Architektur zu schaufeln.


Die Idee, redundante Elemente in Algorithmen für maschinelles Lernen zu reduzieren, ist überhaupt nicht neu. Tatsächlich ist es älter als das Konzept des tiefen Lernens: Erst früher wurden Zweige entscheidender Bäume gefällt und jetzt in einem neuronalen Netzwerk gewichtet.

Die Grundidee ist einfach: Wir finden im Netzwerk eine Teilmenge nutzloser Gewichte und setzen sie auf Null. Ohne eine umfassende Suche ist es schwierig zu sagen, welche Gewichte wirklich an der Vorhersage beteiligt sind und welche nur so tun, aber dies ist nicht erforderlich. Verschiedene Regularisierungsmethoden, Optimal Brain Damage und andere Algorithmen funktionieren gut. Warum überhaupt Gewichte entfernen? Es stellt sich heraus, dass dies die Generalisierungsfähigkeit des Netzwerks verbessert: In der Regel führen unbedeutende Gewichte entweder einfach Rauschen in die Vorhersage ein oder werden speziell für Anzeichen eines Trainingsdatensatzes (d. H. Ein Artefakt der Umschulung) geschärft. In diesem Sinne kann die Reduzierung von Verbindungen mit der Methode zum Trennen zufälliger Neuronen (Dropout) während des Netzwerktrainings verglichen werden. Wenn das Netzwerk viele Nullen hat, nimmt es außerdem weniger Speicherplatz im Archiv ein und kann auf einigen Architekturen schneller lesen.

Es hört sich gut an, aber es ist viel interessanter, nicht separate Gewichte, sondern Neuronen aus vollständig verbundenen Schichten oder Kanälen aus den gesamten Bündeln herauszuwerfen. In diesem Fall wird der Effekt der Netzwerkkomprimierung und Beschleunigung von Vorhersagen viel deutlicher beobachtet. Dies ist jedoch komplizierter als die Zerstörung einzelner Gewichte: Wenn Sie versuchen, den optimalen Hirnschaden auszuführen und das gesamte Bündel anstelle einer Verbindung zu verwenden, sind die Ergebnisse wahrscheinlich nicht sehr beeindruckend. Um ein Neuron schmerzlos entfernen zu können, muss es so hergestellt werden, dass es keine einzige nützliche Verbindung hat. Um dies zu tun, müssen Sie irgendwie "starke" Neuronen dazu bringen, stärker und "schwache" Neuronen schwächer zu werden. Diese Aufgabe ist uns bereits bekannt: Tatsächlich erzwingen wir, dass das Netzwerk sparsam ist, mit einigen Einschränkungen bei der Gruppierung von Gewichten.

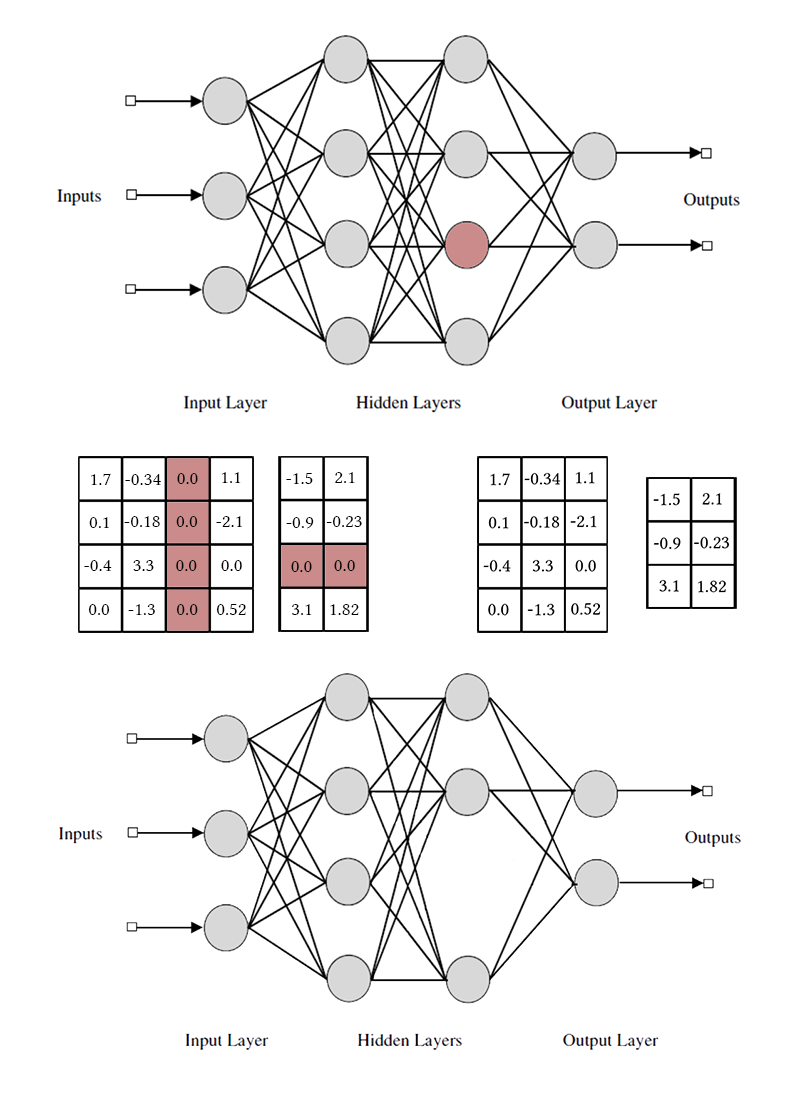
Beachten Sie, dass Sie zwei Gewichtsmatrizen ändern müssen, um ein Neuron oder einen Faltungskanal zu entfernen. Ich werde nicht zwischen Faltungskanälen und Neuronen unterscheiden: Die Arbeit mit ihnen ist dieselbe, nur die spezifischen entfernten Gewichte und die Transpositionsmethode unterscheiden sich.

Der einfache Weg: Regularisierung der Gruppe L1

Zunächst erzähle ich Ihnen, wie Sie am einfachsten und effektivsten zusätzliche Neuronen aus dem Netzwerk entfernen können - die Gruppen-LASSO-Regularisierung. Am häufigsten wird es verwendet, um nutzlose Gewichte in Netzwerken nahe Null zu halten. es verallgemeinert sich trivial auf den Fall von Kanal zu Fall. Im Gegensatz zur regulären Regularisierung regulieren wir das Gewicht oder die Schichtaktivierung nicht direkt, die Idee ist etwas kniffliger. [Channel Pruning zur Beschleunigung sehr tiefer neuronaler Netze; Yihui He et al.; 2017]

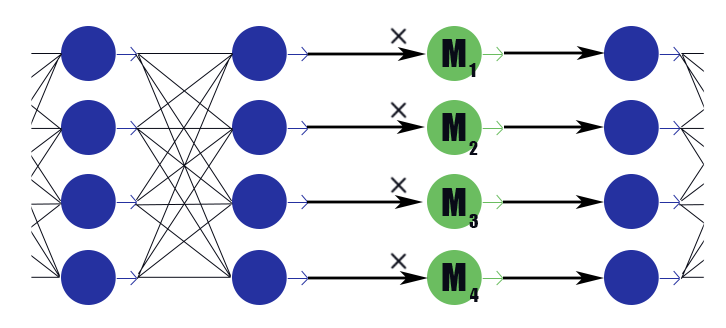
Betrachten Sie eine spezielle Maskenebene mit einem Gewichtsvektor $$$M = (\ beta_1, \ beta_2, \ dots, \ beta_n)$. Sein Fazit ist nur eine stückweise Arbeit $$$M$Nach den Schlussfolgerungen der vorherigen Schicht hat er keine Aktivierungsfunktion. Wir platzieren in der Maskierungsschicht nach jeder Schicht die Kanäle, in denen wir verwerfen möchten, und unterziehen die Gewichte in diesen Schichten einer L1-Regularisierung. Also das Gewicht der Maske $$$\ beta_i$multipliziert mit der i-ten Ausgabe der Schicht bedeutet dies implizit eine Beschränkung aller Gewichte, von denen diese Schlussfolgerung abhängt. Wenn unter diesen Gewichten die Hälfte nützlich ist, dann $$$beta_i$wird näher an der Einheit bleiben, und diese Schlussfolgerung wird in der Lage sein, Informationen gut zu übertragen. Aber wenn nur einer oder gar keiner, $$$beta_i$es wird auf Null fallen, wodurch die Ausgabe des Neurons zurückgesetzt wird und tatsächlich alle Gewichte zurückgesetzt werden, von denen diese Schlussfolgerung abhängt (im Fall der Aktivierungsfunktion gleich Null bei Null). Bitte beachten Sie, dass das Netzwerk auf diese Weise im Falle eines rechtlich hohen Gewichts oder einer rechtlich starken Reaktion weniger negative Verstärkung erhält. Die Nützlichkeit des Neurons als Ganzes ist wichtig.

Es stellt sich diese Formel heraus:

Wo $$$\ lambda$- Gewichtungskonstante von Verlust eines Netzwerks und Verlust einer Spärlichkeit. Es sieht aus wie die übliche L1-Regularisierungsformel, nur der zweite Term enthält Vektoren von Maskierungsschichten und nicht das Gewicht des Netzwerks.

Nach dem Training des Netzwerks gehen wir die Neuronen und ihre Maskierungswerte durch. Wenn $$$beta_i$mehr als eine bestimmte Schwelle, dann werden die Neuronengewichte mit multipliziert $$$beta_i$Wenn weniger, werden die dem Neuron entsprechenden Elemente aus den Matrizen der eingehenden und ausgehenden Gewichte entfernt (wie im Bild etwas höher). Danach können die Masken gelöscht und das Netzwerk abgeschlossen werden.

In der Anwendung der Gruppe LASSO gibt es mehrere Feinheiten:

1. Normale Regularisierung. Zusammen mit der Regularisierung der Maskengewichte sollte die L1 / L2-Regularisierung auf alle anderen Netzwerkgewichte angewendet werden. Ohne dies wird eine Abnahme des Maskierungsgewichts bei ungesättigten Aktivierungsfunktionen (ReLu, ELu) leicht durch eine Zunahme der Gewichte kompensiert, und der Nullungseffekt funktioniert nicht. Ja, und für gewöhnliche Sigmoid können Sie den Prozess besser mit positivem Feedback beginnen: $$$M_i$Die nicht informative Ausgabe wird kleiner, weshalb der Optimierer stärker über jedes spezifische Gewicht nachdenken muss, was die Ausgabe noch uninformativer macht, weshalb $$$M_i$nimmt noch mehr ab und so weiter.
2. Die Autoren des Artikels raten auch, das Gewicht der Schichten sphärisch zu beschränken $$$| W_i | _2 = 1$. Dies sollte wahrscheinlich zum „Fluss“ des Gleichgewichts von schwachen zu starken Neuronen beitragen, aber ich bemerkte keinen großen Unterschied.
3. Push-Pull-Training. Die Autoren des Artikels schlagen vor, abwechselnd die Normalgewichte des neuronalen Netzwerks zu trainieren und die Gewichte zu maskieren. Es ist länger als alles gleichzeitig zu unterrichten, aber als ob die Ergebnisse etwas besser wären?
4. Vergessen Sie nicht die lange Feinabstimmung des Netzwerks (Feinabstimmung) nach dem Fixieren der Maske, dies ist sehr wichtig.
5. Überwachen Sie sorgfältig, wie Ihre Masken stehen: vor oder nach der Aktivierungsfunktion. Möglicherweise haben Sie Probleme mit Aktivierungen, die nicht gleich Null sind, wenn das Argument Null ist (z. B. ein Sigmoid).
6. Das Bereinigen ist mit Batchnorm aus dem gleichen Grund nicht freundlich, aus dem Dropout nicht mit Batchnorm befreundet ist: Aus Sicht der Normalisierung, wenn das Paket 32 ​​Werte enthält, von denen 12 Null sind, und wenn 20 Werte im Paket sehr unterschiedliche Situationen sind. Nach dem Herausreißen des Nullsaldos ist die von der Batchnorm-Schicht gelernte Verteilung nicht mehr gültig. Sie müssen entweder nach allen Batchnorm-Ebenen Schnittschichten einfügen oder letztere irgendwie ändern.
7. Es gibt auch Schwierigkeiten bei der Anwendung der Kanalreduzierung auf Verzweigungsarchitekturen und Restnetzwerke (ResNet). Nach dem Trimmen zusätzlicher Neuronen während der Fusion von Zweigen stimmen die Dimensionen möglicherweise nicht überein. Dies lässt sich leicht durch die Einführung von Pufferschichten lösen, in denen wir keine Neuronen abstoßen. Wenn die Netzwerkzweige eine unterschiedliche Informationsmenge enthalten, ist es außerdem sinnvoll, unterschiedliche Einstellungen vorzunehmen $$$\ lambda$damit sich nicht herausstellt, dass das Beschneiden nur alle Neuronen im am wenigsten informativen Zweig schneidet. Wenn jedoch alle Neuronen geschnitten sind, ist das nicht ein so wichtiger Zweig?
8. In der ursprünglichen Problemstellung gibt es eine strikte Beschränkung für die Anzahl der Kanäle ungleich Null. Meiner Meinung nach reicht es jedoch aus, nur die Gewichtungsparameter des Anfangsverlusts und des L1-Verlusts der Maskierungsgewichte zu ändern und dann den Optimierer entscheiden zu lassen, wie viele Kanäle verlassen werden sollen.
9. Masken erfassen. Dies ist nicht im Originalartikel enthalten, aber meiner Meinung nach ist dies ein guter praktischer Mechanismus zur Verbesserung der Konvergenz. Wenn der Wert der Maske einen bestimmten vorgegebenen niedrigen Wert erreicht, setzen wir ihn zurück und verbieten das Ändern dieses Teils der Maske. Daher tragen schwache Gewichte bereits während des Trainings des Modells nicht mehr zur Vorhersage bei und führen keine Streuwerte in die entsprechenden Beträge ein. Theoretisch kann dies verhindern, dass ein potenziell nützlicher Kanal wieder in Betrieb genommen wird, aber ich glaube nicht, dass dies in der Praxis geschieht.

Der harte Weg: L0-Regularisierung

Aber wir suchen nicht nach einfachen Wegen, oder?

Die Ablehnung von Kanälen mithilfe der L1-Regularisierung ist nicht ganz fair. Es ermöglicht dem Kanal, sich auf der Skala von "starke Antwort" - "schwache Antwort" - "Nullantwort" zu bewegen. Nur wenn das Maskierungsgewicht nahe genug bei Null liegt, wird der Kanal mithilfe der Erfassungsmaske verworfen. Eine solche Bewegung verzerrt das Bild erheblich und nimmt während des Trainings Änderungen an anderen Kanälen vor: Bevor sie lernen können, was zu tun ist, wenn das vorherige Neuron vollständig ausgeschaltet ist, müssen sie lernen, was zu tun ist, wenn es systematisch eine schwache Reaktion gibt.

Ich möchte Sie daran erinnern, dass wir im Idealfall eifrig den am wenigsten informativen Kanal aus dem Netzwerk auswählen, das Netzwerk ohne ihn weiter lernen, den am wenigsten informativen Kanal löschen, das Netzwerk erneut anpassen und so weiter möchten. Leider ist in einer solchen Formulierung die Aufgabe selbst für relativ einfache Netzwerke rechnerisch unerträglich. Darüber hinaus lässt dieser Ansatz den Kanälen keine zweite Chance - sobald ein entferntes Neuron nicht wieder in Betrieb gehen kann. Lassen Sie uns die Aufgabe ein wenig ändern: Manchmal entfernen wir das Neuron und verlassen es manchmal. Wenn das Neuron als Ganzes nützlich ist, bleibt es häufiger übrig, aber wenn es nutzlos ist - umgekehrt. Dafür verwenden wir die gleichen Maskierungsebenen wie bei der L1-Regularisierung (nicht ohne Grund wurden sie eingeführt!). Nur ihre Gewichte bewegen sich nicht entlang der gesamten realen Achse mit dem Attraktor bei Null, sondern konzentrieren sich um 0 und 1. Nicht, dass es viel einfacher geworden wäre, aber zumindest das Problem der kategorialen Entfernung von Neuronen gelöst.

Der Instinkt des Netzwerktrainers legt nahe, dass es nicht erforderlich ist, das Problem durch eine umfassende Suche zu lösen. Sie müssen jedoch die Anzahl der aktiven Neuronen in den Schichten des aktuellen Laufs zur Verlustfunktion hinzufügen. Ein solcher Verlustbegriff ist jedoch schrittweise konstant, und der Gradientenabstieg kann damit nicht funktionieren. Es ist notwendig, den Lernalgorithmus irgendwie zu lehren, einige Neuronen trotz des Fehlens eines Gradienten periodisch auszuschließen.

Wir haben eine Möglichkeit, Neuronen vorübergehend zu entfernen: Wir können einen Dropout auf die Maskenebene anwenden. Während des Trainings lassen $$$\ beta_i = 1$mit Wahrscheinlichkeit $$$\ pi$und $$$\ beta_i = 0$mit Wahrscheinlichkeit $$$1 - \ pi$. Jetzt können Sie in der Verlustfunktion die Summe eingeben $$$\ pi$Das ist eine reelle Zahl. Hier stehen wir vor einem weiteren Hindernis: Die Verteilung ist diskret, es ist nicht klar, wie die Rückausbreitung damit funktioniert. Im Allgemeinen gibt es spezielle Optimierungsalgorithmen, die uns hier helfen können (siehe REINFORCE), aber wir werden einen anderen Ansatz verfolgen.

Und dann kam der Moment, in dem die Variationsoptimierung ins Spiel kommt : Wir können die diskrete Verteilung von Nullen und Einsen in der Maskierungsschicht durch eine kontinuierliche Eins approximieren und deren Parameter unter Verwendung des üblichen Backpropagation-Algorithmus optimieren. Dies ist die Idee hinter der Arbeit [Lernen spärlicher neuronaler Netze durch L0-Regularisierung; Christos Louizos et al.; 2017].

Die Rolle der kontinuierlichen Verteilung wird die Verteilung von hartem Beton spielen [Die konkrete Verteilung: Eine kontinuierliche Relaxation diskreter Zufallsvariablen; Chris Maddison; 2017], hier ist eine so knifflige Sache aus den Logarithmen, die sich der Bernoulli-Verteilung annähert:

$$$\ alpha$- Versatzverteilung relativ zur Mitte und $$$\ beta$- Temperatur. Bei $$$\ beta \ rightarrow 0$Die Verteilung nähert sich immer mehr der tatsächlichen Bernoulli-Verteilung an, verliert jedoch ihre Differenzierbarkeit. Bei $$$0 <\ beta <1$Die Verteilungsdichte ist konkav (dies ist der Fall, an dem wir interessiert sind), z $$$\ beta> 1$- konvex. Wir leiten diese Verteilung durch ein starres Sigmoid, so dass es mit einer endlichen Wahrscheinlichkeit ungleich Null geschickt ausgeben kann $$$z = 0$und $$$z = 1$und im Intervall (0, 1) hatte es eine kontinuierlich differenzierbare Dichte. Nach Abschluss des Schnittes prüfen wir, in welche Richtung sich die Verteilung verschoben hat, und ersetzen die Zufallsvariable $$$z$auf einen bestimmten Maskenwert $$$\ beta$und wir bringen ein bereits deterministisches Modell auf den Zustand.

Um eine etwas bessere Verteilung zu erzielen, werde ich einige Beispiele für die Dichte für verschiedene Parameter nennen:

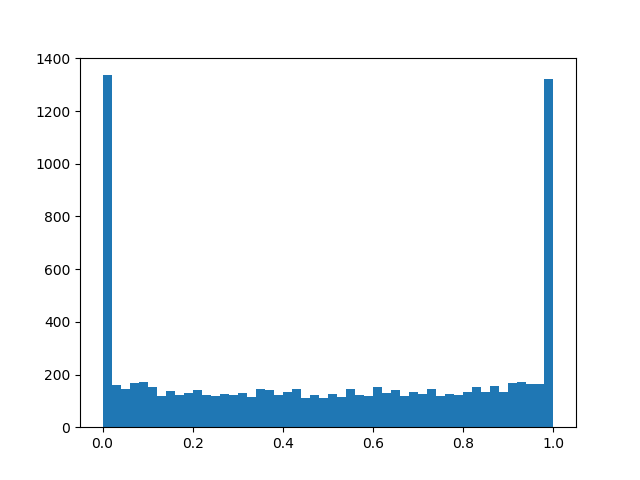
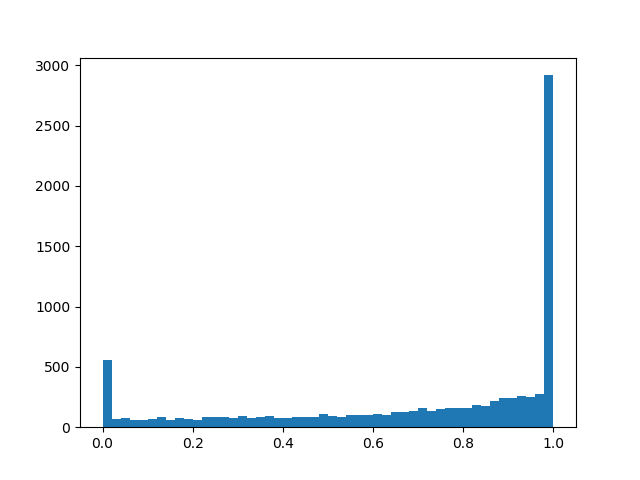
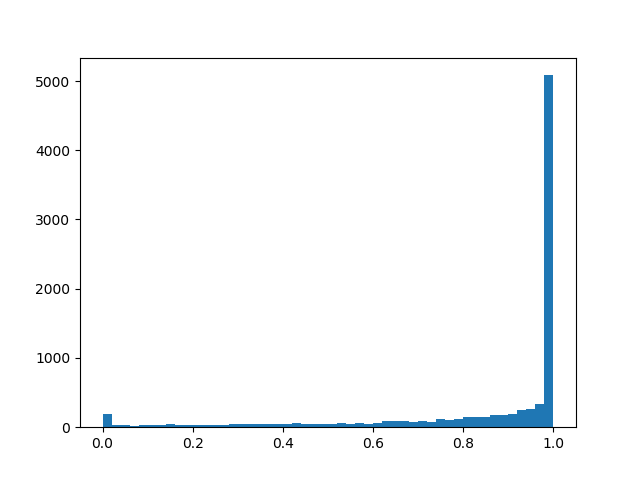
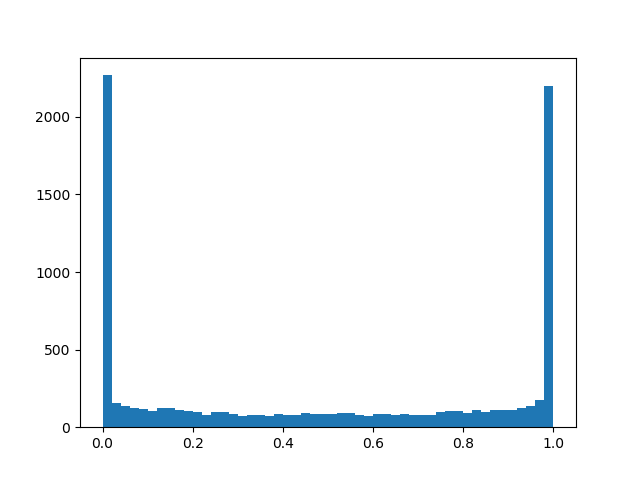
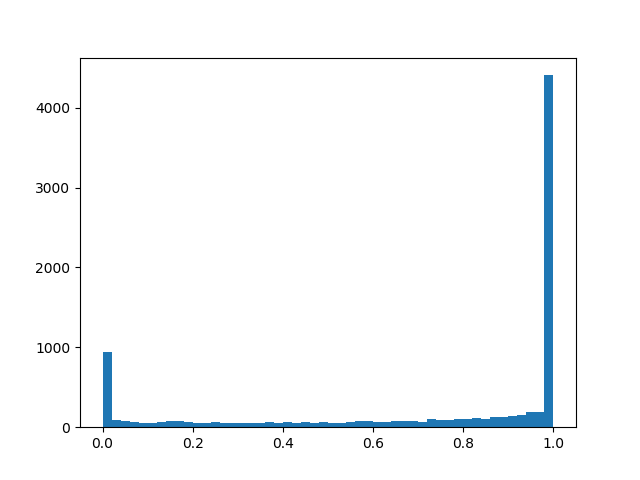
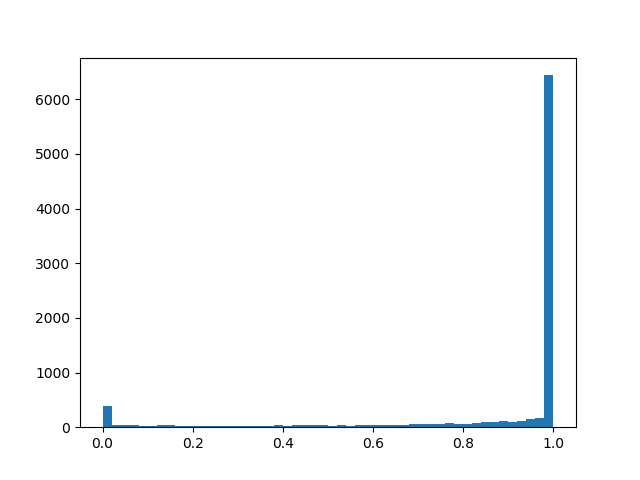
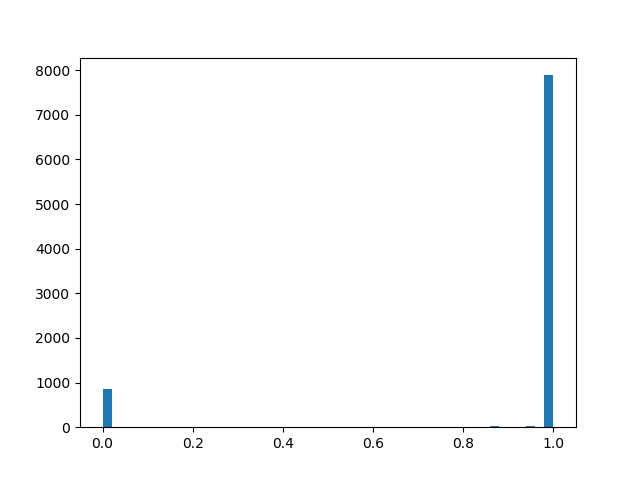
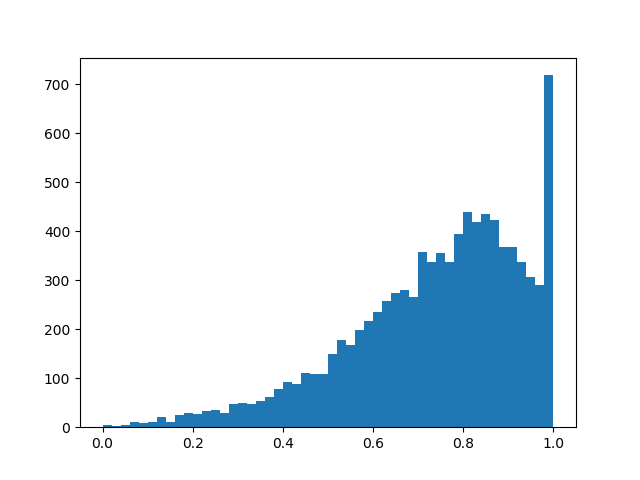
Im Wesentlichen haben wir eine „intelligente“ Dropout-Ebene, die lernt, welche Schlussfolgerungen häufiger weggeworfen werden sollten. Aber was genau optimieren wir? Bei Verlust sollten Sie das Integral der Verteilungsdichte in einen Bereich ungleich Null setzen (die Wahrscheinlichkeit, dass sich die Maske während des Trainings als ungleich Null herausstellt, einfach ausgedrückt):

Die folgenden Funktionen werden dem Push-Pull-Training, der regelmäßigen Regularisierung und anderen Implementierungsdetails hinzugefügt, die im Kapitel zur L1-Regularisierung erwähnt werden:

• Noch einmal: Unsere „intelligente“ Dropout-Ebene setzt mit einer merklichen Wahrscheinlichkeit die Ausgabe zurück, mit einigen - lässt sie so wie sie ist, und außerdem gibt es eine kleine Chance, abhängig davon $$$\ beta, \ xi, \ gamma$dass der Ausgang mit einer Zufallszahl von 0 bis 1 multipliziert wird. Der letzte Teil ist eher parasitär als nützlich für unser Endziel, aber ohne ihn in irgendeiner Weise - er wird für die Rückausbreitung eines Passbacks benötigt.
• Im Allgemeinen und $$$\ alpha$und $$$\ beta$- Trainingsparameter, aber in meinen Experimenten hatte ich das Gefühl, wenn Sie nur ein wenig fragen $$$\ beta$(0.05) und im Lernprozess ist es immer noch linear reduziert, der Algorithmus konvergiert besser als wenn Sie es ehrlich lernen. $$$\ alpha$Es ist besser, groß genug zu setzen $$$\ log {\ alpha} \ ca. 2,5$so dass anfangs Neuronen häufiger erhalten als verworfen werden, aber nicht groß genug sind, um das Sigmoid im Verlust zu sättigen.
• Wenn in Formeln ersetzt $$$\ log {\ alpha}$auf nur $$$\ alpha$als ob das Netzwerk besser konvergieren würde und weniger wahrscheinlich während des Trainings auf NaN stoßen würde. Bei diesem Manöver darf nicht vergessen werden, den Term in der Verlustfunktion und Initialisierung zu ändern.
• Auch wenn Sie betrügen und das übliche Sigmoid in Loss'e durch ein starres mit Einschränkungen ersetzen $$$\ log {\ alpha} \ in [-4, 4]$Regularisierung wird besser konvergieren und stärker wirken.
• Zu $$$\ alpha$und $$$\ beta$Sie können zusätzlich eine Regularisierung anwenden, um die Spärlichkeit weiter zu erhöhen.
• Nach dem Training sollten Sie die Ergebnisse binärisieren und das Netzwerk mit der bestimmten Maske dauerhaft trainieren, bis die Val-Genauigkeit die Konstante erreicht. Der Artikel bietet eine genauere Formel, mit der die Ausgabe eines Neurons während der Validierung oder für die Freigabe eines Netzwerks zur Freigabe deterministisch gemacht werden kann, aber es scheint, dass bis zum Ende des Trainings $$$\ alpha$Es stellt sich heraus, dass es so polarisiert ist, dass eine einfache Heuristik funktioniert: $$$\ alpha <0$- Maske 0, $$$\ alpha \ geq 0$- Maske 1 (aber das ist nicht genau). Nachdem Sie zu deterministischen Masken übergegangen sind, werden Sie einen Qualitätssprung feststellen. Vergessen Sie nicht, dass wir hier zu Nullgewichten gekommen sind und dass Sie unterhalb eines bestimmten Gewichtsschwellenwerts immer noch Maskierungsgewichte durch Nullen ersetzen müssen.
• Ein zusätzliches Plus des L0-Ansatzes: Maskierungsebenen wirken wie ein Dropout, was dem Netzwerk einen starken Regularisierungseffekt verleiht. Aber das ist ein zweischneidiges Schwert: Wenn Sie mit zu wenig trainieren $$$\ alpha$Es besteht die Gefahr, dass die vorab trainierte Netzwerkstruktur zerstört wird.

Die Experimente

Nehmen wir für das Experiment den CIFAR-10-Datensatz und ein relativ einfaches Netzwerk aus vier Faltungsschichten, gefolgt von zwei vollständig verbundenen: Conv2D, Maske, Conv2D, Maske, Pool2D, Conv2D, Maske, Conv2D, Maske, Pool2D, Abflachen, Dropout (p = 0,5) , Dicht, Maske, Dicht (logits). Es wird angenommen, dass die Algorithmen von Pruning in dickeren Netzwerken besser funktionieren, aber hier bin ich auf ein rein technisches Problem gestoßen, bei dem es an Rechenleistung mangelt. Als Optimierer wurde Adam mit einer Lernrate von 0,0015 und einer Chargengröße von 32 verwendet. Zusätzlich wurden die üblichen Regularisierungen L1 (0,00005) und L2 (0,00025) verwendet. Bildvergrößerung wurde nicht angewendet. Das Netzwerk wurde 200 Epochen vor der Konvergenz trainiert, danach wurde es beibehalten und es wurden Algorithmen zur Neuronenreduktion angewendet.

Zusätzlich zur Anwendung der oben beschriebenen Algorithmen zum Beschneiden setzen wir einen trivialen Referenzpunkt, um sicherzustellen, dass die Algorithmen überhaupt etwas bewirken. Versuchen wir, die erste jeder Schicht wegzuwerfen $$$k$Neuronen und beenden Sie das resultierende Netzwerk.

Die Grafik zeigt die Ergebnisse des Vergleichs der L1- und L0-Kanalreduktionsalgorithmen nach einer Reihe von Experimenten mit verschiedenen Regularisierungsleistungskonstanten. Die x-Achse repräsentiert die prozentuale Verringerung der Anzahl der Gewichte nach Anwendung des Algorithmus. Auf der Y-Achse die Genauigkeit des Schnittnetzwerks in der Validierungsprobe. Der blaue Balken in der Mitte gibt die ungefähre Qualität eines Netzwerks an, das noch nicht aus Neuronen herausgeschnitten wurde. Die grüne Linie repräsentiert einen einfachen L1-Maskenlernalgorithmus. Die rote Linie ist L0-beschneiden. Lila Linie - erste Entfernung $$$k$Kanäle. Schwarze Dreiecke - Training eines Netzwerks, das anfangs weniger Gewichte hatte.

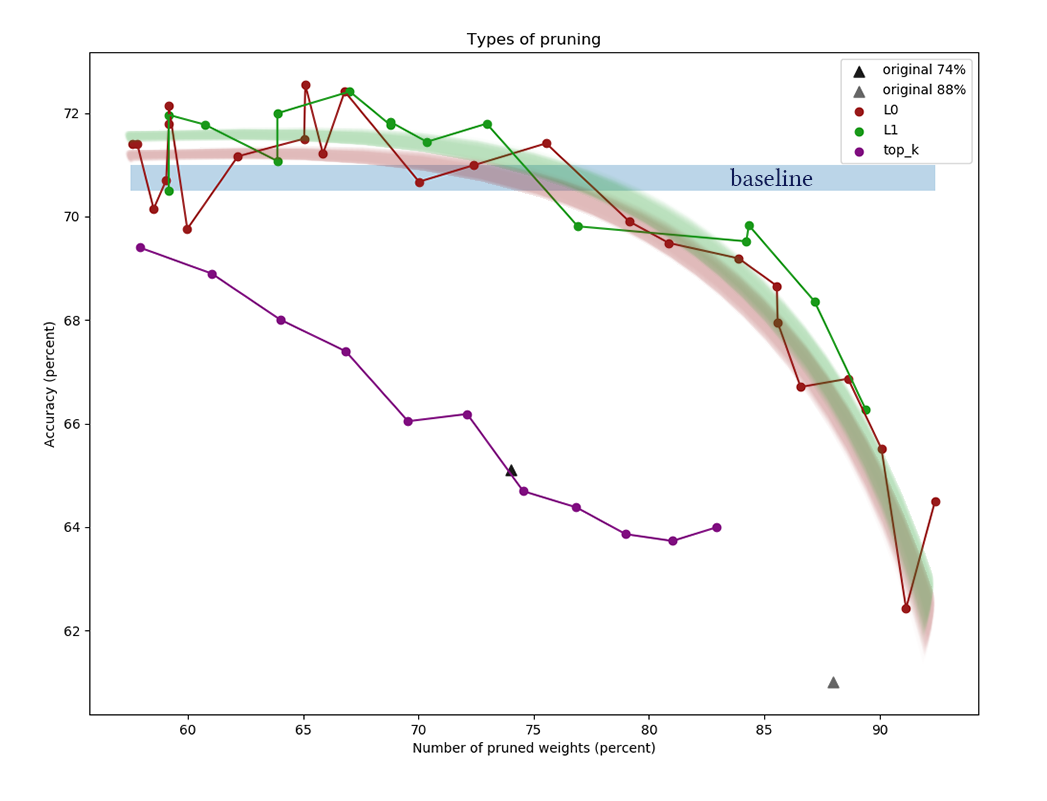
Ein weiteres Beispiel für den CIFAR-100 und ein etwas längeres und breiteres Netzwerk mit ungefähr derselben Architektur und ähnlichen Trainingsparametern:

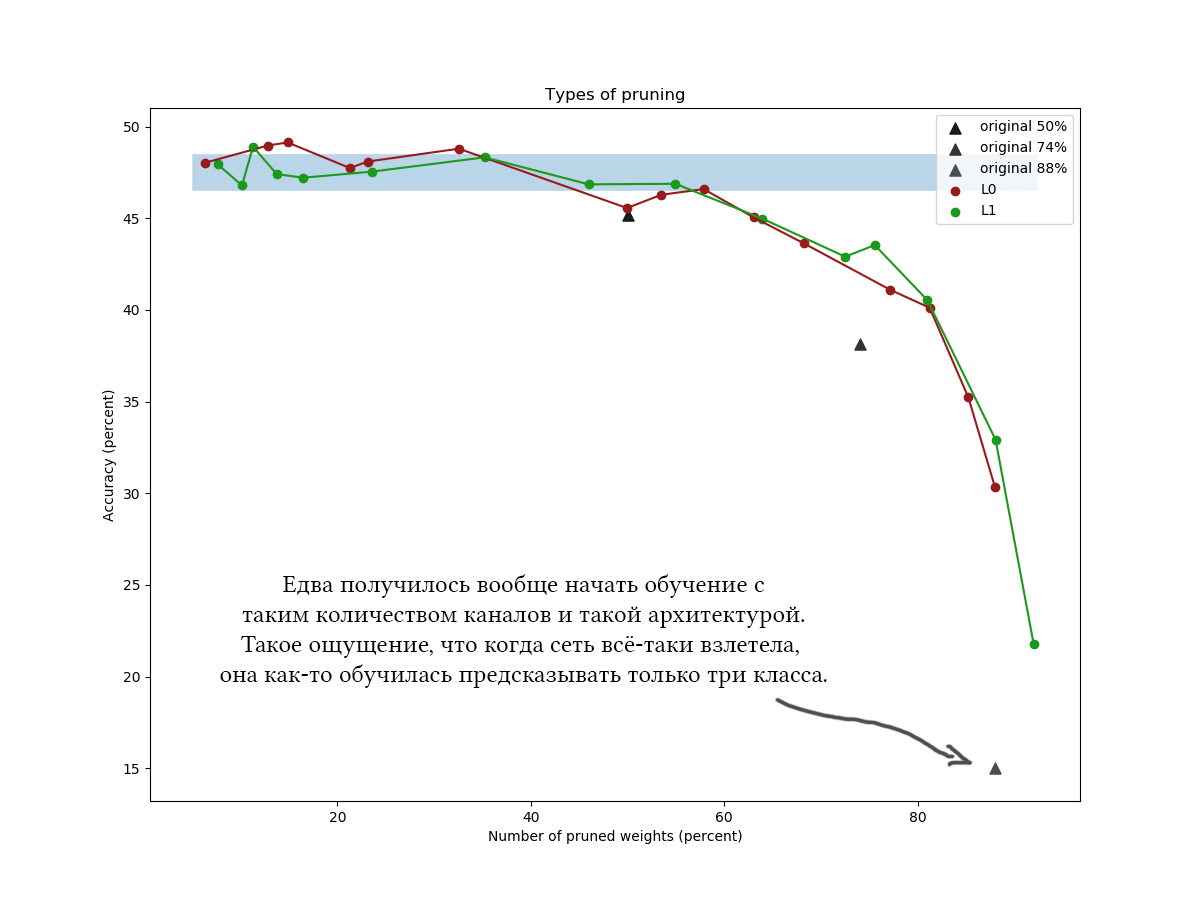
In den Diagrammen ist deutlich zu erkennen, dass ein einfacher L1-Algorithmus nicht schlechter als eine raffinierte Variationsoptimierung zurechtkommt, und es scheint, dass er die Qualität des Netzwerks bei niedrigen Komprimierungswerten sogar ein wenig mehr verbessert. Die Ergebnisse werden auch durch einmalige Experimente mit anderen Datensätzen und Netzwerkarchitekturen bestätigt. Dies ist ein absolut erwartetes Ergebnis, auf das ich mich verlassen habe, als ich Experimente zur Netzwerkreduzierung gestartet habe. Ehrlich gesagt. Seufz.

Um ehrlich zu sein, war ich ein wenig überrascht und habe versucht, mit dem Algorithmus und dem Netzwerk zu spielen: verschiedene Architekturen, Netzwerkhyperparameter, genaue Formeln, harte Betonverteilung, Anfangswerte $$$\ alpha$und $$$\ beta$, die Anzahl der Epochen der Zwischenstimmung. Die L0-Regularisierung sieht theoretisch cool aus, aber in der Praxis ist es schwieriger, Hyperparameter zu erfassen, und es dauert länger. Daher würde ich die Verwendung ohne zusätzliche Experimente und Dateiverarbeitung nicht empfehlen. Bitte berücksichtigen Sie nicht die Zeit, die Sie mit dem Lesen des Artikels verbracht haben: Das Beschneiden von L0 sieht wirklich sehr glaubwürdig aus, und ich würde sagen, dass ich den Algorithmus eher falsch angewendet habe, dass ich den versprochenen Gewinn nicht erhalten habe. Darüber hinaus ist die Variationsoptimierung die Grundlage für noch fortschrittlichere Reduktionsalgorithmen [z. B. Komprimieren neuronaler Netze mithilfe der Variation
Information Bottleneck, 2018].

:

1. . 30-50% . «» , . [The Lottery Ticket Hypothesis: Training Pruned Neural Networks, J. Frankle and M. Carbin, 2018] ( , , , ).
2. , . . , ?
3. , . 60-90% . $$$k$<7%, .
4. , (<60%) : , !
5. L1 L0 (APoZ), , .. , $$$k$.
6. , . , , , , . , , . pruning' , . - , .

, , « »? , . Tensorflow , , . , , , , , . , , . , , , .

Wahrscheinlich müssen Sie zum bequemen Maskieren Ihre eigenen Ebenen erstellen. Es ist einfach, aber achten Sie darauf, welchen Sammlungen Sie Maskierungsoptionen hinzufügen. Es ist leicht, einen Fehler zu machen und versehentlich die Parameter für die Kanalreduzierung zusammen mit allen anderen Skalen zu trainieren.

, . - , ( )*()*() , . ; , «» , . maxpool' .

, - CIFAR-10 CIFAR-100, . !