Einführung

Diese kurze Notiz wird darüber sprechen, wie das Modell der atmosphärischen Lichtstreuung in unserem letzten 4k int Appear von Jetlag strukturiert ist, dessen Partyversion auf der Demo-Party Revision 2018 im April dieses Jahres einen ehrenvollen 12. Platz im 4k Intro Compo belegte.

Sie können die Binärdatei hier kostenlos ohne SMS herunterladen.

Wenn Sie jedoch kein Windows haben oder wenn Sie keine leistungsstarke moderne Grafikkarte haben, gibt es einen beruhigenden Narren:

Die Musik für dieses Werk wurde von scharf mit 4klang geschrieben . Der gesamte Code und die Grafik blieben hinter mir.

Hier werden wir nur über das Modell der Lichtstreuung sprechen. Andere Dinge wie Werkzeuge, ein Modell einer Stadt, ein Modell der Beleuchtung und der Materialien sind nicht betroffen. Ich kann die Mutigen schicken, um die Quelle zu lesen , oder mir die Aufzeichnungen ansehen, wie ich stundenlang ertrunken bin - der größte Teil der Entwicklung wurde auf Video gemacht.

Eine langweilige Geschichte, die man verpassen sollte

Die Arbeit an dieser Arbeit begann mit der Erkenntnis, dass der Haupt-Vollzeitjob keine Zeit für die Arbeit an einem vollwertigen 4-km-Job lässt - es ist bereits fast Mitte März im Innenhof, ein paar Wochen verbleiben bis Revizen.
Es bleibt nur etwas zu finden, das einfach genug ist, um schnell, für ein paar Abende einen Compo-Füller zu bekommen. Ein weiterer dummer Rückmarsch bedeutet nicht, den Betrachter zu respektieren. Deshalb erinnerte ich mich, dass ich vor einigen Jahren einen Shader mit Streuung machen musste, und er war recht einfach, kompakt und gleichzeitig zulässig schön, wenn auch eher langsam.

Im Verlauf einer kurzen Diskussion bestand ich auf mir selbst und wir beschlossen, uns auf Folgendes zu konzentrieren: eine mit diffusem Licht gefüllte Landschaft mit Sonnenuntergang, Wolken und Dämmerungsstrahlen zu schaffen (TIL als Ausdruck "Gottstrahlen" wird übersetzt). Um die Anzahl der Schritte in der Atmosphäre nicht auf völlig nicht interaktive Werte anzuheben, müssen Sie stark rasseln (wie bei einer Monte-Carlo-Hofmethode), was zu sichtbarem Rauschen führt. Es spielt jedoch keine Rolle, ob Sie die Kamera bewegen und die Szene langsam ändern und die Umgebungsspur starten. Sie können benachbarte Bilder schmerzlos mischen und dieses Rauschen vorübergehend glätten.

Keen schrieb die Musik ziemlich schnell - sie war zwei Wochen vor der Revision fast fertig. Ich war jedoch ernsthaft von der Grippe verkrüppelt - mit einem Krankenwagen und einer Infektionskrankheit - und begann praktisch erst mit der Arbeit am Shader, als ich in einem mehr oder weniger lebenden Zustand in ein Flugzeug nach Frankfurt stieg. Der Prototyp dieses Streumodells wurde bereits in die Luft geschrieben.

Wir haben die Party-Version des Intra aus Sand und Speichel auf der Party selbst für die wenigen verbleibenden Stunden vor Ablauf der Frist (und wahrscheinlich ein paar nach; D) ausgepeitscht, während ich mich gleichzeitig von der Grippe, Schlafmangel, stundenlangen Flügen und Er war ständig abgelenkt von der Teilnahme am Shader Showdown Livecoding Compo .

Die auf der großen Leinwand gezeigte Version enthielt viele Artefakte und nur die rudimentäre Geometrie der Stadt, basierend auf dem Voronoi-Diagramm mit zufälligen Höhen.

Im Allgemeinen ist der 12. Platz recht großzügig.

Die oben gezeigte endgültige Version wurde später und in einem entspannteren Modus erstellt, einen Monat lang 1-2 Uhr pro Woche. Insgesamt dauerte die Arbeit etwa 40-50 Stunden.

Streumodell

(Hinweis: Ich programmiere Grafik nicht professionell. Dies ist mein kleines gemütliches Hobby zum Guten, wenn ein oder zwei davon sehr defokussiert sind Bier Weinstunden pro Jahr. Daher besteht keine Nullwahrscheinlichkeit, dass einige Dinge unten beschrieben und / oder falsch benannt werden. Onkel, schlag!)

Das Streumodell stammt aus dem Artikel "Hochleistungs- Außenlichtstreuung mit epipolarer Abtastung" von Egor Yusov , veröffentlicht im Buch GPU Pro 5 , mit vollständig ausgeworfener epipolarer Abtastung.

Physikalisches Modell

Sonnenphotonen bombardieren die Erdatmosphäre und interagieren mit Luftpartikeln. Ein Photon kann von einem Teilchen gestreut werden, was eine Änderung der Richtung des Photons zur Folge hat, oder es kann absorbiert werden, was bedeutet, dass das Photon verloren geht und seine Energie in eine andere Form umgewandelt wurde.
Beide Prozesse sind probabilistisch und hängen insbesondere von der Teilchendichte und der Photonenenergie ab (die ihrer Farbe entspricht).

An den Fingern haben „rote“ Photonen eine geringere Wahrscheinlichkeit, mit Luft zu interagieren, so dass sie die Dicke der Atmosphäre relativ intakt überwinden.
Blaue haben jedoch eine höhere Wahrscheinlichkeit der Streuung, weshalb sie wiederholt die Richtung ändern und beträchtliche Entfernungen in der Atmosphäre zurücklegen können, bevor sie den Betrachter erreichen (oder nicht).

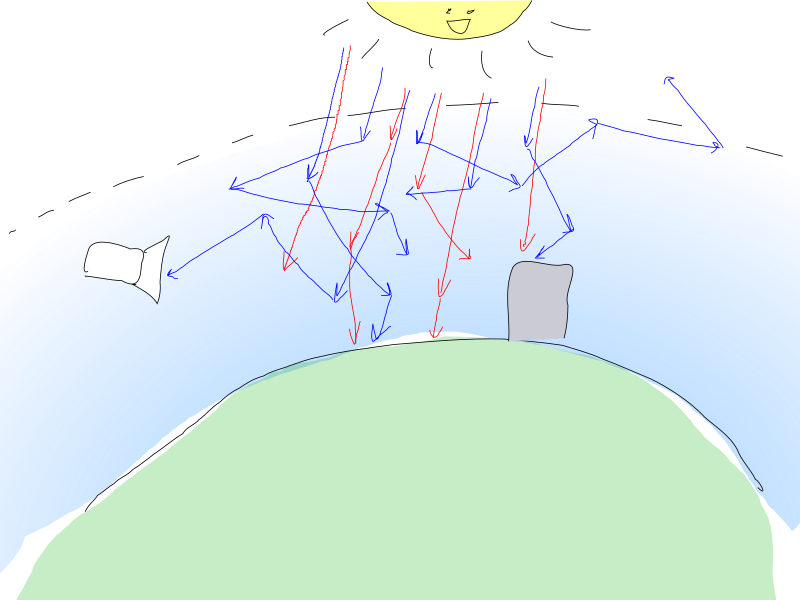
Die Parameter der Wechselwirkung von Licht mit Luft, die uns interessieren, sind wie folgt:

• $$$\ beta ^ s (x)$ - Anteil des gestreuten Lichts pro Längeneinheit an einem Punkt $$$x$
• $$$\ beta ^ a (x)$ - Anteil des absorbierten Lichts pro Längeneinheit an einem Punkt $$$x$
• $$$\ beta ^ e (x) = \ beta ^ s (x) + \ beta ^ a (x)$ - Gesamtanteil des verlorenen Lichts pro Längeneinheit an einem Punkt $$$x$
• $$$p (\ alpha)$ Ist die Winkelverteilung des gestreuten Lichts, wo $$$\ alpha$ Dies ist der Winkel zwischen dem einfallenden und dem gestreuten Strahl

Es wird angenommen, dass Luft aus zwei Arten von Partikeln besteht, deren Streuung unabhängig voneinander auftritt: Moleküle (Rayleigh-Modell) und Aerosole (relativ große kugelförmige Partikel, Mie-Streuung in der englischsprachigen Literatur). Modelle unterscheiden sich nur in unterschiedlichen Werten für die obigen Parameter.

Für beide Modelle wird angenommen, dass die Dichte der entsprechenden Partikel mit der Höhe exponentiell abnimmt: $$$\ rho = \ rho_0e ^ {- \ frac {h} {H}}$ wo $$$\ rho_0$ - Dichte auf Meereshöhe. Chancen $$$\ beta$ proportional $$$\ rho$ und ihre Bedeutungen unten sind für den Meeresspiegel angegeben.

Rayleigh-Modell

• $$$p_R (\ alpha) = \ frac {3} {16 \ pi} (1+ \ cos ^ 2 (\ alpha))$ [Nishita et al. 93, Preetham et al. 99]
• $$$\ beta_R ^ a = 0$
• $$$\ mathbf {\ beta_R ^ e} = \ mathbf {\ beta_R ^ s} = (5.8, 13.5, 33.1) _ {rgb} 10 ^ {- 6} m ^ {- 1}$ [Riley et al. 04, Bruneton und Neyret 08]
• $$$H_R = 7994 Mio.$ [Nishita et al. 93]

Aerosole

• $$$p_M (\ alpha) = \ frac {1} {4 \ pi} \ frac {3 (1-g ^ 2)} {2 (2 + g ^ 2)} \ frac {1+ \ cos ^ 2 (\ alpha)} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}}$ [Nisita et al. 93, Riley et al. 04] wo $$$g = 0,76$ [Bruneton und Neyret 08]
• $$$\ beta_M ^ s = 2 \ cdot10 ^ {- 5} m ^ {- 1}$ [Bruneton und Neyret 08]
• $$$\ beta_M ^ e = 1.1 \ beta_M ^ s$
• $$$H_M = 1200 m$ [Nishita et al. 93]

Einzelstreuungsnäherung

Die Streunäherung basiert auf der Emission eines Strahls von jedem Pixel der Kamera und der Berechnung, wie viel Licht aus der Atmosphäre aus dieser Richtung kommen soll. Jeder Strahl entspricht allen drei RGB-Lichtkomponenten, als ob drei Photonen mit entsprechenden Energien entlang dieses Strahls fliegen.

Das Licht, das die Kammer erreicht, wird durch die folgenden Prozesse in der Luft gebildet:

• Streuung (bis Feigen lernen, wie man Streuung übersetzt). Das von der Sonne emittierte Licht wird hinzugefügt, das wahrscheinlich um einen Winkel gestreut wird, der der Richtung zur Kamera entspricht.
• Absorption . Licht, das bereits entlang des Strahls fliegt, wird von der Luft absorbiert.
• Streuung . Licht, das bereits entlang des Strahls fliegt, geht durch Streuung in andere Richtungen verloren.

Aus Leistungsgründen glauben wir, dass Licht nur einmal in die Richtung der Kamera gelangen kann, wenn es einmal gestreut wird, und dass jedes andere Licht (das mehr als einmal gestreut wurde) vernachlässigt werden kann. Dies wird nicht für die Dämmerung empfohlen, aber was zu tun ist.

Dieser Ansatz ist im folgenden schönen Bild dargestellt (ich habe es versucht!):

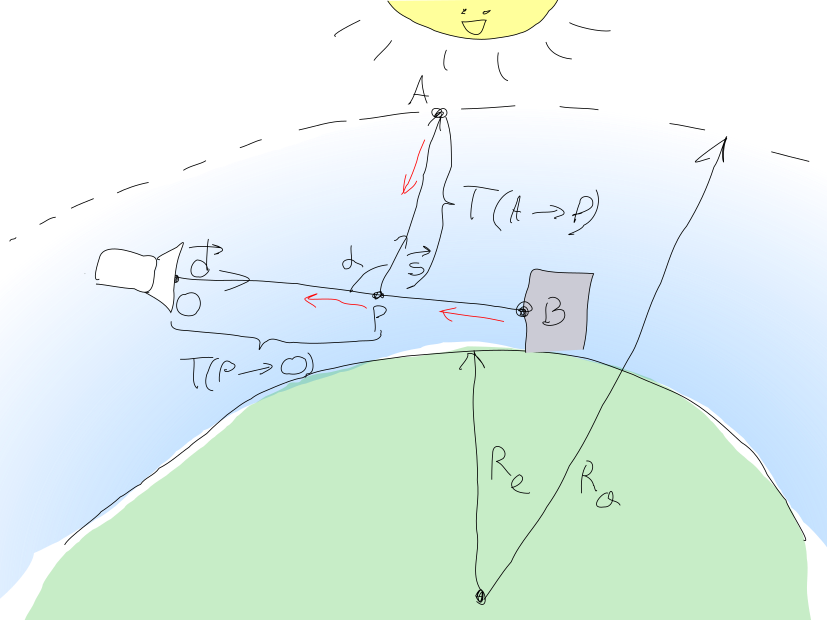
Somit ist die Lichtmenge, die von dem Kamerapixel bei erfasst werden muss $$$O$ kann als Summe berechnet werden $$$\ mathbf {L} = \ mathbf {L_ {in}} + \ mathbf {L_ {BO}}$ wo $$$\ mathbf {L_ {in}}$ - diffuses Sonnenlicht und $$$\ mathbf {L_ {BO}}$ - die Lichtmenge vom Punkt $$$B$ Objektgeometrie Szene erreichen $$$O$ .

Lichtgeometrie

$$$\ mathbf {L_ {BO}} = \ mathbf {L_O} e ^ {- \ mathbf {T} (B \ rightarrow O)}$ wo $$$\ mathbf {L_O}$ Wird das Licht von einem Punkt ausgestrahlt? $$$B$ in Richtung der Kamera.

$$$\ mathbf {T} (B \ rightarrow O)$ die optische Dicke des Mediums zwischen den Punkten genannt $$$B$ und $$$O$ und wird wie folgt berechnet:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ int_B ^ O (\ beta_M ^ e (s) + \ mathbf {\ beta_R ^ e} (s)) ds$$

Während die Mitglieder $$$\ beta$ bestehen aus konstantem Meeresspiegel und variabler Dichte, dieser Ausdruck kann umgewandelt werden in:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ beta_M ^ e \ cdot \ int_B ^ O \ rho_M (s) ds + \ mathbf {\ beta_R ^ e} \ int_B ^ O \ rho_R (s) ds = \ bar {\ mathbf {\ beta}} \ cdot \ bar {T_ \ rho} (B \ rightarrow O)$$

Bitte beachten Sie, dass ich nicht ausdrücklich offenlege $$$\ rho$ , weil wir sie später beim Hinzufügen von Wolken ändern werden. Ich mache auch darauf aufmerksam, dass $$$\ beta$ - RGB-Vektoren (mindestens $$$\ mathbf {\ beta_R}$ haben unterschiedliche Bedeutungen für die RGB-Komponenten und $$$\ beta_M$ - Vektor nur aus Gründen der Konsistenz). Mitglieder mit $$$\ rho$ Unter dem Integral befinden sich Skalare.

Sonnenlicht

Sonnenlicht $$$\ mathbf {L_ {in}}$ berechnet durch Integration über alle Punkte $$$P$ entlang des Segments $$$Ob$ und die Ansammlung von allem einfallenden Sonnenlicht, das zur Kamera streut und in der Dicke stirbt $$$\ mathbf {T} (P \ rightarrow O)$ .

Die Menge an Sonnenlicht, die einen Punkt erreicht $$$P$ wird nach einer ähnlichen Formel berechnet $$$\ mathbf {L_P} = \ mathbf {L_ {sun}} e ^ {- T (A \ rightarrow P)}$ wo $$$\ mathbf {L_ {sun}}$ - die Helligkeit der Sonne und $$$A$ Ist der Punkt, an dem der Strahl vom Punkt kommt $$$P$ der Sonne entgegen $$$\ vec {s}$ verlässt die Atmosphäre. Der Anteil dieses Lichts, der zur Kamera gestreut wird, beträgt $$$\ mathbf {L_P} \ cdot (\ mathbf {\ beta_R ^ s} (s) p_R (\ alpha) + \ beta_M ^ s (s) p_M (\ alpha))$ .

Insgesamt erhalten wir:

$$

$$\ mathbf {L_ {in}} = \ int_B ^ O \ mathbf {L_P} (s) \ cdot (\ beta_M ^ s (s) p_M (\ alpha) + \ mathbf {\ beta_R ^ s} (s) p_R (\ alpha)) \ cdot e ^ {- \ mathbf {T} (P (s) \ rightarrow O)} ds$$

Sie können feststellen, dass:

• $$$\ alpha$ ist eine Konstante für jeden Pixelstrahl der Kamera (wir glauben, dass die Sonne unendlich weit ist und die Strahlen von ihr parallel sind)
• Chancen $$$\ beta$ bestehen sowohl aus Meeresspiegelkonstanten als auch aus Dichtefunktionen $$$\ rho (s)$
• Funktionen $$$p (\ alpha)$ haben gemeinsame Faktoren für beide Streuprozesse

Auf diese Weise können Sie den Ausdruck in Folgendes konvertieren:

$$

$$\ mathbf {L_ {in}} = \ mathbf {L_ {sun}} (1+ \ cos ^ 2 (\ alpha)) (\ frac {\ frac {1} {4 \ pi} \ frac {3 (1) -g ^ 2)} {2 (2 + g ^ 2)}} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}} \ beta_M ^ s \ cdot \ mathbf {I_M} + \ frac {3} {16 \ pi} \ mathbf {\ beta_R ^ s} \ cdot \ mathbf {I_R})$$

wo

$$

$$\ mathbf {I_M} = \ int_B ^ O \ rho_M (s) e ^ {- \ mathbf {T} (A \ rechtspfeil P (s)) - \ mathbf {T} (P (s) \ rechtspfeil O)} ds$$

$$

$$\ mathbf {I_R} = \ int_B ^ O \ rho_R (s) e ^ {- \ mathbf {T} (A \ rechtspfeil P (s)) - \ mathbf {T} (P (s) \ rechtspfeil O)} ds$$

$$$I_m$ und $$$I_R$ unterscheiden sich nur in Dichtefunktionen, ihre Exponentiale sind gleich.

Niemand konnte diese Integrale analytisch berechnen, daher müssen sie mithilfe von Re-Mapping numerisch berechnet werden (wie in den Originalveröffentlichungen angegeben, ist dies nicht möglich!).

Numerische Integration

Aus Gründen der Größe und Faulheit nehmen wir so dumm wie möglich an: $$$\ int_A ^ Bf (x) dx \ approx \ frac {\ left | B - A \ right |} {N} \ sum_ {i = 0} ^ Nf (A + i \ cdot \ frac {\ vec { B - A}} {N})$

Der Strahlmarsch wird in der dem Lichtstrom entgegengesetzten Richtung durchgeführt: vom Kamerapunkt aus $$$O$ vor dem Schnittpunkt des Balkens mit der Geometrie $$$B$ . Liniensegment $$$O \ rightarrow B$ geteilt durch $$$N$ Schritte.

Initialisieren Sie vor Beginn des Marsches die Variablen:

• vec2 (zwei separate Komponenten für Rayleigh- und Aerosolstreuung) insgesamt akkumulierte optische Dicke $$$\ mathbf {T_ \ rho} (P (s) \ rightarrow O)$
• vec3 (RGB) $$$\ mathbf {I_M}$ , $$$\ mathbf {I_R}$

Weiter zum Punkt $$$P_i$ jeder Schritt dazwischen $$$O$ und $$$B$ ::

1. Lass uns strahlen $$$\ vec {s}$ in Richtung der Sonne und einen Punkt bekommen $$$A_i$ der Austritt dieses Strahls aus der Atmosphäre.
2. Berechnen Sie die Dicke $$$\ mathbf {T} (A \ rightarrow P_i)$ durch erste Berechnung $$$\ int_A ^ {P_i} \ rho_M (s) ds$ und $$$\ int_A ^ {P_i} \ rho_R (s) ds$ Verwenden Sie dieselbe Neumarschierung (mit der Anzahl der Schritte M ) und multiplizieren Sie dann die resultierenden Terme mit den entsprechenden Konstanten $$$\ beta_M ^ e$ und $$$\ mathbf {\ beta_R ^ e}$ .
3. Berechnen Sie die Dicke $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O) = \ mathbf {T_ \ rho} (P_ {i-1} \ rightarrow O) + \ rho_i (s) \ cdot ds$
4. Akkumulieren $$$\ mathbf {I_R}$ und $$$\ mathbf {I_M}$ mit diesen Werten

Die endgültige Farbe nach dem Reimarching wird aus der Summe der Begriffe berechnet:

1. Laufzeit $$$\ mathbf {L_ {BO}}$ trivial werden: eine Variable, die enthält $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O)$ enthält Wert $$$\ mathbf {T_ \ rho} (B \ rightarrow O)$ seit $$$P_i$ erreicht hat $$$B$ .
2. Durch Multiplikation $$$\ mathbf {I_R}$ und $$$\ mathbf {I_M}$ zu den entsprechenden Konstanten und durch Addition wird das Ergebnis berechnet $$$\ mathbf {L_ {in}}$

Shader

Einfache Streuung ohne jemanden

Leicht gekämmte und auskommentierte Streuquellen (fast) direkt aus dem Intra selbst entnommen:

 const float R0 = 6360e3; //    const float Ra = 6380e3; //     const vec3 bR = vec3(58e-7, 135e-7, 331e-7); //    const vec3 bMs = vec3(2e-5); //    const vec3 bMe = bMs * 1.1; const float I = 10.; //   const vec3 C = vec3(0., -R0, 0.); //   ,  (0, 0, 0)    //   //  vec2(rho_rayleigh, rho_mie) vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); //    return vec2(exp(-h/8e3), exp(-h/12e2)); } //    ,        float escape(vec3 p, vec3 d, float R) { vec3 v = p - C; float b = dot(v, d); float det = b * b - dot(v, v) + R*R; if (det < 0.) return -1.; det = sqrt(det); float t1 = -b - det, t2 = -b + det; return (t1 >= 0.) ? t1 : t2; } //         `L`   `p`   `d` //   `steps`  //  vec2(depth_int_rayleigh, depth_int_mie) vec2 scatterDepthInt(vec3 o, vec3 d, float L, float steps) { vec2 depthRMs = vec2(0.); L /= steps; d *= L; for (float i = 0.; i < steps; ++i) depthRMs += densitiesRM(o + d * i); return depthRMs * L; } //   (  --   ) vec2 totalDepthRM; vec3 I_R, I_M; //    vec3 sundir; //    ,    `-d`   `L`   `o`   `d`. // `steps` --    void scatterIn(vec3 o, vec3 d, float L, float steps) { L /= steps; d *= L; //   O  B for (float i = 0.; i < steps; ++i) { // P_i vec3 p = o + d * i; vec2 dRM = densitiesRM(p) * L; //  T(P_i -> O) totalDepthRM += dRM; //     T(P_i ->O) + T(A -> P_i) // scatterDepthInt()    T(A -> P_i) vec2 depthRMsum = totalDepthRM + scatterDepthInt(p, sundir, escape(p, sundir, Ra), 4.); vec3 A = exp(-bR * depthRMsum.x - bMe * depthRMsum.y); I_R += A * dRM.x; I_M += A * dRM.y; } } //    // O = o --   // B = o + d * L --   // Lo --     B vec3 scatter(vec3 o, vec3 d, float L, vec3 Lo) { totalDepthRM = vec2(0.); I_R = I_M = vec3(0.); //  T(P -> O) and I_M and I_R scatterIn(o, d, L, 16.); // mu = cos(alpha) float mu = dot(d, sundir); //     return Lo * exp(-bR * totalDepthRM.x - bMe * totalDepthRM.y) //   + I * (1. + mu * mu) * ( I_R * bR * .0597 + I_M * bMs * .0196 / pow(1.58 - 1.52 * mu, 1.5)); } 

Halt den Shader an

Die Wolken

Nicht schlecht, aber ein solches Bild könnte auch mit einem listigen Stapel von Verläufen viel einfacher erhalten werden.

Auf trügerische Weise ist es viel schwieriger, Wolken und Gottesstrahlen zu bekommen. Fügen wir hinzu.

Die Idee ist, die Wolken mit Aerosolen zu approximieren und nur die DichtefunktionsdichtenRM densitiesRM() modifizieren. Dies ist möglicherweise nicht so physikalisch korrekt, wie wir es gerne hätten (ich habe keine Ahnung, wie sich die Streuung von Licht in Wolken in Computergrafiken tatsächlich nähert).

 //      const float low = 1e3, hi = 25e2; // vec4 noise24(vec2 v) --       // float t --  float noise31(vec3 v) { return (noise24(v.xz).x + noise24(v.yx).y) * .5; } vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); vec2 retRM = vec2(exp(-h/8e3), exp(-h/12e2) * 8.); //    () if (low < h && h < hi) { vec3 v = 15e-4 * (p + t * vec3(-90., 0., 80.)); //    <s></s>      :     retRM.y += 250. * step(vz, 38.) * smoothstep(low, low + 1e2, h) * smoothstep(hi, hi - 1e3, h) * smoothstep(.5, .55, //  :   .75 * noise31(v) + .125 * noise31(v*4. + t) + .0625 * noise31(v*9.) + .0625 * noise31(v*17.)-.1 ); } return retRM; } 

Entgegen den Erwartungen bekommen wir keine schönen Wolken, einen süßen Sieg und Fans, sondern Artefakte. Der Versuch, die Anzahl der Schritte zu erhöhen, die Artefakte auf der Stirn verursachen, entfernt die Leistung nicht vollständig, beeinträchtigt sie jedoch erheblich.

Lösungen Krücken, die das Intra drücken:

• Die unangenehmsten Artefakte am Horizont verstecken sich hinter den Bergen
• Wolken werden nur in der Nähe der Kamera hinzugefügt.
• Wenn Monte-Karlovschina hinzugefügt wird, wird jeder Marschstrahl um einen zufälligen Versatz verschoben: for (float i = pixel_random.w; i < steps; ++i) . Dies summiert sich zu dem Rauschen, das Sie vorübergehend durch Mischen aufeinanderfolgender Frames ausgleichen müssen.

• Die Anzahl der Schritte für Zonen, die mehr Details erfordern, nimmt zu (z. B. eine Ebene mit Wolken). Aus diesem scatterImpl() eine solch absurde Trennung der Funktionen in scatterImpl() und scatterDepthInt() :

  
  

   //    scatterIn() vec2 depthRMsum = totalDepthRM; float l = max(0., escape(p, sundir, R0 + hi)); if (l > 0.) //   16  depthRMsum += scatterDepthInt(p, sundir, l, 16.); //     4- depthRMsum += scatterDepthInt(p + sundir * l, sundir, escape(p, sundir, Ra), 4.); 

  
  

   //   scatter() //  10    float l = 10e3; if (L < l) scatterIn(o, d, L, 16.); else { scatterIn(o, d, l, 32.); // 8  --     scatterIn(o+d*l, d, Ll, 8.); } 

  
  

Ausrichtung mit der Szenengeometrie

Infolge der herkömmlichen Neuabbildung der Abstands- und Schattenfunktionen wurden bereits der Abstand L zum Punkt B und die Pixelfarbe Lo erhalten. Diese Werte werden einfach in die scatter() Funktion eingesetzt. Wenn der Strahl nicht an der Geometrie anliegt und die Szene verlässt, ist die Farbe Lo Null und L mit escape() berechnet - es wird angenommen, dass der Strahl die Atmosphäre verlassen hat.

Wie alles.

... In der Tat natürlich nicht alle. Es ist ziemlich schmerzhaft, alle Teile aneinander zu reiben, damit es insgesamt glaubwürdig aussieht. Nur ein Haufen Aufhebens um Drehparameter, Szenengeometrie, Rauschfunktionen, Flugbahn und Kamerawinkel. Ich fürchte, ich habe hier keinen guten Rat, außer dass ich über viele Stunden iteriere und meinen Kopf gegen die Wand stoße.

Minimierung

Nach der Verarbeitung des Shader-Minifizierers ist der endgültige Shader-Scatter-Code etwa 1500 Byte groß. Crinkler komprimiert es auf ~ 700 Bytes, was ungefähr 30% des gesamten Shader-Codes entspricht.

Zucht

Ich weiß nicht, wie man Computergrafiken macht.