Polynom-Regressionsmodell

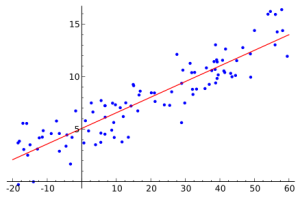
In einfachen Worten, das Regressionsmodell in der mathematischen Statistik basiert auf bekannten Daten, die Zahlenpaare sind. Die Anzahl solcher Paare ist vorbestimmt. Wenn Sie sich vorstellen, dass die erste Zahl in einem Paar der Wert der Koordinate ist $$$x$ und der zweite $$$y$ Dann kann die Menge solcher Zahlenpaare auf der Ebene im kartesischen Koordinatensystem als eine Menge von Punkten dargestellt werden. Diese Zahlenpaare werden nicht zufällig genommen. In der Praxis hängt die zweite Zahl in der Regel von der ersten ab. Eine Regression aufzubauen bedeutet, eine Linie (genauer gesagt eine Funktion) aufzunehmen, die sich so nah wie möglich vielen der oben genannten Punkte nähert (annähert).

Wofür ist das alles? Dies ist vor allem für die Vorbereitung der sogenannten notwendig Prognosen. Müssen oft herausfinden $$$y$ nur wissen $$$x$ wenn es sich von denen X unterscheidet, auf deren Grundlage die Regression aufgebaut wurde. Ich werde ein einfaches Beispiel geben. Es gibt Statistiken über die Abhängigkeit des Wachstums einer Person von ihrem Alter, basierend auf 100 verschiedenen untersuchten Personen. Wir haben also 100 Zahlenpaare {Alter; Wachstum}. Gleichzeitig ist „Wachstum“ eine abhängige Größe und „Alter“ unabhängig. Durch die korrekte Erstellung eines Regressionsmodells können wir das Wachstum mit Sicherheit anhand eines beliebigen Alterswerts „vorhersagen“.

In der Praxis werden je nach Situation lineare, parabolische, Potenz- und andere Arten von Funktionen bei der Konstruktion von Regressionsmodellen verwendet. In der mathematischen Statistik wird am häufigsten das lineare Regressionsmodell berücksichtigt. Manchmal berühren sie einen komplizierteren Fall - ein parabolisches Modell. Bei einer Verallgemeinerung ist es leicht zu erraten, dass lineare und parabolische Modelle besondere Fälle eines komplexeren Modells sind - Polynom. Ein Regressionsmodell zu erstellen bedeutet, die Parameter der Funktion zu finden, die darin angezeigt werden. Für die lineare Regression - zwei Parameter: Koeffizient und freier Term.

Die Polynomregression kann in der mathematischen Statistik verwendet werden, um die Trendkomponenten von Zeitreihen zu modellieren. Eine Zeitreihe ist in der Tat eine Reihe von Zahlen, die von der Zeit abhängen. Zum Beispiel die durchschnittliche Tagestemperatur des vergangenen Jahres oder das monatliche Einkommen des Unternehmens. Die Reihenfolge des simulierten Polynoms wird durch spezielle Methoden bewertet, beispielsweise durch das Kriterium der Reihe. Das Ziel, ein Modell der Polynomregression im Bereich der Zeitreihen zu konstruieren, ist immer noch dasselbe - Prognose.

Zunächst betrachten wir das Problem der Polynomregression allgemein. Alle Überlegungen basieren auf einer Verallgemeinerung der Überlegungen bei linearen und parabolischen Regressionsproblemen. Nach diesen Überlegungen werde ich auf einen Sonderfall eingehen - die Betrachtung dieses Modells für Zeitreihen.

Es seien zwei Beobachtungsreihen gegeben $$$x_i$ (unabhängige Variable) und $$$y_i$ (abhängige Variable) $$$i = \ overline {1, n}$ . Die Polynomgleichung hat die Form

$$

$$y = \ sum \ limit_ {j = 0} ^ k b_jx ^ j, \ \ \ \ \ (1)$$

wo $$$b_j$ - Parameter dieses Polynoms, $$$j = \ overline {0, k}$ . Unter ihnen $$$b_0$ - ein freies Mitglied. Lassen Sie uns die OLS-Parameter (Least Squares) finden $$$b_j$ gegebene Regression.

In Analogie zur linearen Regression basiert OLS auch auf der Minimierung des folgenden Ausdrucks:

$$

$$S = \ sum \ limit_ {i = 1} ^ n \ left (\ hat y_i-y_i \ right) ^ 2 \ to \ min \ \ \ \ \ (2)$$

Hier $$$\ hat y_i$ - theoretische Werte, die die Werte des Polynoms (1) an Punkten sind $$$x_i$ . Durch Einsetzen von (1) in (2) erhalten wir

$$

$$S = \ sum \ limit_ {i = 1} ^ n \ left (\ sum_ {j = 0} ^ kb_jx_i ^ j-y_i \ right) ^ 2 \ to \ min.$$

Basierend auf der notwendigen Bedingung für das Extremum der Funktion $$$(k + 1)$ Variablen $$$S = S (b_0, b_1, \ dots, b_k)$ wir setzen seine partiellen Ableitungen mit Null gleich, d.h.

$$

$$S '_ {b_p} = 2 \ Summe \ Grenzen_ {i = 1} ^ nx_i ^ p \ links (\ Summe \ Grenzen_ {j = 0} ^ kb_jx_i ^ j-y_i \ rechts) = 0, \ \ \ p = \ overline {0, k}.$$

Wenn wir die linke und rechte Seite jeder Gleichheit durch 2 teilen, erhalten wir die zweite Summe:

$$

$$\ sum \ limit_ {i = 1} ^ nx_i ^ p \ left (b_0 + b_1x_i + b_2x_i ^ 2 + \ dots + b_kx_i ^ k \ right) - \ sum \ border_ {i = 1} ^ nx_i ^ py_i = 0 , \ \ \ p = \ overline {0, k}.$$

Durch Öffnen der Klammern übertragen wir jeweils $$$p$ th Ausdruck, der letzte Begriff mit $$$y_i$ nach rechts und teilen Sie beide Seiten durch $$$n$ . Als Ergebnis haben wir $$$(k + 1)$ Ausdrücke, die ein System linearer Normalgleichungen für bilden $$$b_p$ . Es hat die folgende Form:

$$

$$\ left \ {\ begin {array} {l} b_0 + b_1 \ overline x + b_2 \ overline {x ^ 2} + \ dots + b_k \ overline {x ^ k} = \ overline y \\ b_0 \ overline x + b_1 \ overline {x ^ 2} + b_2 \ overline {x ^ 3} + \ dots + b_k \ overline {x ^ {k + 1}} = \ overline {xy} \\ b_0 \ overline {x ^ 2} + b_1 \ overline {x ^ 3} + b_2 \ overline {x ^ 4} + \ dots + b_k \ overline {x ^ {k + 2}} = \ overline {x ^ 2y} \\ \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \\ b_0 \ overline {x ^ k} + b_1 \ overline {x ^ {k + 1}} + b_2 \ overline {x ^ {k + 2}} + \ dots + b_k \ overline {x ^ {2k}} = \ overline {x ^ ky} \ end {array} \ right. \ \ \ \ \ (3)$$

Sie können das System (3) in Matrixform umschreiben: $$$AB = C$ wo

$$

$$A = \ left (\ begin {array} {ccccc} 1 & \ overline x & \ overline {x ^ 2} & \ ldots & \ overline {x ^ k} \\ \ overline x & \ overline {x ^ 2 } & \ overline {x ^ 3} & \ ldots & \ overline {x ^ {k + 1}} \\ \ overline {x ^ 2} & \ overline {x ^ 3} & \ overline {x ^ 4} & \ ldots & \ overline {x ^ {k + 2}} \\ \ vdots & \ vdots & \ vdots & \ ddots & \ vdots \\ \ overline {x ^ k} & \ overline {x ^ {k + 1} } & \ overline {x ^ {k + 2}} & \ ldots & \ overline {x ^ {2k}} \ end {array} \ right), \ \ B = \ left (\ begin {array} {c} b_0 \\ b_1 \\ b_2 \\\ vdots \\ b_k \ end {array} \ right), \ \ C = \ left (\ begin {array} {c} \ overline y \\\ overline {xy} \\ \ overline {x ^ 2y} \\\ vdots \\\ overline {x ^ ky} \ end {array} \ right).$$

Nun wenden wir uns der Anwendung der obigen Tatsachen im Fall von Zeitreihen zu. Lassen Sie Zeitreihen gegeben werden $$$x_t$ wo $$$t = \ overline {1, n}$ . Es ist erforderlich, einen Polynomordnungstrend zu erstellen $$$k$ , die die angegebenen Zeitreihen so genau wie möglich approximiert. Als unabhängige Variable $$$x$ wir werden nehmen $$$t$ basierend auf der Definition einer Zeitreihe. Diese Xs sind eine Reihe natürlicher Zahlen, die einen Zeitraum bezeichnen. Als $$$y$ Zeitreihenwerte werden genommen $$$x_t$ . Es ist ersichtlich, dass die Werte der Elemente $$$a_ {ij}$ Systemmatrizen $$$A$ unabhängig von $$$x_t$ . Da im allgemeinen Fall natürlich

$$

$$a_ {ij} = \ overline {x ^ {i + j-2}} = \ frac1n \ sum \ limit_ {r = 1} ^ nx_r ^ {i + j-2},$$

dann im Fall von Zeitreihen

$$

$$a_ {ij} = \ frac1n \ sum \ limit_ {r = 1} ^ nr ^ {i + j-2},$$

wo $$$i, j = \ overline {1, (k + 1)}.$

Gegenstände $$$c_j$ Matrixvektoren freier Terme $$$C$ allgemein erhalten als

$$

$$c_j = \ overline {x ^ {j-1} y} = \ frac1n \ sum \ limit_ {r = 1} ^ nx_r ^ {j-1} y_r.$$

Und im Fall von Zeitreihen

$$

$$c_j = \ frac1n \ sum \ limit_ {r = 1} ^ nr ^ {j-1} x_r,$$

wo $$$j = \ overline {1, (k + 1)}.$

Nachdem wir also System (3) gelöst haben, können wir die gewünschten Parameter des Polynomtrends finden $$$b_0, \ dots, b_k.$

Um die Matrizen des Systems auszufüllen und zu lösen, kann eine der numerischen Methoden verwendet werden, um einen Trend auf einem Computer zu modellieren. In diesem Fall ist das Berechnungsergebnis ziemlich genau.

Infolgedessen hat die Trendkomponente die Form:

$$

$$T_t = \ sum \ limit_ {i = 0} ^ kb_it ^ i, \ \ \ t = 0,1,2, \ dots.$$

Es ist auch erwähnenswert, dass die simulierte Trendkomponente $$$T_t$ , nicht nur für aktuelle Perioden bestimmt $$$[1; n]$ , aber auch für zukünftige Perioden $$$t> n$ .

Ich stelle sofort fest, dass die Polynomregression nur die Trendkomponente der Zeitreihe modelliert. Ein vollständiges Zeitreihenmodell impliziert auch andere Komponenten, was den Rahmen dieses Artikels sprengt.

In der Praxis habe ich persönlich keine Zeitreihen mit einer Polynomtrendreihenfolge von mehr als 2 gesehen. Dies erklärt die Prävalenz linearer und prabolischer Regressionsmodelle als besondere Fälle von Polynomen.