Wenn Sie in einigen Sätzen beschreiben, wie das Prinzip des Sortieraustauschs funktioniert, dann:

1. Array-Elemente werden paarweise verglichen
2. Wenn das Element links ^* größer als das Element rechts ist, werden die Elemente vertauscht
3. Wiederholen Sie die Schritte 1-2, bis das Array sortiert ist

^{* - Das Element auf der linken Seite bedeutet das Element aus dem verglichenen Paar, das näher am linken Rand des Arrays liegt. Dementsprechend befindet sich das Element rechts näher am rechten Rand.}

Ich entschuldige mich sofort für die Wiederholung von bekanntem Material. Es ist unwahrscheinlich, dass mindestens einer der Algorithmen in diesem Artikel eine Offenbarung für Sie ist. Über diese Sortierungen auf Habré wurde bereits viele Male geschrieben (einschließlich mir - 1 , 2 , 3 ) und gefragt, warum noch einmal auf dieses Thema zurückgegriffen werden soll. Da ich mich jedoch entschlossen habe, eine zusammenhängende Artikelserie über alle Sortierungen auf der Welt zu schreiben, muss ich die Austauschmethoden auch in der Expressversion durchlaufen. Wenn man die folgenden Klassen betrachtet, wird es bereits viele neue (und nur wenige Leute kennen) Algorithmen geben, die separate interessante Artikel verdienen.

Traditionell umfassen "Austauscher" Sortierungen, bei denen sich Elemente zufällig (pseudo) ändern (Bogosort, Bozosort, Permsort usw.). Ich habe sie jedoch nicht in diese Klasse aufgenommen, da ihnen Vergleiche fehlen. Es wird einen separaten Artikel über diese Sortierungen geben, in dem wir viel über Wahrscheinlichkeitstheorie, Kombinatorik und thermischen Tod des Universums philosophieren.

Dumme Sortierung :: Handlanger-Sortierung

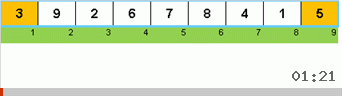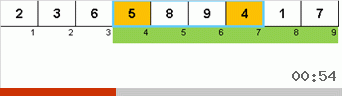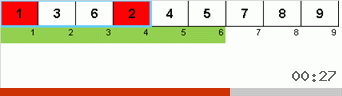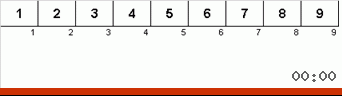
1. Vergleichen Sie die Elemente an den Enden des Subarrays (und ändern Sie sie gegebenenfalls).
2. Wir nehmen zwei Drittel des Subarrays von Anfang an und wenden den allgemeinen Algorithmus rekursiv auf diese 2/3 an.
3. Wir nehmen zwei Drittel des Subarrays von seinem Ende und wenden den allgemeinen Algorithmus rekursiv auf diese 2/3 an.
4. Und wieder nehmen wir zwei Drittel des Subarrays von Anfang an und wenden den allgemeinen Algorithmus rekursiv auf diese 2/3 an.

Ein Subarray ist zunächst ein ganzes Array. Und dann teilt die Rekursion das übergeordnete Subarray in 2/3 auf, führt Vergleiche / Austausch an den Enden der fragmentierten Segmente durch und ordnet schließlich alles an.

def stooge_rec(data, i = 0, j = None): if j is None: j = len(data) - 1 if data[j] < data[i]: data[i], data[j] = data[j], data[i] if j - i > 1: t = (j - i + 1) // 3 stooge_rec(data, i, j - t) stooge_rec(data, i + t, j) stooge_rec(data, i, j - t) return data def stooge(data): return stooge_rec(data, 0, len(data) - 1) 

Es sieht schizophren aus, ist aber dennoch zu 100% korrekt.

Träge Sortierung :: Langsame Sortierung

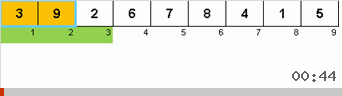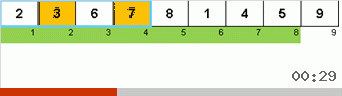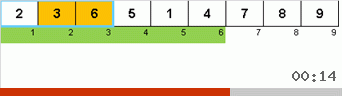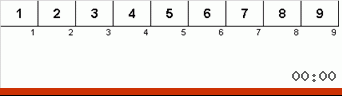
Und hier beobachten wir rekursive Mystik:

1. Wenn das Subarray aus einem Element besteht, schließen wir die Rekursion ab.
2. Wenn ein Subarray aus zwei oder mehr Elementen besteht, teilen Sie es in zwei Hälften.
3. Wir wenden den Algorithmus rekursiv auf die linke Hälfte an.
4. Wir wenden den Algorithmus rekursiv auf die rechte Hälfte an.
5. Elemente an den Enden des Subarrays werden verglichen (und bei Bedarf geändert).
6. Wir wenden den Algorithmus rekursiv auf ein Subarray ohne das letzte Element an.

Ein Subarray ist zunächst das gesamte Array. Und die Rekursion wird sich weiter halbieren, vergleichen und ändern, bis alles sortiert ist.

 def slow_rec(data, i, j): if i >= j: return data m = (i + j) // 2 slow_rec(data, i, m) slow_rec(data, m + 1, j) if data[m] > data[j]: data[m], data[j] = data[j], data[m] slow_rec(data, i, j - 1) def slow(data): return slow_rec(data, 0, len(data) - 1) 

Es sieht nach Unsinn aus, aber das Array ist geordnet.

Warum funktionieren StoogeSort und SlowSort richtig?

Ein neugieriger Leser wird eine vernünftige Frage stellen: Warum funktionieren diese beiden Algorithmen überhaupt? Sie scheinen einfach zu sein, aber es ist nicht sehr offensichtlich, dass Sie so etwas sortieren können.

Schauen wir uns zuerst Slow sort an. Der letzte Punkt dieses Algorithmus deutet darauf hin, dass die rekursiven Bemühungen der schleppenden Sortierung nur darauf abzielen, das größte Element im Subarray ganz rechts zu platzieren. Dies macht sich insbesondere dann bemerkbar, wenn Sie den Algorithmus auf ein nachgeordnetes Array anwenden:



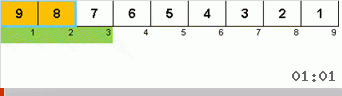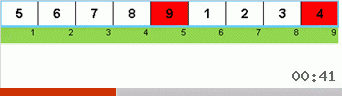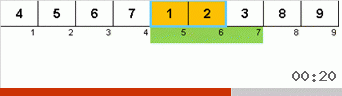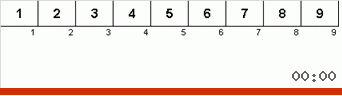
Es ist deutlich zu sehen, dass die Maxima auf allen Rekursionsebenen schnell nach rechts wandern. Dann werden diese Maxima, wo sie benötigt werden, aus dem Spiel ausgeschaltet: Der Algorithmus ruft sich selbst auf - aber ohne das letzte Element.

Bei Stooge passiert eine ähnliche Magie:



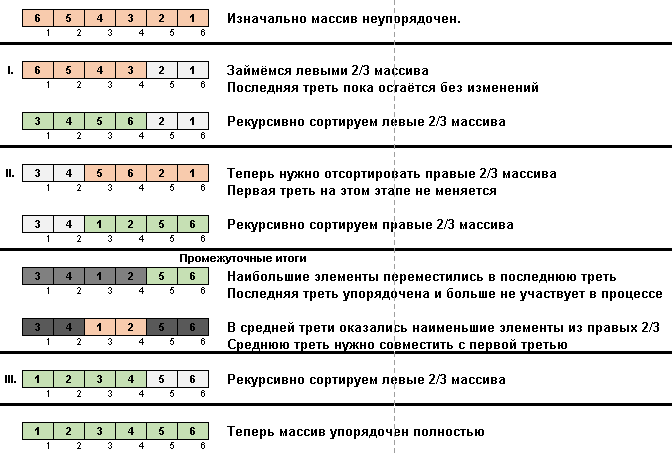
In der Tat wird der Schwerpunkt auch auf maximale Elemente gelegt. Nur die langsame Sortierung verschiebt sie nacheinander zum Ende, und die Stooge-Sortierung drückt ein Drittel der Elemente des Subarrays (das größte von ihnen) in das am weitesten rechts liegende Drittel des Zellenraums.

Wir wenden uns Algorithmen zu, bei denen bereits alles ganz offensichtlich ist.

Dumme Sortierung :: Dumme Sortierung

Sehr sorgfältige Sortierung. Es geht vom Anfang des Arrays bis zum Ende und vergleicht benachbarte Elemente. Wenn zwei benachbarte Elemente ausgetauscht werden mussten, kehrt die Sortierung für alle Fälle zum Anfang des Arrays zurück und beginnt von vorne.

 def stupid(data): i, size = 1, len(data) while i < size: if data[i - 1] > data[i]: data[i - 1], data[i] = data[i], data[i - 1] i = 1 else: i += 1 return data 

Gnome sort :: Gnome sort

Fast das Gleiche, aber das Sortieren während des Austauschs kehrt nicht zum Anfang des Arrays zurück, sondern geht nur einen Schritt zurück. Es stellt sich heraus, dass dies ausreicht, um alles zu klären.

 def gnome(data): i, size = 1, len(data) while i < size: if data[i - 1] <= data[i]: i += 1 else: data[i - 1], data[i] = data[i], data[i - 1] if i > 1: i -= 1 return data 

Optimierte Zwergsortierung

Sie können aber nicht nur beim Rückzug sparen, sondern auch beim Vorwärtsbewegen. Bei mehreren aufeinander folgenden Austauschen müssen Sie so viele Schritte zurücktreten. Und dann müssen Sie zurückgehen (indem Sie die Elemente vergleichen, die bereits relativ zueinander angeordnet sind). Wenn Sie sich an die Position erinnern, von der aus der Austausch begonnen hat, können Sie sofort zu dieser Position springen, wenn der Austausch abgeschlossen ist.

 def gnome(data): i, j, size = 1, 2, len(data) while i < size: if data[i - 1] <= data[i]: i, j = j, j + 1 else: data[i - 1], data[i] = data[i], data[i - 1] i -= 1 if i == 0: i, j = j, j + 1 return data 

Blasensortierung :: Blasensortierung

Im Gegensatz zur dummen und gnomeischen Sortierung treten beim Austausch von Elementen in der Blase keine Rückgaben auf - sie bewegt sich weiter vorwärts. Wenn Sie das Ende erreichen, wird das größte Element des Arrays bis zum Ende verschoben.

Dann wiederholt der Sortiervorgang den gesamten Vorgang erneut, wodurch sich das zweite Element im Dienstalter an vorletzter Stelle befindet. Bei der nächsten Iteration ist das drittgrößte Element das dritte vom Ende usw.

 def bubble(data): changed = True while changed: changed = False for i in range(len(data) - 1): if data[i] > data[i+1]: data[i], data[i+1] = data[i+1], data[i] changed = True return data 

Optimierte Blasensortierung

Sie können ein wenig an den Gängen am Anfang des Arrays profitieren. Dabei werden die ersten Elemente vorübergehend relativ zueinander angeordnet (dieses sortierte Teil ändert ständig seine Größe - es nimmt ab, es nimmt zu). Dies lässt sich leicht beheben und mit einer neuen Iteration können Sie einfach über eine Gruppe solcher Elemente springen.
_{(Ich werde die getestete Implementierung in Python hier etwas später hinzufügen. Ich hatte keine Zeit, sie vorzubereiten.)}

Shaker Sort :: Shaker Sort
(Cocktail-Sorte :: Cocktail-Sorte)

Eine Art Blase. Schieben Sie beim ersten Durchgang wie gewohnt das Maximum bis zum Ende. Dann drehen wir uns scharf um und schieben das Minimum an den Anfang. Die sortierten Randbereiche des Arrays werden nach jeder Iteration größer.

 def shaker(data): up = range(len(data) - 1) while True: for indices in (up, reversed(up)): swapped = False for i in indices: if data[i] > data[i+1]: data[i], data[i+1] = data[i+1], data[i] swapped = True if not swapped: return data 

Odd-Even-Sortierung :: Odd-Even-Sortierung

Wieder Iterationen über den paarweisen Vergleich benachbarter Elemente beim Bewegen von links nach rechts. Nur zuerst vergleichen wir die Paare, in denen das erste Element beim Zählen ungerade ist und das zweite gerade ist (d. H. Das erste und zweite, dritte und vierte, fünfte und sechste usw.). Und dann umgekehrt - gerade + ungerade (zweite und dritte, vierte und fünfte, sechste und siebte usw.). In diesem Fall machen viele große Elemente des Arrays bei einer Iteration gleichzeitig einen Schritt vorwärts (in der Blase erreicht das größte für die Iteration das Ende, aber der Rest der ziemlich großen Elemente bleibt fast an Ort und Stelle).

Übrigens war dies ursprünglich eine parallele Sortierung mit O (n) -Komplexität. AlgoLab muss im Abschnitt "Parallele Sortierung" implementiert werden.

 def odd_even(data): n = len(data) isSorted = 0 while isSorted == 0: isSorted = 1 temp = 0 for i in range(1, n - 1, 2): if data[i] > data[i + 1]: data[i], data[i + 1] = data[i + 1], data[i] isSorted = 0 for i in range(0, n - 1, 2): if data[i] > data[i + 1]: data[i], data[i + 1] = data[i + 1], data[i] isSorted = 0 return data 

Kammsortierung :: Kammsortierung

Die erfolgreichste Modifikation der Blase. Der Geschwindigkeitsalgorithmus konkurriert mit der schnellen Sortierung.

In allen vorherigen Variationen haben wir die Nachbarn verglichen. Dabei werden zunächst Elementpaare betrachtet, die sich in maximalem Abstand voneinander befinden. Bei jeder neuen Iteration wird dieser Abstand gleichmäßig kleiner.

 def comb(data): gap = len(data) swaps = True while gap > 1 or swaps: gap = max(1, int(gap / 1.25)) # minimum gap is 1 swaps = False for i in range(len(data) - gap): j = i + gap if data[i] > data[j]: data[i], data[j] = data[j], data[i] swaps = True return data 

Schnelle Sortierung :: Schnelle Sortierung

Nun, der fortschrittlichste Austauschalgorithmus.

1. Teilen Sie das Array in zwei Hälften. Das mittlere Element ist die Referenz.
2. Wir bewegen uns vom linken Rand des Arrays nach rechts, bis wir ein Element finden, das größer als das Referenzelement ist.
3. Wir bewegen uns vom rechten Rand des Arrays nach links, bis wir ein Element finden, das kleiner als das Referenzelement ist.
4. Wir tauschen die beiden Elemente aus den Punkten 2 und 3 aus.
5. Wir führen die Punkte 2-3-4 weiter aus, bis aufgrund der gegenseitigen Bewegung ein Treffen stattfindet.
6. Am Treffpunkt ist das Array in zwei Teile unterteilt. Für jeden Teil wenden wir rekursiv einen schnellen Sortieralgorithmus an.

Warum funktioniert es? Links vom Treffpunkt befinden sich Elemente, die kleiner oder gleich dem Referenzpunkt sind. Rechts vom Treffpunkt befinden sich Elemente, die größer oder gleich der Referenz sind. Das heißt, jedes Element von der linken Seite ist kleiner oder gleich einem Element von der rechten Seite. Daher kann das Array am Treffpunkt sicher in zwei Subarrays unterteilt werden und jedes Subarray auf ähnliche Weise rekursiv sortieren.

 def quick(data): less = [] pivotList = [] more = [] if len(data) <= 1: return data else: pivot = data[0] for i in data: if i < pivot: less.append(i) elif i > pivot: more.append(i) else: pivotList.append(i) less = quick(less) more = quick(more) return less + pivotList + more 

K-sort :: K-sort

Auf Habré wird eine Übersetzung eines der Artikel veröffentlicht, die über die Modifikation von QuickSort berichtet, die die pyramidenförmige Sortierung um 7 Millionen Elemente übertrifft. Dies ist übrigens an sich eine zweifelhafte Leistung, da die klassische pyramidenförmige Sortierung keine Leistungsrekorde bricht. Insbesondere erreicht seine asymptotische Komplexität unter keinen Umständen O (n) (ein Merkmal dieses Algorithmus).

Aber die Sache ist anders. Nach dem (und offensichtlich falschen) Pseudocode des Autors ist es im Allgemeinen nicht möglich zu verstehen, was tatsächlich die Hauptidee des Algorithmus ist. Persönlich hatte ich den Eindruck, dass die Autoren einige Gauner sind, die nach dieser Methode handelten:

1. Wir erklären die Erfindung eines Supersortieralgorithmus.
2. Wir verstärken die Aussage mit einem nicht funktionierenden und unverständlichen Pseudocode (wie klug und so klar, aber Dummköpfe können es immer noch nicht verstehen).
3. Wir präsentieren Grafiken und Tabellen, die angeblich die praktische Geschwindigkeit des Algorithmus für Big Data demonstrieren. Aufgrund des Mangels an wirklich funktionierendem Code kann niemand diese statistischen Berechnungen überprüfen oder widerlegen.
4. Wir veröffentlichen Unsinn auf Arxiv.org unter dem Deckmantel eines wissenschaftlichen Artikels.
5. GEWINN !!!

Vielleicht spreche ich vergeblich mit Leuten und tatsächlich funktioniert der Algorithmus? Kann jemand erklären, wie k-sort funktioniert?

UPD Meine pauschalen Anschuldigungen, Autoren von Betrug zu sortieren, erwiesen sich als unbegründet :) Benutzer jetsys hat den Pseudocode des Algorithmus herausgefunden, eine funktionierende Version in PHP geschrieben und mir diese in privaten Nachrichten gesendet:

Ankündigung

Es war alles eine Theorie, es ist Zeit, mit der Praxis fortzufahren. Im nächsten Artikel wird der Sortieraustausch für verschiedene Datensätze getestet. Wir werden herausfinden:

• Welche Sortierung ist die schlechteste - albern, langweilig oder langweilig?
• Helfen Optimierungen und Modifikationen der Blasensortierung wirklich?
• Unter welchen Bedingungen sind langsame Algorithmen in der Geschwindigkeit von QuickSort leicht schnell?

Und wenn wir die Antworten auf diese wichtigsten Fragen herausfinden, können wir beginnen, die nächste Klasse zu studieren - Einfügungsarten.

Referenzen

Excel-Anwendung AlgoLab , mit der Sie Schritt für Schritt die Visualisierung dieser (und nicht nur dieser) Sorten anzeigen können.

Wiki - Dumm / Handlanger , Langsam , Zwerg / Gnom , Blase / Blase , Shaker / Shaker , Ungerade / Gerade , Kamm / Kamm , Schnell / Schnell

Serienartikel

• Excel-Anwendung AlgoLab.xlsm
• Sorte austauschen
  • Vergleich der Austauschsortierung
• Insertion Sorts
• Nach Auswahl sortieren
• Sortierungen zusammenführen
• Nach Verteilung sortieren
• Hybridsortierung