Richard Hamming: Kapitel 17. Digitale Filter - IV

"Ziel dieses Kurses ist es, Sie auf Ihre technische Zukunft vorzubereiten."

Hallo Habr. Erinnern Sie sich an den großartigen Artikel „Sie und Ihre Arbeit“ (+219, 2442 Lesezeichen, 393.000 Lesungen)?

Hamming (ja, ja, selbstüberprüfende und selbstkorrigierende Hamming-Codes ) hat ein ganzes Buch geschrieben, das auf seinen Vorlesungen basiert. Wir übersetzen es, weil der Mann geschäftlich spricht.

In diesem Buch geht es nicht nur um IT, sondern auch um den Denkstil unglaublich cooler Leute. „Dies ist nicht nur eine Anklage für positives Denken. Es beschreibt Bedingungen, die die Chancen erhöhen, gute Arbeit zu leisten. “

Wir haben bereits 24 (von 30) Kapiteln übersetzt. Und wir arbeiten an einer Papierausgabe.

Kapitel 17. Digitale Filter - IV

(Vielen Dank für die Übersetzung, Andrei Pakhomov, der auf meinen Anruf im "vorherigen Kapitel" geantwortet hat.) Wer bei der Übersetzung, dem Layout und der Veröffentlichung des Buches helfen möchte - schreiben Sie in eine persönliche E-Mail oder an magisterludi2016@yandex.ru

Und jetzt wenden wir uns rekursiven Filtern zu, die die folgende Form haben:



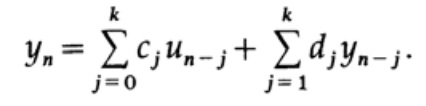
Diese Formel zeigt, dass wir Werte nur auf einer Seite des aktuellen n-ten Werts haben. Wir verwenden die vorherigen Werte des Signals und seinen Wert zum aktuellen Zeitpunkt un sowie die vorherigen Werte, die am Ausgang des Filters erhalten wurden.
Dieser klassische Ansatz ist das Ergebnis der Tatsache, dass wir das Signal häufig in Echtzeit verarbeiten und keinen Zugriff auf zukünftige Signalwerte haben.

Wenn wir uns an die Grundlagen erinnern, werden wir sehen, dass eine Zwei-Wege-Vorhersage viel genauer wäre, wenn wir „zukünftige Werte“ hätten. Um dann yn zu berechnen, würden wir auf ein System stoßen, das lineare Gleichungen sofort löst - das ist im Zeitalter billiger Computer in Ordnung. Wir werden diese Beobachtung beiseite lassen, heute zeichnen wir das Signal oft auf Band oder anderen Medien auf und verarbeiten die Daten später im Labor - und daher haben wir für einen bestimmten Zeitpunkt zukünftige Werte. Die Verwendung eines rekursiven digitalen Filters in der Bildverarbeitung wäre beispielsweise dumm, da einige der verfügbaren relevanten Informationen nicht verwendet werden.

Der nächste Aspekt, auf den Sie achten müssen, wenn Sie den vorherigen Ausgabewert als nächsten Eingang verwenden, ist das Vorhandensein von Feedback - und dies wirft automatisch das Problem der Stabilität auf. Dies ist eine Bedingung, die wir während des Entwurfs rekursiver Filter ständig überwachen müssen. Dies schränkt unsere Möglichkeiten ein. In diesem Fall bedeutet Stabilität, dass die Wirkung der Anfangsbedingungen im Endergebnis nicht überwiegt.

Bei der Arbeit mit einem linearen System haben wir festgestellt, dass unabhängig davon, welche Frequenz wir im stationären Zustand auf den Eingang des Filters angewendet haben, nur diese Frequenz am Ausgang des Filters erscheint, obwohl die Phase des Ausgangssignals relativ zur Phase des ursprünglichen Signals verschoben werden kann. Im Übergangszustand können jedoch andere Frequenzen auftreten, die sich aus der Lösung einer homogenen Differentialgleichung ergeben. Ein rekursives Filter ist nichts anderes als eine Lösung einer Differentialgleichung mit konstanten Koeffizienten für un-Terme, die eine Forcierungsfunktion bilden.

Daher nehmen wir für einen stationären Zustand (Ignorieren von Transienten) an, dass



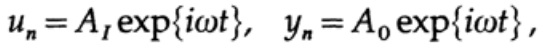
(wobei A komplexe Zahlen sein kann, um die Phasenverschiebung zu berücksichtigen), und dies führt zur Lösung des Verhältnisses A0 / A1, um die Übertragungsfunktion zu finden:



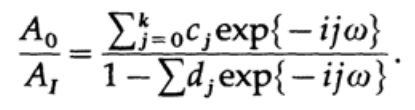
Dieser Ausdruck ist eine rationale Funktion der komplexen Variablen exp {iωt} = z im Gegensatz zu dem zuvor betrachteten nicht rekursiven Filter, bei dem die Übertragungscharakteristik ein Polynom in z war. Der theoretische Teil der Darstellung der Funktion in Form einer Expansion in einer Fourier-Reihe wird entwickelt; Bisher gibt es jedoch keine Theorie zur Darstellung von Funktionen als Relationen zweier Fourier-Reihen (ich glaube, es gibt keine Gründe, warum eine solche Theorie möglicherweise nicht existiert). Daher sind Entwurfsmethoden derzeit nicht systematisch (was Kaiser für den Entwurf nicht rekursiver Filter getan hat), sondern eine Reihe von Tricks.

Wir haben also einen Butterworth-Filter, zwei Arten von Chebyshev-Filtern (abhängig vom Vorhandensein derselben Welligkeit in den Durchlass- und Unterdrückungsbändern) und einen elliptischen Filter (der aufgrund der Verwendung elliptischer Funktionen so genannt wird), der in beiden Bändern dieselbe Welligkeit aufweist.



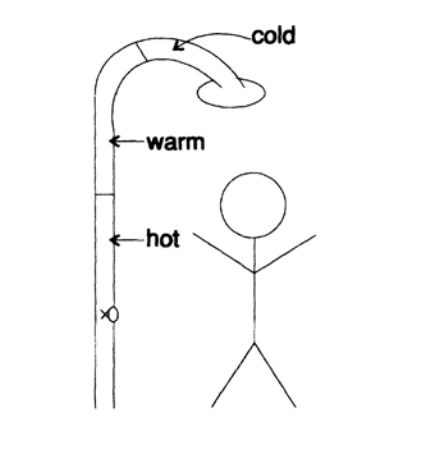Abbildung 17.1

Ich werde nur auf das Thema Feedback eingehen. Um das Feedback-Problem zu verdeutlichen, erzähle ich Ihnen eine Geschichte über mich. Es war einmal, als ich an einer Reihe von sechs halbstündigen Fernsehshows über Computer und Computer teilnahm. Die Dreharbeiten fanden hauptsächlich in San Francisco statt. Ich war oft dort und hatte die Angewohnheit, im selben Zimmer im selben Hotel zu wohnen - es ist großartig, das Zimmer in allen Details zu kennen, wenn es bereits spät in der Nacht ist und Sie müde sind oder wenn Sie mitten in der Nacht aufstehen müssen - daher der Wunsch, im selben Zimmer zu bleiben das Zimmer.

Es ist großartig, dass der Klempner die Dusche an große Rohre angeschlossen hat (Abbildung 17.I). Infolgedessen drehte ich am Morgen, als ich anfing zu duschen, das Wasser zu kalt, den Wasserhahngriff mit warmem Wasser mehr, immer noch zu kalt und mehr, immer noch zu kalt und noch mehr und schließlich, als das Wasser die richtige Temperatur bekam Ich bin geblieben Natürlich wurde das Wasser immer heißer, als das Wasser, das zuvor in die Rohre gelangt war, herauskam, und ich musste aus der Dusche springen und erneut versuchen, eine geeignete Position für den Griff des Warmwasserhahns zu finden. Die Verzögerung bei der Warmwasserversorgung verursachte mir Unannehmlichkeiten. Trotz der reichen Erfahrung befand ich mich in einer klassischen Situation der Instabilität. Sie können diese Situation von einer von zwei Seiten betrachten: Entweder war meine Reaktion zu stark (ich war sehr unhöflich in meinen Handlungen) oder die Signalerkennung war zu spät (ich war zu voreilig beim Einstellen des Wasserhahns). Der gleiche lang anhaltende Effekt! Ich hatte noch nie mit langen Verzögerungen zu kämpfen, daher begann mein Morgen jeden Tag mit Unannehmlichkeiten! In diesem anschaulichen Beispiel können Sie das Wesentliche der Instabilität betrachten.

Ich werde hier nicht auf das Design rekursiver Filter eingehen. Ich stelle nur fest, dass ich während des Kampfes mit Korrekturformeln für die numerische Lösung gewöhnlicher Differentialgleichungen unabhängig eine Theorie entwickelt habe.

Der Korrektor in der Prädiktor-Korrektor-Methode hat die Form



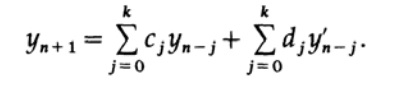
Wir sehen, dass nun die Koeffizienten uj des rekursiven Filters die Ableitungen yn 'der Filterausgabe sind, die aus der Differentialgleichung entnommen werden. Herkömmliche nicht rekursive Filter haben keine Rückkopplungsschleife - die berechneten yn-Werte werden später nicht auf der rechten Seite des Ausdrucks angezeigt. In Differentialgleichungen erscheinen sie sowohl in der Rückkopplungsschleife als auch in ihren Ableitungen und bilden dadurch eine weitere Rückkopplungsschleife, die normalerweise nicht linear ist. Daher ist die Stabilität im Bereich der Lösung von Differentialgleichungen ein komplizierteres Thema als im Bereich der rekursiven Filter.

Solche rekursiven Filter werden oft als "Filter mit unendlicher Impulsantwort" (IIR-Filter) bezeichnet, da eine einzelne Störung durch die Rückkopplungsschleife wiedergegeben wird, die exponentiell abfällt und nur dann, wenn das Filter stabil ist. Ich wäre nicht ich selbst, wenn ich mich nicht gefragt hätte, ob alle rekursiven Filter diese Eigenschaft haben sollten. Bald fand ich das gegenteilige Beispiel. In Wahrheit ist dies nicht die Art von Filter, die Sie normalerweise entwerfen, aber dieses Beispiel zeigt, dass diese Aussage oberflächlich ist. Wenn Sie sich fragen, ob alles, was Sie sagen, wahr ist, werden Sie überrascht sein, wie viele Dinge sich selbst in gut gestalteten Bereichen als falsch herausstellen!

In Kapitel 26 werde ich mich mit der Arbeit mit Experten befassen. Sie sehen nun ein Beispiel dafür, was zu oft passiert. Den Experten wurde im Klassenzimmer etwas gesagt, als sie noch Schüler waren, und sie stellten keine Fragen, sie nahmen es einfach als Tatsache. Und sie reproduzieren diese akzeptierte Tatsache ständig, ohne zu prüfen, ob sie wahr ist oder nicht, insbesondere in Bezug auf das Problem, das sie derzeit zu lösen versuchen.

Lassen Sie mich jetzt eine andere Geschichte erzählen. Eine Dame aus der Mathematikabteilung der Laboratories Labs Bella tanzte mit einem der Physiker auf einer Wochenendparty einen Square Dance und am Montagmorgen erwähnte sie mir auf dem Flur ein Problem, das er hatte. Er hat die Anzahl der Impulse in einem radioaktiven Experiment bei jeweils 256 Energieniveaus gemessen, wie ich mich erinnere. Dies nennt man das Prozessspektrum. Sein Problem bestand darin, eine Ableitung der Daten zu erhalten.

Sie wissen also, dass (a) die Anzahl der Impulse eines bestimmten Energieniveaus eine Kurve mit Diskontinuitäten bildet und (b) die Differenzierung, um einen lokalen Winkelkoeffizienten zu erhalten, an sich keine leichte Aufgabe ist. Je mehr ich über ihre zufällige Notiz nachdachte, desto mehr hatte ich das Gefühl, dass er einen guten Helfer brauchte - das bin ich! Ich fand ihn im Telefonverzeichnis der Bell Laboratories und erklärte ihm mein Interesse und wie ich zu ihm kam. Er wollte sofort in mein Büro kommen, aber ich war stur und bestand darauf, mich in seinem Labor zu treffen. Er versuchte, sein Büro anzubieten, aber ich bestand immer noch auf seinem Labor. Warum? Um seine Fähigkeiten zu bewerten und zu entscheiden, ob sein Problem meine Zeit und Mühe wert ist, da es versprach, eine harte Nuss zu knacken. Er hat den Test vom Labor mit Brillanz bestanden - es wurde klar, dass er ein sehr kompetenter Experimentator war.

Er war fast an der Grenze seiner Möglichkeiten - Daten wurden eine Woche lang gesammelt, und die Strahlungsquelle wurde von vielen Bildschirmen verdeckt. Es schien nicht so, als könnten Sie etwas anderes tun, um genauere Daten zu sammeln. Außerdem wurde ich bald überzeugt, obwohl ich nur wenige Details kannte, dass sein Experiment sowohl für die Physik als auch für die Bell Laboratories wichtig war. Also nahm ich diese Aufgabe an. Moral: Bis zu einem gewissen Grad können Sie die Aufgaben auswählen und bearbeiten, die Sie für wichtig halten.

Offensichtlich war dies ein Glättungsproblem, und Kaiser hat mich tatsächlich nur geschult. Was könnte also besser sein, als den Experimentator zu Kaiser zu bringen und Kaiser zu bitten, einen geeigneten Differenzierungsfilter zu entwerfen? Die Probleme begannen sofort. Kaiser dachte immer an das Signal als Funktion der Zeit und an die Fläche unter der Kurve als Energie, und in diesem Fall war die Energie eine unabhängige Variable! Zu diesem Zeitpunkt wiederholte sich das Problem mit Kaiser, bis ich ihm direkt sagte: "Nun, seine Energie ist Zeit und seine Messungen, Impulse, diese Spannung." Erst danach konnte Kaiser das Problem lösen.

Der Fluch der Experten liegt in ihrem begrenzten Verständnis dessen, was sie tun können. Ich habe Ihnen gegenüber erwähnt, dass Kaiser ein sehr fähiger Mensch ist, aber seine Erfahrung, wie sie oft bei Experten vorkommt, hat seine Vision eingeschränkt. Können Sie es wiederum besser machen? Ich hoffe, diese Geschichten helfen Ihnen, diese Falle zu umgehen.

Wie ich zuvor bemerkt habe, befindet sich das Spektrum des Nutzsignals normalerweise am unteren Rand des Nyquist-Bandes, und das Rauschspektrum ist über das Nyquist-Band verteilt, sodass wir die Grenzfrequenz zwischen dem Nutzsignal des Physikers und dem flachen weißen Rauschen ermitteln mussten. Wie finde ich sie? Zuerst habe ich ein theoretisches Modell des Experiments aus dem Kopf des Physikers ausprobiert, der sich in seinem Kopf befand - es waren viele schmale Spektrallinien in Form von Gaußschen Funktionen über einer breiten Gaußschen Funktion (ich bezweifelte, dass dies eine Cauchy-Verteilung war, argumentierte aber nicht damit, da der Unterschied wäre angesichts der Art der Daten, die wir hatten, sehr klein). Also haben wir diese Verteilung simuliert und er hat eine bestimmte Menge synthetischer Daten vorbereitet, die diesem Modell entsprechen. Eine schnelle Spektralanalyse des Signals durch schnelle Fourier-Transformation zeigte, dass sich das Signal im unteren 1/20 des Nyquist-Bandes befindet. Außerdem haben wir seine experimentellen Daten auf die gleiche Weise verarbeitet und den gleichen Grenzfrequenzort erhalten! Was für ein Glück! (Vielleicht sollte das Glück auf die Fähigkeiten des Experimentators zurückgeführt werden). Es war einmal, Theorie und Praxis kamen zusammen! Es stellte sich heraus, dass wir 95% des Rauschens herausfiltern konnten. Schließlich schrieb Kaiser für ihn ein Programm, das einen Filter für eine bestimmte Grenzfrequenz synthetisierte, der vom Experimentator eingestellt wurde.

Das Programm (1) berechnete ein geeignetes Differenzierungsfilter, (2) schrieb ein Programm zur Berechnung der geglätteten Ausgabe und verarbeitete dann (3) die Daten mit diesem Filter ohne Eingreifen des Physikers.

Später fing ich einen Physiker auf, indem ich die Grenzfrequenz für verschiedene Teile der Energieniveaudaten anpasste, die in einer Reihe von Messungen erhalten wurden, und musste ihn daran erinnern, dass es bestimmte „Freiheitsgrade“ gibt und dass er keine ehrliche Datenverarbeitung durchführt. Es wurde viel problematischer, wenn die Dinge gut liefen, ihn davon zu überzeugen, das Beste aus seinen Daten herauszuholen (was sehr teuer war) - er sollte mit den Quadratwurzeln seiner Impulse arbeiten, da sie die gleiche Varianz hatten. Schließlich verstand er das und tat es. Er und Kaiser haben in diesem Bereich ein klassisches Werk geschrieben, das die Tür zu neuen Dingen öffnete, die getan werden konnten.

Mein Beitrag Identifizieren Sie zuerst das Problem, bringen Sie dann die richtigen Leute zusammen, beobachten Sie Kaiser, um ihn mit der Tatsache zu konfrontieren, dass Filterung nicht nur für Signale als Funktionen der Zeit erforderlich ist, und erinnern Sie sie schließlich an das, was sie aus Statistiken wussten (oder haben sollten) zu wissen, aber vielleicht wussten sie es nicht).

Aus meiner Sicht scheint mir der Bedarf an einer solchen Rolle zu steigen, da die Menschen immer mehr Experten in immer engeren Wissensgebieten werden. Jemand muss einen weiten Horizont einhalten und sicherstellen, dass die Dinge ehrlich gemacht werden. Ich glaube, ich bin nach einer sehr langen Ausbildung unter der Leitung von John Tukey zu dieser Rolle gekommen, zusätzlich zu einer guten Grundlage in Form eines universellen wissenschaftlichen Werkzeugs namens Mathematik. Ich werde in Kapitel 23 über die Natur der Mathematik sprechen.

Der größte Teil der Signalverarbeitung erfolgt über Signale im Laufe der Zeit. Gleichzeitig sind die meisten digitalen Filter für kleine, hochspezialisierte Studien konzipiert, die nicht unbedingt mit Signalen im Laufe der Zeit verbunden sind. Hier werde ich Sie bitten, in Zukunft vorsichtig zu sein. Angenommen, Sie führen das Geschäft ganz oben und sind an Daten interessiert, die frühere Arbeitskosten für Geräte anzeigen. Es werden verrauschte Daten sein, aber Sie möchten im üblichen Sinne immer noch verstehen, was in der Organisation passiert - welche langfristigen Prozesse stattfinden - diejenigen, die so langsam sind, dass die Leute sie verstehen, wenn sie bereits geschehen, aber dennoch verstehen Fangen, was von grundlegender Bedeutung ist, wenn Sie ein guter Manager sein wollen. Sie benötigen einen digitalen Filter, um die Daten zu glätten und Hinweise auf den Trend zu sehen, falls vorhanden. Sie möchten keinen Trend finden, der nicht existiert, aber wenn er existiert, möchten Sie wirklich wissen, was er vorher war, um vorherzusagen, wie er in naher Zukunft wahrscheinlich sein wird. In der Tat möchten Sie Änderungen in der Trendneigung sehen, wenn die Daten es Ihnen erlauben, sie zu sehen. Einige Signale, wie z. B. die Feuerkraft in Bezug auf die Verschiebung des Schiffes, sind nicht an die Zeit gebunden, können jedoch viel über den aktuellen Zustand der Flotte aussagen. Natürlich können Sie diese Beziehung als Funktion der Zeit studieren.

Zu Beginn Ihrer Karriere können Sie eine Vielzahl von Low-Level-Digitalfiltern für Signale als Funktion der Zeit verwenden und nicht nur, um die Dinge besser zu verwalten. Daher argumentiere ich, dass Sie wahrscheinlich viel mehr digitale Filter für solche nicht standardmäßigen Dinge synthetisieren als für das Verkleinern von Radardaten und ähnlichen klassischen Anwendungen. Normalerweise können Sie in neuen Wissensanwendungen die höchste Rendite erzielen.

Lassen Sie mich einige Bedenken hinsichtlich des falschen Einsatzes intelligenter Werkzeuge äußern. Ich werde in Kapitel 27 ausführlicher auf statistische Themen eingehen. Die Fourier-Expansionsanalyse nimmt die Linearität des zugrunde liegenden Modells an. Sie können es für leicht nichtlineare Fälle verwenden, aber meistens schlägt eine gekonnt durchgeführte Analyse durch Fourier-Expansion fehl, da das untersuchte Phänomen zu nichtlinear ist. Ich habe gesehen, wie Millionen von Dollar verschwendet wurden, als es für Außenstehende ziemlich offensichtlich war, dass Nichtlinearitäten die gesamte lineare Analyse durch Approximation durch Fourier-Reihen verzerren würden. Als sie darauf hinwiesen, war ihre Antwort, dass sie nicht wussten, wie sie anders vorgehen könnten, also machten sie weiter das Falsche! Und ich übertreibe hier nicht.



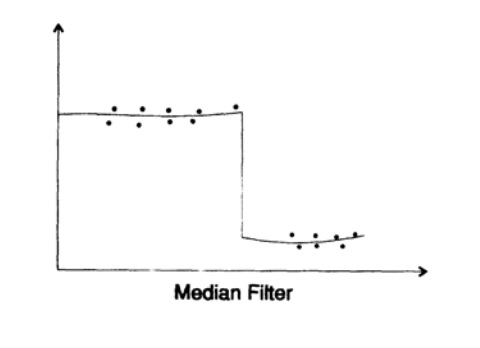Abbildung 17.2

Was ist mit nichtlinearen Filtern? Die Möglichkeiten hier sind endlos und hängen natürlich von dem Problem ab, mit dem Sie sich befassen. Ich werde mich nur mit einem von ihnen befassen, dem Medianfilter.Sie betrachten die Medianfilterausgabe für einen bestimmten Datensatz. Mal sehen, wie es in der Praxis funktioniert. Zunächst stellen wir fest, dass versucht wird, lokales Rauschen auszugleichen. Wie verhält sich der Filter jedoch am Unterbrechungspunkt (Abb. 17.2)?

Bei einer ungeraden Anzahl von Elementen im Medianfilter sehen Sie, dass die Ausgabe des Filters auf der oberen Ebene bleibt, bis mehr als die Hälfte der Punkte am Eingang des Filters auf der unteren Ebene liegen. Danach "springt" die Ausgabe des Filters nach unten. Er wird die Pausen gut genug verfolgen und nicht versuchen, sie vollständig zu glätten! In einigen Fällen ist dies genau die Art von Filter, die zu Ihnen passt - lokales Rauschen wird geglättet, während plötzliche Änderungen des Zustands des untersuchten Systems nicht verloren gehen.

Ich wiederhole, dass die Analyse nach Fourier-Reihen linear ist, während es eine große Anzahl nichtlinearer Filter gibt, aber die Theorie für nichts anderes als einen Medianfilter gut entwickelt ist. Das Kalman-Filter ist ein weiteres Beispiel für die Verwendung eines teilweise nichtlinearen Filters, der nichtlineare Teil ist die unabhängige „Anpassung“ des Filters an das Signal.

Schließlich ist hier eine weitere grundlegende Beobachtung, die ich beim Studium digitaler Filter gemacht habe. Als ich eines Tages ein Buch über Fourier-Integrale studierte, fand ich einen Satz, der besagte, dass die Variation einer Funktion multipliziert mit der Variation ihrer Transformation größer als eine bestimmte Konstante sein sollte. Ich fragte mich: "Was ist es außer dem berühmten Prinzip der Unsicherheit der Quantenmechanik"? Ja, jede lineare Theorie sollte ein Unsicherheitsprinzip haben, das konjugierte Variablen verbindet. Sobald Sie den linearen Ansatz wählen und das CM die absolute Additivität der Eigenzustände bestätigt, sollten Sie das Prinzip der Unsicherheit entdecken. Die lineare Invarianz der Zeit führt automatisch zu den Eigenfunktionen e ^ iω (t). Sie führen sofort zu Fourier-Reihen und haben wiederum das Prinzip der Unsicherheit.Es ist, als ob Sie eine blau getönte Brille tragen. Was auch immer Sie betrachten, es sollte einen bläulichen Farbton haben!

Daher sind Sie sich nicht sicher, ob das berühmte Prinzip der CM-Unsicherheit existiert oder nicht. Vielleicht ist dies nur der Effekt der impliziten Linearität des Systems.

Nur wenige Menschen wollen glauben, dass das, was wir sehen, davon abhängt, auf welcher Seite wir uns dem Problem nähern! Sehr oft sehen wir, was wir sehen wollen, und deshalb sollten Sie überall einen wissenschaftlichen Ansatz verfolgen und an Ihren eigenen Überzeugungen zweifeln.
Um dies klar zu demonstrieren, werde ich Eddingtons Geschichte über Fischer wiederholen. Sie fischten im Netz und als sie die Größe der im Netz gefangenen Fische untersuchten, stellten sie fest, dass es im Meer eine Mindestgröße von Fischen gab.

Wenn Sie ab und zu nicht an den verabschiedeten Regeln zweifeln, werden Sie höchstwahrscheinlich in keinem Bereich führend. Wenn Sie dagegen an allem zweifeln, werden Sie gelähmt sein und nichts tun . Wann man zweifelt, wann man die Grundlagen lernt, wann man selbst denkt und wann man einfach weitermacht und die Dinge so nimmt, wie sie sind, ist eine Frage des Denkstils, und ich kann keine einfache Formel zur Lösung dieses Problems geben. Sie müssen aus Ihrer eigenen Erfahrung lernen. Große Gewinne werden normalerweise nach wesentlichen Änderungen der zugrunde liegenden Annahmen erzielt, auf denen der Bereich basiert. Der Stand unseres Wissens bestimmt das Gleichgewicht zwischen verschiedenen Aspekten der Forschung. Es scheint, dass wenn Sie jung sind, Intuition und Einsicht mehr Zeit haben, um sich auszuzahlen, aber wenn Sie alt sind,Dafür bleibt weniger Zeit und Sie sollten sich wahrscheinlich auf das konzentrieren, was Ihnen bereits zur Verfügung steht.

Fortsetzung folgt...

Wer bei der Übersetzung, dem Layout und der Veröffentlichung des Buches helfen möchte - schreiben Sie in einer persönlichen E-Mail oder per E-Mail an magisterludi2016@yandex.ru

Übrigens haben wir auch die Übersetzung eines weiteren coolen Buches veröffentlicht - „Die Traummaschine: Die Geschichte der Computerrevolution“ )