Geekly articles weekly

Software-Implementierung des IIR-Filters im Informationsmesskanal

Informationen über den Zustand der Umgebung oder beispielsweise eines bestimmten Steuerobjekts können erhalten werden, indem die aktuellen Werte von Parametern gemessen werden, die bestimmte Eigenschaften der Umgebung oder des Objekts charakterisieren. Um solche Informationen auf technischem Wege zu empfangen, zu verarbeiten und zu übertragen, muss der Wert des gemessenen Parameters von automatischen Messgeräten in ein Messinformationssignal umgewandelt werden. Implementieren Sie dazu den Informationsmesskanal ( IIC ) als eine Kombination technischer Mittel, von denen jedes seine spezifische Funktion erfüllt, beginnend mit der Wahrnehmung des Messwerts und endend mit dem Empfang der Messinformationen in einer Form, die für die menschliche Wahrnehmung oder für deren weitere Verarbeitung geeignet ist. Und alles wäre in Ordnung, aber entlang des Informationspfads wird die Interferenz e (t) dem Nutzsignal y (t) der Messinformationen überlagert - eine zufällige Funktion der Zeit, die den zufälligen Fehler des Messwandlers, elektrische Aufnehmer in den Verbindungsdrähten und zufällige Welligkeiten simulieren kann gemessener Parameter und andere Faktoren.

Auf dieser Grundlage ergibt sich das Problem der primären Verarbeitung von Informationen im IIC - Filtern des Signals y (t) der Messinformationen aus zufälligen Interferenzen e (t). Grundsätzlich basieren Filtermethoden auf der Differenz der Frequenzspektren der Funktionen y (t) und e (t), und die Interferenz wird als hochfrequenter angesehen.

Die Synthese des implementierten optimalen Filters ist eine komplexe Aufgabe, deren Lösung die genaue Spezifikation der Eigenschaften des Nutzsignals und der Interferenz erfordert. Daher wird in der Praxis die Übertragungsfunktion des Filters normalerweise spezifiziert und auf die parametrische Synthese unter Verwendung einfacher Filteralgorithmen beschränkt.

Filtrationsmethoden werden sowohl auf Software- als auch auf Hardwareebene durchgeführt. Beispielsweise ist es beim BMP280 (BOSCH) -Sensor möglich, einen IIR-Filter auf Hardwareebene anzuschließen und gegebenenfalls den Filterkoeffizienten k zu ändern [1].

IIR-Filter


Filter mit unendlicher Impulsantwort sind rekursive Filter und berechnen das Ausgangssignal basierend auf den Werten vorheriger Eingangs- und Ausgangsproben. Theoretisch erreicht die Impulsantwort eines IIR-Filters niemals Null, sodass die Dauer des Ausgangs unendlich ist.

Im Allgemeinen schreiben wir den Algorithmus zum Filtern eines eindimensionalen skalaren Digitalfilters als [2]:

y[n]=T(x[n],x[n−1],...,x[n−M],y[n−1],...,y[n−N],n), (1),
Dabei ist T eine Skalarfunktion einer Variablen.

Die Funktion T hängt vom aktuellen Eingangssignal x [n] und den vorherigen: M Abtastwerten des Eingangssignals ab und N Abtastwerte des Ausgangssignals

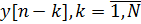
Die Ausgabe des IIR-Filters wird durch eine Differenzgleichung der Form beschrieben:

(2)
wobei x [n], y [n] die Eingabe bzw. Ausgabe des Filters ist, { ak} Ist die Menge der direkten Koeffizienten, M ist die Anzahl der direkten Koeffizienten, { bk} Ist eine Menge von inversen Koeffizienten, N ist die Anzahl von inversen Koeffizienten.

Wenn wir die z-Transformation auf beide Seiten von Gleichung (2) anwenden, erhalten wir:

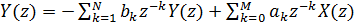
(3).

Dann sieht die Übertragungsfunktion des Filters folgendermaßen aus:

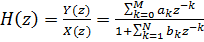
(4)

Algorithmus zum Filtern eines eindimensionalen IIR-Filters


Im Allgemeinen sieht der Filteralgorithmus für ein eindimensionales skalares stationäres rekursives Filter folgendermaßen aus:

y[n]=T(x[n],y[n−1]). (5)

Wir schreiben nun die Differenzgleichung für den IIR-Filter in der Form [1]:

(6)
wobei k der Filterkoeffizient ist;
oder
y[n]=ay[n−1]+bx[n](7)
wo Sind die inversen und Vorwärtsfilterkoeffizienten.

Aus (7) ist ersichtlich, dass bei k = 1 das Ausgangssignal des Filters den Eingang wiederholt, und wenn der Filterkoeffizient k zunimmt, tendiert das Gewicht des vorherigen gefilterten Signals zu 1 und das Gewicht des gemessenen Wertes zu 0.

Der Algorithmus (6) ist als Beispiel für den Informationsmesskanal für den absoluten Atmosphärendruck für den BMP280-Sensor auf Softwareebene in der Entwicklungsumgebung Arduino Software (IDE) implementiert, wobei 1 aufgeführt ist. Das elektrische Verbindungsdiagramm der IIC-Komponenten ist in Abb. 1. Die allgemeine Ansicht des absoluten atmosphärischen Drucks des Prototyps IIC ist in Abb. 1 dargestellt. 2. Der Prototyp bietet die Möglichkeit, den Filterkoeffizienten im Bereich von 1 bis 50 in Schritten von 1 durch Drehen des Knopfes des Potentiometers zu ändern. Das Vorzeichen der Flüssigkristallanzeige zeigt den gemessenen Druckwert (für k = 1) oder den gefilterten Wert (für k = 2 ... 50) und den Filterkoeffizienten k.

Listing 1
//    () // -  - //https://github.com/orgua/iLib/blob/master/src/i2c.h #include "i2c.h" //https://github.com/orgua/iLib/blob/master/src/i2c_BMP280.h #include "i2c_BMP280.h" //https://github.com/arduino-libraries/LiquidCrystal #include <LiquidCrystal.h> //https://github.com/orgua/iLib/tree/master/examples/i2c_BMP280 BMP280 bmp280; const int rs = 12, en = 11, d4 = 6, d5 = 5, d6 = 4, d7 = 3; //const int rs = PB4, en = PB3, d4 = PD6, d5 = PD5, d6 = PD4, d7 = PD3; LiquidCrystal lcd(rs, en, d4, d5, d6, d7); float pascal_f = 100500; float filter_K = 1; const int analogInPin = A0; //    int sensorValue = 0; //   int outputValue = 0; void setup() { Serial.begin(9600); //Serial.print("Probe BMP280: "); if (bmp280.initialize()) { //Serial.println("Sensor found"); ; } else { Serial.println("Sensor missing"); while (1) {} } bmp280.setEnabled(0); bmp280.triggerMeasurement(); bmp280.setFilterRatio(0); lcd.begin(16, 2); lcd.setCursor(0, 0); lcd.print("measure"); lcd.setCursor(7, 1); lcd.print("Pa"); lcd.setCursor(10, 0); lcd.print("filter"); } void loop() { float temperature; float pascal, hpascal; sensorValue = analogRead(analogInPin); outputValue = map(sensorValue, 0, 1023, 1, 50); filter_K = outputValue; bmp280.awaitMeasurement(); bmp280.getTemperature(temperature); temperature -= 1.7; // bmp280.getPressure(pascal); pascal -= 50;// hpascal = pascal/100.; bmp280.triggerMeasurement(); pascal_f = (pascal_f * (filter_K - 1) + pascal) / filter_K; //(6) Serial.println(pascal_f,0); if(pascal_f < 100000) lcd.setCursor(6, 1); lcd.print(" "); lcd.setCursor(0, 1); lcd.print(pascal_f,0); if(filter_K < 10) lcd.setCursor(13, 1); lcd.print(" "); lcd.setCursor(10, 1); lcd.print(filter_K,1); delay(300); }



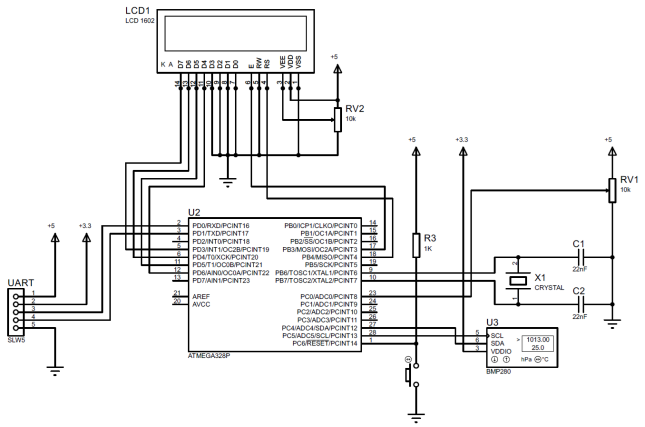Abb. 1 - Schaltplan der Komponenten des Prototyps IIC


Abb. 2 - Gesamtansicht des Prototyps IIC

Python-Skript zur Untersuchung von IIR-Filtern


Listing 2 zeigt ein Python-Skript zur Untersuchung von IIR-Filtern. Der Filterkoeffizient k wird in das Skript geschrieben. Die gemessenen Druckwerte werden nacheinander vom virtuellen COM-Port gelesen und gefiltert. Die gemessenen und gefilterten Werte des gemessenen Parameters werden in Echtzeit im Grafikfenster und auf der Konsole angezeigt. Die Ergebnisse des Experiments werden von der Tabelle in einer Datei aufgezeichnet, und die Zeitleisten der gemessenen und gefilterten Werte werden im Grafikfenster angezeigt.

Listing 2:
 import numpy as np import matplotlib.pyplot as plt import serial from drawnow import drawnow import datetime, time k = 6.0 #  + 1 filter_K = 1 + k #     def cur_graf(): plt.title("BMP280") plt.ylim( 100450, 100510 ) plt.plot(nw, lw1, "r.-", label='') plt.plot(nw, lw1f, "b.-", label='') plt.legend(loc='best') plt.ylabel(r'$, $') plt.xlabel(r'$ \ $') plt.grid(True) #      def all_graf(): plt.close() fig=plt.figure() ax = fig.add_subplot(111) fig.subplots_adjust(top=0.85) ax.set_title(" BMP280\n" + str(count_v) + "-  " + "(" + now.strftime("%d-%m-%Y %H:%M") + ")") ax.set_ylabel(r'$, $') ax.set_xlabel(r'$ \ $' + '; (  : {:.6f}, c)'.format(Ts)) ax.text(0.95, 0.03, " : " + str(filter_K) + "\n", verticalalignment='bottom', horizontalalignment='right', transform=ax.transAxes, color='black', fontsize=14) plt.plot( n, l1, "r-", label='') plt.plot( n, l1f, "b-", label='') plt.legend(loc='best') plt.grid(True) plt.show() #   #    str_m = input("  : ") m = eval(str_m) #    mw = 16 #    ser = serial.Serial() ser.baudrate = 9600 port_num = input("   : ") ser.port = 'COM' + port_num ser #   try: ser.open() ser.is_open print(" : " + ser.portstr) except serial.SerialException: print("   : " + ser.portstr) raise SystemExit(1) #  l1 = [] #    l1f = [] #     t1 = [] #     lw1 = [] #     lw1f= [] #      n = [] #     nw = [] #      #      filename = 'count.txt' in_file = open(filename,"r") count = in_file.read() count_v = eval(count) + 1 in_file.close() in_file = open(filename,"w") count = str(count_v) in_file.write(count) in_file.close() filename = count + '_' + filename out_file = open(filename,"w") #      print("\n:\n") print("n -  ;") print("P - , ;") print("\n   \n") print('{0}{1}\n'.format('n'.rjust(4),'P'.rjust(10))) #     #  #   #       i = 0 while i < m: n.append(i) nw.append(n[i]) if i >= mw: nw.pop(0) line1 = ser.readline().decode('utf-8')[:-2] t1.append(time.time()) if line1: l1.append(eval(line1)) lw1.append(l1[i]) if i : l1f.append( (l1f[i-1]*(filter_K - 1) + l1[i])/filter_K ) #(6) lw1f.append(l1f[i]) else : l1f.append(l1[i]) lw1f.append(l1f[i]) if i >= mw: lw1.pop(0) lw1f.pop(0) print('{0:4d} {1:10.2f} {2:10.2f}'.format(n[i],l1[i],l1f[i]) ) drawnow(cur_graf) i += 1 #   ser.close() ser.is_open time_tm = t1[m - 1] - t1[0] print("\n  : {0:.3f}, c".format(time_tm)) Ts = time_tm / (m - 1) print("\n  : {0:.6f}, c".format(Ts)) #    print("\n    {}\n".format(filename)) for i in np.arange(0,len(n),1): count = str(n[i]) + "\t" + str(l1[i]) + "\n" out_file.write(count) #    out_file.close() out_file.closed #    now = datetime.datetime.now() #     all_graf() end = input("\n Ctrl-C,   ")


Versuchsergebnisse


   : 33    : 6  : COM6 : n -  ; P - , ;     n P 0 100490.00 100490.00 1 100488.00 100489.71 2 100487.00 100489.33 3 100488.00 100489.14 4 100488.00 100488.97 … 30 100486.00 100488.14 31 100492.00 100488.70 32 100489.00 100488.74   : 16.028, c   : 0.500875, c     275_count.txt  Ctrl-C,





Schlussfolgerungen


Der obige Filteralgorithmus ist in der Softwareimplementierung sehr einfach und kann in der Praxis in IICs verwendet werden, die den in diesem Artikel beschriebenen ähnlich sind.
Losikhin D.A., s.v. Cafe STADT .

Informationsquellen


  1. Digitaler Drucksensor BMP280
  2. Filter für unendliche Impulsantwort

Source: https://habr.com/ru/post/de414943/

More articles:


All Articles