In dieser Artikelserie lernen Sie die Grundprinzipien der funktionalen Programmierung kennen und verstehen, was es bedeutet, „funktional zu denken“ und wie sich dieser Ansatz von der objektorientierten oder imperativen Programmierung unterscheidet.

Nachdem Sie einige der Gründe gesehen haben, warum Sie F # verwenden sollten, lesen Sie im Artikel „ Eintauchen in F #. Ein Leitfaden für C # -Entwickler “, treten Sie einen Schritt zurück und diskutieren Sie die Grundlagen der funktionalen Programmierung. Was bedeutet „funktionale Programmierung“ wirklich und wie unterscheidet sich dieser Ansatz von der objektorientierten oder imperativen Programmierung?
Änderung der Denkweise (Intro)
Es ist wichtig zu verstehen, dass funktionale Programmierung nicht nur ein separater Programmierstil ist. Dies ist eine völlig andere Denkweise in der Programmierung, die sich vom „traditionellen“ Ansatz ebenso stark unterscheidet wie die gegenwärtige OOP (im Smalltalk-Stil) von einer traditionellen imperativen Sprache wie C.
Mit F # können Sie nicht funktionierende Codierungsstile verwenden, was den Programmierer dazu verleitet, seine vorhandenen Gewohnheiten beizubehalten. Sie können in F # so programmieren, wie Sie es gewohnt sind, ohne das Weltbild radikal zu verändern und ohne zu wissen, was Sie verpassen. Um jedoch das Beste aus F # herauszuholen und zu lernen, wie man sicher in einem funktionalen Stil im Allgemeinen programmiert, ist es sehr wichtig zu lernen, funktional und nicht zwingend zu denken.
Der Zweck dieser Artikelserie ist es, dem Leser zu helfen, den Hintergrund der funktionalen Programmierung zu verstehen und seine Denkweise zu ändern.
Dies wird eine ziemlich abstrakte Serie sein, obwohl ich viele kurze Codebeispiele verwenden werde, um einige Punkte zu demonstrieren. Wir werden folgende Themen behandeln:
- Mathematische Funktionen . Der erste Artikel stellt die mathematischen Konzepte vor, die funktionalen Sprachen zugrunde liegen, und die Vorteile, die dieser Ansatz mit sich bringt.
- Funktionen und Werte . Im Folgenden werden Funktionen und Werte vorgestellt, erläutert, wie sich „Werte“ von Variablen unterscheiden und welche Ähnlichkeiten zwischen Funktionen und einfachen Werten bestehen.
- Typen . Dann gehen wir zu den Haupttypen über, die mit Funktionen arbeiten: primitive Typen wie Zeichenfolge und Int, Einheitentyp, Funktionstypen und generische Typen.
- Funktioniert mit mehreren Parametern . Ich werde die Konzepte von "Currying" und "Teilanwendung" weiter erläutern. An diesem Ort wird jemandes Gehirn verletzt, besonders wenn diese Gehirne nur eine zwingende Vergangenheit haben.
- Definition von Funktionen . Anschließend werden mehrere Beiträge vielen verschiedenen Möglichkeiten zum Definieren und Kombinieren von Funktionen gewidmet.
- Signaturen von Funktionen . Das Folgende ist ein wichtiger Beitrag zum kritischen Wert von Funktionssignaturen, was sie bedeuten und wie Signaturen verwendet werden, um den Inhalt von Funktionen zu verstehen.
- Organisation von Funktionen . Wenn klar wird, wie Funktionen erstellt werden, stellt sich die Frage: Wie können Sie sie organisieren, um sie für den Rest des Codes zugänglich zu machen?
Mathematische Funktionen
Die funktionale Programmierung ist von der Mathematik inspiriert. Mathematische Funktionen haben eine Reihe sehr netter Funktionen, die funktionale Sprachen zu implementieren versuchen.
Beginnen wir mit einer mathematischen Funktion, die einer Zahl 1 hinzufügt.
Add1(x) = x+1
Was bedeutet dieser Ausdruck wirklich? Es sieht ziemlich einfach aus. Dies bedeutet, dass es eine solche Operation gibt, die eine Zahl nimmt und 1 hinzufügt.
Fügen Sie eine Terminologie hinzu:
- Die Menge der gültigen Eingabefunktionswerte wird als Domäne (Bereich) bezeichnet. In diesem Beispiel könnten es viele reelle Zahlen sein, aber wir werden das Leben einfacher machen und uns hier auf ganze Zahlen beschränken.
- Die Menge der möglichen Ergebnisse der Funktion (Wertebereich) wird als Bereich (technisch das Codomänenbild ) bezeichnet. In diesem Fall gibt es auch viele ganze Zahlen.
- Eine Funktion wird als Zuordnung (in der ursprünglichen Zuordnung ) von Domäne zu Bereich bezeichnet. (Das heißt, vom Geltungsbereich zum Geltungsbereich.)
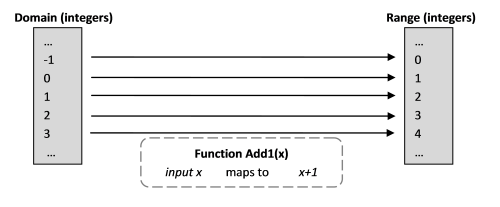
So sieht diese Definition in F # aus.
let add1 x = x + 1
Wenn Sie es in F # Interactive eingeben (doppelte Semikolons nicht vergessen), sehen Sie das Ergebnis (die "Signatur" der Funktion):
val add1 : int -> int
Betrachten Sie die Schlussfolgerung im Detail:
- Die allgemeine Bedeutung ist, dass die Funktion
add1 Ganzzahlen (aus der Definitionsdomäne) mit Ganzzahlen (aus dem Wertebereich) vergleicht. - "
add1 " ist definiert als "val", kurz für "value". Hm? Was bedeutet das? Wir werden die Bedeutungen etwas später diskutieren. - Die Pfeilnotation "->" wird verwendet, um Domäne und Bereich anzuzeigen. In diesem Fall ist die Domäne vom Typ 'int', wie der Bereich.
Beachten Sie, dass der Typ nicht explizit angegeben wurde, der F # -Compiler jedoch entschieden hat, dass die Funktion mit Ints funktioniert. (Kann das geändert werden? Ja, und bald werden wir es sehen).
Schlüsseleigenschaften mathematischer Funktionen
Mathematische Funktionen haben eine Reihe von Eigenschaften, die sie stark von den Funktionen unterscheiden, die in der prozeduralen Programmierung verwendet werden.
- Eine Funktion hat immer das gleiche Ergebnis für den gleichen Eingabewert.
- Die Funktion hat keine Nebenwirkungen.
Diese Eigenschaften bieten eine Reihe bemerkenswerter Vorteile, die funktionale Programmiersprachen in ihrem Design so weit wie möglich zu realisieren versuchen. Wir werden jeden von ihnen der Reihe nach betrachten.
Mathematische Funktionen geben immer das gleiche Ergebnis auf einen bestimmten Wert zurück
In der imperativen Programmierung denken wir, dass Funktionen entweder etwas „tun“ oder etwas „zählen“. Die mathematischen Funktionen zählen nichts, es sind reine Zuordnungen von Eingabe zu Ausgabe. Tatsächlich ist eine andere Definition einer Funktion eine einfache Menge aller Zuordnungen. Zum Beispiel ist es sehr grob möglich, die Funktion "add1" (in C #) als zu definieren
int add1(int input) { switch (input) { case 0: return 1; case 1: return 2; case 2: return 3; case 3: return 4; etc ad infinitum } }
Natürlich ist es unmöglich, für jede mögliche Zahl einen Fall zu haben, aber das Prinzip ist dasselbe. Mit dieser Einstellung werden keine Berechnungen durchgeführt, sondern nur eine Suche.
Mathe funktioniert frei von Nebenwirkungen
In einer mathematischen Funktion sind die Eingabe- und Ausgabewerte logischerweise zwei verschiedene Dinge, die beide vordefiniert sind. Die Funktion ändert die Eingabe- oder Ausgabedaten nicht und ordnet einfach den vordefinierten Eingabewert aus dem Definitionsbereich dem vordefinierten Ausgabewert im Wertebereich zu.
Mit anderen Worten, eine Funktionsberechnung kann keine Auswirkungen auf die Eingabedaten oder ähnliches haben . Es sollte beachtet werden, dass die Berechnung einer Funktion nichts wirklich zählt oder manipuliert, sondern nur eine überbewertete Suche ist.
Diese „Unveränderlichkeit“ von Werten ist sehr subtil, aber gleichzeitig eine sehr wichtige Sache. Wenn ich rechne, erwarte ich nicht, dass sich Zahlen ändern, wenn sie hinzugefügt werden. Zum Beispiel, wenn ich habe:
x = 5 y = x+1
Ich erwarte nicht, dass sich x ändert, wenn ich 1 hinzufüge. Ich erwarte eine andere Zahl ( y ), und x sollte unberührt bleiben. In der Welt der Mathematik existieren ganze Zahlen bereits in einer unveränderlichen Menge, und die Funktion add1 bestimmt einfach die Beziehung zwischen ihnen.
Die Kraft der reinen Funktion
Diese Arten von Funktionen, die wiederholbare Ergebnisse haben und keine Nebenwirkungen haben, werden als „reine Funktionen“ bezeichnet, und Sie können einige interessante Dinge damit tun:
- Sie sind leicht zu parallelisieren. Angenommen, wir könnten Ganzzahlen im Bereich von 1 bis 1000 nehmen und sie auf 1000 verschiedene Prozessoren verteilen.
add1 wir jede CPU an, " add1 " für die entsprechende Nummer auszuführen, wobei sichergestellt werden muss, dass keine Interaktion zwischen ihnen erforderlich ist. Keine Schlösser, keine Mutexe, keine Semaphoren usw. - Sie können Funktionen träge verwenden und sie bei Bedarf für die Programmlogik berechnen. Sie können sicher sein, dass die Antwort genau dieselbe ist, unabhängig davon, ob die Berechnungen jetzt oder später durchgeführt werden.
- Sie können nur Funktionsberechnungen für eine bestimmte Eingabe durchführen und dann das Ergebnis zwischenspeichern, da bekannt ist, dass diese Eingabewerte dieselbe Ausgabe ergeben.
- Wenn es viele reine Funktionen gibt, können sie in beliebiger Reihenfolge berechnet werden. Auch dies kann das Endergebnis nicht beeinflussen.
Wenn es also möglich ist, reine Funktionen in einer Programmiersprache zu erstellen, können Sie sofort viele leistungsstarke Tricks erhalten. Und zweifellos kann dies alles in F # erfolgen:
- Ein Beispiel für paralleles Rechnen war die Serie „Warum F # verwenden?“. .
- Die Berechnung verzögerter Funktionen wird in der Optimierungsreihe erläutert.
- Die Ergebnisse der Caching-Funktion werden als Memoisierung bezeichnet und werden auch in der Optimierungsreihe erläutert.
- Das Fehlen der Notwendigkeit, die Ausführungsreihenfolge zu verfolgen, erleichtert die parallele Programmierung erheblich und beseitigt die Notwendigkeit von Fehlern, die durch Ändern der Reihenfolge der Funktionen oder Refactoring verursacht werden.
"Nutzlose" Eigenschaften mathematischer Funktionen
Mathematische Funktionen haben auch einige Eigenschaften, die beim Programmieren nicht sehr nützlich erscheinen.
- Eingabe- und Ausgabewerte sind unveränderlich
- Funktionen haben immer einen Eingang und einen Ausgang.
Diese Eigenschaften spiegeln sich im Design funktionaler Programmiersprachen wider. Es lohnt sich, sie separat zu betrachten.
Eingabe- und Ausgabewerte sind unveränderlich
Unveränderliche Werte scheinen theoretisch eine gute Idee zu sein, aber wie kann man wirklich arbeiten, wenn es keine Möglichkeit gibt, eine Variable auf herkömmliche Weise zuzuweisen?
Ich kann Ihnen versichern, dass dies kein so großes Problem ist, wie Sie sich vorstellen können. In dieser Artikelserie wird deutlich, wie dies in der Praxis funktioniert.
Mathematische Funktionen haben immer einen Eingang und einen Ausgang.
Wie aus den Diagrammen ersichtlich ist, gibt es für eine mathematische Funktion immer nur einen Eingang und nur einen Ausgang. Dies gilt auch für funktionale Programmiersprachen, obwohl dies bei der ersten Verwendung möglicherweise nicht offensichtlich ist.
Dies scheint eine große Unannehmlichkeit zu sein. Wie kann ich etwas Nützliches ohne Funktionen mit zwei (oder mehr) Parametern tun?
Es stellt sich heraus, dass es einen Weg gibt, dies zu tun, und außerdem ist es auf F # vollständig transparent. Es heißt "Currying" und verdient einen separaten Beitrag, der in naher Zukunft erscheinen wird.
Tatsächlich wird später klar, dass diese beiden „nutzlosen“ Eigenschaften unglaublich wertvoll werden und der Schlüssel sein werden, der die funktionale Programmierung so leistungsfähig macht.
Zusätzliche Ressourcen
Es gibt viele Tutorials für F #, einschließlich Materialien für diejenigen, die mit C # oder Java-Erfahrung kommen. Die folgenden Links können hilfreich sein, wenn Sie tiefer in F # einsteigen:
Es werden auch verschiedene andere Möglichkeiten beschrieben , um mit dem Lernen von F # zu beginnen .
Schließlich ist die F # Community sehr anfängerfreundlich. Bei Slack gibt es einen sehr aktiven Chat, der von der F # Software Foundation unterstützt wird, mit Anfängerräumen, an denen Sie frei teilnehmen können . Wir empfehlen Ihnen dringend, dies zu tun!
Vergessen Sie nicht, die Seite der russischsprachigen Community F # zu besuchen! Wenn Sie Fragen zum Erlernen einer Sprache haben, diskutieren wir diese gerne in Chatrooms:
Über Übersetzungsautoren
Übersetzt von @kleidemos
 Übersetzungs- und redaktionelle Änderungen wurden durch die Bemühungen der russischsprachigen Community von F # -Entwicklern vorgenommen . Wir danken auch @schvepsss und @shwars für die Vorbereitung dieses Artikels zur Veröffentlichung.
Übersetzungs- und redaktionelle Änderungen wurden durch die Bemühungen der russischsprachigen Community von F # -Entwicklern vorgenommen . Wir danken auch @schvepsss und @shwars für die Vorbereitung dieses Artikels zur Veröffentlichung.