Normale Zuordnung

Alle Szenen, die wir verwenden, bestehen aus Polygonen, die wiederum aus Hunderten, Tausenden von absolut flachen Dreiecken bestehen. Wir haben es bereits geschafft, den Realismus der Szenen aufgrund zusätzlicher Details, die die Anwendung zweidimensionaler Texturen auf diese flachen Dreiecke ermöglichen, leicht zu erhöhen. Durch die Texturierung wird die Tatsache verborgen, dass alle Objekte in der Szene nur eine Sammlung vieler kleiner Dreiecke sind. Eine großartige Technik, aber ihre Möglichkeiten sind nicht unbegrenzt: Wenn man sich einer Oberfläche nähert, wird einem klar, dass sie aus flachen Oberflächen besteht. Die meisten realen Objekte sind nicht vollständig flach und weisen viele Reliefdetails auf.


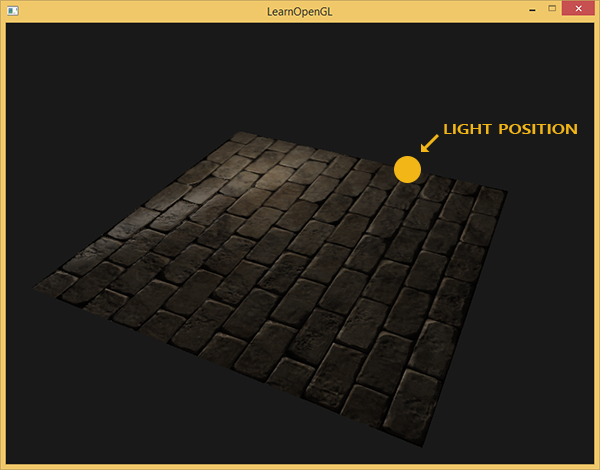
Nehmen Sie zum Beispiel Mauerwerk. Seine Oberfläche ist sehr rau und wird offensichtlich nicht durch eine Ebene dargestellt: Auf ihm befinden sich Aussparungen mit Zement und viele kleine Details wie Löcher und Risse. Wenn wir eine Szene mit Nachahmung von Mauerwerk in Gegenwart von Licht analysieren, wird die Illusion eines Oberflächenreliefs sehr leicht zerstört. Das Folgende ist ein Beispiel für eine solche Szene, die eine Ebene mit einer Mauerwerkstruktur und einer Punktlichtquelle enthält:


Wie Sie sehen, berücksichtigt die Beleuchtung die für diese Oberfläche angenommenen Reliefdetails überhaupt nicht: Alle kleinen Risse und Hohlräume mit Zement sind vom Rest der Oberfläche nicht zu unterscheiden. Man könnte eine spiegelnde Glanzkarte verwenden, um die Beleuchtung bestimmter Details zu begrenzen, die sich in den Aussparungen der Oberfläche befinden. Dies sieht jedoch eher nach einem schmutzigen Hack als nach einer funktionierenden Lösung aus. Was wir brauchen, ist eine Möglichkeit, die Beleuchtungsgleichungen mit Daten auf dem Oberflächenmikrorelief zu versorgen.
Betrachten Sie im Zusammenhang mit den uns bekannten Beleuchtungsgleichungen folgende Frage: Unter welchen Bedingungen wird die Oberfläche als vollkommen flach beleuchtet? Die Antwort bezieht sich auf die Normale zur Oberfläche. Aus Sicht des Beleuchtungsalgorithmus werden Informationen über die Oberflächenform nur über den Normalenvektor übertragen. Da der Normalenvektor überall auf der oben dargestellten Oberfläche konstant ist, ist auch die Beleuchtung entsprechend der Ebene gleichmäßig. Was aber, wenn wir an den Beleuchtungsalgorithmus nicht die einzige normale Konstante für alle zum Objekt gehörenden Fragmente übergeben, sondern die normale eindeutige Konstante für jedes Fragment? Somit ändert sich der Normalenvektor basierend auf der Oberflächentopographie geringfügig, wodurch eine überzeugendere Illusion der Oberflächenkomplexität erzeugt wird:


Durch die Verwendung fragmentarisch unterschiedlicher Normalen betrachtet der Beleuchtungsalgorithmus die Oberfläche als aus vielen mikroskopischen Ebenen senkrecht zu ihrem Normalenvektor zusammengesetzt. Infolgedessen wird dem Objekt eine erhebliche Textur hinzugefügt. Die Technik zum Anwenden von Normalen, die nur für ein Fragment und nicht für die gesamte Oberfläche gelten - dies ist Normal Mapping oder Bump Mapping . Wie auf eine bereits bekannte Szene angewendet:


Sie können die beeindruckende Zunahme der visuellen Komplexität aufgrund der sehr geringen Leistungskosten sehen. Da wir alle Änderungen im Beleuchtungsmodell nur in der Bereitstellung einer eindeutigen Normalen in jedem Fragment sind, werden keine Berechnungsformeln geändert. Nur am Eingang kommt anstelle der interpolierten Normalen die Normalen für das aktuelle Fragment an die Oberfläche. Dieselben Beleuchtungsgleichungen erledigen den Rest der Arbeit, um die Illusion von Erleichterung zu erzeugen.

Normale Zuordnung

Es stellt sich also heraus, dass wir den Beleuchtungsalgorithmus mit Normalen versehen müssen, die für jedes Fragment eindeutig sind. Wir werden die Methode verwenden, die bereits in diffusen und spiegelnden Reflexionstexturen bekannt ist, und die übliche 2D-Textur verwenden, um normale Daten an jedem Punkt auf der Oberfläche zu speichern. Seien Sie nicht überrascht, Texturen eignen sich auch hervorragend zum Speichern normaler Vektoren. Dann müssen wir nur noch aus der Textur auswählen, den normalen Vektor wiederherstellen und Beleuchtungsberechnungen durchführen.

Auf den ersten Blick ist möglicherweise nicht klar, wie Vektordaten in einer regulären Textur gespeichert werden sollen, die normalerweise zum Speichern von Farbinformationen verwendet wird. Aber denken Sie eine Sekunde darüber nach: Die RGB-Farbtriade ist im Wesentlichen ein dreidimensionaler Vektor. Auf ähnliche Weise können Sie die Komponenten des XYZ-Normalenvektors in den entsprechenden Farbkomponenten speichern. Die Werte der Komponenten des Normalenvektors liegen im Intervall [-1, 1] und erfordern daher eine zusätzliche Umrechnung in das Intervall [0, 1]:

vec3 rgb_normal = normal * 0.5 + 0.5; //   [-1,1]  [0,1] 

Eine solche Reduzierung des Normalenvektors auf den Raum der RGB-Farbkomponenten ermöglicht es uns, den Normalenvektor in der Textur zu speichern, der auf der Grundlage des tatsächlichen Reliefs des modellierten Objekts erhalten wird und für jedes Fragment eindeutig ist. Ein Beispiel für eine solche Textur - normale Karten - für dasselbe Mauerwerk:


Es ist interessant, den blauen Farbton dieser normalen Karte zu beachten (fast alle normalen Karten haben einen ähnlichen Farbton). Dies geschieht, weil alle Normalen ungefähr entlang der oZ-Achse ausgerichtet sind, die durch das Koordinaten-Tripel (0, 0, 1) dargestellt wird, d.h. in Form einer Farbtriade - reines Blau. Kleine Änderungen des Farbtons sind eine Folge der Abweichung der Normalen von der positiven Halbachse oZ in einigen Bereichen, was unebenem Gelände entspricht. Sie können also sehen, dass die Textur an den oberen Rändern jedes Ziegels einen grünen Farbton annimmt. Und das ist logisch: Auf den oberen Seiten des Ziegels sollten die Normalen mehr auf die oY-Achse (0, 1, 0) ausgerichtet sein, die Grün entspricht.

Nehmen Sie für die Testszene eine Ebene, die auf die positive Halbachse oZ ausgerichtet ist, und verwenden Sie dafür die folgende diffuse Karte und die normale Karte .

Bitte beachten Sie, dass die normale Karte auf dem Link und im Bild oben unterschiedlich ist. In dem Artikel erwähnte der Autor die Gründe für die Unterschiede eher beiläufig und beschränkte sich darauf, die zu konvertierenden normalen Karten so zu empfehlen, dass die grüne Komponente im System lokal auf der Texturebene eher "unten" als "oben" anzeigt.
Wenn Sie genauer hinschauen, wirken hier zwei Faktoren zusammen:

• Der Unterschied besteht darin, wie Texel im Client-Speicher und im OpenGL-Texturspeicher adressiert werden
• Das Vorhandensein von zwei Notationen für normale Karten. Herkömmlicherweise zwei Camps: DirectX-Stil und OpenGL-Stil

In Bezug auf normale Kartennotationen sind historisch gesehen zwei Lager bekannt: DirectX und OpenGL.

Anscheinend sind sie nicht kompatibel. Und mit ein wenig Nachdenken können Sie verstehen, dass DirectX den Tangentenraum als Linkshänder und OpenGL als Rechtshänder betrachtet. Wenn Sie die normale X-Karte unserer Anwendung ohne Änderungen verschieben, führt dies zu einer falschen Beleuchtung, und es ist nicht immer sofort klar, dass sie falsch ist. Insbesondere werden die Ausbuchtungen im OpenGL-Format zu Einkerbungen für DirectX und umgekehrt.
Für die Adressierung: Laden von Daten aus einer Texturdatei in den Speicher wird angenommen, dass das erste Texel das obere linke Texel des Bildes ist. Um Texturdaten im Anwendungsspeicher darzustellen, gilt dies im Allgemeinen. OpenGL verwendet jedoch ein anderes Texturkoordinatensystem: Das erste Texel befindet sich unten links. Für eine korrekte Texturierung werden Bilder normalerweise im Code des einen oder anderen Bilddatei-Laders entlang der Y-Achse gespiegelt. Für Stb_image, das im Unterricht verwendet wird, müssen Sie ein Kontrollkästchen hinzufügen

 stbi_set_flip_vertically_on_load(1); 

Das Lustige ist, dass zwei Optionen in Bezug auf die Beleuchtung korrekt angezeigt werden: eine normale Karte in OpenGL-Notation mit aktivierter Y-Reflexion oder eine normale Karte in DirectX-Notation mit deaktivierter Y-Reflexion. Die Beleuchtung funktioniert in beiden Fällen korrekt, der Unterschied bleibt nur in der Umkehrung der Textur entlang der Achse Y. Y.

Hinweis trans.

Laden Sie also beide Texturen, binden Sie sie an die Texturblöcke und rendern Sie die vorbereitete Ebene unter Berücksichtigung der folgenden Änderungen des Fragment-Shader-Codes:

 uniform sampler2D normalMap; void main() { //         [0,1] normal = texture(normalMap, fs_in.TexCoords).rgb; //      [-1,1] normal = normalize(normal * 2.0 - 1.0); [...] //  ... } 

Hier wenden wir die inverse Transformation vom RGB-Werteraum auf einen vollständigen Normalenvektor an und verwenden sie dann einfach im bekannten Blinn-Fong-Beleuchtungsmodell.

Wenn Sie nun langsam die Position der Lichtquelle in der Szene ändern, können Sie die Illusion des Oberflächenreliefs spüren, das die normale Karte bietet:


Es bleibt jedoch ein Problem, das den Bereich der möglichen Verwendung normaler Karten drastisch einschränkt. Wie bereits erwähnt, deutete der blaue Farbton der normalen Karte darauf hin, dass alle Vektoren in der Textur im Durchschnitt entlang der positiven Achse oZ ausgerichtet sind. In unserer Szene verursachte dies keine Probleme, da die Normale zur Oberfläche der Ebene ebenfalls mit oZ ausgerichtet war. Was passiert jedoch, wenn wir die Position der Ebene in der Szene so ändern, dass die Normale dazu mit der positiven Achse oY ausgerichtet ist?


Die Beleuchtung erwies sich als völlig falsch! Und der Grund ist einfach: Die Normalen aus der Karte geben immer noch Vektoren zurück, die entlang der positiven Halbachse oZ ausgerichtet sind, obwohl sie in diesem Fall in Richtung der positiven Halbachse oY der Oberflächennormalen ausgerichtet sein sollten. Gleichzeitig erfolgt die Berechnung der Beleuchtung so, als ob sich die Normalen zur Oberfläche befinden, als ob die Ebene immer noch auf die positive Halbachse oZ ausgerichtet ist, was zu einem falschen Ergebnis führt. Die folgende Abbildung zeigt deutlicher die Ausrichtung der aus der Karte abgelesenen Normalen relativ zur Oberfläche:


Es ist ersichtlich, dass die Normalen im Allgemeinen entlang der positiven Halbachse oZ ausgerichtet sind, obwohl sie entlang der Normalen zu der Oberfläche ausgerichtet sein sollten, die entlang der positiven Halbachse oY gerichtet ist.
Eine mögliche Lösung wäre, für jede Ausrichtung der betrachteten Oberfläche eine separate Normalkarte zu erstellen. Für einen Würfel wären sechs normale Karten erforderlich, aber für komplexere Modelle ist die Anzahl der möglichen Ausrichtungen möglicherweise zu hoch und für die Implementierung nicht geeignet.

Es gibt einen anderen, mathematisch komplizierteren Ansatz, der die Berechnung der Beleuchtung in einem anderen Koordinatensystem bietet: so dass die darin enthaltenen Normalenvektoren immer ungefähr mit der positiven Halbachse oZ übereinstimmen. Andere für Beleuchtungsberechnungen erforderliche Vektoren werden dann in dieses Koordinatensystem konvertiert. Diese Methode ermöglicht es, eine normale Karte für jede Ausrichtung des Objekts zu verwenden. Und dieses spezifische Koordinatensystem wird Tangentenraum oder Tangentenraum genannt .

Tangentenraum

Es sollte beachtet werden, dass der Normalenvektor in der Normalkarte direkt im Tangentenraum ausgedrückt wird, d.h. in einem solchen Koordinatensystem, dass die Normale immer ungefähr in Richtung der positiven Halbachse oZ gerichtet ist. Der Tangentenraum ist als ein Koordinatensystem definiert, das lokal in der Ebene des Dreiecks liegt, und jeder Normalenvektor ist innerhalb dieses Koordinatensystems definiert. Sie können sich dieses System als lokales Koordinatensystem für eine normale Karte vorstellen: Alle darin enthaltenen Vektoren sind unabhängig von der endgültigen Ausrichtung der Oberfläche auf die positive Halbachse oZ gerichtet. Mit speziell vorbereiteten Transformationsmatrizen ist es möglich, Normalenvektoren aus diesem lokalen Tangentenkoordinatensystem in Welt- oder Ansichtskoordinaten zu transformieren und diese entsprechend der endgültigen Position der strukturierten Oberflächen auszurichten.
Betrachten Sie das vorherige Beispiel mit der falschen Verwendung der normalen Abbildung, bei der die Ebene entlang der positiven Achse oY ausgerichtet war. Da die Normalenkarte im Tangentenraum definiert ist, besteht eine der Anpassungsoptionen darin, die Matrix der Normalenübergänge vom Tangentenraum in einen solchen zu berechnen, dass sie normal zur Oberfläche ausgerichtet werden. Dies würde dazu führen, dass die Normalen entlang der positiven Achse oY ausgerichtet werden. Eine bemerkenswerte Eigenschaft des Tangentenraums ist die Tatsache, dass wir durch Berechnung einer solchen Matrix die Normalen auf jede Oberfläche und ihre Ausrichtung neu ausrichten können.

Eine solche Matrix wird als TBN abgekürzt, was eine Abkürzung für den Namen des Tripel der Vektoren Tangente , Bitangente und Normal ist . Wir müssen diese drei Vektoren finden, um diese Basisänderungsmatrix zu bilden. Eine solche Matrix macht den Übergang eines Vektors vom Tangentenraum zu einem anderen und für seine Bildung sind drei zueinander senkrechte Vektoren erforderlich, deren Ausrichtung der Ausrichtung der normalen Kartenebene entspricht. Dies ist ein Richtungsvektor nach oben, rechts und vorne, ein Satz, der uns aus der Lektion über die virtuelle Kamera bekannt ist .
Mit dem oberen Vektor ist sofort alles klar - dies ist unser normaler Vektor. Der rechte und der Vorwärtsvektor werden als Tangente bzw. Bitangens bezeichnet. Die folgende Abbildung gibt eine Vorstellung von ihrer relativen Position in der Ebene:


Die Berechnung der Tangente und der Bi-Tangente ist nicht so offensichtlich wie die Berechnung des Normalenvektors. In der Abbildung sehen Sie, dass die Richtungen der Tangente und die Tangentenkarte der Normalen an den Achsen ausgerichtet sind, die die Texturkoordinaten der Oberfläche angeben. Diese Tatsache ist die Grundlage für die Berechnung dieser beiden Vektoren, was einige mathematische Kenntnisse erfordert. Schauen Sie sich das Bild an:


Änderungen der Texturkoordinaten entlang der Kante eines Dreiecks $$$E_2$bezeichnet als $$$\ Delta U_2$und $$$\ Delta V_2$ausgedrückt in den gleichen Richtungen wie die Tangentenvektoren $$$T$und bi-tangential $$$B$. Basierend auf dieser Tatsache können Sie die Kanten eines Dreiecks ausdrücken $$$E_1$und $$$E_2$in Form einer linearen Kombination von Tangenten- und Bi-Tangentenvektoren:

$$

$$E_1 = \ Delta U_1T + \ Delta V_1B$$

$$

$$E_2 = \ Delta U_2T + \ Delta V_2B$$

Wenn wir uns in eine bitweise Aufzeichnung verwandeln, erhalten wir:

$$

$$(E_ {1x}, E_ {1y}, E_ {1z}) = \ Delta U_1 (T_x, T_y, T_z) + \ Delta V_1 (B_x, B_y, B_z)$$

$$

$$(E_ {2x}, E_ {2y}, E_ {2z}) = \ Delta U_2 (T_x, T_y, T_z) + \ Delta V_2 (B_x, B_y, B_z)$$

$$$E$wird als Vektor der Differenz zweier Vektoren berechnet und $$$\ Delta U$und $$$\ Delta V$als Unterschied in den Texturkoordinaten. Es bleiben zwei Unbekannte in zwei Gleichungen zu finden: die Tangente $$$T$und Voreingenommenheit $$$B$. Wenn Sie sich an die Lehren der Algebra erinnern, wissen Sie, dass solche Bedingungen es ermöglichen, das System für zu lösen $$$T$und für $$$B$.
Die letzte gegebene Form von Gleichungen erlaubt es uns, sie in Form einer Matrixmultiplikation umzuschreiben:

$$

$$\ begin {bmatrix} E_ {1x} & E_ {1y} & E_ {1z} \\ E_ {2x} & E_ {2y} & E_ {2z} \ end {bmatrix} = \ begin {bmatrix} \ Delta U_1 & \ Delta V_1 \\ \ Delta U_2 & \ Delta V_2 \ end {bmatrix} \ begin {bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \ end {bmatrix}$$

Versuchen Sie, die Matrixmultiplikation in Ihrem Kopf durchzuführen, um sicherzustellen, dass die Aufzeichnung korrekt ist. Das Schreiben eines Systems in Matrixform erleichtert das Verständnis des Ansatzes zum Finden erheblich $$$T$und $$$B$. Multiplizieren Sie beide Seiten der Gleichung mit der Umkehrung von $$$\ Delta U \ Delta V$::

$$

$$\ begin {bmatrix} \ Delta U_1 & \ Delta V_1 \\ \ Delta U_2 & \ Delta V_2 \ end {bmatrix} ^ {- 1} \ begin {bmatrix} E_ {1x} & E_ {1y} & E_ {1z } \\ E_ {2x} & E_ {2y} & E_ {2z} \ end {bmatrix} = \ begin {bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \ end {bmatrix}$$

Wir bekommen eine Entscheidung bezüglich $$$T$und $$$B$Dies erfordert jedoch die Berechnung der inversen Matrix von Änderungen der Texturkoordinaten. Wir werden nicht auf Details der Berechnung inverser Matrizen eingehen - der Ausdruck für die inverse Matrix sieht aus wie das Produkt der Zahl, die zur Determinante der ursprünglichen Matrix und der zugehörigen Matrix invers ist:

$$

$$\ begin {bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \ end {bmatrix} = \ frac {1} {\ Delta U_1 \ Delta V_2 - \ Delta U_2 \ Delta V_1} \ begin {bmatrix} \ Delta V_2 & - \ Delta V_1 \\ - \ Delta U_2 & \ Delta U_1 \ end {bmatrix} \ begin {bmatrix} E_ {1x} & E_ {1y} & E_ {1z} \\ E_ {2x} & E_ { 2y} & E_ {2z} \ end {bmatrix}$$

Dieser Ausdruck ist die Formel zur Berechnung des Tangentenvektors $$$T$und bi-tangential $$$B$basierend auf den Koordinaten der Flächen des Dreiecks und den entsprechenden Texturkoordinaten.
Machen Sie sich keine Sorgen, wenn Ihnen das Wesentliche der obigen mathematischen Berechnungen entgeht. Wenn Sie verstehen, dass wir die Tangente und die Bias-Tangente basierend auf den Koordinaten der Eckpunkte des Dreiecks und ihren Texturkoordinaten erhalten (da die Texturkoordinaten auch zum Tangentenraum gehören), ist dies bereits die halbe Miete.

Berechnung von Tangenten und Bitangens

Im Beispiel dieser Lektion haben wir eine einfache Ebene genommen, die in Richtung der positiven Halbachse oZ schaut. Jetzt werden wir versuchen, eine normale Abbildung mithilfe des Tangentenraums zu implementieren, um die Ebene im Beispiel nach Belieben ausrichten zu können, ohne den normalen Abbildungseffekt zu zerstören. Unter Verwendung der obigen Berechnung ermitteln wir manuell die Tangente und die Bi-Tangente an die betrachtete Oberfläche.
Wir nehmen an, dass die Ebene aus den folgenden Eckpunkten mit Texturkoordinaten besteht (zwei Dreiecke sind durch die Vektoren 1, 2, 3 und 1, 3, 4 gegeben):

 //   glm::vec3 pos1(-1.0, 1.0, 0.0); glm::vec3 pos2(-1.0, -1.0, 0.0); glm::vec3 pos3( 1.0, -1.0, 0.0); glm::vec3 pos4( 1.0, 1.0, 0.0); //   glm::vec2 uv1(0.0, 1.0); glm::vec2 uv2(0.0, 0.0); glm::vec2 uv3(1.0, 0.0); glm::vec2 uv4(1.0, 1.0); //   glm::vec3 nm(0.0, 0.0, 1.0); 

Zuerst berechnen wir die Vektoren, die die Flächen des Dreiecks beschreiben, sowie die Deltas der Texturkoordinaten:

 glm::vec3 edge1 = pos2 - pos1; glm::vec3 edge2 = pos3 - pos1; glm::vec2 deltaUV1 = uv2 - uv1; glm::vec2 deltaUV2 = uv3 - uv1; 

Mit den erforderlichen Anfangsdaten können wir beginnen, die Tangente und die Bi-Tangente direkt anhand der Formeln aus dem vorherigen Abschnitt zu berechnen:

 float f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y); tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x); tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y); tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z); tangent1 = glm::normalize(tangent1); bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x); bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y); bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z); bitangent1 = glm::normalize(bitangent1); [...] //         

Zuerst nehmen wir die Bruchkomponente des endgültigen Ausdrucks in einer separaten Variablen f heraus . Dann führen wir für jede Komponente der Vektoren den entsprechenden Teil der Matrixmultiplikation durch und multiplizieren mit f . Wenn Sie diesen Code mit der endgültigen Berechnungsformel vergleichen, sehen Sie, dass dies die wörtliche Anordnung ist. Vergessen Sie nicht, am Ende zu normalisieren, damit die gefundenen Vektoren Einheit sind.

Da das Dreieck eine flache Figur ist, reicht es aus, die Tangente und die Bi-Tangente einmal pro Dreieck zu berechnen - sie sind für alle Eckpunkte gleich. Es ist erwähnenswert, dass die meisten Implementierungen der Arbeit mit Modellen (wie Ladern oder Landschaftsgeneratoren) eine solche Organisation von Dreiecken verwenden, bei denen sie Eckpunkte mit anderen Dreiecken teilen. In solchen Fällen greifen Entwickler normalerweise auf Mittelungsparameter an gemeinsamen Eckpunkten zurück, z. B. normale Vektoren, Tangens und Bi-Tangens, um ein gleichmäßigeres Ergebnis zu erzielen. Die Dreiecke, aus denen unsere Ebene besteht, haben auch mehrere Eckpunkte gemeinsam. Da beide jedoch in derselben Ebene liegen, ist keine Mittelwertbildung erforderlich. Dennoch ist es nützlich, sich an das Vorhandensein eines solchen Ansatzes in realen Anwendungen und Aufgaben zu erinnern.

Die resultierenden Tangenten- und Bi-Tangentenvektoren müssen die Werte (1, 0, 0) bzw. (0, 1, 0) haben. Das bildet zusammen mit dem Normalenvektor (0, 0, 1) die orthogonale Matrix TBN. Wenn Sie die resultierende Basis mit der Ebene visualisieren, erhalten Sie das folgende Bild:


Nachdem Sie die Vektoren berechnet haben, können Sie mit der vollständigen Implementierung der normalen Zuordnung fortfahren.

Normale Abbildung im Tangentenraum

Zuerst müssen Sie eine TBN-Matrix in den Shadern erstellen. Zu diesem Zweck übertragen wir die vorbereiteten Tangenten- und Bi-Tangentenvektoren über die Scheitelpunktattribute auf den Scheitelpunkt-Shader:

 #version 330 core layout (location = 0) in vec3 aPos; layout (location = 1) in vec3 aNormal; layout (location = 2) in vec2 aTexCoords; layout (location = 3) in vec3 aTangent; layout (location = 4) in vec3 aBitangent; 

Im Vertex-Shader-Code selbst bilden wir die Matrix direkt:

 void main() { [...] vec3 T = normalize(vec3(model * vec4(aTangent, 0.0))); vec3 B = normalize(vec3(model * vec4(aBitangent, 0.0))); vec3 N = normalize(vec3(model * vec4(aNormal, 0.0))); mat3 TBN = mat3(T, B, N) } 

Im obigen Code konvertieren wir zuerst alle Vektoren der Basis des Tangentenraums in ein Koordinatensystem, in dem wir gut arbeiten können - in diesem Fall ist dies das Weltkoordinatensystem und wir multiplizieren die Vektoren mit dem Modellmatrixmodell . Als nächstes erstellen wir die TBN-Matrix selbst, indem wir einfach alle drei entsprechenden Vektoren an einen Konstruktor vom Typ mat3 übergeben . Bitte beachten Sie, dass es für die Richtigkeit der Berechnungsreihenfolge erforderlich ist, die Vektoren nicht mit der Modellmatrix, sondern mit der Normalmatrix zu multiplizieren, da wir nur an der Ausrichtung der Vektoren interessiert sind, nicht jedoch an ihrer Verschiebung oder Skalierung

Genau genommen ist es nicht erforderlich, den Bi-Tangenten-Vektor auf den Shader zu übertragen.
Da das Tripel der TBN-Vektoren senkrecht zueinander steht, kann die Bi-Tangente durch Vektormultiplikation im Shader gefunden werden:

  vec3 B = cross(N, T) 

Die TBN-Matrix wird also empfangen. Wie verwenden wir sie? Tatsächlich gibt es zwei Ansätze für die Verwendung bei der normalen Zuordnung:

1. Verwenden Sie die TBN-Matrix, um alle erforderlichen Vektoren von der Tangente in den Weltraum zu transformieren. Übertragen Sie die Ergebnisse an den Fragment-Shader, wo Sie mithilfe der Matrix den Vektor von der normalen Karte in den Weltraum transformieren. Infolgedessen befindet sich der Normalvektor in dem Raum, in dem die gesamte Beleuchtung berechnet wird.
2. Nehmen Sie die inverse Matrix zu TBN und konvertieren Sie alle notwendigen Vektoren vom Weltraum in die Tangente. Das heißt, Verwenden Sie diese Matrix, um die an Beleuchtungsberechnungen beteiligten Vektoren in einen Tangentenraum umzuwandeln. Der Normalenvektor bleibt auch in diesem Fall im selben Raum wie die anderen Teilnehmer an der Berechnung der Beleuchtung.

Schauen wir uns die erste Option an. Der Normalenvektor aus der entsprechenden Textur wird im Tangentenraum angegeben, während die anderen bei der Berechnung der Beleuchtung verwendeten Vektoren im Weltraum definiert werden. Indem wir die TBN-Matrix an den Fragment-Shader übergeben, können wir den Normalenvektor transformieren, der durch Abtasten der Textur vom Tangentenraum zur Welt erhalten wird, wodurch die Einheit der Koordinatensysteme für alle Elemente der Beleuchtungsberechnung sichergestellt wird. In diesem Fall sind alle Berechnungen (insbesondere Skalarvektormultiplikationen) korrekt.

Die Übertragung der TBN-Matrix erfolgt auf einfachste Weise:

 out VS_OUT { vec3 FragPos; vec2 TexCoords; mat3 TBN; } vs_out; void main() { [...] vs_out.TBN = mat3(T, B, N); } 

Im Fragment-Shader-Code setzen wir jeweils eine Eingabevariable vom Typ mat3:

 in VS_OUT { vec3 FragPos; vec2 TexCoords; mat3 TBN; } fs_in; 

Wenn Sie die Matrix zur Hand haben, können Sie den Code zum Erhalten der Normalen durch den Ausdruck der Übersetzung von der Tangente in den Weltraum angeben:

 normal = texture(normalMap, fs_in.TexCoords).rgb; normal = normalize(normal * 2.0 - 1.0); normal = normalize(fs_in.TBN * normal); 

Da die resultierende Normalität jetzt im Weltraum festgelegt ist, müssen Sie im Shader-Code nichts anderes ändern. Beleuchtungsberechnungen, und nehmen daher einen normalen Vektor an, der in Weltkoordinaten angegeben ist.

Schauen wir uns auch den zweiten Ansatz an.Dazu muss die inverse TBN-Matrix erhalten und alle an der Beleuchtungsberechnung beteiligten Vektoren vom Weltkoordinatensystem auf den Vektor übertragen werden, der den aus der Textur erhaltenen Normalenvektoren entspricht - der Tangente. In diesem Fall bleibt die Bildung der TBN-Matrix unverändert, aber bevor wir zum Fragment-Shader übergehen, müssen wir die inverse Matrix erhalten:

 vs_out.TBN = transpose(mat3(T, B, N)); 

Beachten Sie, dass die Funktion transpose () anstelle von inverse () verwendet wird . Eine solche Substitution ist wahr, da für orthogonale Matrizen (bei denen alle Achsen durch zueinander senkrechte Einheitsvektoren dargestellt werden) das Erhalten der inversen Matrix ein Ergebnis ergibt, das mit der Transposition identisch ist. Dies ist sehr nützlich, da das Berechnen der inversen Matrix im allgemeinen Fall eine viel rechenintensivere Aufgabe ist als das Transponieren.

Im Fragment-Shader-Code konvertieren wir nicht den normalen Vektor, sondern andere wichtige Vektoren aus dem Weltkoordinatensystem in die Tangente, nämlich lightDir und viewDir. Diese Lösung bringt auch alle Elemente der Berechnungen in ein einziges Koordinatensystem, diesmal die Tangente.

 void main() { vec3 normal = texture(normalMap, fs_in.TexCoords).rgb; normal = normalize(normal * 2.0 - 1.0); vec3 lightDir = fs_in.TBN * normalize(lightPos - fs_in.FragPos); vec3 viewDir = fs_in.TBN * normalize(viewPos - fs_in.FragPos); [...] } 

Der zweite Ansatz scheint zeitaufwändiger zu sein und erfordert mehr Matrixmultiplikationen im Fragment-Shader (was die Leistung stark beeinträchtigt). Warum haben wir überhaupt angefangen, es zu zerlegen?
Tatsache ist, dass die Übersetzung von Vektoren von Weltkoordinaten in Tangenten einen zusätzlichen Vorteil bietet: Tatsächlich können wir den gesamten Transformationscode vom Fragment zum Vertex-Shader verschieben! Dieser Ansatz funktioniert, da sich lightPos und viewPos nicht von Fragment zu Fragment ändern und der Wert fs_in.FragPos lautetWir können auch in den Tangentenraum im Vertex-Shader übersetzen. Der interpolierte Wert am Eingang zum Fragment-Shader ist ziemlich korrekt. Für den zweiten Ansatz ist es daher nicht erforderlich, alle diese Vektoren in den Tangentenraum im Fragment-Shader-Code zu übersetzen, während der erste dies erfordert - die Normalen sind für jedes Fragment eindeutig.

Infolgedessen entfernen wir uns von der Übertragung der Matrix invers zu TBN auf den Fragment-Shader und übergeben ihm stattdessen den Positionsvektor des Scheitelpunkts, der Lichtquelle und des Beobachters im Tangentenraum. So werden wir die kostspieligen Matrixmultiplikationen im Fragment-Shader los, was eine signifikante Optimierung darstellt, da der Vertex-Shader viel seltener ausgeführt wird. Es ist dieser Vorteil, der den zweiten Ansatz in den meisten Fällen in die Kategorie der bevorzugten Verwendung einordnet.

 out VS_OUT { vec3 FragPos; vec2 TexCoords; vec3 TangentLightPos; vec3 TangentViewPos; vec3 TangentFragPos; } vs_out; uniform vec3 lightPos; uniform vec3 viewPos; [...] void main() { [...] mat3 TBN = transpose(mat3(T, B, N)); vs_out.TangentLightPos = TBN * lightPos; vs_out.TangentViewPos = TBN * viewPos; vs_out.TangentFragPos = TBN * vec3(model * vec4(aPos, 0.0)); 

Im Fragment-Shader wechseln wir zur Verwendung neuer Eingabevariablen bei Beleuchtungsberechnungen im Tangentenraum. Da die Normalen in diesem Raum bedingt definiert sind, bleiben alle Berechnungen korrekt.
Nachdem alle normalen Mapping-Berechnungen im Tangentenraum durchgeführt wurden, können wir die Ausrichtung der Testoberfläche in der Anwendung nach Belieben ändern und die Beleuchtung bleibt korrekt:

 glm::mat4 model(1.0f); model = glm::rotate(model, (float)glfwGetTime() * -10.0f, glm::normalize(glm::vec3(1.0, 0.0, 1.0))); shader.setMat4("model", model); RenderQuad(); 

Äußerlich sieht alles so aus, wie es sollte:


Quellen sind hier .

Komplexe Objekte

Wir haben also herausgefunden, wie man eine normale Abbildung im Tangentenraum durchführt und wie man die Tangenten- und Bias-Tangentenvektoren dafür unabhängig berechnet. Glücklicherweise ist eine solche manuelle Berechnung nicht so oft eine Aufgabe: Zum größten Teil wird dieser Code von Entwicklern irgendwo im Darm des Modellladers implementiert. In unserem Fall gilt dies für den verwendeten Assimp-Lader .

Assimp bietet ein sehr nützliches Optionsflag beim Laden von Modellen: aiProcess_CalcTangentSpace . Wenn es an die Funktion ReadFile () übergeben wird, berechnet die Bibliothek selbst die glatten Tangenten- und Bi-Tangentenlinien für jeden der geladenen Scheitelpunkte - ein Prozess, der dem hier beschriebenen ähnlich ist.

 const aiScene *scene = importer.ReadFile( path, aiProcess_Triangulate | aiProcess_FlipUVs | aiProcess_CalcTangentSpace ); 

Danach können Sie direkt auf die berechneten Tangenten zugreifen:

 vector.x = mesh->mTangents[i].x; vector.y = mesh->mTangents[i].y; vector.z = mesh->mTangents[i].z; vertex.Tangent = vector; 

Sie müssen auch den Download-Code aktualisieren, um den Empfang normaler Karten für strukturierte Modelle zu berücksichtigen. Das Wavefront Object (.obj) -Format exportiert normale Karten so, dass das Assimp-Flag aiTextureType_NORMAL nicht sicherstellt, dass diese Karten korrekt geladen werden, während alles korrekt mit dem Flag aiTextureType_HEIGHT funktioniert . Daher lade ich persönlich normalerweise normale Karten folgendermaßen:

 vector<Texture> normalMaps = loadMaterialTextures(material, aiTextureType_HEIGHT, "texture_normal"); 

Natürlich ist dieser Ansatz möglicherweise nicht für andere Modellbeschreibungsformate und Dateitypen geeignet. Ich stelle auch fest, dass das Setzen des Flags aiProcess_CalcTangentSpace nicht immer funktioniert. Wir wissen, dass die Berechnung von Tangenten auf Texturkoordinaten basiert. Oft wenden Modellautoren jedoch verschiedene Tricks auf Texturkoordinaten an, wodurch die Berechnung von Tangenten unterbrochen wird. Daher wird häufig ein Spiegelbild von Texturkoordinaten für symmetrisch strukturierte Modelle verwendet. Wenn die Tatsache der Spiegelung nicht berücksichtigt wird, ist die Berechnung der Tangenten falsch. Assimp führt diese Abrechnung nicht durch. Das hier bekannte Nanosuit-Modell eignet sich nicht zur Demonstration, da es auch Spiegelung verwendet.

Bei einem korrekt strukturierten Modell mit normalen und spiegelnden Karten liefert die Testanwendung ein sehr gutes Ergebnis:


Wie Sie sehen können, bietet die Verwendung der normalen Zuordnung eine spürbare Detailsteigerung und ist im Hinblick auf die Leistungskosten günstig.

Vergessen Sie nicht, dass die Verwendung der normalen Zuordnung dazu beitragen kann, die Leistung für eine bestimmte Szene zu verbessern. Ohne seine Verwendung ist das Erreichen von Modelldetails nur durch Erhöhen der Dichte des polygonalen Netzes möglich. Mit dieser Technik können Sie jedoch visuell den gleichen Detaillierungsgrad für Low-Poly-Netze erzielen. Unten sehen Sie einen Vergleich dieser beiden Ansätze:


Der Detaillierungsgrad des High-Poly-Modells und des Low-Poly-Modells unter Verwendung der normalen Zuordnung ist praktisch nicht zu unterscheiden. Diese Technik ist daher eine großartige Möglichkeit, High-Poly-Modelle in der Szene durch vereinfachte Modelle zu ersetzen, bei denen die visuelle Qualität praktisch nicht beeinträchtigt wird.

Letzter Kommentar

Es gibt ein weiteres technisches Detail bezüglich des normalen Mappings, das die Qualität mit geringen oder keinen zusätzlichen Kosten ein wenig verbessert.

In Fällen, in denen Tangenten für große und komplexe Netze mit einer signifikanten Anzahl von Eckpunkten berechnet werden, die zu mehreren Dreiecken gehören, werden die Tangentenvektoren normalerweise gemittelt, um ein glattes und visuell schönes normales Abbildungsergebnis zu erhalten. Dies schafft jedoch ein Problem: Nach der Mittelung kann das Dreifache der TBN-Vektoren die gegenseitige Rechtwinkligkeit verlieren, was auch den Verlust der Orthogonalität für die TBN-Matrix bedeutet. Im allgemeinen Fall ist das Ergebnis einer normalen Abbildung, die auf der Grundlage einer nicht orthogonalen Matrix erhalten wurde, nur geringfügig falsch, aber wir können es noch verbessern.

Dazu reicht es aus, eine einfache mathematische Methode anzuwenden:Gram-Schmidt-Prozess oder Reorthogonalisierung unserer dreifachen TBN-Vektoren. Im Vertex-Shader-Code:

 vec3 T = normalize(vec3(model * vec4(aTangent, 0.0))); vec3 N = normalize(vec3(model * vec4(aNormal, 0.0))); // - T  N T = normalize(T - dot(T, N) * N); //    B    T  N vec3 B = cross(N, T); mat3 TBN = mat3(T, B, N) 

Diese, wenn auch geringfügige Änderung verbessert die Qualität der normalen Zuordnung im Austausch gegen geringe Gemeinkosten. Wenn Sie an den Details dieses Verfahrens interessiert sind, können Sie sich den letzten Teil des Videos "Normal Mapping Mathematics" ansehen, dessen Link unten angegeben ist.

Zusätzliche Ressourcen

• Tutorial 26: Normales Mapping : Eine Lektion über normales Mapping von ogldev .
• Funktionsweise von Normal Mapping : Ein Video-Tutorial, in dem die Grundlagen von Normal Mapping von TheBennyBox erläutert werden .
• Normal Mapping Mathematics : Ein Film, der mit dem vorherigen verwandt ist und die Mathematik erklärt, die in der Normal Mapping-Methode verwendet wird, ebenfalls von TheBennyBox .
• Tutorial 13: Normales Mapping : Eine weitere Lektion von opengl-tutorial.org .

PS : Wir haben ein Telegramm Conf für die Koordination der Überweisungen. Wenn Sie ernsthaft bei der Übersetzung helfen möchten, sind Sie herzlich willkommen!