Die Dynamik des Vertikalfluges eines Flugzeugs ist leichter als Luft

Einführung

Die Bestimmung der Auf- und Abstiegsgeschwindigkeit von Flugzeugen, die bisher leichter als Luft (LALV) sind, ist fast eine wichtige Aufgabe, die sich bei der Konstruktion solcher Geräte ergibt.

Eine große Anzahl von Veröffentlichungen widmet sich beispielsweise LALF. Nur auf unserer Ressource befinden sich zwei sehr interessante Artikel [1,2] zur Entwicklungsgeschichte am Beispiel spezifischer Konstruktionen von Luftschiffen und Stratostaten. Es gibt jedoch nur sehr wenige Berechnungen der Dynamik des Vertikalfluges solcher Geräte, die es ermöglichen, die Auf- und Abstiegsgeschwindigkeit des SALW zumindest grob zu bestimmen.

Die letzte Aussage bedarf einer gewissen Erklärung, da sich ein erfahrener Leser an den Schulphysikkurs erinnert, in dem Probleme mit der Höhe des Anstiegs und anderen Parametern von Ballons, die mit Gasen gefüllt sind, die leichter als Luft sind, oder durch die Luft selbst, die während des Fluges erwärmt wurde, gelöst wurden.

Alle diese Aufgaben beruhten auf der Gleichheit zweier Kräfte: der Gewichtskraft und der Auftriebskraft. Gase wurden als ideal angesehen und ihre Parameter wurden nach dem Gesetz von Mendeleev Clapeyron berechnet. Selbst eine einfache Berechnung der dritten Kraft des Luftwiderstands führt jedoch bereits zu einem System von Differentialgleichungen, das nicht analytisch gelöst werden kann. Es ist auch notwendig, die Änderung der Dichte der atmosphärischen Luft mit der Höhe des Anstiegs und der Temperatur zu berücksichtigen.

Wenn Sie nicht nur den Aufstieg, sondern auch das Einfrieren des Balls und seinen Abstieg zum Boden berücksichtigen müssen, ist dies überhaupt keine Kinderaufgabe. Ich hoffe, dass die Berücksichtigung der Lösung eines ähnlichen Problems mittels Python nicht nur zur Erweiterung des Wissens in der Physik beiträgt, sondern auch zur Popularisierung der Programmiersprache Python selbst. Was ich in meinen Veröffentlichungen zu dieser Ressource zu tun versuche.

Ein mathematisches Modell des Fluges eines LALV mit einer Kugelschale, deren Volumen sich mit der Höhe nicht ändert

Wir beschränken uns darauf, die Bewegung seines Massenschwerpunkts unter Einwirkung der folgenden Kräfte zu betrachten: Schwerkraft ( G ), archimedische Kraft ( Fa ) und aerodynamische Widerstandskraft ( Fc ). Wir schreiben die Beziehungen zur Bestimmung der Kräfte durch die Parameter Bewegung und Luftumgebung [3]:





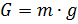
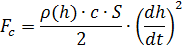
In den obigen Formeln wird die Notation verwendet: h ist die Höhe des Balls, dh / dt ist die vertikale Geschwindigkeit, m ist die Masse, g ist die Beschleunigung der Schwerkraft, W ist das Volumen des Balls, c ist der Luftwiderstandsbeiwert, S ist der charakteristische Widerstandsbereich (Mittelschiffbereich).
Die Abhängigkeit der Luftdichte von der Höhe wird als exponentiell angenommen:



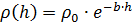
wo $$$ρ_0$- Luftdichte in Nullhöhe, b - Koeffizient. Die Schwerkraft ist nach unten gerichtet, die archimedische Kraft ist nach oben gerichtet, und die Kraft des Luftwiderstands ist immer "gegen die Bewegung" gerichtet. Daher erfordert die korrekte Einbeziehung dieser Kraft in die Bewegungsgleichungen die Einführung eines Faktors $$$-sing (dh / dt)$.

Für unsere Zwecke ist diese Tatsache jedoch nicht von grundlegender Bedeutung, und wir beschränken uns darauf, nur das Stadium des Anhebens des Balls zu betrachten, wenn die Kraft des Luftwiderstands nach unten gerichtet ist und daher in den Bewegungsgleichungen mit einem Minuszeichen berücksichtigt wird. Nun kann die Bewegungsgleichung wie folgt geschrieben werden:

, (1)

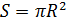
Angenommen, der Ballon ist ein homogener Körper mit dem Radius R und der Dichte $$$ρ_b$. Dann wird die Größe des Bereichs definiert, der seinen Luftwiderstand bestimmt Volumen als bzw. Masse als .

Nun ist klar, dass jeder Term von Gleichung (1) S. als Faktor enthält. Daher kann jeder Term der Bewegungsgleichung um einen Faktor von S reduziert werden. Die Gleichung selbst hat die Form:

, (2)

Wir führen die folgende Notation ein:

;;
;;

und schreibe (2) in Form des folgenden Systems nichtlinearer Gleichungen um:

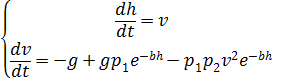
, (3)

Einfluss auf die Geschwindigkeit und Höhe des Anstiegs der LALV-Lufttemperatur

Dazu lösen wir zunächst das System (3) unter Verwendung der folgenden Beziehung für die Abhängigkeit der Dichte der atmosphärischen Luft von der Höhe ohne Berücksichtigung der Temperatur:



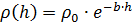
Wiederholen wir die Lösung von System (3), aber verwenden wir die Beziehung für die Abhängigkeit der Luftdichte von Höhe und Temperatur:



wobei: b = 0,000125 eine Konstante ist, die mit einer Luftdichte von 1 / m verbunden ist;
a = 0,0065 ist eine Konstante in Bezug auf die Lufttemperatur in K / m.
$$$T_0 = 300 K$- Temperatur auf Meereshöhe.


Wir bekommen:



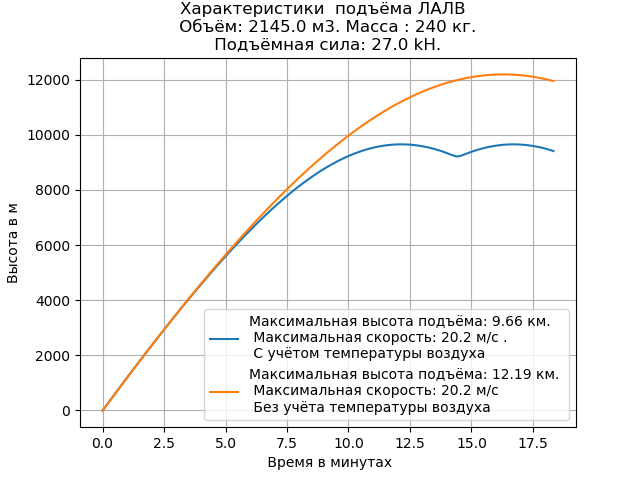
Der berechnete Wert der Höhe des LALV-Lifts unter Berücksichtigung der Temperatur ist geringer als ohne Berücksichtigung. Die Hubgeschwindigkeit der Vorrichtung bleibt unverändert.

Bestimmung der Eigenschaften aller Phasen des SALV-Fluges vom Start bis zur Landung

Um das Flugprogramm LALV zu erstellen, berücksichtigen Sie die Bedingungen für die folgenden Zeiträume:

Aufstieg - ;;
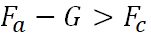
Hang - ;;
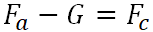
Landung - .


Wir bekommen:



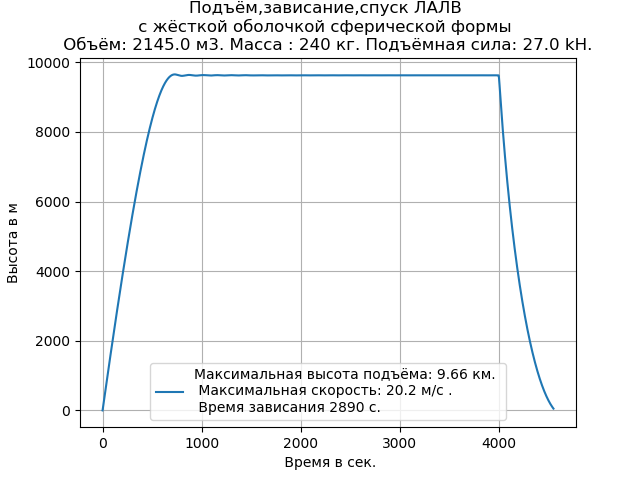
Wie aus der Grafik und der Auflistung des Programms hervorgeht, reicht es zur Durchführung eines Computerexperiments aus, die erforderlichen Anfangsdaten einzugeben.

Ein mathematisches Modell des Fluges eines LALV mit einer Schale, deren Volumen mit der Höhe variiert

Solche LALV umfassen Stratostaten. Der stratosphärische Ballon kann nicht vollständig mit Helium aufgeblasen werden, was ihm eine maximale Auftriebskraft verleiht, die die Form seiner Schale in eine Kugel verwandelt. Ein solcher Ball in großer Höhe kann aufgrund des erhöhten Unterschieds im Innen- und Außendruck platzen.

Aus diesen Gründen werden zur Berechnung der maximal erreichbaren Hubhöhe zwei Werte seines Volumens eingeführt: der minimale Vmin bzw. der maximale Vmax. Unter Berücksichtigung der eingeführten Variablen und der Abhängigkeit der Luftdichte von der Höhe haben die Verhältnisse für die Auftriebskraft Fa und die Schwerkraft Ft folgende Form:

, (4)

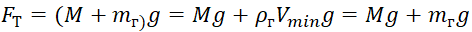
, (5)

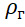
wobei: M die Masse der Hülle und Ausrüstung des stratosphärischen Ballons ist; Ist die Dichte von Helium.

Wenn wir die Beziehungen (4) und (5) gleichsetzen und annehmen, dass das Volumen der Schale V eine Funktion der Höhe des LALV ist, erhalten wir das Verhältnis:

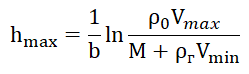
. (6)

Die numerischen Werte der in Beziehung (6) enthaltenen Parameter sind in der Auflistung zur Erstellung eines Graphen angegeben, die nur für den angegebenen Zweck angegeben ist.


Wir bekommen:



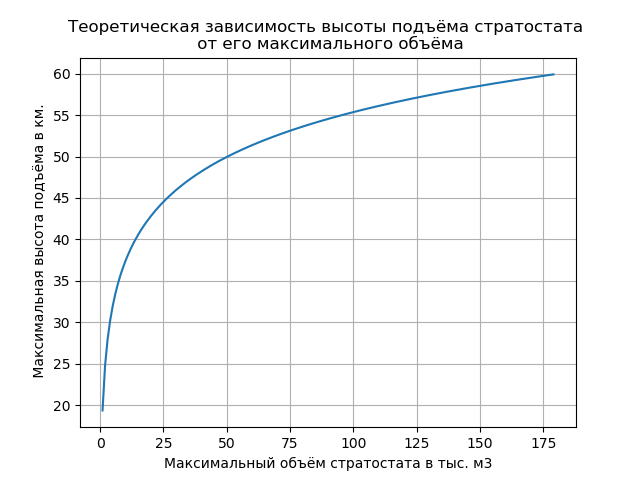
Durch Ändern der in der Programmliste aufgeführten LALV-Parameter können Sie das angegebene Diagramm abrufen und das erforderliche maximale Shell-Volumen während des Entwurfs auswählen. Die Verfeinerung der Ergebnisse erfolgt mit langjähriger Erfahrung bei der Erstellung solcher Geräte.

Schlussfolgerungen:

1. Es werden mathematische Modelle von zwei Flugzeugtypen erhalten, die leichter als Luft sind, die Computerexperimente ermöglichen, um die Parameter solcher Geräte unter idealisierten Bedingungen der Luftumgebung zu bewerten.
   
2. Das vorgeschlagene mehrstufige Schema für die numerische Lösung des Differentialgleichungssystems ermöglicht es, die vertikale Flugbahn von Flugzeugen zu erhalten, die in den Stadien des Anstiegs von Schweben und Sinken leichter als Luft sind.
   

Referenzen

1. Ein paar Worte zu Luftschiffen
   
2. Auf dem Weg ins All. Stratostaten
   
3. Ryzhikov Yu.I. Modernes Fortran. - St. Petersburg: Kronendruck, 2004. - 288 S.