KI, praktischer Kurs. Übersicht über neuronale Netze zur Bildklassifizierung

Dieser Artikel bietet einen zugänglichen theoretischen Überblick über Faltungs-Neuronale Netze (CNN) und erläutert deren Anwendung auf das Bildklassifizierungsproblem.

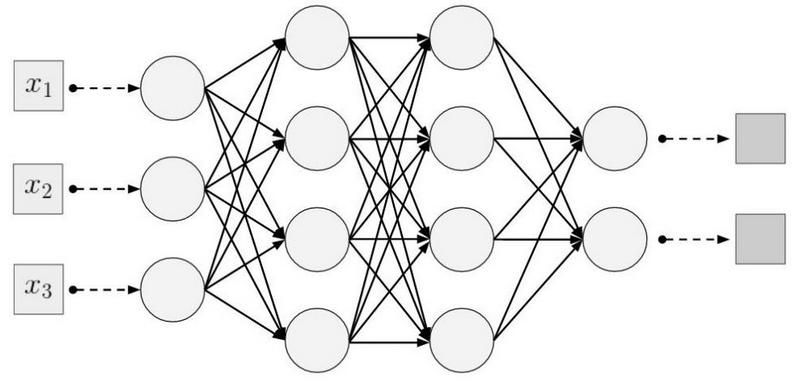
Gemeinsamer Ansatz: Kein tiefes Lernen

Der Begriff "Bildverarbeitung" bezieht sich auf eine breite Klasse von Aufgaben, für die die Eingabedaten Bilder sind, und die Ausgabe kann entweder Bilder oder Sätze von zugehörigen charakteristischen Merkmalen sein. Es gibt viele Optionen: Klassifizierung, Segmentierung, Annotation, Objekterkennung usw. In diesem Artikel untersuchen wir die Klassifizierung von Bildern, nicht nur, weil dies die einfachste Aufgabe ist, sondern auch, weil sie vielen anderen Aufgaben zugrunde liegt.

Der allgemeine Ansatz zur Klassifizierung von Bildern besteht aus den folgenden zwei Schritten:

1. Erzeugung wesentlicher Merkmale des Bildes.
2. Klassifizierung eines Bildes anhand seiner Attribute.

Die übliche Abfolge von Vorgängen verwendet einfache Modelle wie MultiLayer Perceptron (MLP), Support Vector Machine (SVM), die Methode der nächsten Nachbarn und die logistische Regression zusätzlich zu manuell erstellten Funktionen. Attribute werden unter Verwendung verschiedener Transformationen (z. B. Graustufen- und Schwellenwerterkennung) und Deskriptoren erzeugt, z. B. Histogramm orientierter Gradienten ( HOG ) oder skaleninvarianter Merkmalstransformationstransformationen ( SIFT ) und usw.

Die Hauptbeschränkung allgemein anerkannter Methoden besteht in der Teilnahme eines Experten, der einen Satz und eine Abfolge von Schritten zum Generieren von Merkmalen auswählt.

Im Laufe der Zeit wurde festgestellt, dass die meisten Techniken zum Erzeugen von Merkmalen mithilfe von Kerneln (Filtern) verallgemeinert werden können - kleinen Matrizen (normalerweise 5 × 5 groß), die Windungen der Originalbilder sind. Die Faltung kann als ein sequentieller zweistufiger Prozess betrachtet werden:

1. Führen Sie denselben festen Kern über das gesamte Quellbild.
2. Berechnen Sie bei jedem Schritt das Skalarprodukt des Kernels und das Originalbild an der aktuellen Position des Kernels.

Das Ergebnis der Faltung des Bildes und des Kernels wird als Feature-Map bezeichnet.
Eine mathematisch strengere Erklärung findet sich im entsprechenden Kapitel des kürzlich veröffentlichten Buches Deep Learning von I. Goodfellow, I. Benjio und A. Courville.


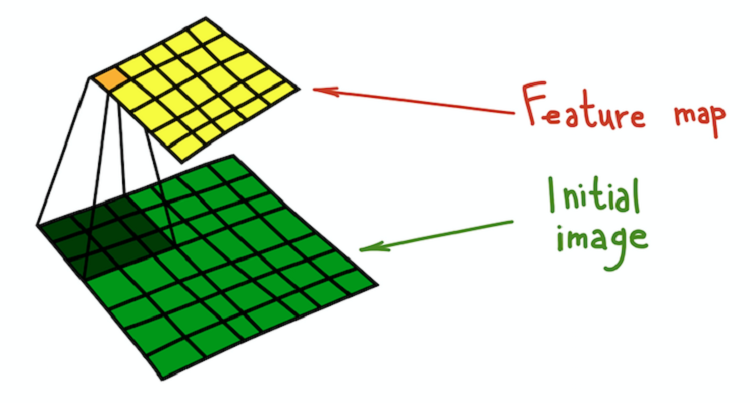Der Prozess der Faltung des Kerns (dunkelgrün) mit dem Originalbild (grün), wodurch eine Merkmalskarte erhalten wird (gelb).

Ein einfaches Beispiel für eine Transformation, die mit Filtern durchgeführt werden kann, ist das Verwischen eines Bildes. Nehmen Sie einen Filter, der aus allen Einheiten besteht. Es berechnet den vom Filter bestimmten Durchschnitt der Nachbarschaft. In diesem Fall ist die Nachbarschaft ein quadratischer Abschnitt, aber sie kann kreuzförmig sein oder was auch immer. Die Mittelung führt zum Verlust von Informationen über die genaue Position von Objekten, wodurch das gesamte Bild unscharf wird. Eine ähnliche intuitive Erklärung kann für jeden manuell erstellten Filter gegeben werden.


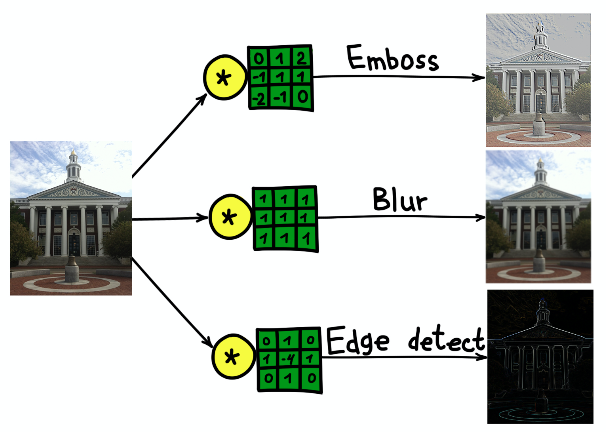Das Ergebnis der Faltung des Bildes des Gebäudes der Harvard University mit drei verschiedenen Kernen.

Faltungsneurale Netze

Der Faltungsansatz zur Bildklassifizierung weist eine Reihe wesentlicher Nachteile auf:

• Ein mehrstufiger Prozess anstelle einer End-to-End-Sequenz.
• Filter sind ein großartiges Verallgemeinerungswerkzeug, aber sie sind feste Matrizen. Wie wählt man Gewichte in Filtern?

Glücklicherweise wurden lernbare Filter erfunden, die das Grundprinzip von CNN darstellen. Das Prinzip ist einfach: Wir werden die Filter trainieren, die auf die Beschreibung von Bildern angewendet werden, um ihre Aufgabe bestmöglich zu erfüllen.

CNN hat keinen Erfinder, aber einer der ersten Fälle ihrer Anwendung ist LeNet-5 * in der Arbeit „ Gradientenbasiertes Lernen für die Dokumentenerkennung“ von I. LeCun und anderen Autoren.

CNN tötet zwei Fliegen mit einer Klappe: Es ist keine vorläufige Definition von Filtern erforderlich, und der Lernprozess wird von Ende zu Ende. Eine typische CNN-Architektur besteht aus folgenden Teilen:

• Faltungsschichten
• Unterabtastungsebenen
• Dichte (vollständig verbundene) Schichten

Lassen Sie uns jeden Teil genauer betrachten.

Faltungsschichten

Die Faltungsschicht ist das Hauptstrukturelement von CNN. Die Faltungsschicht weist eine Reihe von Eigenschaften auf:
Lokale (spärliche) Konnektivität . In dichten Schichten ist jedes Neuron mit jedem Neuron der vorherigen Schicht verbunden (daher wurden sie als dicht bezeichnet). In der Faltungsschicht ist jedes Neuron nur mit einem kleinen Teil der Neuronen der vorherigen Schicht verbunden.


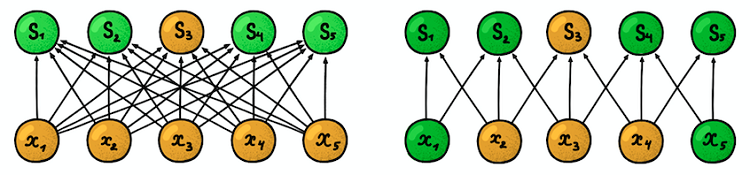Ein Beispiel für ein eindimensionales neuronales Netzwerk. (links) Verbindung von Neuronen in einem typischen dichten Netzwerk, (rechts) Charakterisierung der lokalen Konnektivität, die der Faltungsschicht innewohnt. Bilder von I. Goodfellow und anderen von Deep Learning

Die Größe des Bereichs, mit dem das Neuron verbunden ist, wird als Größe des Filters bezeichnet (die Länge des Filters bei eindimensionalen Daten, z. B. Zeitreihen, oder die Breite / Höhe bei zweidimensionalen Daten, z. B. Bildern). In der Abbildung rechts beträgt die Filtergröße 3. Die Gewichte, mit denen die Verbindung hergestellt wird, werden als Filter bezeichnet (ein Vektor bei eindimensionalen Daten und eine Matrix für zweidimensionale Daten). Der Schritt ist die Entfernung, um die sich der Filter über die Daten bewegt (in der Abbildung rechts ist der Schritt 1). Die Idee der lokalen Konnektivität ist nichts anderes als ein Kernel, der einen Schritt bewegt. Jedes Neuron auf Faltungsebene repräsentiert und implementiert eine bestimmte Position des Kerns, der entlang des Originalbildes gleitet.


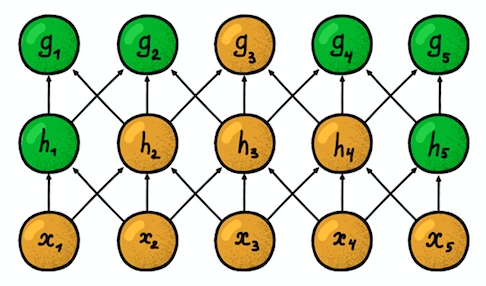Zwei benachbarte eindimensionale Faltungsschichten

Eine weitere wichtige Eigenschaft ist die sogenannte Suszeptibilitätszone . Es spiegelt die Anzahl der Positionen des ursprünglichen Signals wider, die das aktuelle Neuron „sehen“ kann. Beispielsweise ist die in der Figur gezeigte Suszeptibilitätszone der ersten Netzwerkschicht gleich der Größe von Filter 3, da jedes Neuron nur mit drei Neuronen des ursprünglichen Signals verbunden ist. Auf der zweiten Schicht beträgt die Suszeptibilitätszone jedoch bereits 5, da das Neuron der zweiten Schicht drei Neuronen der ersten Schicht aggregiert, von denen jede eine Suszeptibilitätszone 3 aufweist. Mit zunehmender Tiefe wächst die Suszeptibilitätszone linear.

Gemeinsame Parameter . Denken Sie daran, dass bei der klassischen Bildverarbeitung derselbe Kern über das gesamte Bild glitt. Die gleiche Idee gilt hier. Wir legen nur die Größe des Filter der Gewichte für eine Schicht fest und wenden diese Gewichte auf alle Neuronen in der Schicht an. Dies entspricht dem Verschieben desselben Kerns im gesamten Bild. Es kann sich aber die Frage stellen: Wie können wir mit so wenigen Parametern etwas lernen?


Dunkle Pfeile stehen für die gleichen Gewichte. (links) Regulärer MLP, bei dem jeder Gewichtungsfaktor ein separater Parameter ist. (rechts) Ein Beispiel für die Parametertrennung, bei der mehrere Gewichtungsfaktoren denselben Trainingsparameter angeben

Raumstruktur . Die Antwort auf diese Frage ist einfach: Wir werden mehrere Filter in einer Schicht trainieren! Sie sind parallel zueinander angeordnet und bilden so eine neue Dimension.

Wir machen eine kurze Pause und erläutern die Idee am Beispiel eines zweidimensionalen RGB-Bildes von 227 × 227. Beachten Sie, dass es sich hier um ein dreikanaliges Eingabebild handelt, was im Wesentlichen bedeutet, dass wir drei Eingabebilder oder dreidimensionale Eingabedaten haben.


Die räumliche Struktur des Eingabebildes

Wir werden die Abmessungen der Kanäle als Bildtiefe betrachten (beachten Sie, dass dies nicht der Tiefe der neuronalen Netze entspricht, die der Anzahl der Netzwerkschichten entspricht). Die Frage ist, wie der Kernel für diesen Fall bestimmt wird.


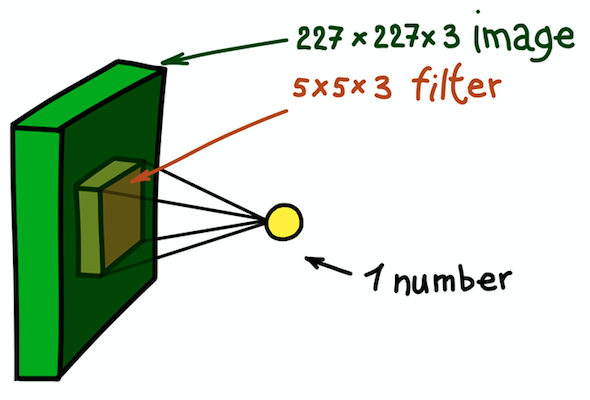
Ein Beispiel für einen zweidimensionalen Kern, bei dem es sich im Wesentlichen um eine dreidimensionale Matrix mit einer zusätzlichen Tiefenmessung handelt. Dieser Filter ergibt eine Faltung mit dem Bild; Das heißt, es gleitet über das Bild im Raum und berechnet skalare Produkte

Die Antwort ist einfach, aber immer noch nicht offensichtlich: Wir werden den Kernel auch dreidimensional machen. Die ersten beiden Dimensionen bleiben gleich (Kernbreite und -höhe), und die dritte Dimension entspricht immer der Tiefe der Eingabedaten.


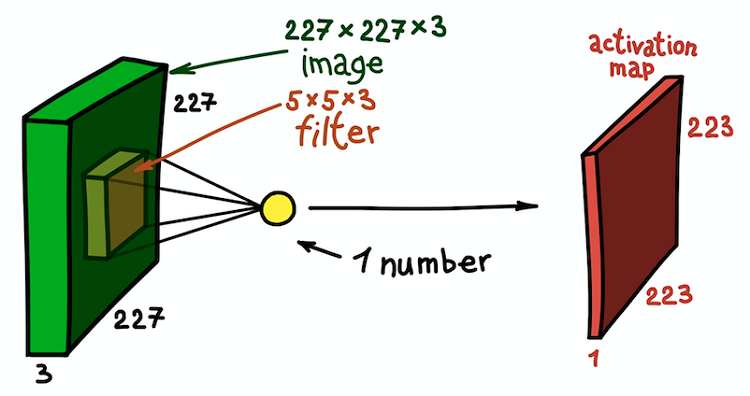
Ein Beispiel für einen räumlichen Faltungsschritt. Das Ergebnis des Skalarprodukts des Filters und eines kleinen Teils des Bildes 5 × 5 × 3 (d. H. 5 × 5 × 5 + 1 = 76, die Dimension des Skalarprodukts + Verschiebung) ist eine Zahl

In diesem Fall wird der gesamte 5 × 5 × 3-Abschnitt des Originalbilds in eine Zahl umgewandelt, und das dreidimensionale Bild selbst wird in eine Merkmalskarte ( Aktivierungskarte ) umgewandelt. Eine Feature-Map ist eine Reihe von Neuronen, von denen jede ihre eigene Funktion berechnet, wobei zwei oben diskutierte Grundprinzipien berücksichtigt werden: lokale Konnektivität (jedes Neuron ist nur einem kleinen Teil der Eingabedaten zugeordnet) und Trennung von Parametern (alle Neuronen verwenden denselben Filter). Im Idealfall ist diese Feature-Map dieselbe wie die, die bereits im Beispiel eines allgemein akzeptierten Netzwerks angetroffen wurde. Sie speichert die Ergebnisse der Faltung des Eingabebilds und des Filters.


Merkmalskarte als Ergebnis der Faltung des Kerns mit allen räumlichen Positionen

Beachten Sie, dass die Tiefe der Feature-Map 1 beträgt, da wir nur einen Filter verwendet haben. Aber nichts hindert uns daran, mehr Filter zu verwenden. Beispiel: 6. Alle interagieren mit denselben Eingabedaten und arbeiten unabhängig voneinander. Gehen wir noch einen Schritt weiter und kombinieren diese Funktionskarten. Ihre räumlichen Abmessungen sind gleich, da die Abmessungen der Filter gleich sind. Somit können die zusammen gesammelten Merkmalskarten als eine neue dreidimensionale Matrix betrachtet werden, deren Tiefenabmessung durch Merkmalskarten aus verschiedenen Kernen dargestellt wird. In diesem Sinne sind die RGB-Kanäle des Eingabebildes nichts anderes als die drei ursprünglichen Feature-Maps.


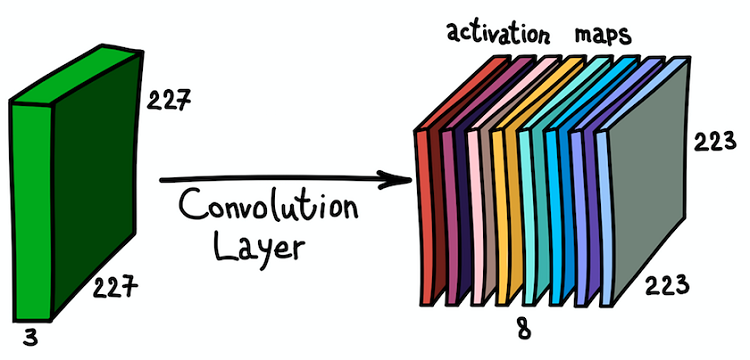Die parallele Anwendung mehrerer Filter auf das Eingabebild und den daraus resultierenden Satz von Aktivierungskarten

Ein solches Verständnis der Feature-Maps und ihrer Kombination ist sehr wichtig, da wir, nachdem wir dies erkannt haben, die Netzwerkarchitektur erweitern und Faltungsschichten übereinander installieren können, wodurch die Suszeptibilitätszone erhöht und unser Klassifikator angereichert wird.


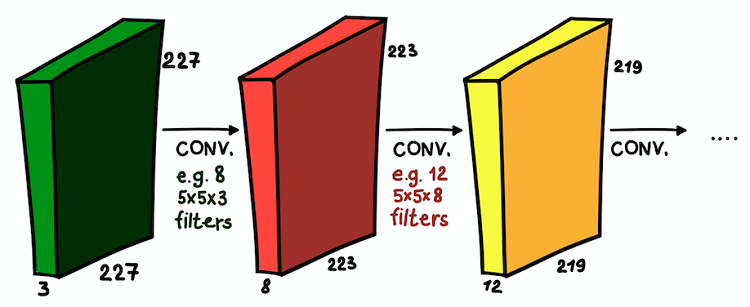Übereinander installierte Faltungsschichten. In jeder Schicht können die Größe der Filter und ihre Anzahl variieren

Jetzt verstehen wir, was ein Faltungsnetzwerk ist. Das Hauptziel dieser Schichten ist das gleiche wie beim allgemein akzeptierten Ansatz - signifikante Zeichen des Bildes zu erkennen. Und wenn diese Zeichen in der ersten Schicht sehr einfach sein können (das Vorhandensein vertikaler / horizontaler Linien), erhöht die Tiefe des Netzwerks den Grad ihrer Abstraktion (das Vorhandensein eines Hundes / einer Katze / einer Person).

Unterabtastungsebenen

Faltungsschichten sind der Hauptbaustein von CNN. Aber es gibt noch einen anderen wichtigen und häufig verwendeten Teil - dies sind Unterprobenschichten. Bei der herkömmlichen Bildverarbeitung gibt es kein direktes Analogon, aber eine Unterprobe kann als eine andere Art von Kernel betrachtet werden. Was ist das


Beispiele für Unterabtastung. (links) Wie ein Teilmuster die räumlichen (aber nicht die Kanal!) Größen von Datenarrays ändert. (rechts) Ein grundlegendes Schema für die Funktionsweise eines Teilmusters

Eine Unterabtastung filtert einen Teil der Nachbarschaft jedes Pixels der Eingabedaten mit einer bestimmten Aggregationsfunktion, beispielsweise Maximum, Durchschnitt usw. Die Unterabtastung entspricht im Wesentlichen der Faltung, aber die Pixelkombinationsfunktion ist nicht auf das Skalarprodukt beschränkt. Ein weiterer wichtiger Unterschied besteht darin, dass die Unterabtastung nur in der räumlichen Dimension funktioniert. Ein charakteristisches Merkmal der Unterabtastschicht ist, dass der Abstand normalerweise gleich der Größe des Filters ist (der typische Wert ist 2).

Eine Teilstichprobe hat drei Hauptziele:

• Verringerung der räumlichen Dimension oder Unterabtastung. Dies geschieht, um die Anzahl der Parameter zu verringern.
• Das Wachstum der Suszeptibilitätszone. Aufgrund der Teilprobenneuronen in den nachfolgenden Schichten werden mehr Schritte des Eingangssignals akkumuliert
• Translationale Invarianz zu kleinen Heterogenitäten in der Position der Muster im Eingangssignal. Durch Berechnung der Aggregationsstatistik kleiner Nachbarschaften des Eingangssignals kann eine Teilstichprobe kleine räumliche Verschiebungen darin ignorieren.

Dicke Schichten

Faltungsebenen und Unterabtastebenen dienen demselben Zweck - sie erzeugen Bildattribute. Der letzte Schritt besteht darin, das Eingabebild anhand der erkannten Merkmale zu klassifizieren. Bei CNN tun dies dichte Schichten über dem Netzwerk. Dieser Teil des Netzwerks wird als Klassifizierung bezeichnet . Es kann mehrere Ebenen mit vollständiger Konnektivität übereinander enthalten, endet jedoch normalerweise mit einer Softmax- Klassenebene, die durch eine logistische Aktivierungsfunktion mit mehreren Variablen aktiviert wird, bei der die Anzahl der Blöcke der Anzahl der Klassen entspricht. Am Ausgang dieser Schicht befindet sich die Wahrscheinlichkeitsverteilung nach Klasse für das Eingabeobjekt. Jetzt kann das Bild klassifiziert werden, indem die wahrscheinlichste Klasse ausgewählt wird.