"Aber wir machen Raketen!"

In einem früheren Artikel habe ich geprüft, ob es möglich ist, einen Fuzzy-Controller mithilfe von „Standardmethoden“ zur Optimierung automatisch anzupassen. Es stellte sich als möglich heraus und das Ergebnis der automatischen Abstimmung ist ziemlich zufriedenstellend. Zumindest für die Rakete, deren Modell verwendet wurde.

Bei instationären Steuerobjekten, bei denen die Objektparameter über große Bereiche variieren, bietet eine Fuzzy-Steuerung möglicherweise nicht in allen Betriebsbereichen eine ausreichende Steuerqualität. In diesem Fall muss ein Fuzzy-Controller mit „Mehrkanal-Tuning“ verwendet werden.

Lassen Sie uns prüfen, ob es möglich ist, einen solchen Regler mit Standardoptimierungsmethoden zu konfigurieren.
Betrachten Sie die Synthese eines Fuzzy-Controllers mit Mehrkanal-Tuning, um eine ballistische Rakete im Nickwinkel zu stabilisieren. Wie in den Kommentaren angegeben, wird die Rakete FAU-2 sein. Wir verwenden ein Beispiel aus demselben Buch von V. Gostev. "Fuzzy-Regler in automatischen Steuerungssystemen."

Alle in diesem Text verwendeten Begriffe stammen aus diesem Buch und entsprechen möglicherweise nicht der strengen Terminologie der Theorie der automatischen Steuerung.

Erklärung des Problems

Eine ballistische Rakete, die eine große Anzahl lokaler Steuerungssysteme verwendet, ist ein im Wesentlichen instationäres Steuerobjekt. Die Übertragungsfunktionen, die die Rakete als Steuerobjekt beschreiben, unterscheiden sich von den Übertragungsfunktionen von geflügelten Flugzeugen darin, dass sie instabile Verbindungen aufweisen, so dass die Bewegung einer unkontrollierten Rakete entlang eines programmierten Pfades instabil wäre.

Nachfolgend betrachten wir das Stabilisierungssystem eines ballistischen Flugkörpers im Nickwinkel (Längsbewegungskanal). Das System besteht aus folgenden funktional notwendigen Elementen:
ein Vergleichselement (ein freier Kreisel mit einem potentiometrischen Sensor, der durch Kp-Koeffizienten gekennzeichnet ist);
Leistungsverstärker Ku und hydraulisches Lenkgetriebe.

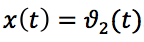
Nehmen Sie den Nickwinkel als Austrittskoordinate der Rakete , für die Eingangskoordinate - Lenkwinkel definieren wir die Übertragungsfunktion in der Form:


(Das analoge Lenkgetriebe und die Rakete sind im Steuerobjekt enthalten.) Die Parameter der Übertragungsfunktion sind zeitabhängige Polynome. Mathematisch können sie durch Polynome bestimmt werden:











Die Aufgabe setzt voraus, dass die Flugstartzeit 6 Sekunden beträgt. Polynomwerte werden mit einer Verschiebung von 6 Sekunden akzeptiert.
Das mathematische Modell der instationären Schwingungsverbindung wird durch die Differentialgleichung beschrieben:



Das mathematische Modell einer instationären Forcierungsverbindung wird durch die Differentialgleichung beschrieben:



Der Fehlanpassungsfehler am Eingang des Fuzzy-Reglers ist die Differenz zwischen dem eingestellten und dem erforderlichen Nickwinkel.

Das Strukturdiagramm des Modells ist in Abbildung 1 dargestellt. Um das Prinzip der Modellbildung zu verstehen, geben die Kommunikationsleitungen die Variablen X1, X und ihre Ableitungen ( X1 '', X1 '', X ' ) gemäß den Gleichungen der Verbindungen an. Das grüne Rechteck zeigt den Teil der Modellschaltung an, der der oszillierenden Verbindung entspricht, und das gelbe ist die forcierende Verbindung.

Die Parameter a (t), b (t), c (t), r (t) werden in Form von Verstärkungsfaktoren in Blöcken vom Typ "Verstärker" eingestellt. Parameter wird in der Verstärkung der integrierenden Verbindung eingestellt.


Abbildung 1. Strukturdiagramm des Modells.

Softwarepfad bei gegebenem Nickwinkel u (t) = 1 + 0,5 sin (πt / 30).
Diagramme der Änderungen der Raketenparameter während des Fluges sind in Abbildung 2 dargestellt.
Der Wert von t = 6 wird als Start des Fluges genommen, in der Polynomfunktion wird der Wert (Zeit + 6) verwendet, um die Parameter zu berechnen, wobei Zeit die aktuelle Simulationszeit ist.


Abbildung 2. Diagramme der Änderungen der Raketenparameter.

Fuzzy-Logik-Controller

Als Controller, der auf Fuzzy-Logik basiert, verwenden wir den in Abbildung 3 gezeigten Controller. Eine Fehlanpassung zwischen dem angegebenen Nickwinkel und dem realen Raketenwinkel wird an den Eingang angelegt.

Die Blockverzögerung pro Quantisierungsschritt liefert eine Diskretisierung der Umwandlung eines kontinuierlichen Signals in ein diskretes mit einem Abtastschritt von 0,01 Sekunden.

Unter Verwendung von zwei weiteren Verzögerungen werden die Abweichungen der ersten und zweiten Ableitung durch die Differenzmethoden im Diskretisierungsschritt berechnet.

Phaseneinheiten berechnen die Werte der Terme für Abweichung, Änderungsrate und Beschleunigung. (Mehr dazu im vorherigen Text ). Am Ausgang jedes Phasenblocks erhalten wir einen Termvektor für sprachliche Variablen. (siehe Tabelle 1)

Sprachvariable	Bedingungen
Abweichung	Mehr Norm Weniger
Änderungsrate	Wächst Ändert sich nicht Fällt
Schnellere Änderung	Steigt Konstante Verringert sich

Die Demultiplexerblöcke analysieren die Vektoren in separate Terme, die gemäß den Fuzzy-Inferenzregeln an die logischen Verarbeitungsblöcke übertragen werden.
Das Ergebnis der Fuzzy-Inferenz hat auch drei sprachliche Variablen: "reduzieren", "nicht ändern", "erhöhen". Die folgenden Inferenzregeln werden in Form eines Diagramms geschrieben.

• Wenn mehr und Wachstum und Wachstumsrate zunehmen => abnehmen .
• Wenn sich die Norm nicht ändert und konstant ist => ändern wir uns nicht .
• Wenn weniger und fällt und die Fallrate steigt => erhöhen .

Abbildung 3. Schema eines Reglers basierend auf Fuzzy-Logik.

Bei der Entnazifizierung werden Dreiecksfunktionen mit einer gemeinsamen Basis als Zugehörigkeitsfunktion verwendet (siehe Abb. 4).

Abbildung 4. Dreieckige Phasenfunktionen mit einer gemeinsamen Basis.

Es wird angenommen, dass die Funktionen in Bezug auf 0 symmetrisch sind. In diesem Fall ist ein Wert von Max ausreichend, um drei Dreiecksfunktionen zu beschreiben. Für die in der Abbildung gezeigten ist Max = 30.

Für die Ausgabe werden dieselben Zugehörigkeitsfunktionen verwendet.

Für eine vollständige Definition des Reglers müssen die Maximalwerte für die Blöcke der Phasenvariablenisierung von Variablen festgelegt werden:

- deltaMax - maximale Abweichung;
- divMax - die maximale Ableitung der Abweichung;
- div2Max - maximale zweite Ableitung der Abweichung;
- uMax - maximale Steueraktion.

Vollständige Prozessoptimierung

Die maximale Steueraktion entspricht uMax - 70.
Es bleibt uns also überlassen, 3 Parameter für die Phasenverschiebungsfunktion zu wählen.
In diesem Problem wird die Fehlanpassung durch einen Schritt zum Nullzeitpunkt der Modellzeit u (t) = 1 + 0,5 sin (πt / 30) gespeist.

Die programmierte Trajektorie, der gegebene Nickwinkel u (t) = 1 + 0,5sin (πt / 30), bewirkt einen schrittweisen Effekt in der ersten Sekunde des Übergangsprozesses, wie sich bei Experimenten mit der vorherigen Aufgabe herausstellte, können Regler, die auf einen reibungslosen Steuerungsprozess mit schrittweiser Aktion abgestimmt sind, können nicht die erforderliche Qualität des Übergangsprozesses liefern.

Daher bilden wir zur Optimierung drei Kriterien:

1. Übergangszeit - Wir müssen so schnell wie möglich zu einem bestimmten Programmpfad gelangen.
2. Standardabweichung.
3. Anzahl der Schaltvorgänge - In Experimenten mit der vorherigen Aufgabe erhielten wir die Option, wenn am Ausgang des Steuerungssystems hochfrequente Schwingungen der Steueraktion auftraten.

Das allgemeine Schema des Optimierungsblocks ist in Abbildung 5 dargestellt.

Abbildung 5. Schema des Optimierungsblocks.

Eingabeparameter des Optimierungsblocks:

- Abweichung vom angegebenen Nickwinkel.
- regulatorische Auswirkungen.

Zur Berechnung der Übergangszeit wird ein Schalter verwendet, bei dem die aktuelle Modellzeit auf einen der Eingänge angewendet wird. Nach dem Block gibt es eine Verzögerung für die Quantisierungsperiode, der Wert von der Verzögerung wird an den zweiten Eingang übertragen.

Als Schalter wird ein Abweichungsmodul verwendet. Wenn das Abweichungsmodul größer als der eingestellte Schaltwert (0,02) ist, wird die aktuelle Zeit am Block ausgegeben. Wenn das Modul kleiner als der eingestellte Wert ist, wird die Zeit, die gespeichert wurde, als die Abweichung größer war, an den Ausgang übertragen. Wenn die Abweichung die Grenze erneut überschreitet, erhalten wir erneut die Zeit. Somit haben wir am Ausgang immer das letzte Mal, wenn die Abweichung den eingestellten Wert überschreitet.
Als Schalteinheit wird das Vorzeichen der Steueraktion von + auf - geändert. Um die Anzahl der Schaltvorgänge zu berechnen, verwenden wir den Block „Impuls entlang der Vorderseite“, der, wenn der Eingang von 0 auf 1 geändert wird, im Integrationsschritt einen Impuls von Dauer ergibt. Die Impulse werden vom Integrator berechnet. Am Ausgang des Blocks - die Anzahl der Schaltvorgänge.

- Der Optimierungsblock wählt die Werte der zu optimierenden Parameter so aus, dass alle drei Parameter minimiert werden:
- deltaMax - maximale Abweichung;
- divMax - die maximale Ableitung der Abweichung;
- div2Max - die maximale zweite Ableitung der Abweichung.

Das Ergebnis ist eine Optimierung des gesamten Übergangsprozesses.

Nachdem wir den Optimierungsprozess gestartet haben, haben wir die folgenden optimalen Parameter für den Fuzzy-Controller erhalten:

- deltaMax = 0,185 - maximale Abweichung;
- divMax = 0,278 - die maximale Ableitung der Abweichung;
- div2Max = 1.291 - die maximale zweite Ableitung der Abweichung.

Die Ergebnisse des optimierten Prozesses sind in Abbildung 6 dargestellt.

Abbildung 6a. Der Übergangsprozess.

Abbildung 6b. Steuerungsoptionen.

Es ist ersichtlich, dass die Optimierung insgesamt ein Erfolg war, aber Abweichungen vom gegebenen Nickwinkel bestehen fast während des gesamten Prozesses. Das vergrößerte Abweichungsdiagramm zeigt, dass die Abweichungen nach der Optimierung und dem Abschluss des Übergangsprozesses im Bereich von 0,015 bis 0,02 liegen. (siehe Abb. 7)

Abbildung 7. Abweichung im Steuerungsprozess.

Optimierung nach Flugabschnitten.

Versuchen wir, den Prozess zu verbessern, indem wir die Parameter des Fuzzy-Controllers für verschiedene Abschnitte des Raketenfluges auswählen.

Der erste Abschnitt ist die Zeit vom Start bis zum Verlassen eines bestimmten Pfades. Basierend auf dem Abweichungsdiagramm endet der mit dem anfänglichen schrittweisen Effekt verbundene Übergangsprozess irgendwo bei 20 Sekunden. (siehe Abb. 7). In diesem Abschnitt erfolgt die zeitliche Optimierung des Übergangsprozesses.

Stellen Sie die Endzeit der Berechnung auf 20 Sekunden ein. Und wir werden die Optimierung durchführen und die Standardabweichung von den Kriterien entfernen. Wir werden den Zeitpunkt des Übergangsprozesses und die Anzahl der Umschaltungen optimieren. Das Optimierungsblockdiagramm ist in Abbildung 8 dargestellt.


Abbildung 8. Optimierungsschema in der ersten Flugphase.

Die automatische Optimierung für die erste Flugphase bis zu 20 Sekunden ergab die folgenden Parameter für die Fuzzy-Regelung:

- deltaMax = 0,056 - maximale Abweichung;
- divMax = 0,0968 - die maximale Ableitung der Abweichung;
- div2Max = 0,987 - die maximale zweite Ableitung der Abweichung.

Der Übergangsprozess nach der Optimierung ist in Abbildung 9 dargestellt.

Abweichungen in größerem Maßstab sind in Abbildung 10 dargestellt.

Abbildung 9a. Der Übergangsprozess.

Abbildung 9b. Steuerungsoptionen.

Abbildung 10. Größere Skalenabweichung des ersten Flugabschnitts.

Die Grafiken zeigen, dass das Überschwingen abnahm und die Abweichung nach dem Ende des Übergangsprozesses weniger als 0,005 betrug.

Zur Optimierung im nächsten Flugabschnitt führen wir die Simulation mit dem im ersten Abschnitt erhaltenen gespeicherten Zustand durch.

Die Simulation erfolgt zwischen 20 und 40 Sekunden im Flug mit ballistischen Raketen. Die Optimierung erfolgt während des gesamten Prozesses.

Da wir den Übergangsprozess zu Beginn des zweiten Abschnitts abgeschlossen haben, führen wir die Optimierung nur anhand der Abweichung und der Anzahl der Schalter durch. Das Optimierungsblockdiagramm ist in Abbildung 11 dargestellt.


Abbildung 11. Optimierungsschema für den zweiten Flugabschnitt.

Die automatische Optimierung für die zweite Phase des Fluges von 20 bis 40 Sekunden ergab die folgenden Parameter für die Fuzzy-Regelung:

- deltaMax = 0,056 - maximale Abweichung;
- divMax = 0,0974 - die maximale Ableitung der Abweichung;
- div2Max = 0,980 - die maximale zweite Ableitung der Abweichung.

Mit den gegebenen Parametern nimmt die Abweichung des Nickwinkels von dem gegebenen über den gesamten zweiten Zeitabschnitt des Fluges ab. Wenn wir jedoch die durch Optimierung im zweiten Teil des Flugs erhaltenen Parameter verwenden, um bis zu 66 Sekunden zu steuern, ist ersichtlich, dass die Genauigkeit abnimmt und die Abweichung nach 40 Sekunden zuzunehmen beginnt (siehe Abb. 12).


Abbildung 12. Prozess zur Steuerung ballistischer Raketen mit Einstellungen, die für einen Flug von 20 bis 40 Sekunden optimiert sind.

Wiederholen Sie die Optimierung für die dritte Flugstrecke. Speichern Sie die Ergebnisse für 40 Sekunden.

Wir verwenden sie, um in einem Abschnitt von 40 bis 66 Sekunden zu starten und zu optimieren.

Die automatische Optimierung für den letzten Flugabschnitt von 40 bis 66 Sekunden ergab die folgenden Parameter für die Fuzzy-Regelung:

- deltaMax = 0,0146 - maximale Abweichung;
- divMax = 0,0157 - die maximale Ableitung der Abweichung;
- div2Max = 0,555 - die maximale zweite Ableitung der Abweichung.

Das Diagramm des Steuerungsprozesses im letzten Abschnitt des Flugs mit ballistischen Raketen nach der Optimierung ist in Abbildung 13 dargestellt.

Abbildung 13. Prozess zur Kontrolle ballistischer Raketen im letzten Flugabschnitt.

Abbildung 13 zeigt, dass mit den neuen Einstellungen die Abweichung im Flugzeitintervall von 40-66 Sekunden im Gegensatz zu den für das zweite Flugsegment optimierten Einstellungen nicht zunimmt (siehe Abbildung 12).

Somit haben wir die Einstellungen des Fuzzy-Controllers für drei Flugabschnitte erhalten. Lassen Sie uns einen Modusschalter erstellen, der die Controller-Einstellungen während des Fluges ändert. Die Modusschalterschaltung ist in Abbildung 14 dargestellt.


Abbildung 14. Modusschalter des Fuzzy Ballistic Missile Controllers.

Die Schaltmodi finden zeitlich statt. Im oberen Teil vergleicht eine einfache Logikschaltung die aktuelle Modellzeit mit den Schaltpunkten. Infolgedessen wird im Multiplexer ein Steuervektor mit drei Werten gebildet. In diesem Vektor befindet sich der Wert 1 an der Position des aktuellen Zeitintervalls.

Die zuvor durch Optimierungsverfahren berechneten Parameter des Fuzzy-Reglers werden in Vektoren mit drei Werten gepackt.

Mit Hilfe eines Abtastblocks mit drei Werten wird einer ausgewählt, der 1 im Steuervektor entspricht. Wenn sich also die Zeit ändert, ändern sich die an den Fuzzy-Controller übertragenen Parameter entsprechend dem aktuellen Flugabschnitt.

Zur Verdeutlichung werden die über die Kommunikationsleitung übertragenen Werte im Diagramm angezeigt. Die Abbildung entspricht dem letzten Abschnitt eines Fluges mit ballistischen Raketen. Die Zeit beträgt mehr als 40 Sekunden. Der Steuervektor (0,0,1) in der Steuerung ist der letzte Parameter aus dem Satz.

Das Simulationsergebnis der Steuerung des Nickwinkels der Rakete durch Umschalten der Parameter des Reglers ist in Abbildung 15 dargestellt.

Abbildung 15a. Der Übergangsprozess.

Abbildung 15b. Steuerungsoptionen.

Schlussfolgerungen:
Eine auf Fuzzy-Logik basierende Steuerung kann durch das Optimierungsverfahren so konfiguriert werden, dass sie im Parameterumschaltmodus arbeitet.

Die Abweichung beim Arbeiten mit variablen Parametern im angegebenen Beispiel hat sich im Vergleich zum Betrieb des Reglers mit konstanten Parametern um das 3-5-fache verringert.

Das Archiv mit Projekten für unabhängige Studien kann hier heruntergeladen werden ...