Das allgemeine Wesen von Einfügungssortierungen ist wie folgt:
- Iteriert über die Elemente im unsortierten Teil des Arrays.
- Jedes Element wird an der Stelle, an der es sein sollte, in den sortierten Teil des Arrays eingefügt.
Dies ist im Prinzip alles, was Sie über das Sortieren nach Beilagen wissen müssen. Das heißt, Einfügungssortierungen teilen das Array immer in zwei Teile - sortiert und unsortiert. Jedes Element wird aus dem unsortierten Teil abgerufen. Da der andere Teil des Arrays sortiert ist, können Sie schnell Ihren Platz in diesem Array für dieses extrahierte Element finden. Das Element wird bei Bedarf eingefügt, wodurch der sortierte Teil des Arrays zunimmt und der unsortierte Teil abnimmt. Das ist alles. Alle Arten von Einsätzen arbeiten nach diesem Prinzip.
Der schwächste Punkt bei diesem Ansatz ist das Einfügen eines Elements in den sortierten Teil des Arrays. Tatsächlich ist es nicht einfach und welche Tricks Sie nicht ausführen müssen, um diesen Schritt abzuschließen.
Einfache Einfügesortierung

Wir gehen das Array von links nach rechts durch und verarbeiten jedes Element nacheinander. Links vom nächsten Element vergrößern wir den sortierten Teil des Arrays, rechts im Verlauf des Prozesses verdunstet der unsortierte Teil langsam. Im sortierten Teil des Arrays wird die Einfügemarke für das nächste Element gesucht. Das Element selbst wird an den Puffer gesendet, wodurch eine leere Zelle im Array angezeigt wird. Auf diese Weise können Sie die Elemente verschieben und die Einfügemarke freigeben.
def insertion(data): for i in range(len(data)): j = i - 1 key = data[i] while data[j] > key and j >= 0: data[j + 1] = data[j] j -= 1 data[j + 1] = key return data
Am Beispiel einfacher Einfügungen sieht der Hauptvorteil der meisten (aber nicht aller!) Sortieren nach Einfügungen demonstrativ aus, nämlich die sehr schnelle Verarbeitung fast geordneter Arrays:

In diesem Szenario wird wahrscheinlich sogar die primitivste Implementierung von Sortiereinsätzen den superoptimierten Algorithmus für eine schnelle Sortierung überholen, auch bei großen Arrays.
Dies wird durch die Hauptidee dieser Klasse erleichtert - die Übertragung von Elementen vom unsortierten Teil des Arrays zum sortierten. Bei unmittelbarer Nähe von Daten ähnlicher Größe befindet sich die Einfügemarke normalerweise nahe der Kante des sortierten Teils, sodass Sie mit dem geringsten Overhead einfügen können.
Es gibt nichts Besseres für die Handhabung fast geordneter Arrays als die Sortierung nach Einfügungen. Wenn Sie irgendwo auf Informationen stoßen, dass die beste zeitliche Komplexität beim Sortieren nach Einfügungen
O ( n ) ist , beziehen Sie sich höchstwahrscheinlich auf Situationen mit fast geordneten Arrays.
Sortieren Sie nach einfachen binären Sucheinfügungen

Da der einzufügende Ort im sortierten Teil des Arrays gesucht wird, bietet sich die Idee an, eine binäre Suche zu verwenden. Eine andere Sache ist, dass die Suche nach der Einfügungsstelle für die zeitliche Komplexität des Algorithmus nicht kritisch ist (der Hauptressourcenfresser ist die Phase des Einfügens des Elements in die gefundene Position selbst), weshalb diese Optimierung wenig bewirkt.
Und im Fall eines fast sortierten Arrays kann eine binäre Suche noch langsamer arbeiten, da sie in der Mitte des sortierten Abschnitts beginnt, der höchstwahrscheinlich zu weit vom Einfügepunkt entfernt ist (und weniger Schritte benötigt, um eine normale Suche von der Elementposition zum Einfügepunkt durchzuführen, wenn die Daten vorliegen im gesamten Array bestellt).
def insertion_binary(data): for i in range(len(data)): key = data[i] lo, hi = 0, i - 1 while lo < hi: mid = lo + (hi - lo) // 2 if key < data[mid]: hi = mid else: lo = mid + 1 for j in range(i, lo + 1, -1): data[j] = data[j - 1] data[lo] = key return data
Zur Verteidigung der binären Suche stelle ich fest, dass er das letzte Wort in der Wirksamkeit anderer Sortierungen durch Einfügungen sagen kann. Insbesondere dank ihm gehen Algorithmen wie Bibliothekarensortierung und Solitärsortierung auf die durchschnittliche Zeitkomplexität
O ( n log n ) . Aber später darüber.
Paarsortierung nach einfachen Einsätzen
Modifikation einfacher Beilagen, entwickelt in den geheimen Labors der Oracle Corporation. Diese Sortierung ist Teil des JDK und Teil des Dual-Pivot Quicksort. Es wird verwendet, um kleine Arrays (bis zu 47 Elemente) und kleine Bereiche großer Arrays zu sortieren.

Nicht ein, sondern zwei benachbarte Elemente werden gleichzeitig an den Puffer gesendet. Zuerst wird das größere Element des Paares eingefügt, und unmittelbar danach wird die einfache Einfügemethode auf das kleinere Element des Paares angewendet.
Was gibt es? Einsparungen bei der Bearbeitung eines kleineren Artikels aus einem Paar. Für ihn werden die Suche nach der Einfügemarke und die Einfügung selbst nur für den sortierten Teil des Arrays ausgeführt, der nicht den sortierten Bereich enthält, der zum Verarbeiten eines größeren Elements aus dem Paar verwendet wird. Dies wird möglich, weil die größeren und kleineren Elemente unmittelbar nacheinander in einem Durchgang der äußeren Schleife verarbeitet werden.
Dies hat keinen Einfluss auf die durchschnittliche Zeitkomplexität (sie bleibt immer noch gleich
O ( n 2 )) . Gepaarte Inserts arbeiten jedoch etwas schneller als übliche.
Ich illustriere die Algorithmen in Python, aber hier gebe ich die Originalquelle (aus Gründen der Lesbarkeit geändert) in Java an:
for (int k = left; ++left <= right; k = ++left) {
Shell Sort

Dieser Algorithmus hat einen sehr witzigen Ansatz bei der Bestimmung, welcher Teil des Arrays als sortiert betrachtet wird. In einfachen Einfügungen ist alles einfach: Vom aktuellen Element ist alles links bereits sortiert, alles rechts ist noch nicht sortiert. Im Gegensatz zu einfachen Einfügungen versucht die Shell-Sortierung nicht sofort, einen streng sortierten Teil des Arrays links von einem Element zu bilden. Es erstellt einen
fast sortierten Teil des Arrays links vom Element und erledigt dies schnell genug.
Die Shell-Sortierung wirft das aktuelle Element in den Puffer und vergleicht es mit der linken Seite des Arrays. Wenn links größere Elemente gefunden werden, werden diese nach rechts verschoben, sodass Platz zum Einfügen vorhanden ist. Gleichzeitig nimmt es aber nicht den gesamten linken Teil, sondern nur eine bestimmte Gruppe von Elementen, wobei die Elemente um einen bestimmten Abstand voneinander beabstandet sind. Mit einem solchen System können Sie Elemente schnell in ungefähr den Bereich des Arrays einfügen, in dem sie sich befinden sollten.
Mit jeder Iteration der Hauptschleife nimmt dieser Abstand allmählich ab, und wenn er gleich eins wird, verwandelt sich die Shell-Sortierung in diesem Moment in eine klassische Sortierung mit einfachen Einfügungen, die für die Verarbeitung eines fast sortierten Arrays verwendet wurden. Eine fast sortierte Array-Sortierung fügt schnell in vollständig sortierte Konvertierungen ein.
def shell(data): inc = len(data) // 2 while inc: for i, el in enumerate(data): while i >= inc and data[i - inc] > el: data[i] = data[i - inc] i -= inc data[i] = el inc = 1 if inc == 2 else int(inc * 5.0 / 11) return data
Die Kammsortierung nach einem ähnlichen Prinzip verbessert die Blasensortierung, sodass die zeitliche Komplexität des Algorithmus mit
O ( n 2 ) bis zu
O ( n log n ) springt. Leider schafft es Shell nicht, dieses Kunststück zu wiederholen - die beste Zeitkomplexität erreicht
O ( n log 2 n ) .
Es wurden mehrere Habrastati über das Sortieren von Shell geschrieben, damit wir nicht mit Informationen überladen werden und weitermachen.
Baumsortierung
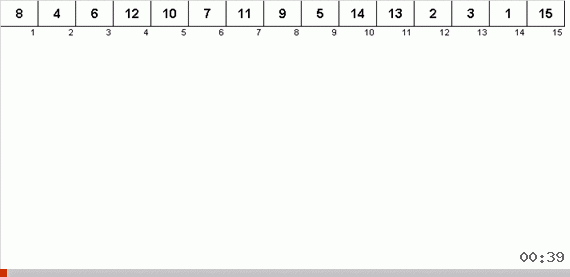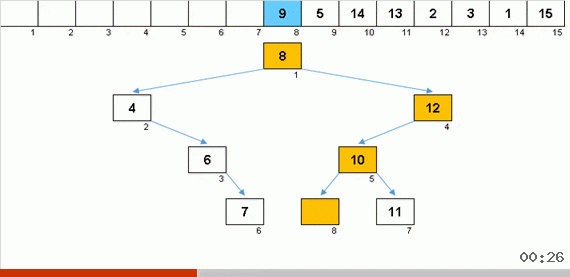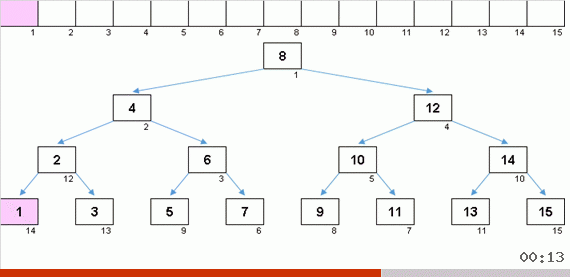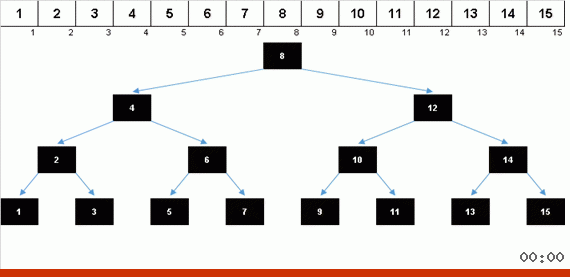
Das Sortieren mit einem Baum aufgrund zusätzlichen Speichers löst schnell das Problem, dem sortierten Teil des Arrays ein weiteres Element hinzuzufügen. Darüber hinaus fungiert der Binärbaum als sortierter Teil des Arrays. Ein Baum wird buchstäblich im laufenden Betrieb gebildet, wenn Elemente durchlaufen werden.
Das Element wird zuerst mit der Wurzel und dann mit mehr verschachtelten Knoten nach dem Prinzip verglichen: Wenn das Element kleiner als der Knoten ist, gehen wir den linken Zweig hinunter, wenn nicht weniger, dann den rechten. Ein nach einer solchen Regel konstruierter Baum kann dann leicht umgangen werden, um von Knoten mit niedrigeren Werten zu Knoten mit größeren Werten zu gelangen (und somit alle Elemente in aufsteigender Reihenfolge zu erhalten).
Der Hauptfehler beim Sortieren nach Einfügungen (die Kosten für das Einfügen eines Elements an seiner Stelle im sortierten Teil des Arrays) ist hier gelöst. Die Konstruktion geht recht schnell voran. In jedem Fall ist es zum Freigeben der Einfügemarke nicht erforderlich, die Karawanen der Elemente wie in den vorherigen Algorithmen langsam zu bewegen. Es scheint, dass hier die besten Sortiereinsätze sind. Aber es gibt ein Problem.
Wenn Sie einen schönen symmetrischen Weihnachtsbaum (den sogenannten perfekt ausbalancierten Baum) wie in der Animation drei Absätze oben erhalten, erfolgt das Einfügen schnell, da der Baum in diesem Fall die niedrigstmöglichen Verschachtelungsebenen aufweist. Eine ausgeglichene (oder zumindest nahe daran liegende) Struktur aus einem zufälligen Array wird jedoch selten erhalten. Und der Baum wird höchstwahrscheinlich unvollkommen und unausgeglichen sein - mit Verzerrungen, einem verschmutzten Horizont und einer übermäßigen Anzahl von Ebenen.
Ein zufälliges Array mit Werten von 1 bis 10. Elemente in dieser Reihenfolge erzeugen einen unausgeglichenen Binärbaum: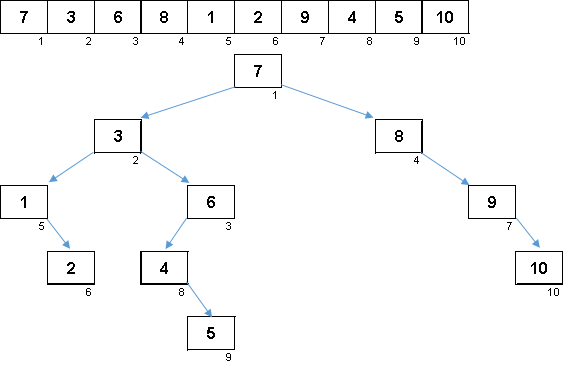
Ein Baum reicht nicht zum Bauen, er muss noch umgangen werden. Je mehr Ungleichgewicht - desto stärker rutscht der Algorithmus für die Baumdurchquerung. Hier kann, wie die Sterne sagen, ein zufälliges Array sowohl einen hässlichen Haken (was wahrscheinlicher ist) als auch ein baumartiges Fraktal erzeugen.
Die Werte der Elemente sind gleich, aber die Reihenfolge ist unterschiedlich. Ein ausgeglichener Binärbaum wird generiert: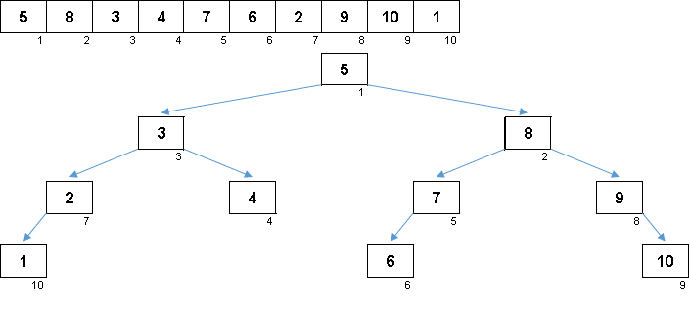
 Auf schöner Sakura
Auf schöner Sakura
Nicht genug Blütenblatt:
Ein binärer Baum von Dutzenden.Das Problem der unausgeglichenen Bäume wird durch Inversionssortierung gelöst, bei der eine spezielle Art von binärem Suchbaum verwendet wird - der Spreizbaum. Dies ist ein wunderbarer Transformatorbaum, der nach jeder Operation in einem ausgeglichenen Zustand wiederhergestellt wird. Darüber wird ein separater Artikel sein. Bis dahin werde ich Python-Implementierungen sowohl für die Baumsortierung als auch für die Splay-Sortierung vorbereiten.
Nun, wir haben kurz die beliebtesten Sortiereinsätze durchgesehen. Einfache Einfügungen, Shell und Binärbaum, die wir alle aus der Schule kennen. Betrachten Sie nun andere Vertreter dieser Klasse, die nicht so bekannt sind.
Wiki / Wiki -
Einfügen , Shell / Shell , Baum / BaumSerienartikel:
Wer AlgoLab verwendet - Ich empfehle, die Datei zu aktualisieren. Ich habe dieser Anwendung einfache binäre Sucheinfügungen und gepaarte Einfügungen hinzugefügt. Er hat auch die Visualisierung für Shell komplett neu geschrieben (in der vorherigen Version gab es nichts zu verstehen) und dem übergeordneten Zweig beim Einfügen eines Elements in den Binärbaum Hervorhebungen hinzugefügt.