Neuronale Netze, grundlegende Funktionsprinzipien, Vielfalt und Topologie

Neuronale Netze haben das Gebiet der Mustererkennung revolutioniert, werden jedoch aufgrund der nicht offensichtlichen Interpretierbarkeit des Funktionsprinzips nicht in Bereichen wie Medizin und Risikobewertung eingesetzt. Es erfordert eine visuelle Darstellung des Netzwerks, wodurch es keine Black Box, sondern zumindest „durchscheinend“ wird. Cristopher Olah demonstrierte in Neuronale Netze, Mannigfaltigkeiten und Topologie die Prinzipien des neuronalen Netzbetriebs und verband sie mit der mathematischen Theorie der Topologie und Diversität, die als Grundlage für diesen Artikel diente. Um den Betrieb eines neuronalen Netzwerks zu demonstrieren, werden niedrigdimensionale tiefe neuronale Netzwerke verwendet.

Das Verständnis des Verhaltens tiefer neuronaler Netze ist im Allgemeinen keine triviale Aufgabe. Es ist einfacher, niedrigdimensionale tiefe neuronale Netze zu erforschen - Netze, in denen sich nur wenige Neuronen in jeder Schicht befinden. Für niedrigdimensionale Netzwerke können Sie Visualisierungen erstellen, um das Verhalten und das Training solcher Netzwerke zu verstehen. Diese Perspektive wird ein tieferes Verständnis des Verhaltens neuronaler Netze vermitteln und die Verbindung beobachten, die neuronale Netze mit einem Feld der Mathematik kombiniert, das als Topologie bezeichnet wird.

Daraus ergeben sich eine Reihe interessanter Dinge, einschließlich der grundlegenden Untergrenzen für die Komplexität eines neuronalen Netzwerks, das bestimmte Datensätze klassifizieren kann.

Betrachten Sie das Prinzip des Netzwerks anhand eines Beispiels

Beginnen wir mit einem einfachen Datensatz - zwei Kurven in einer Ebene. Die Netzwerkaufgabe lernt, die zu Kurven gehörenden Punkte zu klassifizieren.



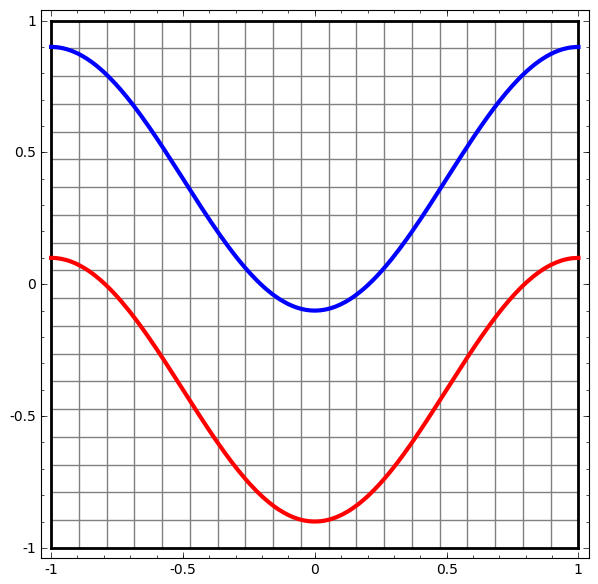
Eine naheliegende Möglichkeit, das Verhalten eines neuronalen Netzwerks zu visualisieren und zu sehen, wie der Algorithmus alle möglichen Objekte (in unserem Beispiel Punkte) aus einem Datensatz klassifiziert.

Beginnen wir mit der einfachsten Klasse neuronaler Netze mit einer Eingabe- und Ausgabeschicht. Ein solches Netzwerk versucht, zwei Datenklassen zu trennen, indem es sie durch eine Linie teilt.



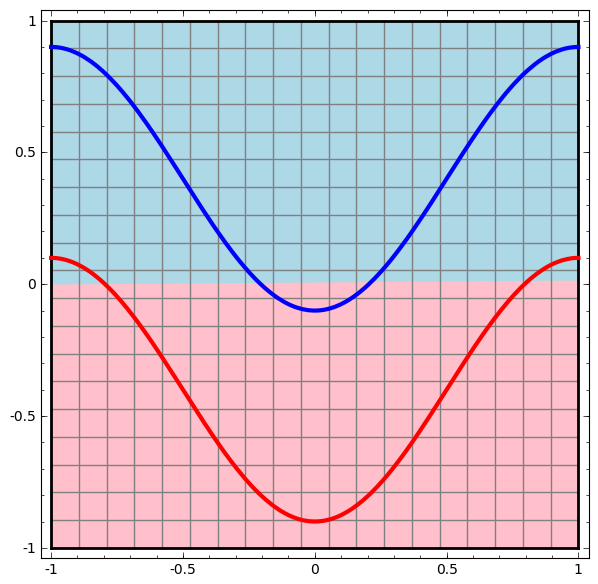
Ein solches Netzwerk wird in der Praxis nicht verwendet. Moderne neuronale Netze haben normalerweise mehrere Schichten zwischen ihrer Eingabe und Ausgabe, die als "versteckte" Schichten bezeichnet werden.

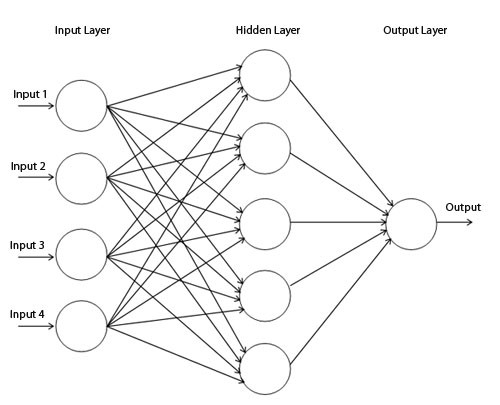
Einfaches Netzwerkdiagramm

Wir visualisieren das Verhalten dieses Netzwerks und beobachten, was es mit verschiedenen Punkten in seinem Bereich macht. Ein Hidden-Layer-Netzwerk trennt Daten von einer komplexeren Kurve als eine Linie.



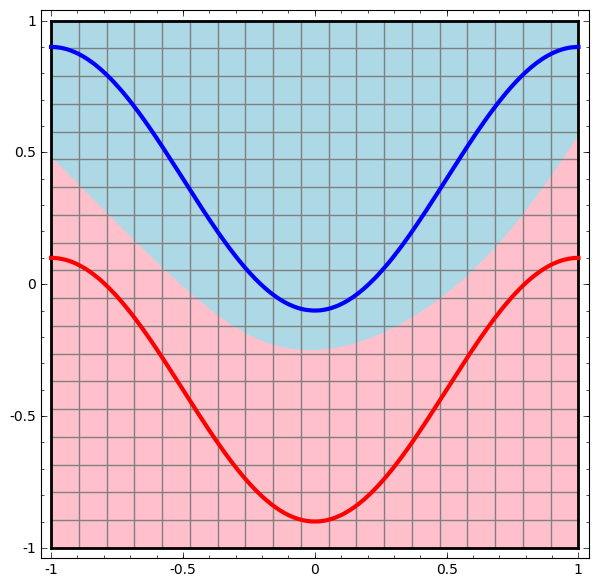
Mit jeder Schicht transformiert das Netzwerk die Daten und erstellt eine neue Ansicht. Wir können die Daten in jeder dieser Ansichten sehen und wie das Netzwerk mit einer verborgenen Schicht sie klassifiziert. Wenn der Algorithmus die endgültige Präsentation erreicht, zieht das neuronale Netzwerk eine Linie durch die Daten (oder in höheren Dimensionen - eine Hyperebene).

In der vorherigen Visualisierung werden die Daten in einer Rohansicht berücksichtigt. Sie können sich das vorstellen, indem Sie sich die Eingabeebene ansehen. Betrachten Sie es nun, nachdem es in die erste Ebene konvertiert wurde. Sie können sich das vorstellen, indem Sie die verborgene Ebene betrachten.
Jede Messung entspricht der Aktivierung eines Neurons in der Schicht.



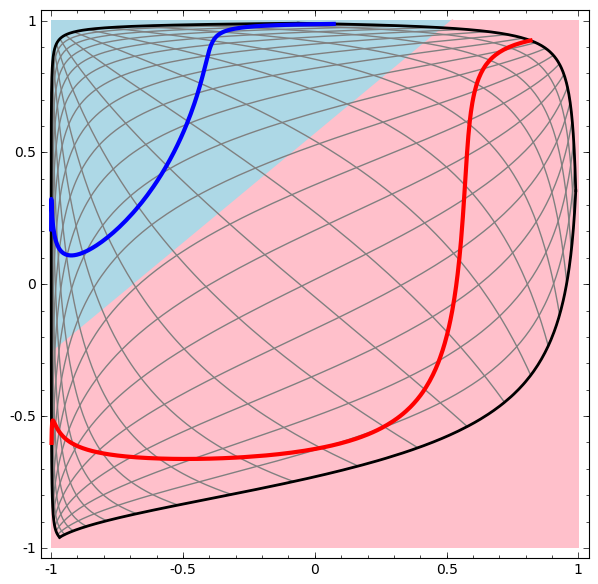
Die verborgene Ebene wird in der Ansicht so trainiert, dass die Daten linear trennbar sind.

Kontinuierliches Layer-Rendering

In dem im vorherigen Abschnitt beschriebenen Ansatz lernen wir, Netzwerke zu verstehen, indem wir uns die Präsentation ansehen, die jeder Schicht entspricht. Dies gibt uns eine diskrete Liste von Ansichten.

Der nicht triviale Teil ist zu verstehen, wie wir uns von einem zum anderen bewegen. Glücklicherweise haben neuronale Netzwerkebenen Eigenschaften, die dies ermöglichen.
Es gibt viele verschiedene Arten von Schichten, die in neuronalen Netzen verwendet werden.

Betrachten Sie eine Tanh-Schicht für ein bestimmtes Beispiel. Die Tanh-Tanh-Schicht (Wx + b) besteht aus:

1. Die lineare Transformation der "Gewichts" -Matrix W.
2. Übersetzung mit Vektor b
3. Spot Anwendung von Tanh.

Wir können dies als kontinuierliche Transformation wie folgt darstellen:



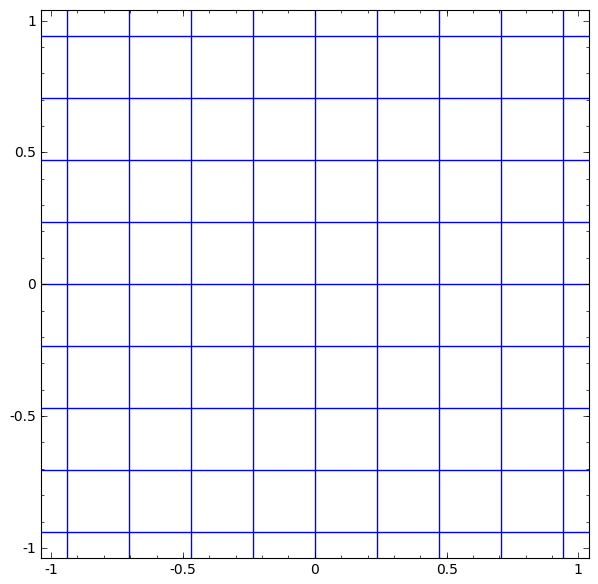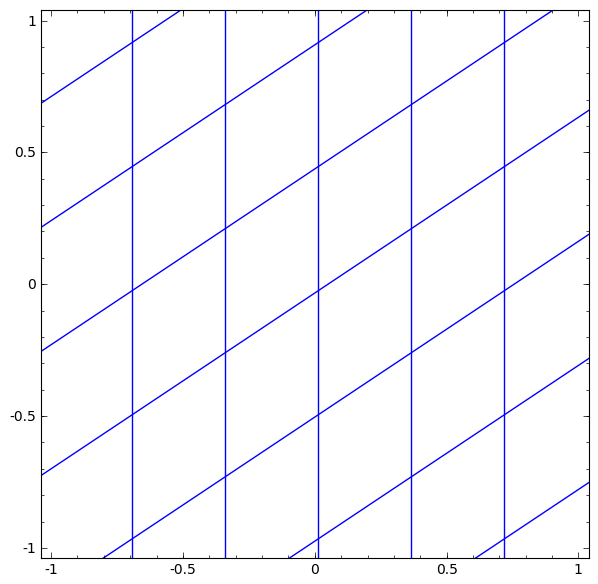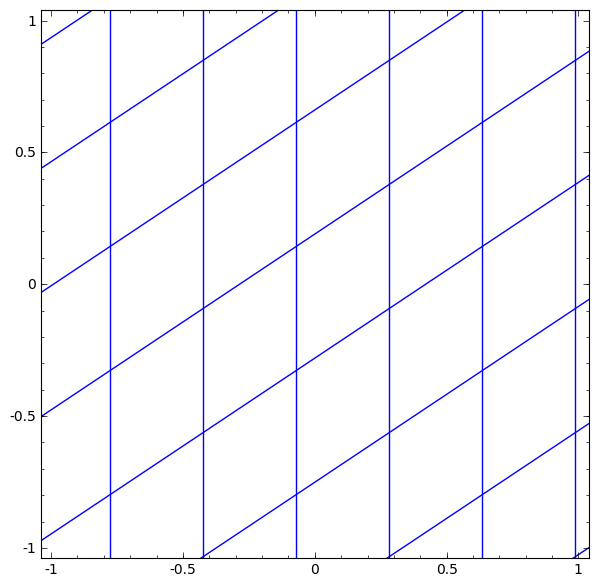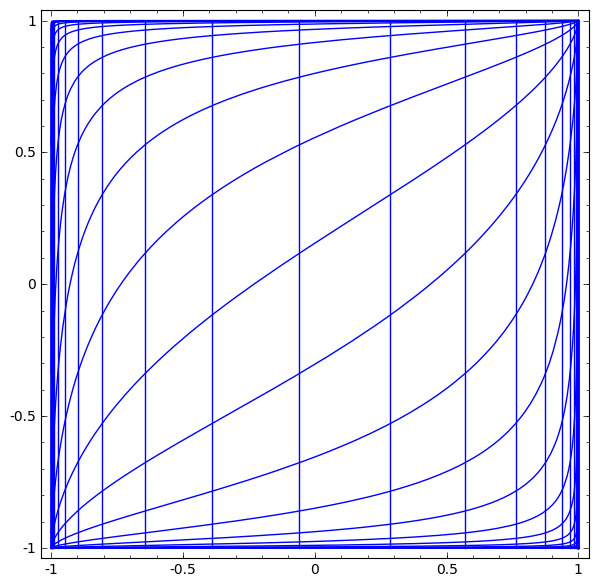
Dieses Funktionsprinzip ist anderen Standardschichten sehr ähnlich, die aus einer affinen Transformation bestehen, gefolgt von der punktweisen Anwendung einer monotonen Aktivierungsfunktion.
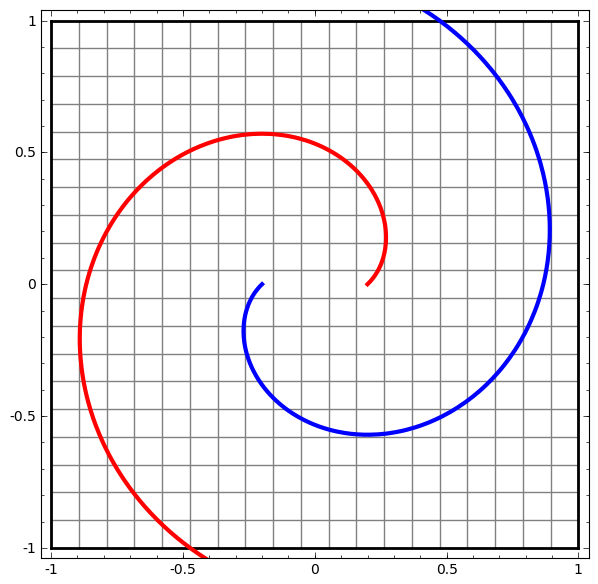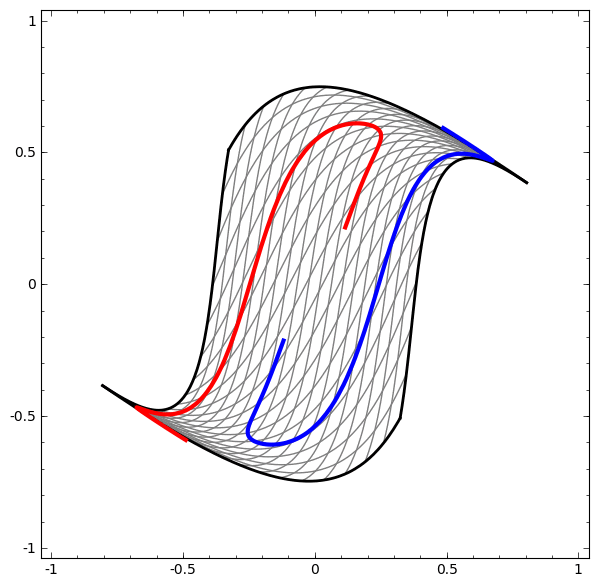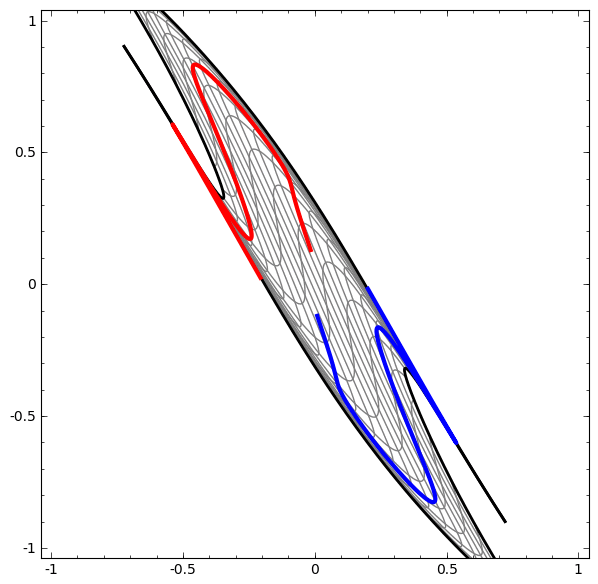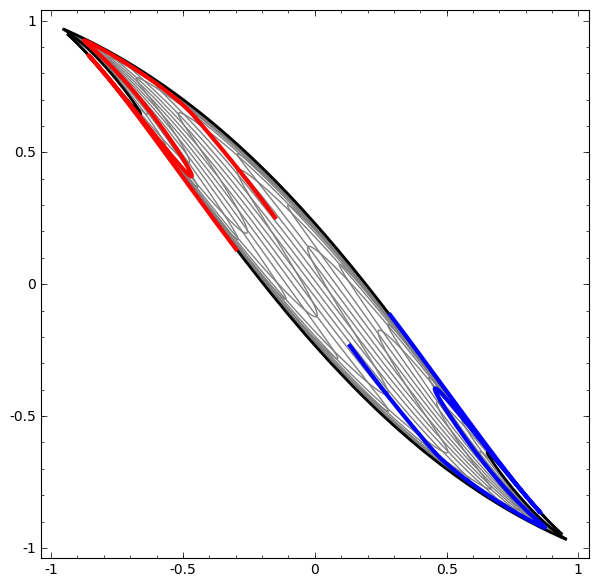
Diese Methode kann verwendet werden, um komplexere Netzwerke zu verstehen. Das folgende Netzwerk klassifiziert also zwei Spiralen, die sich mithilfe von vier verborgenen Schichten leicht verheddern. Im Laufe der Zeit ist ersichtlich, dass sich das neuronale Netzwerk von einer Rohansicht auf eine höhere Ebene bewegt, die das Netzwerk zur Klassifizierung von Daten untersucht hat. Während sich die Spiralen anfänglich verheddern, sind sie gegen Ende linear trennbar.



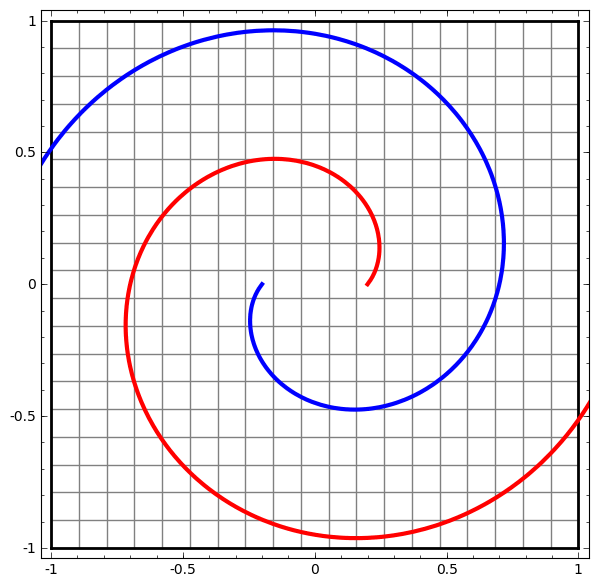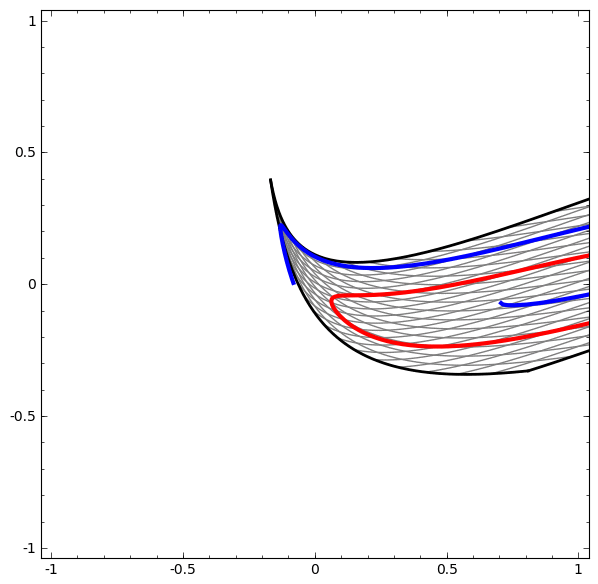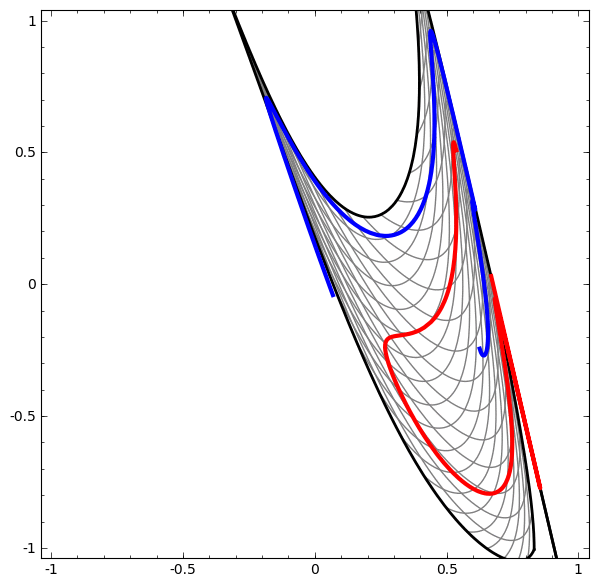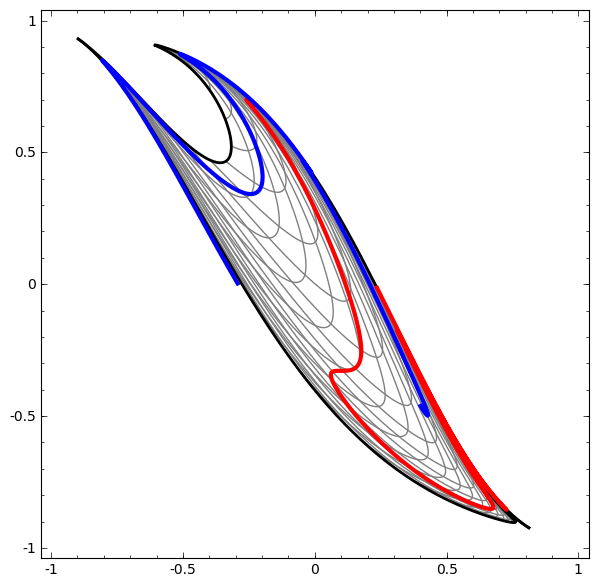
Auf der anderen Seite das nächste Netzwerk, das ebenfalls mehrere Ebenen verwendet, aber nicht zwei Spiralen klassifizieren kann, die sich mehr verwickeln.



Es ist zu beachten, dass diese Aufgaben eine begrenzte Komplexität aufweisen, da niedrigdimensionale neuronale Netze verwendet werden. Wenn breitere Netzwerke verwendet wurden, wurde die Problemlösung vereinfacht.

Tang-Schichten

Jede Schicht streckt und komprimiert den Raum, schneidet aber nie, bricht nicht und faltet ihn nicht. Intuitiv sehen wir, dass die topologischen Eigenschaften auf jeder Schicht erhalten bleiben.

Solche Transformationen, die die Topologie nicht beeinflussen, werden als Homomorphismen bezeichnet (Wiki - Dies ist eine Abbildung des algebraischen Systems A, bei der die grundlegenden Operationen und grundlegenden Beziehungen erhalten bleiben). Formal sind sie Bijektionen, die kontinuierliche Funktionen in beide Richtungen sind. Bei einer bijektiven Zuordnung entspricht jedes Element einer Menge genau einem Element einer anderen Menge, und eine inverse Zuordnung mit derselben Eigenschaft wird definiert.

Der Satz

Schichten mit N Eingängen und N Ausgängen sind Homomorphismen, wenn die Gewichtsmatrix W nicht entartet ist. (Sie müssen vorsichtig mit der Domain und dem Bereich sein.)

Topologie und Klassifizierung

Betrachten Sie einen zweidimensionalen Datensatz mit zwei Klassen A, B⊂R2:

A = {x | d (x, 0) <1/3}

B = {x | 2/3 <d (x, 0) <1}



A rot, B blau

Voraussetzung: Ein neuronales Netzwerk kann diesen Datensatz unabhängig von der Breite nicht ohne drei oder mehr versteckte Ebenen klassifizieren.

Wie bereits erwähnt, entspricht die Klassifizierung mit einer Sigmoidfunktion oder einer Softmax-Schicht dem Versuch, die Hyperebene (oder in diesem Fall die Linie) zu finden, die A und B in der endgültigen Darstellung trennt. Mit nur zwei versteckten Schichten kann das Netzwerk Daten auf diese Weise topologisch nicht gemeinsam nutzen und ist zum Scheitern in diesem Datensatz verurteilt.
In der nächsten Visualisierung beobachten wir eine latente Ansicht, während das Netzwerk zusammen mit der Klassifizierungslinie trainiert.



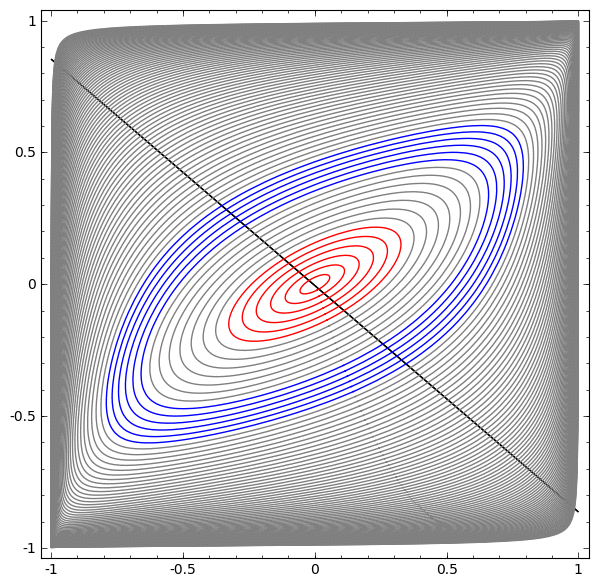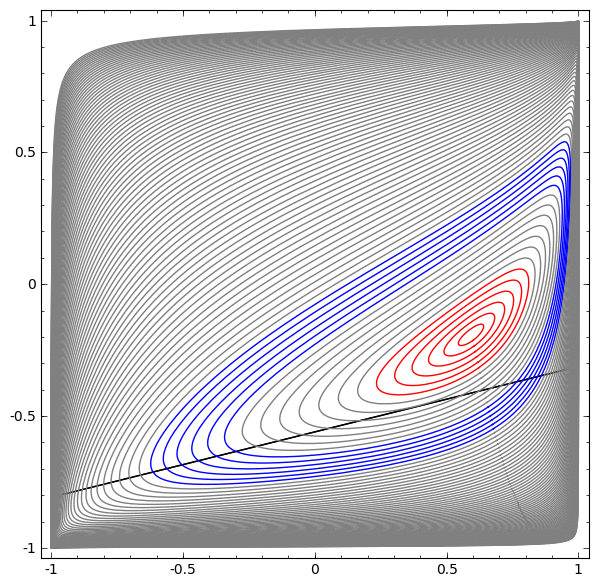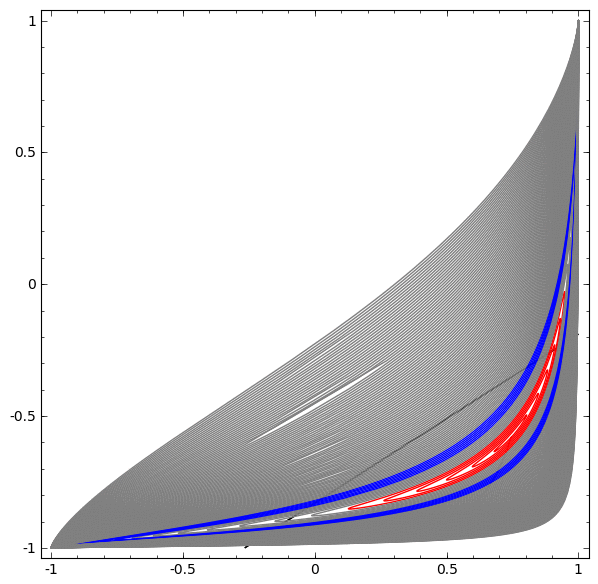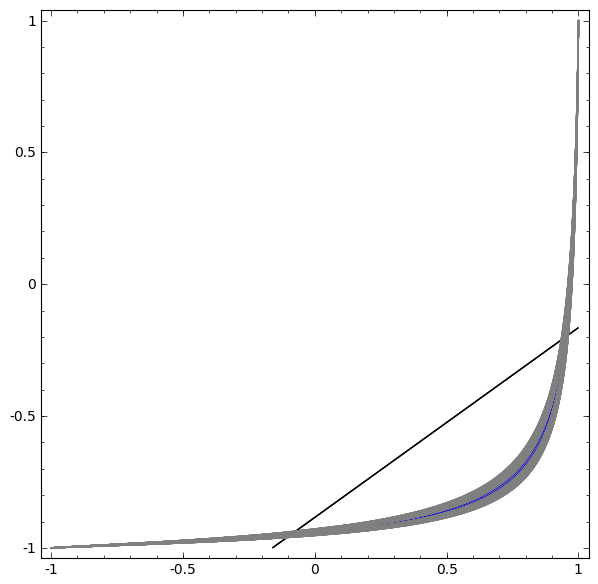
Denn dieses Trainingsnetz reicht nicht aus, um ein hundertprozentiges Ergebnis zu erzielen.
Der Algorithmus fällt in ein unproduktives lokales Minimum, kann jedoch eine Klassifizierungsgenauigkeit von ~ 80% erreichen.

In diesem Beispiel gab es nur eine verborgene Ebene, die jedoch nicht funktionierte.
Aussage. Entweder ist jede Schicht ein Homomorphismus oder die Gewichtsmatrix der Schicht hat die Determinante 0.


Wenn wir ein drittes verstecktes Element hinzufügen, wird das Problem trivial. Das neuronale Netzwerk erkennt die folgende Darstellung:



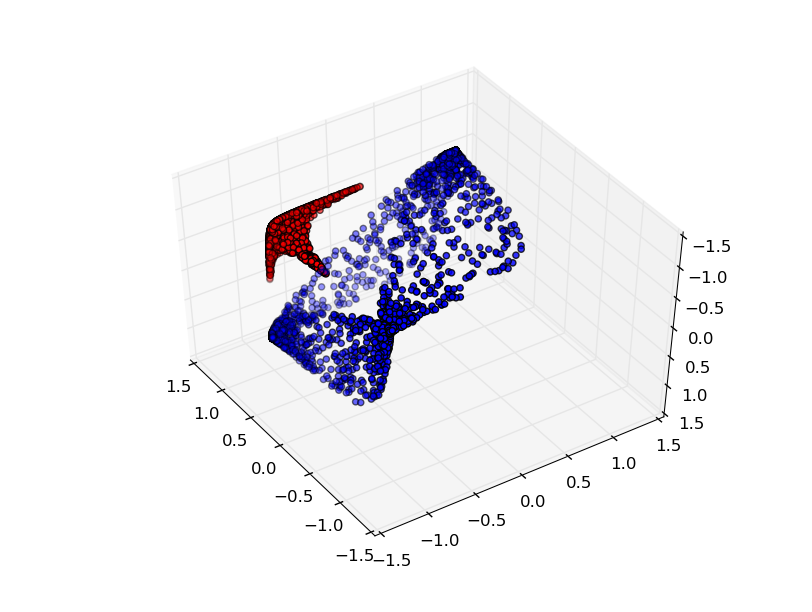
Die Ansicht ermöglicht es, Datensätze mit einer Hyperebene zu trennen.
Um besser zu verstehen, was los ist, schauen wir uns einen noch einfacheren Datensatz an, der eindimensional ist:



A = [- 1 / 3,1 / 3]
B = [- 1, –2 / 3] ∪ [2 / 3,1]
Ohne die Verwendung einer Ebene aus zwei oder mehr versteckten Elementen können wir diesen Datensatz nicht klassifizieren. Wenn wir jedoch ein Netzwerk mit zwei Elementen verwenden, lernen wir, wie die Daten als gute Kurve dargestellt werden, mit der wir Klassen mithilfe einer Linie trennen können:



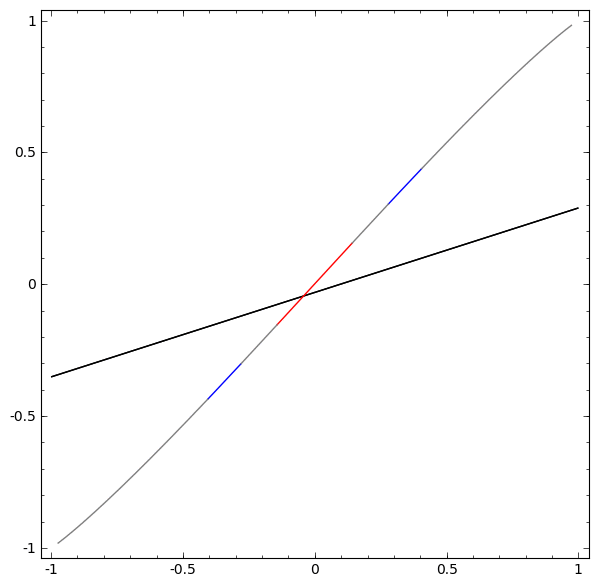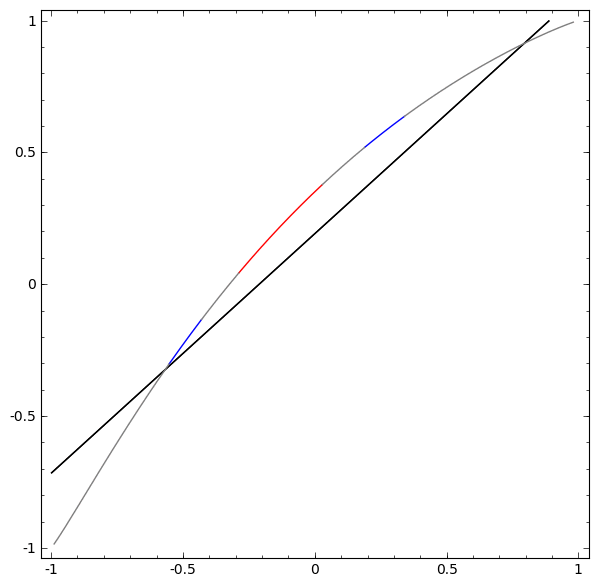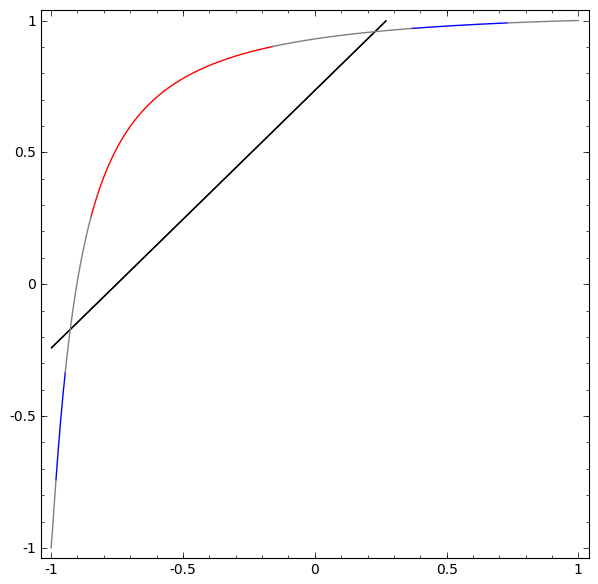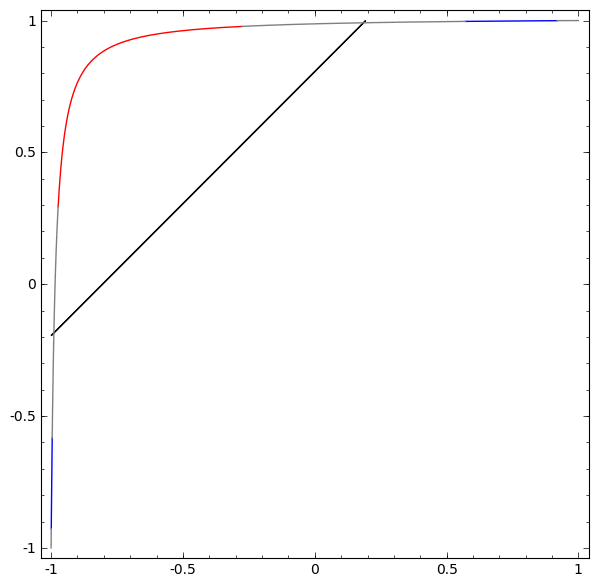
Was ist los? Ein verstecktes Element lernt zu feuern, wenn x> -1/2, und eines lernt zu feuern, wenn x> 1/2. Wenn der erste ausgelöst wird, aber nicht der zweite, wissen wir, dass wir uns in A befinden.

Sortenvermutung

Gilt dies für Datensätze aus der realen Welt, z. B. Bildsätze? Wenn Sie die Diversitätshypothese ernst nehmen, denke ich, dass es wichtig ist.

Die mehrdimensionale Hypothese lautet, dass natürliche Daten im Implantationsraum niedrigdimensionale Mannigfaltigkeiten bilden. Es gibt sowohl theoretische [1] als auch experimentelle [2] Gründe zu der Annahme, dass dies wahr ist. Wenn ja, besteht die Aufgabe des Klassifizierungsalgorithmus darin, das Bündel verschränkter Verteiler zu trennen.

In den vorherigen Beispielen hat eine Klasse die andere vollständig umgeben. Es ist jedoch unwahrscheinlich, dass die Vielfalt der Hundebilder vollständig von einer Sammlung von Katzenbildern umgeben ist. Es gibt jedoch noch andere, plausibelere topologische Situationen, die möglicherweise noch auftreten, wie wir im nächsten Abschnitt sehen werden.

Verbindungen und Homotopien

Ein weiterer interessanter Datensatz sind die beiden verbundenen Tori A und B.



Wie die vorherigen Datensätze, die wir untersucht haben, kann dieser Datensatz nicht ohne Verwendung von n + 1 Dimensionen, nämlich der vierten Dimension, geteilt werden.

Verbindungen werden in der Knotentheorie auf dem Gebiet der Topologie untersucht. Manchmal, wenn wir einen Zusammenhang sehen, ist nicht sofort klar, ob es sich um Inkohärenz handelt (viele Dinge, die sich verheddern, aber durch kontinuierliche Verformung getrennt werden können) oder nicht.



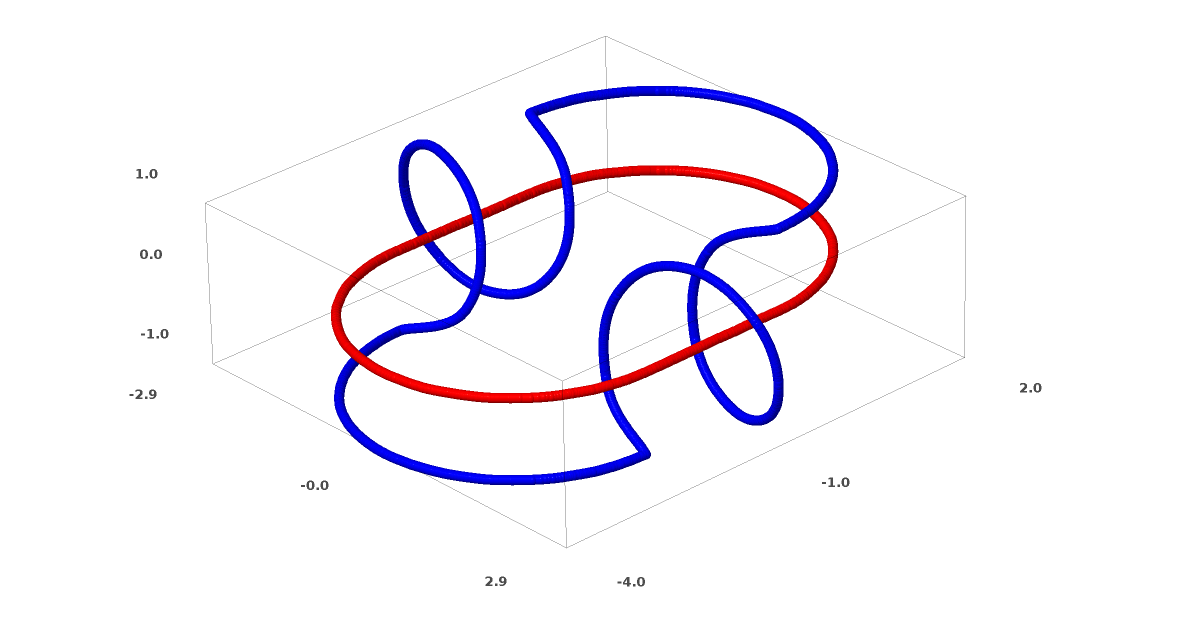
Relativ einfache Inkohärenz.

Wenn ein neuronales Netzwerk, das Schichten mit nur drei Einheiten verwendet, es klassifizieren kann, ist es inkohärent. (Frage: Können theoretisch alle Inkohärenzen mit nur drei Inkohärenzen über das Netzwerk klassifiziert werden?)

Aus Sicht dieses Knotens ist die kontinuierliche Visualisierung von Darstellungen, die von einem neuronalen Netzwerk erstellt wurden, ein Verfahren zum Auflösen von Verbindungen. In der Topologie nennen wir diese Umgebungsisotopie zwischen der ursprünglichen Verbindung und den getrennten.

Formal ist die Isotopie des umgebenden Raums zwischen den Mannigfaltigkeiten A und B eine stetige Funktion F: [0,1] × X → Y, so dass jedes Ft ein Homöomorphismus von X zu seinem Bereich ist, F0 eine Identitätsfunktion ist und F1 A auf B abbildet. T. .e. Ft geht kontinuierlich von der Karte A zu sich selbst, zur Karte A nach B.

Satz: Es gibt eine Isotopie des umgebenden Raums zwischen dem Eingang und der Darstellung der Netzwerkebene, wenn: a) W nicht entartet ist, b) wir bereit sind, Neuronen auf die verborgene Schicht zu übertragen, und c) es mehr als ein verborgenes Element gibt.


Bisher ist es unwahrscheinlich, dass die Beziehungen, von denen wir gesprochen haben, in realen Daten auftreten, aber es gibt Verallgemeinerungen auf einer höheren Ebene. Es ist plausibel, dass solche Merkmale in realen Daten vorhanden sein können.

Verbindungen und Knoten sind eindimensionale Mannigfaltigkeiten, aber wir benötigen vier Dimensionen, damit die Netzwerke alle entwirren können. In ähnlicher Weise kann ein noch höherdimensionaler Raum erforderlich sein, um n-dimensionale Mannigfaltigkeiten erweitern zu können. Alle n-dimensionalen Verteiler können in 2n + 2 Dimensionen erweitert werden. [3]

Einfacher Ausstieg

Der einfache Weg ist, zu versuchen, die Verteiler auseinander zu ziehen und die Teile zu dehnen, die sich so verwickeln wie möglich. Obwohl dies einer echten Lösung nicht nahe kommt, kann eine solche Lösung eine relativ hohe Klassifizierungsgenauigkeit erreichen und ein akzeptables lokales Minimum darstellen.



Solche lokalen Minima sind absolut nutzlos, um topologische Probleme zu lösen, aber topologische Probleme können eine gute Motivation für die Untersuchung dieser Probleme darstellen.

Wenn wir dagegen nur an guten Klassifizierungsergebnissen interessiert sind, ist der Ansatz akzeptabel. Wenn ein winziger Teil eines Datenverteilers in einem anderen Verteiler erfasst wird, ist dies ein Problem? Es ist wahrscheinlich, dass es trotz dieses Problems möglich sein wird, beliebig gute Klassifizierungsergebnisse zu erhalten.

Verbesserte Schichten zur Manipulation von Verteilern?

Es ist schwer vorstellbar, dass Standardschichten mit affinen Transformationen wirklich gut zur Manipulation von Mannigfaltigkeiten geeignet sind.

Vielleicht ist es sinnvoll, eine völlig andere Schicht zu haben, die wir in der Komposition mit traditionelleren verwenden können?

Die Untersuchung eines Vektorfeldes mit einer Richtung, in die wir die Mannigfaltigkeit verschieben wollen, ist vielversprechend:



Und dann verformen wir den Raum basierend auf dem Vektorfeld:



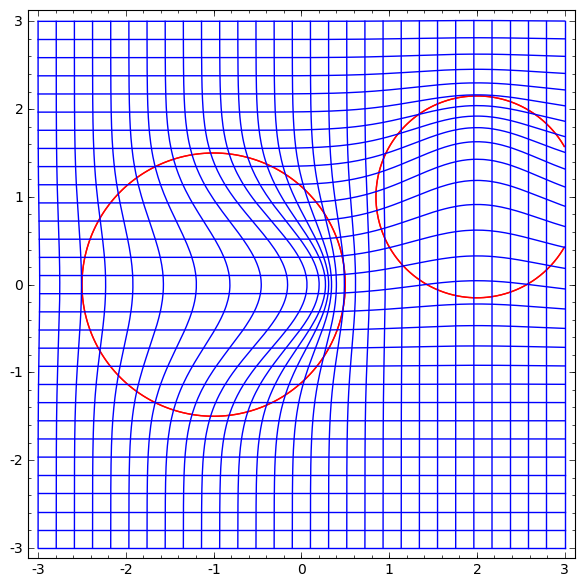
Man könnte das Vektorfeld an festen Punkten untersuchen (einfach einige feste Punkte aus dem Testdatensatz zur Verwendung als Anker nehmen) und irgendwie interpolieren.


Wobei v0 und v1 Vektoren sind und f0 (x) und f1 (x) n-dimensionale Gaußsche sind.

K-Nearest Neighbor Layers

Die lineare Trennbarkeit kann ein großer und möglicherweise unangemessener Bedarf an neuronalen Netzen sein. Es ist natürlich, die Methode der k-nächsten Nachbarn (k-NN) zu verwenden. Der Erfolg von k-NN hängt jedoch stark von der Präsentation ab, die es klassifiziert. Daher ist eine gute Präsentation erforderlich, bevor das k-NN gut funktionieren kann.

k-NN ist in Bezug auf die Darstellung, auf die es einwirkt, differenzierbar. Auf diese Weise können wir das Netzwerk direkt trainieren, um k-NN zu klassifizieren. Dies kann als eine Art "nächster Nachbar" -Schicht angesehen werden, die als Alternative zu Softmax fungiert.
Wir möchten nicht mit unserem gesamten Training für jede Mini-Party warnen, da dies ein sehr teures Verfahren sein wird. Der angepasste Ansatz besteht darin, jedes Element des Mini-Loses basierend auf den Klassen der anderen Elemente des Mini-Loses zu klassifizieren, wobei jedes Einheitsgewicht geteilt durch den Abstand vom Klassifizierungsziel angegeben wird.

Leider verringert die Verwendung von k-NN selbst bei komplexen Architekturen die Fehlerwahrscheinlichkeit - und die Verwendung einfacherer Architekturen verschlechtert die Ergebnisse.

Fazit

Topologische Eigenschaften von Daten, wie z. B. Beziehungen, können die lineare Aufteilung von Klassen mithilfe niedrigdimensionaler Netzwerke unabhängig von der Tiefe unmöglich machen. Auch in Fällen, in denen dies technisch möglich ist. Zum Beispiel Spiralen, deren Trennung sehr schwierig sein kann.

Für eine genaue Datenklassifizierung benötigen neuronale Netze breite Schichten. Darüber hinaus sind die traditionellen Schichten des neuronalen Netzwerks schlecht geeignet, um wichtige Manipulationen mit Mannigfaltigkeiten darzustellen. Selbst wenn wir die Gewichte manuell einstellen, wäre es schwierig, die gewünschten Transformationen kompakt darzustellen.