Lerne OpenGL. Lektion 5.6 - Parallaxenzuordnung

Parallaxenabbildung

Die Parallax Mapping- Texturierungstechnik ähnelt in ihrer Wirkung der normalen Zuordnung , basiert jedoch auf einem anderen Prinzip. Die Ähnlichkeit besteht darin, dass diese Technik wie das normale Mapping die visuelle Komplexität und Detailgenauigkeit der Oberfläche mit der angewendeten Textur erheblich erhöht und gleichzeitig eine plausible Illusion des Vorhandenseins von Höhenunterschieden auf der Oberfläche erzeugt. Parallax Mapping funktioniert hervorragend in Verbindung mit Normal Mapping, um sehr zuverlässige Ergebnisse zu erzielen: Die beschriebene Technik vermittelt den Reliefeffekt viel besser als Normal Mapping, und Normal Mapping ergänzt ihn für eine plausible Simulation dynamischer Beleuchtung. Parallax Mapping kann kaum als eine Technik angesehen werden, die in direktem Zusammenhang mit Beleuchtungssimulationsmethoden steht. Dennoch habe ich diesen Abschnitt ausgewählt, um dies zu berücksichtigen, da die Methode eine logische Weiterentwicklung der Ideen des normalen Mappings ist. Ich stelle auch fest, dass zum Parsen dieses Artikels ein gutes Verständnis des Normal Mapping-Algorithmus erforderlich ist, insbesondere des Konzepts des Tangentenraums oder des Tangentenraums .


Die Parallaxenzuordnung gehört zur Familie der Verschiebungszuordnungen oder geprägten Texturierungstechniken, mit denen die Eckpunkte einer Geometrie basierend auf Werten versetzt werden, die in speziellen Texturabbildungen gespeichert sind. Stellen Sie sich zum Beispiel eine Ebene vor, die aus der Größenordnung von tausend Eckpunkten besteht. Jeder von ihnen kann entsprechend dem aus der Textur gelesenen Wert verschoben werden, der die Höhe der Ebene an einem bestimmten Punkt darstellt. Eine solche Textur, die die Höhenwerte in jedem Texel enthält, wird als Höhenkarte bezeichnet . Ein Beispiel für eine solche Karte, die auf der Grundlage der geometrischen Eigenschaften der Oberfläche des Mauerwerks erhalten wurde, ist das folgende Bild:


Durch Abtasten aus dieser Karte und Verschieben jedes Scheitelpunkts gemäß dem Höhenwert ist es möglich, eine konvexe Oberfläche aus einer idealen Ebene zu erhalten, die die geometrischen Parameter der ursprünglichen Oberfläche wiederholt. Wenn Sie also eine Ebene mit einer ausreichenden Anzahl von Scheitelpunkten nehmen und eine Höhenkarte aus dem Beispiel anwenden, erhalten Sie das folgende Ergebnis:


Der beschriebene Ansatz ist einfach und leicht zu implementieren, erfordert jedoch eine hohe Dichte an Eckpunkten im verarbeiteten Objekt, da sonst das Ergebnis der Verschiebung zu grob ist. Und wenn wir auf jeder ebenen Fläche tausend oder mehr Eckpunkte freigeben, haben wir sehr bald einfach keine Zeit mehr, alles zu rendern, was wir brauchen. Vielleicht gibt es einen Algorithmus, mit dem Sie die Qualität des naiven Displacement Mapping-Algorithmus qualitativ simulieren können, ohne jedoch solche Geometriekosten zu verursachen? Wenn Sie stehen, setzen Sie sich, denn im Bild oben gibt es tatsächlich nur sechs Eckpunkte (zwei Dreiecke)! Das Relief des Mauerwerks wird dank der Verwendung von Parallax Mapping perfekt nachgeahmt, einer Relief-Texturierungstechnik, die nicht viele Eckpunkte erfordert, um das Oberflächenrelief originalgetreu zu vermitteln, sondern wie Normal Mapping einen originellen Ansatz verwendet, um die Augen des Betrachters zu täuschen.

Die Hauptidee der Implementierung besteht darin, die Texturkoordinaten für das aktuelle Fragment basierend auf der Blickrichtung und den Höhenkartendaten zu verzerren, um die Illusion zu erzeugen, dass dieses Fragment zu einem Teil der Oberfläche gehört, der höher oder niedriger liegt als er tatsächlich ist. Schauen Sie sich zum besseren Verständnis des Prinzips das Diagramm unseres Beispiels mit Ziegeln an:

Hier repräsentiert die raue rote Linie die Werte aus der Höhenkarte, die die geometrischen Eigenschaften der simulierten Mauerwerksoberfläche widerspiegeln. Vektor $$$\ color {orange} {\ bar {V}}$ repräsentiert die Richtung von der Oberfläche zum Betrachter ( viewDir ). Wenn das Flugzeug wirklich geprägt wäre, würde der Betrachter einen Punkt auf der Oberfläche sehen $$$\ color {blue} B$ . Tatsächlich haben wir jedoch eine ideale Ebene und der Strahl in Blickrichtung kreuzt die Ebene an einem Punkt $$$\ color {green} A$ das ist offensichtlich. Parallaxen-Mapping-Aufgabe zum Verschieben von Texturkoordinaten an einem Punkt $$$\ color {green} A$ so dass sie mit den dem Punkt entsprechenden Koordinaten identisch werden $$$\ color {blue} B$ . Weiter für das aktuelle Fragment (entspricht dem Punkt $$$\ color {green} A$ ) Wir verwenden die erhaltenen Koordinaten des Punktes $$$\ color {blue} B$ Texturabtastung ist für alle notwendig, was die Illusion erzeugt, dass der Betrachter einen Punkt sieht $$$\ color {blue} B$ .

Die Hauptschwierigkeit liegt in der Berechnung der Texturkoordinaten eines Punktes $$$\ color {blue} B$ am Punkt sein $$$\ color {green} A$ . Parallax Mapping bietet eine ungefähre Lösung durch einfache Skalierung des Richtungsvektors von der Oberfläche $$$\ color {orange} {\ bar {V}}$ an den Betrachter durch die Höhe des Fragments $$$\ color {green} A$ . Das heißt, ändere einfach die Länge $$$\ color {orange} {\ bar {V}}$ so dass es mit der Stichprobengröße aus der Höhenkarte übereinstimmt $$$\ color {green} {H (A)}$ entsprechend dem Fragment $$$\ color {green} A$ . Das folgende Diagramm zeigt das Ergebnis des Skalierungsvektors $$$\ color {brown} {\ bar {P}}$ ::


Als nächstes der resultierende Vektor $$$\ color {brown} {\ bar {P}}$ zerlegt in Komponenten gemäß dem Koordinatensystem der Ebene selbst, die als Offsets für die ursprünglichen Texturkoordinaten verwendet werden. Darüber hinaus ist da der Vektor $$$\ color {brown} {\ bar {P}}$ wird anhand des Werts aus der Höhenkarte berechnet. Je mehr der Höhenwert dem aktuellen Fragment entspricht, desto stärker ist der Versatz dafür.

Diese einfache Technik liefert in einigen Fällen gute Ergebnisse, ist jedoch immer noch eine sehr grobe Schätzung der Position eines Punktes $$$\ color {blue} B$ . Wenn die Höhenkarte Bereiche mit sich stark ändernden Werten enthält, wird das Ergebnis der Verschiebung falsch: höchstwahrscheinlich der Vektor $$$\ color {brown} {\ bar {P}}$ Selbst in der Nähe fällt nicht in die Nähe des Punktes $$$\ color {blue} B$ ::

Basierend auf dem oben Gesagten bleibt eine andere Frage: Wie kann man bestimmen, wie ein Vektor korrekt projiziert wird? $$$\ color {brown} {\ bar {P}}$ zu einer willkürlich ausgerichteten Oberfläche, um Komponenten dazu zu bringen, Texturkoordinaten zu versetzen? Es wäre schön, Berechnungen in einem bestimmten Koordinatensystem durchzuführen, in dem sich der Vektor ausdehnt $$$\ color {brown} {\ bar {P}}$ auf den Komponenten würden x und y immer der Basis des Texturkoordinatensystems entsprechen. Wenn Sie die Lektion über normales Mapping sorgfältig ausgearbeitet haben, haben Sie bereits vermutet, dass es sich um Berechnungen im Tangentenraum handelt.

Übertragen des Vektors von der Oberfläche zum Beobachter $$$\ color {orange} {\ bar {V}}$ in den Tangentenraum erhalten wir einen modifizierten Vektor $$$\ color {brown} {\ bar {P}}$ , deren Komponentenzerlegung immer in Übereinstimmung mit den Tangenten- und Bi-Tangentenvektoren für eine gegebene Oberfläche durchgeführt wird. Da die Tangente und die Bi-Tangente immer an den Achsen des Texturkoordinatensystems der Oberfläche ausgerichtet sind, können Sie unabhängig von der Ausrichtung der Oberfläche die x- und y- Komponenten des Vektors sicher verwenden $$$\ color {brown} {\ bar {P}}$ als Offsets für Texturkoordinaten.

Die Theorie reicht jedoch aus, und nachdem wir die Ärmel hochgekrempelt haben, wenden wir uns der sofortigen Umsetzung zu.

Parallaxenabbildung

Für die Implementierung verwenden wir eine einfache Ebene mit Tangenten und Bias-Tangenten, die dafür berechnet wurden. Dies können wir bereits aus der Lektion über die normale Zuordnung tun. Wir weisen Texturebenen eine Reihe von Ebenen zu: diffuse , Normalen und Offsets , von denen jede unter dem entsprechenden Link verfügbar ist. In der Lektion werden wir auch Normal Mapping verwenden, da Parallax Mapping die Illusion einer Oberflächentopographie erzeugt, die leicht unterbrochen werden kann, wenn sich die Beleuchtung nicht entsprechend der Topographie ändert. Da normale Karten häufig auf der Grundlage von Höhenkarten erstellt werden, gewährleistet ihre kombinierte Verwendung die korrekte Verbindung der Beleuchtung unter Berücksichtigung des Geländes.

Sie haben wahrscheinlich bereits bemerkt, dass die im obigen Link gezeigte Verschiebungskarte tatsächlich die Umkehrung der zu Beginn der Lektion gezeigten Karte ist. Die Implementierung von Parallax Mapping wird normalerweise mit solchen Karten durchgeführt, die invers zu Höhenkarten sind - Tiefenkarten . Dies geschieht, weil die Nachahmung der Aussparungen in der Ebene etwas einfacher ist als die Nachahmung der Höhe. Entsprechend dieser Änderung ändert sich auch das Arbeitsschema Parallax Mapping:


Wieder sehen wir bekannte Punkte $$$\ color {green} A$ und $$$\ color {blue} B$ diesmal jedoch der Vektor $$$\ color {brown} {\ bar {P}}$ erhalten durch Subtrahieren des Vektors $$$\ color {orange} {\ bar {V}}$ von Texturkoordinaten an einem Punkt $$$\ color {green} A$ . Tiefen statt Höhen können einfach durch Subtrahieren der Tiefenprobe von der Einheit oder durch Invertieren der Texturfarben in einem beliebigen Bildeditor erhalten werden.

Die Parallaxenzuordnung ist im Fragment-Shader implementiert, da die Höhendaten für jedes Fragment innerhalb des Dreiecks unterschiedlich sind. Der Fragment-Shader-Code erfordert die Berechnung des Vektors vom Fragment zum Beobachter $$$\ color {orange} {\ bar {V}}$ Daher wird es notwendig sein, ihm die Position des Fragments und des Beobachters im Tangentenraum zu vermitteln. Nach den Ergebnissen der Lektion "Normales Mapping" haben wir immer noch den Vertex-Shader in der Hand, der alle diese Vektoren bereits in den Tangentenraum überträgt. Wir werden ihn verwenden:

#version 330 core layout (location = 0) in vec3 aPos; layout (location = 1) in vec3 aNormal; layout (location = 2) in vec2 aTexCoords; layout (location = 3) in vec3 aTangent; layout (location = 4) in vec3 aBitangent; out VS_OUT { vec3 FragPos; vec2 TexCoords; vec3 TangentLightPos; vec3 TangentViewPos; vec3 TangentFragPos; } vs_out; uniform mat4 projection; uniform mat4 view; uniform mat4 model; uniform vec3 lightPos; uniform vec3 viewPos; void main() { gl_Position = projection * view * model * vec4(aPos, 1.0); vs_out.FragPos = vec3(model * vec4(aPos, 1.0)); vs_out.TexCoords = aTexCoords; vec3 T = normalize(mat3(model) * aTangent); vec3 B = normalize(mat3(model) * aBitangent); vec3 N = normalize(mat3(model) * aNormal); mat3 TBN = transpose(mat3(T, B, N)); vs_out.TangentLightPos = TBN * lightPos; vs_out.TangentViewPos = TBN * viewPos; vs_out.TangentFragPos = TBN * vs_out.FragPos; } 

Von den wichtigen Dingen möchte ich nur bemerken, dass es speziell für die Anforderungen der Parallaxenzuordnung erforderlich ist, den positionPoser im Tangentenraum auf den Fragment-Shader aPos zu übertragen .

Im Shader implementieren wir den Parallax Mapping-Algorithmus, der ungefähr so ​​aussieht:

 #version 330 core out vec4 FragColor; in VS_OUT { vec3 FragPos; vec2 TexCoords; vec3 TangentLightPos; vec3 TangentViewPos; vec3 TangentFragPos; } fs_in; uniform sampler2D diffuseMap; uniform sampler2D normalMap; uniform sampler2D depthMap; uniform float height_scale; vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir); void main() { vec3 viewDir = normalize(fs_in.TangentViewPos - fs_in.TangentFragPos); //       Parallax Mapping vec2 texCoords = ParallaxMapping(fs_in.TexCoords, viewDir); //      //     vec3 diffuse = texture(diffuseMap, texCoords); vec3 normal = texture(normalMap, texCoords); normal = normalize(normal * 2.0 - 1.0); //  –     [...] } 

Wir haben die ParallaxMapping-Funktion angekündigt, die die Texturkoordinaten des Fragments und des Vektors vom Fragment zum Beobachter überträgt $$$\ color {orange} {\ bar {V}}$ im tangentialen Raum. Das Ergebnis der Funktion sind versetzte Texturkoordinaten, die bereits für Samples aus einer diffusen Textur und einer normalen Karte verwendet werden. Infolgedessen entsprechen die diffuse Farbe des Pixels und seine Normalen korrekt der geänderten „Geometrie“ der Ebene.

Was versteckt sich in der ParallaxMapping-Funktion?

  vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir) { float height = texture(depthMap, texCoords).r; vec2 p = viewDir.xy / viewDir.z * (height * height_scale); return texCoords - p; } 

Diese relativ einfache Funktion ist eine wörtliche Implementierung der Methode, deren Hauptpunkte wir oben besprochen haben. TexCoords anfängliche Texturkoordinaten werden genommen , mit deren Hilfe die Höhe (oder Tiefe) ausgewählt wird $$$\ color {green} {H (A)}$ from depthMap für das aktuelle Fragment. Den Vektor berechnen $$$\ color {brown} {\ bar {P}}$ Der viewDir- Vektor wird im Tangentenraum aufgenommen und das Paar seiner x- und y- Komponenten wird durch die z- Komponente geteilt, und das Ergebnis wird durch den Leseversatzwert der Höhe skaliert. Die height_scale- Uniform wurde ebenfalls eingeführt, um eine zusätzliche Kontrolle über den Schweregrad des Parallax Mapping-Effekts zu ermöglichen, da der Verschiebungseffekt normalerweise zu stark ist. Um das Ergebnis zu erhalten, subtrahieren wir den resultierenden Vektor $$$\ color {brown} {\ bar {P}}$ von den ursprünglichen Texturkoordinaten.

Wir werden uns mit dem Moment der Aufteilung von viewDir.xy in viewDir.z befassen . Da der Vektor viewDir normalisiert ist, liegt seine Komponente z im Intervall [0, 1]. Wenn der Vektor nahezu parallel zur Oberfläche der Komponente ist, ist z nahe Null und die Divisionsoperation gibt den Vektor zurück $$$\ color {brown} {\ bar {P}}$ viel länger als wenn viewDir nahe an der Senkrechten zur Oberfläche liegt. Mit anderen Worten, wir skalieren den Vektor $$$\ color {brown} {\ bar {P}}$ so dass es zunimmt, wenn Sie die Oberfläche in einem Winkel betrachten - dies ermöglicht es Ihnen, in solchen Fällen ein realistischeres Ergebnis zu erzielen.

Einige Entwickler ziehen es vor, die Skalierung durch Teilen durch viewDir.z zu entfernen, da dieser Ansatz in bestimmten Fällen aus einem bestimmten Blickwinkel zu falschen Ergebnissen führt. Diese Modifikation der Technik wird als Parallaxen-Mapping mit Offset-Begrenzung bezeichnet . Die Wahl einer Ansatzoption bleibt größtenteils eine Frage der persönlichen Präferenz - zum Beispiel bin ich den Ergebnissen des üblichen Parallax Mapping-Algorithmus loyaler.

Die resultierenden veränderten Texturkoordinaten werden letztendlich verwendet, um aus der diffusen Karte und der normalen Karte auszuwählen, was einen ziemlich guten Oberflächenverzerrungseffekt ergibt (der Parameter height_scale wird hier nahe 0,1 gewählt):


Im Bild können Sie die Auswirkungen der Techniken Normal Mapping und Parallax Mapping vergleichen. Da Parallax Mapping Oberflächenunregelmäßigkeiten simuliert, sind bei dieser Technik Situationen möglich, in denen sich die Steine ​​je nach Blickrichtung überlappen.

Entlang der Ränder der strukturierten Ebene sind auch seltsame Artefakte sichtbar. Sie treten aufgrund der Tatsache auf, dass die durch den Parallax Mapping-Algorithmus verschobenen Texturkoordinaten außerhalb des Einheitsintervalls liegen und je nach Umhüllungsmodus unerwünschte Ergebnisse verursachen können. Eine einfache Möglichkeit, solche Artefakte zu entfernen, besteht darin, einfach alle Fragmente zu verwerfen, für die die Texturkoordinaten außerhalb des Einheitsintervalls liegen:

 texCoords = ParallaxMapping(fs_in.TexCoords, viewDir); if(texCoords.x > 1.0 || texCoords.y > 1.0 || texCoords.x < 0.0 || texCoords.y < 0.0) discard; 

Infolgedessen werden alle Fragmente mit verschobenen Texturkoordinaten, die aus dem Intervall [0, 1] herausfallen, verworfen und das Ergebnis der Parallaxen-Mapping-Aktion wird visuell akzeptabel. Offensichtlich ist diese Zurückweisungsmethode nicht universell und kann möglicherweise nicht auf einige Oberflächen oder Texturierungsfälle angewendet werden. Am Beispiel eines Flugzeugs funktioniert es jedoch perfekt und trägt dazu bei, den Effekt der Änderung des Reliefs des Flugzeugs zu verstärken:


Beispielquellen finden Sie hier .

Es sieht gut aus und die Leistung der Methode ist ausgezeichnet - alles, was es brauchte, war eine zusätzliche Probe aus der Textur! Die Einfachheit der Methode hat jedoch erhebliche Nachteile: Der Reliefeffekt kann leicht zerstört werden, wenn die Ebene in einem Winkel betrachtet wird (was auch für die normale Abbildung gilt) oder wenn Abschnitte in der Höhenkarte mit starken Wertänderungen vorhanden sind:


Der Grund für die Zerstörung der Illusion liegt in der Tatsache, dass der Algorithmus eine sehr grobe Annäherung an die reale Verschiebungsabbildung ist. Es können uns jedoch mehrere zusätzliche Tricks helfen, mit denen wir selbst bei Betrachtung eines Winkels oder bei Verwendung von Höhenkarten mit starken Änderungen nahezu perfekte Ergebnisse erzielen können. Zum Beispiel können wir mehrere Beispiele aus einer Höhenkarte verwenden, um den Punkt zu finden, der dem Punkt am nächsten liegt $$$\ color {blue} B$ .

Steiles Parallaxen-Mapping

Die Steep Parallax Mapping-Technik ist eine logische Weiterentwicklung des klassischen Parallax Mapping: Der gleiche Ansatz wird im Algorithmus verwendet, aber anstelle einer einzelnen Auswahl werden mehrere verwendet - zur besseren Annäherung des Vektors $$$\ color {brown} {\ bar {P}}$ wird verwendet, um den Punkt zu berechnen $$$\ color {blue} B$ . Aufgrund dieser zusätzlichen Abtastwerte ist das Ergebnis des Algorithmus visuell viel plausibler, selbst wenn scharfe Winkel zur Oberfläche betrachtet werden.

Die Grundlage des Steep PM-Ansatzes besteht darin, einen bestimmten Tiefenbereich in gleich große Schichten zu unterteilen. Als nächstes durchlaufen wir die Ebenen und verschieben gleichzeitig die ursprünglichen Texturkoordinaten in Richtung des Vektors $$$\ color {brown} {\ bar {P}}$ und Erstellen von Proben aus der Tiefenkarte, wobei in dem Moment angehalten wird, in dem die Tiefe der Probe geringer ist als die Tiefe der aktuellen Ebene. Schauen Sie sich das Diagramm an:


Wie Sie sehen können, bewegen wir uns von oben nach unten durch die Ebenen und vergleichen für jede Ebene ihre Tiefe mit dem Wert aus der Tiefenkarte. Wenn die Ebenentiefe kleiner als der Wert aus der Tiefenkarte ist, bedeutet dies, dass der Vektor $$$\ color {brown} {\ bar {P}}$ entsprechend dieser Schicht liegt über der Oberfläche. Dieser Vorgang wird wiederholt, bis die Ebenentiefe größer ist als die Auswahl aus der Tiefenkarte: in diesem Moment der Vektor $$$\ color {brown} {\ bar {P}}$ zeigt auf einen Punkt unterhalb der simulierten Oberflächentopographie.
Das Beispiel zeigt, dass die Auswahl aus der Tiefenkarte auf der zweiten Ebene ( $$$D (2) = 0,73$ ) liegt immer noch "tiefer" in Bezug auf die Tiefe der zweiten Schicht gleich 0,4, was bedeutet, dass der Suchprozess fortgesetzt wird. Im nächsten Durchgang stellt sich heraus, dass eine Ebenentiefe von 0,6 „über“ dem Wert der Probe aus der Tiefenkarte liegt ( $$$D (3) = 0,37$ ) Von hier schließen wir, dass der Vektor $$$\ color {brown} {\ bar {P}}$ Für die dritte Schicht wird die zuverlässigste Position für die verzerrte Oberflächengeometrie erhalten. Sie können Texturkoordinaten verwenden $$$T_3$ abgeleitet vom Vektor $$$\ color {brown} {\ bar {P}}$ , um die Texturkoordinaten des aktuellen Fragments zu versetzen. Offensichtlich wächst die Genauigkeit des Verfahrens mit der Anzahl der Schichten.

Änderungen in der Implementierung wirken sich nur auf die ParallaxMapping-Funktion aus, da sie bereits alle Variablen enthält, die für die Funktionsweise des Algorithmus erforderlich sind:

 vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir) { //    const float numLayers = 10; //    float layerDepth = 1.0 / numLayers; //    float currentLayerDepth = 0.0; //         //     P vec2 P = viewDir.xy * height_scale; vec2 deltaTexCoords = P / numLayers; [...] } 

Zuerst initialisieren wir: Legen Sie die Anzahl der Ebenen fest, berechnen Sie die Tiefe jeder Ebene und ermitteln Sie schließlich die Größe der Verschiebung der Texturkoordinaten entlang der Richtung des Vektors $$$\ color {brown} {\ bar {P}}$ , die auf jeder Ebene verschoben werden müssen.

Als nächstes folgt eine Passage durch die Ebenen, beginnend von oben, bis eine Auswahl aus der Tiefenkarte gefunden wird, die „über“ dem Tiefenwert der aktuellen Ebene liegt:

 //   vec2 currentTexCoords = texCoords; float currentDepthMapValue = texture(depthMap, currentTexCoords).r; while(currentLayerDepth < currentDepthMapValue) { //      P currentTexCoords -= deltaTexCoords; //          currentDepthMapValue = texture(depthMap, currentTexCoords).r; //     currentLayerDepth += layerDepth; } return currentTexCoords; 

In diesem Code durchlaufen wir alle Tiefenebenen und verschieben die ursprünglichen Texturkoordinaten, bis die Auswahl aus der Tiefenkarte geringer ist als die Tiefe der aktuellen Ebene. Der Versatz wird ausgeführt, indem von den ursprünglichen Texturkoordinaten des Deltas basierend auf dem Vektor subtrahiert wird $$$\ color {brown} {\ bar {P}}$ . Das Ergebnis des Algorithmus ist ein Versatzvektor von Texturkoordinaten, der mit viel größerer Genauigkeit als die klassische Parallaxenabbildung definiert wird.

Mit etwa 10 Mustern wird das Mauerwerksbeispiel viel realistischer, selbst wenn es aus einem Winkel betrachtet wird. Das Beste ist jedoch, dass die Vorteile von Steep PM auf Oberflächen mit einer Tiefenkarte sichtbar sind, deren Werte sich stark ändern. Zum Beispiel, wie bei diesem Holzspielzeug, das bereits früher demonstriert wurde:


Sie können den Algorithmus ein wenig weiter verbessern, wenn Sie die Funktionen der Parallax Mapping-Technik ein wenig analysieren. Wenn Sie die Oberfläche ungefähr normal betrachten, müssen Sie die Texturkoordinaten nicht stark verschieben, während bei einem Blickwinkel die Verschiebung zum Maximum tendiert (stellen Sie sich in beiden Fällen mental die Blickrichtung vor). Wenn Sie die Anzahl der Proben in Abhängigkeit von der Blickrichtung parametrisieren, können Sie eine Menge sparen, wenn keine zusätzlichen Proben benötigt werden:

 const float minLayers = 8.0; const float maxLayers = 32.0; float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir))); 

Das Ergebnis des Skalarprodukts der VektoransichtDir und der positiven Halbachse Z wird verwendet, um die Anzahl der Schichten im Intervall [ minSamples , maxSamples ] zu bestimmen, d. H. Die Blickrichtung bestimmt die erforderliche Anzahl von Iterationen des Effekts (im Tangentenraum ist die positive Halbachse Z senkrecht zur Oberfläche gerichtet). Wenn wir parallel zur Oberfläche schauen würden, würde der Effekt alle 32 Ebenen verwenden.

Geänderter Quellcode ist hier . Ich schlage auch vor, die Textur eines Holzspielzeugs herunterzuladen: diffuse , normale Karte, Tiefenkarte .

Nicht ohne Ansatz und Nachteile. Da die Anzahl der Samples alle gleich endlich ist, ist das Auftreten von Aliasing-Effekten unvermeidlich, wodurch die Übergänge zwischen den Schichten auffällig werden:


Sie können den Schweregrad des Artefakts verringern, indem Sie die Anzahl der verwendeten Samples erhöhen, aber es verbraucht ziemlich schnell die gesamte verfügbare Videoprozessorleistung. Es gibt mehrere Ergänzungen zu der Methode, die als Ergebnis nicht den ersten Punkt zurückgeben, der unter dem imaginären Relief der Oberfläche erschien, sondern den interpolierten Wert der beiden nächstgelegenen Schichten, wodurch wir die Position des Punktes weiter klären können $$$\ color {blue} B$ .

Von diesen Methoden werden am häufigsten zwei verwendet: Relief Parallax Mapping und Parallax Occlusion Mapping , wobei Relief PM die zuverlässigsten Ergebnisse liefert, aber auch etwas leistungsintensiver ist als Parallax Occlusion Mapping. Da Parallax Occlusion Mapping in der Qualität von Relief PM immer noch sehr ähnlich ist und gleichzeitig schneller arbeitet, bevorzugen sie es, es am häufigsten zu verwenden. Als nächstes wird die Implementierung von Parallax Occlusion Mapping betrachtet.

Parallax Occlusion Mapping

Die Parallax Occlusion Mapping-Methode arbeitet alle nach den gleichen Grundprinzipien wie Steep PM. Statt jedoch die Texturkoordinaten der ersten Ebene zu verwenden, bei der ein Schnittpunkt mit einem imaginären Relief gefunden wurde, verwendet die Methode eine lineare Interpolation zwischen zwei Ebenen: der Ebene nach und vor dem Schnittpunkt. Der Gewichtungskoeffizient für die lineare Interpolation basiert auf dem Verhältnis der aktuellen Relieftiefe zu den Tiefen beider betrachteten Schichten. Schauen Sie sich das Diagramm an, um besser zu verstehen, wie alles funktioniert:


Wie Sie sehen können, ist alles dem steilen PM sehr ähnlich. Es wird nur ein zusätzlicher Schritt zum Interpolieren der Texturkoordinaten der beiden Tiefenschichten neben dem Schnittpunkt hinzugefügt. Natürlich ist eine solche Methode nur eine Annäherung, aber viel genauer als eine steile PM.

Der Parallax Occlusion Mapping-Code ist zusätzlich zum Steep PM-Code und nicht zu kompliziert:

 [...] // ,    Steep PM //       , // ..  " " vec2 prevTexCoords = currentTexCoords + deltaTexCoords; //         //      float afterDepth = currentDepthMapValue - currentLayerDepth; float beforeDepth = texture(depthMap, prevTexCoords).r - currentLayerDepth + layerDepth; //    float weight = afterDepth / (afterDepth - beforeDepth); vec2 finalTexCoords = prevTexCoords * weight + currentTexCoords * (1.0 - weight); return finalTexCoords; 

In dem Moment, in dem die nach dem Schnittpunkt liegende Schicht mit dem imaginären Relief gefunden wird, bestimmen wir auch die Texturkoordinaten der vor dem Schnittpunkt liegenden Schicht. Als nächstes finden wir die Verschiebungen der imaginären Relieftiefe relativ zu den Tiefen der beiden betrachteten Schichten und verwenden ihr Verhältnis als Gewichtskoeffizienten für die weitere lineare Interpolation der Texturkoordinaten, die den beiden betrachteten Schichten entsprechen. Das Ergebnis der Interpolation wird von der Funktion zur zukünftigen Verwendung zurückgegeben.

Parallax Occlusion Mapping liefert überraschend visuell zuverlässige Ergebnisse, wenn auch mit kleinen Fehlern und Aliasing-Artefakten. Für einen Kompromiss in Geschwindigkeit und Qualität sind sie jedoch unbedeutend und erscheinen nur bei genauer Beobachtung der Oberfläche in der Nähe der Kamera oder bei sehr scharfen Betrachtungswinkeln.


Ein Beispielcode ist hier .

Parallax Mapping ist wirklich eine hervorragende Technik, mit der Sie die visuellen Details Ihrer Szene dramatisch verbessern können, hat aber natürlich auch Nachteile in Form von Artefakten, die bei der Implementierung der Technik im Projekt berücksichtigt werden sollten. Die Parallaxenzuordnung wird größtenteils auf ebenen Flächen wie Wänden oder Böden verwendet - wo es nicht so einfach ist, den Umriss des gesamten Objekts zu bestimmen, und der Blickwinkel der Oberfläche oft nahe an der Senkrechten liegt. In diesem Fall sind Parallax Mapping-Fehler vor dem Hintergrund erhöhter Oberflächendetails nahezu unsichtbar.

Boni vom Übersetzer:

Relief Parallax Mapping

Da der Autor der Vollständigkeit halber zwei Methoden zur Klärung des Ergebnisses von Steep PM erwähnt hat, werde ich den zweiten der Ansätze beschreiben.

Wie bei der Parallax Occlusion Mapping wird hier das Ergebnis der steilen PM-Ausführung verwendet, d. H. Wir kennen die Tiefen zweier Schichten, zwischen denen der eigentliche Schnittpunkt des Vektors liegt $$$\ color {orange} {\ bar {V}}$ mit Relief sowie die entsprechenden Texturkoordinaten $$$T_2$ und $$$T_3$ . Die Verfeinerung der Schätzung des Schnittpunkts bei dieser Methode beruht auf der Verwendung der binären Suche.

Schritte des Verfeinerungsalgorithmus:

• Führen Sie eine steile PM-Berechnung durch und erhalten Sie Texturkoordinaten $$$T_2$ und $$$T_3$ - In diesem Intervall liegt der Schnittpunkt des Vektors $$$\ color {green} {\ bar {V}}$ mit Oberflächentopographie. Die wahre Kreuzung ist mit einem roten Kreuz markiert.
• Teilen Sie den Versatz der Texturkoordinaten und die Höhe der Tiefenebene in zwei aktuelle Werte.
• Verschieben Sie die Texturkoordinaten vom Punkt $$$T_3$ in der dem Vektor entgegengesetzten Richtung $$$\ color {green} {\ bar {V}}$ um den Betrag der Verschiebung. Reduzieren Sie die Ebenentiefe um den aktuellen Wert für die Ebenengröße.
• Direkt binäre Suche. Die angegebene Anzahl von Iterationen wird wiederholt:
• 1. Wählen Sie aus der Tiefenkarte. Teilen Sie den aktuellen Texturversatz und die Tiefenebenengröße in zwei aktuelle Werte.
  2. Wenn die Stichprobengröße größer als die aktuelle Ebenentiefe ist, erhöhen Sie die Ebenentiefe um die aktuelle Ebenengröße und ändern Sie die Texturkoordinaten entlang des Vektors $$$\ color {green} {\ bar {V}}$ auf den aktuellen Offset.
  3. Wenn die Stichprobengröße kleiner als die aktuelle Ebenentiefe ist, reduzieren Sie die Ebenentiefe um die aktuelle Ebenengröße und ändern Sie die Texturkoordinaten entlang des inversen Vektors $$$\ color {green} {\ bar {V}}$ auf den aktuellen Offset.
  
  
• Die zuletzt erhaltenen Texturkoordinaten sind die Ergebnisse von Relief PM.

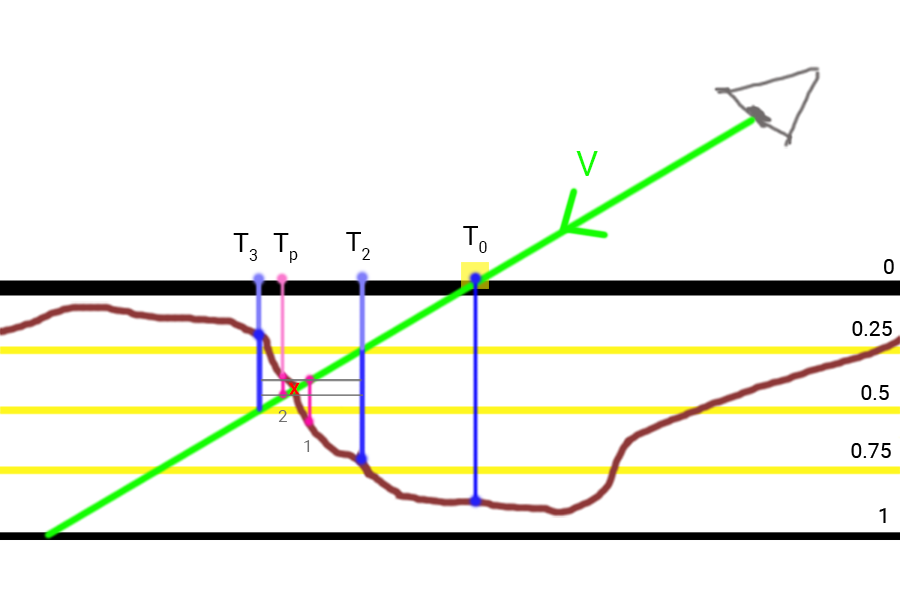
Das Bild zeigt das nach dem Finden der Punkte $$$T_2$ und $$$T_3$ Wir halbieren die Größe der Ebene und die Größe des Versatzes der Texturkoordinaten, wodurch wir den ersten Iterationspunkt der binären Suche erhalten (1). Da sich herausstellte, dass die Stichprobengröße größer als die aktuelle Tiefe der Ebene ist, halbieren wir die Parameter erneut und bewegen uns weiter $$$\ color {green} {\ bar {V}}$ Punkt (2) mit Texturkoordinaten erhalten $$$T_p$ Dies ist das Ergebnis von Steep PM für zwei Iterationen der binären Suche.

Shader Code:

 //  : inTexCoords -   , // inViewDir -      - //  : lastDepthValue –      //      vec2 reliefPM(vec2 inTexCoords, vec3 inViewDir, out float lastDepthValue) { // ====== // ,   Steep PM // ====== const float _minLayers = 2.; const float _maxLayers = 32.; float _numLayers = mix(_maxLayers, _minLayers, abs(dot(vec3(0., 0., 1.), inViewDir))); float deltaDepth = 1./_numLayers; // uDepthScale –     PM vec2 deltaTexcoord = uDepthScale * inViewDir.xy/(inViewDir.z * _numLayers); vec2 currentTexCoords = inTexCoords; float currentLayerDepth = 0.; float currentDepthValue = depthValue(currentTexCoords); while (currentDepthValue > currentLayerDepth) { currentLayerDepth += deltaDepth; currentTexCoords -= deltaTexcoord; currentDepthValue = depthValue(currentTexCoords); } // ====== //   Relief PM // ====== //         deltaTexcoord *= 0.5; deltaDepth *= 0.5; //      ,   Steep PM currentTexCoords += deltaTexcoord; currentLayerDepth -= deltaDepth; //    … const int _reliefSteps = 5; int currentStep = _reliefSteps; while (currentStep > 0) { currentDepthValue = depthValue(currentTexCoords); deltaTexcoord *= 0.5; deltaDepth *= 0.5; //       , //       if (currentDepthValue > currentLayerDepth) { currentTexCoords -= deltaTexcoord; currentLayerDepth += deltaDepth; } //       else { currentTexCoords += deltaTexcoord; currentLayerDepth -= deltaDepth; } currentStep--; } lastDepthValue = currentDepthValue; return currentTexCoords; } 

Selbstbeschattung

Auch eine kleine Ergänzung zum Hinzufügen von Schattierungen von einer ausgewählten Lichtquelle zum Berechnungsalgorithmus. Ich habe mich für das Hinzufügen entschieden, da die Berechnungsmethode technisch mit den oben genannten identisch ist, der Effekt jedoch immer noch interessant ist und Details hinzufügt.

Tatsächlich wird dieselbe steile PM angewendet, aber die Suche geht nicht tief in die simulierte Oberfläche entlang der Sichtlinie, sondern von der Oberfläche entlang des Vektors zur Lichtquelle$$$\color{green}{\bar{L}}$ .Dieser Vektor wird auch in den Tangentenraum übertragen und zur Bestimmung des Verschiebungsbetrags der Texturkoordinaten verwendet. Am Ausgang des Verfahrens wird im Intervall [0, 1] ein Materialbeleuchtungskoeffizient erhalten, mit dem die diffusen und Spiegelkomponenten in Beleuchtungsberechnungen moduliert werden.
Um eine Schattierung mit scharfen Kanten zu definieren, gehen Sie einfach entlang des Vektors$$ˉ L bis ein Punkt unter der Oberfläche liegt. Sobald ein solcher Punkt gefunden wird, nehmen wir den Beleuchtungskoeffizienten 0. Wenn wir die Tiefe Null erreichen, ohne einen unter der Oberfläche liegenden Punkt zu treffen, nehmen wir den Beleuchtungskoeffizienten gleich 1.Um die Schattierung mit weichen Kanten zu bestimmen, müssen mehrere auf dem Vektor liegende Punkte überprüft werden$\color{green}{\bar{L}}$

$$ˉ L und befindet sich unter der Oberfläche. Der Schattierungsfaktor wird gleich der Differenz zwischen der Tiefe der aktuellen Ebene und der Tiefe aus der Tiefenkarte genommen. Berücksichtigt wird auch die Entfernung des nächsten Punktes aus dem fraglichen Fragment in Form eines Gewichtskoeffizienten von (1,0 - stepIndex / numberOfSteps). Bei jedem Schritt wird ein Teilbeleuchtungskoeffizient bestimmt als:$\color{green}{\bar{L}}$

$$

$$PSF_i=(layerHeight_i - heightFromtexture_i)*(1.0-\frac{i}{numSteps})$$

Das Endergebnis ist der maximale Lichtfaktor aller partiellen:

$$

$$SF=max(PSF_i)$$

Das Schema der Methode:

Der Fortschritt der Methode für drei Iterationen in diesem Beispiel:

• Wir initialisieren den Gesamtlichtfaktor auf Null.
• Machen Sie einen Schritt entlang des Vektors $$ˉ L , auf den Punkt kommen$\color{green}{\bar{L}}$$$$H_a$ . Die Punkttiefe ist deutlich geringer als die Auswahl aus der Karte. $$H ( T L 1 ) - es befindet sich unter der Oberfläche. Hier haben wir die erste Prüfung durchgeführt und unter Berücksichtigung der Gesamtzahl der Prüfungen den ersten Teillichtfaktor gefunden und gespeichert: (1,0 - 1,0 / 3,0).$H(T_{L1})$
• Machen Sie einen Schritt entlang des Vektors $$ˉ L , auf den Punkt kommen$\color{green}{\bar{L}}$$$$H_b$ . Die Punkttiefe ist deutlich geringer als die Auswahl aus der Karte. $$H ( T L 2 ) - es befindet sich unter der Oberfläche. Die zweite Prüfung und der zweite Teilkoeffizient: (1,0 - 2,0 / 3,0).$H(T_{L2})$
• Wir machen noch einen Schritt entlang des Vektors und erreichen die minimale Tiefe von 0. Stoppen Sie die Bewegung.
• Definition des Ergebnisses: Wenn keine Punkte unter der Oberfläche gefunden wurden, geben wir einen Koeffizienten von 1 zurück (keine Schattierung). Andernfalls wird der resultierende Koeffizient zum Maximum der berechneten Teilkoeffizienten. Für die Verwendung in Beleuchtungsberechnungen subtrahieren wir diesen Wert von der Einheit.

Shader-Code-Beispiel:

 //  : inTexCoords -   , // inLightDir -       - //  : inLastDepth –    , //      PM //       //    float getParallaxSelfShadow(vec2 inTexCoords, vec3 inLightDir, float inLastDepth) { float shadowMultiplier = 0.; //      , //    float alignFactor = dot(vec3(0., 0., 1.), inLightDir); if (alignFactor > 0.) { //   :  ,  //  ,     const float _minLayers = 16.; const float _maxLayers = 32.; float _numLayers = mix(_maxLayers, _minLayers, abs(alignFactor)); float _dDepth = inLastDepth/_numLayers; vec2 _dtex = uDepthScale * inLightDir.xy/(inLightDir.z * _numLayers); //  ,    int numSamplesUnderSurface = 0; //       //     L float currentLayerDepth = inLastDepth - _dDepth; vec2 currentTexCoords = inTexCoords + _dtex; float currentDepthValue = depthValue(currentTexCoords); //    float stepIndex = 1.; // ,       … while (currentLayerDepth > 0.) { //     ,     //       if (currentDepthValue < currentLayerDepth) { numSamplesUnderSurface++; float currentShadowMultiplier = (currentLayerDepth - currentDepthValue)*(1. - stepIndex/_numLayers); shadowMultiplier = max(shadowMultiplier, currentShadowMultiplier); } stepIndex++; currentLayerDepth -= _dDepth; currentTexCoords += _dtex; currentDepthValue = depthValue(currentTexCoords); } //      ,   //      1 if (numSamplesUnderSurface < 1) shadowMultiplier = 1.; else shadowMultiplier = 1. - shadowMultiplier; } return shadowMultiplier; } 

Der resultierende Koeffizient wird verwendet, um das Ergebnis des in den Beispielen verwendeten Blinn-Fong-Beleuchtungsmodells zu modulieren:

 [...] //      vec3 fullColorADS = ambientTerm + attenuation * (diffuseTerm + specularTerm); //     -  fullColorADS *= pmShadowMultiplier; return fullColorADS; 

Vergleich aller Methoden in einer Collage, 3 MB Volumen.

Auch ein Videovergleich:

Zusätzliche Materialien

• Parallax Occlusion Mapping in GLSL : Eine großartige Parallax Mapping-Lektion von sunandblackcat.com .
• Funktionsweise der Parallaxenverschiebungszuordnung : Ein Video-Tutorial, in dem die Details der Parallaxenzuordnung von TheBennyBox erläutert werden .

PS : Wir haben ein Telegramm Conf für die Koordination der Überweisungen. Wenn Sie ernsthaft bei der Übersetzung helfen möchten, sind Sie herzlich willkommen!