Tupper-Formel und Implementierung des Algorithmus in Python

Anstelle des Vorworts

Vor nicht allzu langer Zeit habe ich im Internet von einer so wunderbaren und erstaunlichen Kopie der babylonischen Bibliothek wie der Tapper-Formel erfahren. Es ist eher Tuppers Ungleichung als die Formel. Die Besonderheit dieser Ungleichung besteht darin, dass sie ein eigenes Bild auf dem Diagramm erzeugt. Schau dir dieses Wunder an!



(Wikipedia-Quelle)

Was Sie auf dem Bild sehen, ist die Formel desselben Jeff Tupper. Wahrscheinlich ist die Hälfte der Leser bereits zu Wolfram gegangen, um das Ergebnis dieser Ungleichung zu ziehen ... Aber das ist nicht so einfach. Wie Sie in diesem Bild sehen können, ist die Formel in der Grafik auf einem Segment entlang der Achse OY [k; k + 15]. Was ist diese mysteriöse Zahl k? Wo kann man es bekommen? Die Sache ist, dass diese Ungleichung nach dem Konzept der babylonischen Bibliothek absolut jedes Bild mit einer Auflösung von 106x17 anzeigen kann! Jedes Bild hat seine eigene Position im Diagramm und damit eine eindeutige Zahl k. Somit gibt es für jede Zahl k ein einzelnes Bild auf dem gesamten Graphen !

Für ein gegebenes Bild ist die Zahl k wie folgt:

4858450636189713423582095962494202044581400587983244549483093085061934704708809928450644769865524364849997247024915119110411605739177407856919754326571855442057210445735883681829823754139634338225199452191651284348332905131193199953502413758765239264874613394906870130562295813219481113685339535565290850023875092856892694555974281546386510730049106723058933586052544096664351265349363643957125565695936815184334857605266940161251266951421550539554519153785457525756590740540157929001765967965480064427829131488548259914721248506352686630476300

Es ist interessant, Leute zu betrachten, die zu einer solchen Koordinate scrollen, um die Formel zu sehen

Mir kam der Gedanke, ein Programm in Python3 zu schreiben, das ein Bild in eine Zahl k und umgekehrt konvertiert und Ihnen eine andere großartige Möglichkeit zum Codieren eines Bildes in eine Zahl beschreibt.

Theorie

(Hinzugefügt) Wie funktioniert es?

Werfen wir einen Blick auf die Formel selbst:

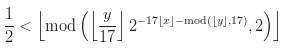
Definieren wir die Syntax:
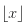
- Nummer abgerundet
mod (x, y) - Rest der Division von x durch y

Und dann scheint alles klar zu sein.
Beachten Sie, dass sowohl x als auch y abgerundet sind. Es ist diese Rundung, die uns letztendlich ein Pixelbild gibt


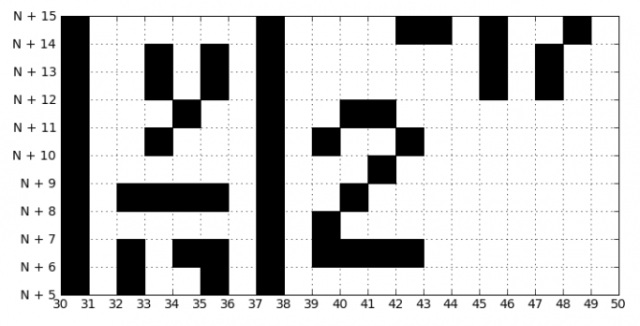
Bezeichnen Sie alles, was auf der rechten Seite der Ungleichung gerundet ist, mit $$$\ alpha$.
Dann

$$

$$1/2 <[\ alpha] <=> 1 <= [\ alpha]$$

Was offensichtlich ist, weil der gesamte Ausdruck abgerundet ist.

Sei y = 17r + q, wobei r der ganzzahlige Teil der Division von y durch 17 ist und r der Rest der Division ist. Somit können wir in der Formel ersetzen $$$[j / 17]$auf r und $$$mod (y, 17)$auf q.

Wir bekommen

$$

$$1 <= mod (q * 2 ^ {- 17-r}, 2)$$

Oder sonst

$$

$$1 <= mod (q / 2 ^ {17x + r}, 2)$$

mod ( $$$\ alpha$, 2) nimmt 2 Werte an - 0 oder 1. Dementsprechend sagt diese Ungleichung aus, ob die Zahl $$$q / 2 ^ {17x + r}$sogar oder nicht.

Beachten Sie, dass das Bild im Intervall [N, N + 16] angezeigt wird $$$q = [y / 17]$bleibt über die gesamte Bildhöhe konstant, was nicht über die Zahl r gesagt werden kann (über das gesamte Bild variiert sie von 0 bis 16).

Und jetzt die Kirsche auf dem Kuchen. Nummer $$$[q / {2 ^ {17x + r}}]$wird genau dann ungerade sein, wenn die Bitzahl (17x + r) in der Binärdarstellung von q gleich 1 ist. Und da sich die Zahl q mit ihrer Höhe und auch ihrer Binärdarstellung ständig ändert, erhalten wir jedes Mal ein eindeutiges Bild! Genau das funktioniert Tappers Formel.

Nun wollen wir sehen, wie man die Höhe berechnet, in der wir unser Bild sehen wollen

Das Prinzip der Berechnung der Zahl k

Tupper selbst beschrieb die Berechnung der Zahl k für jedes 106x17-Bild (dies ist wichtig!) Wie folgt:

1. Bild in Schwarzweiß konvertieren
2. Lesen Sie jedes Pixel von unten nach oben, von links nach rechts und legen Sie es in den Puffer. Wenn das Pixel schwarz ist, setzen Sie 1, wenn weiß - 0.
3. Konvertieren Sie Binär in Dezimal und multiplizieren Sie mit 17
4. Gewinn!

Um ein Bild von der Zahl k zu erhalten, machen wir alles genau umgekehrt. Nun, lass uns codieren gehen!

Kodim

UPD: In den Kommentaren haben die Leute den Code ein wenig verbessert, ihn einfacher und transparenter gemacht. Dieser Artikel hat Aktualisierungsdaten veröffentlicht. Wenn Sie die alten Versionen des Codes sehen möchten, gehen Sie zum Github-Repository (bis Sie es festschreiben, Link am Ende des Artikels) und im Kommentar

Von k zum Bild

UPD

Auf Wunsch von Kommentatoren wurde eine neue Methode hinzugefügt, um das Bild unter Verwendung dieser Ungleichung und k! Jetzt werden wir keine Manipulationen mit der Zahl vornehmen, auf das Binärsystem übertragen, sondern die Funktion selbst direkt beeinflussen!

Verwenden der Tapper-Methode zum Decodieren der Zahl k

Wir bekommen die Zahl k vom Benutzer, mit geschlossenen Augen teilen wir sie durch 17 und übersetzen sie in das Binärsystem.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:] 

Wir verstehen, dass einige Anfangspixel weiß sein können (gleich 0), für unsere Binärzahl sind die ersten Bits Nullen, und wenn eine Zahl in ein Dezimalsystem übersetzt wird, gehen diese Anfangsnullen verloren. Daher überprüfen wir die Größe der resultierenden Binärzahl. Wenn sie kleiner als 1802 ist, fügen wir am Anfang Nullen hinzu.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:] #   RadicalDreamer binary = ("0" * (1802 - len(binary))) + binary 

Deklarieren Sie als Nächstes eine zweidimensionale Liste, in der Informationen zu jeder Bildzeile gespeichert werden. Dann schreiben wir alle Bits auf, die wir lesen (vergessen Sie nicht den Algorithmus, mit dem die Zahl k erstellt wird - von unten nach oben, von links nach rechts)

 lists = [[] for x in range(17)] #C   RadicalDreamer for x in range(1802): lists[-(x % 17)].append(binary[x]) <b> !</b> <source lang="python"> #-----!-----# image = Image.new("1", (106,17), (0)) # -  10617 draw = image.load() for y in range(17): for x in range(106): image.putpixel(xy=(105-x,16-y), value=(int(lists[y][x]),)) #    ,      lists image.save("image.png") #  

Lassen Sie uns versuchen, die Zahl k, die ich am Anfang des Artikels angegeben habe, in unser Programm aufzunehmen und Folgendes zu erhalten:



Wie Sie sehen, hat alles für uns geklappt, und jetzt können wir jedes k dekodieren!

Verwenden von Ungleichung, um ein Bild aus k zu erzeugen

Schreiben Sie zunächst die Funktion in Python:

 def f(x,y): return ((y//17)//(1 << (17*x+(y%17))))%2 

Dank der Operatoren // und << wurde die Implementierung der Funktion erheblich vereinfacht. Es ist garantiert, dass die Zahlen x und y ganze Zahlen sind !

Wir erstellen erneut eine zweidimensionale Liste, in der wir die Bits des Bildes speichern und mithilfe von Schleifen Informationen über jede Zeile darin schreiben

 lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2)) 

Und dann zeichnen wir wie im vorherigen Beispiel ein Bild mit der PIL-Bibliothek.

Die volle Funktion sieht so aus:

 def from_k_to_bin(k: int) -> list: lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2)) return lists 

Bild in k

Nun lernen wir, jedes Bild in die Zahl k zu kodieren.

Zuerst bekommen wir das Bild selbst

 def get_image() -> Image: name = input("   (      ):") try: im = Image.open(name) except Exception: print("!") exit(0) return im 

Überprüfen Sie die Größe

 _SIZE_WIDTH = 106 _SIZE_HEIGHT = 17 image = get_image() width, height = image.size flag_okay = False if width == _SIZE_WIDTH and height == _SIZE_HEIGHT: flag_okay = True if not flag_okay: print("  ") print(width, height) exit(0) print(" !") 

Wir machen das Bild schwarz und weiß und beginnen Pixel für Pixel zu lesen:

 image = image.convert('1') byteset = "" for x in range(105,-1,-1): for y in range(0,17): #c m03r   if image.getpixel((x,y)) > 127: byteset += '1' else: byteset += '0' 

Es bleibt nur die Konvertierung in das Dezimalsystem und die Multiplikation mit 17.

 k = int(byteset,2)*17 print(" :") print(k) 

Nun, lass uns testen gehen!

Ich habe beschlossen, das habr-Logo zu codieren. Hier ist das Quellbild:



Wir starten das Programm und geben den Bildnamen an:



Wir haben folgendes k:

4858487703217654168507377107565676789145697178497253677539145555247620343537955749299116772611982962556356527603203744742682135448820545638134012705381689785851604674225344958377377969928942310236199337805399065932982909660659786056259547094494380793146587709009524498386724160055692719747815828234655968636671461350354316223620304956111171025410498514602810746287134775641383930152393933036921599511277388743068766568352667661462097979110006690900253037600818522726237351439443865433159187625289316917268254866954663750093103703327097252478959

Lassen Sie es uns in unserem eigenen Programm ausprobieren.

Hier ist das Bild, das wir erhalten haben:



Es war ein wenig verzerrt aufgrund einer leicht krummen Übersetzung des Bildes in Schwarzweiß.

Zusammenfassung

Quellcode: Github

Quellen: Wiki-Artikel