In einem kürzlich erschienenen Artikel, "
Amplitudenmodulation eines beliebigen Signals ", versuchte der Autor ziemlich verwirrt, sein Verständnis der Bildung des Spektrums mit Amplitudenmodulation zu präsentieren. Das Fehlen von Illustrationen und ein Übermaß an Mathematik mit integralen Transformationen hinderten die Community jedoch daran, die Gedanken des Autors zu verstehen und den Artikel zu schätzen. Das Thema ist zwar recht einfach - und wir werden versuchen, es erneut zu betrachten, diesmal mit Bildern und Wolfram Mathematica.
Die Idee der Amplitudenmodulation besteht also darin, ein niederfrequentes Signal - Sprache oder Musik - zu übertragen, das ein hochfrequentes (Träger-) Signal moduliert, den hörbaren Bereich um ein Vielfaches überschreitet und ein schmales Frequenzband in der Luft einnimmt. Die Modulation selbst erfolgt durch einfaches Multiplizieren des Signals mit dem Träger:

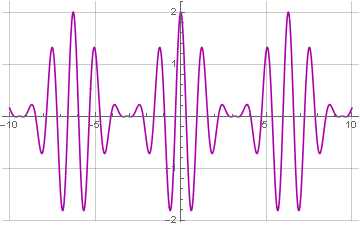
Hier haben wir eine Sinuswelle mit einer Frequenz von 5:


Und das Signal selbst - mit einer Frequenz von 1:

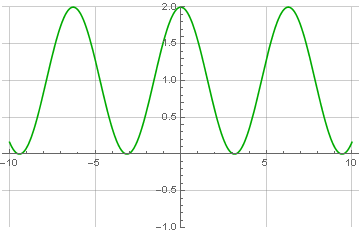
Möglicherweise stellen Sie fest, dass das Signal nach oben verschoben ist und nur positive Werte aufweist. Dies ist kein Zufall und eine Voraussetzung für die Möglichkeit einer späteren korrekten Wiederherstellung. Wie kann ich es wiederherstellen? Sehr einfach! Es ist notwendig, die Phase des modulierten Signals um 90 Grad zu verschieben (die als
Hilbert-Transformation bekannte Operation) und die Wurzel der Summe der Quadrate der modulierten und konvertierten Signale zu berechnen:

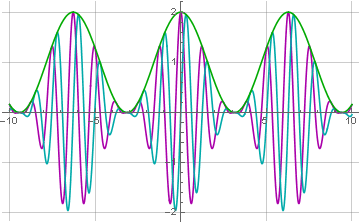
In einer einfacheren (aber groben) Version kann die Hilbert-Transformation durch eine Signalverzögerung um ein Viertel der Trägerfrequenzperiode ersetzt werden, und das endgültige Signal kann zusätzlich durch ein Tiefpassfilter gefiltert werden. In einer noch einfacheren Version können Sie die Wurzeln und Quadrate überhaupt nicht zählen, sondern das Signal nach dem Absolutwert filtern (der normalerweise in Funkempfängern verwendet wird).
Nun wollen wir sehen, was mit den Spektren passiert. Wir berechnen die Fourier-Transformation des Trägers:


Da die Dirac-Delta-Funktion keine Funktion im klassischen Sinne ist, kann ihr Graph nicht auf standardmäßige Weise konstruiert werden. Daher werden wir es manuell mit dem allgemein akzeptierten Stil tun:

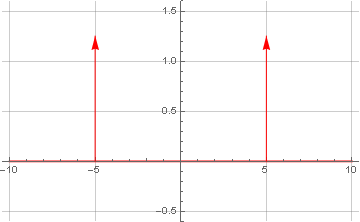
Erwartete erhalten die gleiche Frequenz wie in der Ausgangsformel. Das Vorhandensein einer weiteren Frequenz derselben Frequenz, jedoch mit einem Minuszeichen, ist kein Zufall - dieses Phänomen wird als
hermitische Symmetrie bezeichnet und ist eine Folge der Tatsache, dass die betreffende Funktion rein real ist und in der komplexen Darstellung eine imaginäre Komponente von Null aufweist. Das Fehlen imaginärer Komponenten im Spektrum nach der Transformation ist darauf zurückzuführen, dass unsere Funktionen anfangs gerade sind (symmetrisch zu Null).
Jetzt machen wir die Fourier-Transformation für das Signal selbst:



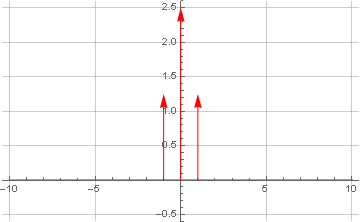
Hier haben wir zusätzlich die Dirac-Delta-Funktion im Koordinatenzentrum erhalten - aufgrund des Vorhandenseins einer konstanten Komponente im Signal, die per Definition keine Schwingungen aufweist -, die es uns ermöglicht, sie als Nullfrequenz zu betrachten.
Was passiert mit dem Spektrum, wenn sie multipliziert werden? Mal sehen:



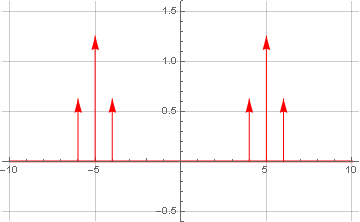
Aus der Theorie wissen wir, dass die Multiplikation im Zeitbereich der Faltung im Frequenzbereich entspricht (und umgekehrt, was bei der FIR-Filterung weit verbreitet ist). Und da eines der der Faltung unterworfenen Signale nur aus einer (positiven und negativen) Frequenz bestand, haben wir als Ergebnis der Faltung nur eine lineare Übertragung des Signals in der Frequenz nach oben (in beide Richtungen) erhalten. Und da die Symmetrie erhalten bleibt, hat das Signal immer noch keine imaginäre Komponente.
Wir bringen es nun in eine komplexe (
analytische ) Form und setzen den negativen Frequenzbereich auf Null:

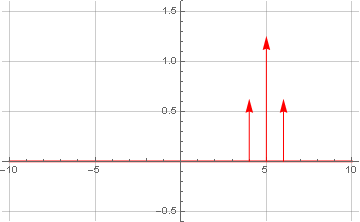
und mache die inverse Fourier-Transformation:


Da die Funktion jetzt komplex ist, müssen zum Erstellen ihres Graphen die realen und imaginären Komponenten getrennt extrahiert werden:

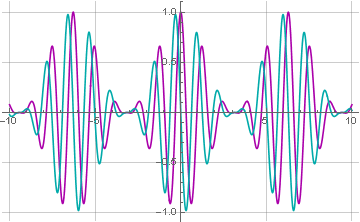
Jetzt hat unser Signal eine imaginäre Komponente, bei der es sich um das um 90 Grad verschobene Originalsignal handelt. Dies wird offensichtlicher, wenn wir die resultierende Funktion in trigonometrischer Form darstellen:

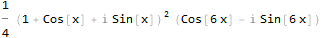
Noch nicht sehr offensichtlich. Versuchen wir zu vereinfachen:

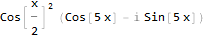
Jetzt sieht es eher nach Wahrheit aus - und wie Sie sehen, wurde auch die Funktion unseres ursprünglichen Signals vereinfacht. Versuchen wir, die ursprüngliche Form wiederherzustellen:
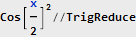

Der 1/2 Faktor ist nicht zufällig aufgetreten - nachdem wir die Hälfte des Spektrums auf Null gesetzt hatten, haben wir die Signalleistung entsprechend reduziert. Nun, da wir ein moduliertes komplexes Signal haben, können wir dieses Modul verwenden, um Folgendes zu berechnen:

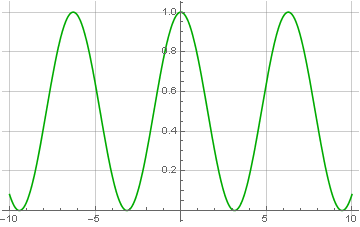
Der Modul einer komplexen Zahl wird genau durch die Wurzel der Summe der Quadrate der imaginären und realen Komponenten berechnet. Und daraus wird klar, warum das codierte Signal nur aus positiven Werten bestehen sollte - wenn es negative Werte enthält, werden sie nach der Wiederherstellung auch positiv, was als Übermodulation bezeichnet wird:

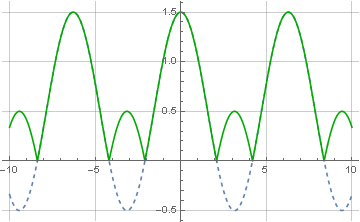
Die Signalwiederherstellung ist auch mit Hilfe eines Quadratur-Lokaloszillators möglich - wenn das modulierte Signal erneut mit der Trägerfrequenz multipliziert wird, diesmal jedoch komplex:





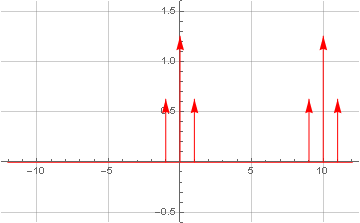
Aufgrund der Tatsache, dass die komplexe Frequenz im Frequenzbereich nur einen Impuls hat, ohne ihn im negativen Frequenzbereich zu duplizieren, erhalten wir als Ergebnis der Faltung einen linearen Spektrumtransfer, bei dem der negative Teil des Spektrums in die Mitte zurückkehrt und der positive Teil sich noch weiter bewegt, und Es wird nur von einem Tiefpassfilter gefiltert.
Fazit
Wie Sie sehen können, ist es nicht kompliziert, die Amplitudenmodulation durch die Fourier-Transformation zu betrachten. Wenn wir es ausschließlich auf Schulebene betrachten, genügt es, daran zu erinnern, dass das Produkt der (Träger-) Summe (die das Signal in Form einer trigonometrischen Reihe darstellt) der Summe der Produkte entspricht (jedes Mitglied der Reihe einzeln mit der Trägerfrequenz) - und dementsprechend wird jedes dieser Produkte in zerlegt die Summe zweier Sinuskurven nach der Formel, die der Autor des Originalartikels bereits geäußert hat.
Ein aufmerksamer Leser könnte auch feststellen, dass, da die Modulation zu einem in Bezug auf die Trägerfrequenz symmetrischen Spektrum führte, Datenredundanz besteht und Sie nur ein Seitenband belassen können, wodurch das belegte Frequenzband in der Luft reduziert wird. Eine solche Technologie gibt
es zwar , aber das ist eine ganz andere Geschichte.