Grüße an alle, insbesondere an diejenigen, die sich für diskrete Mathematik und Graphentheorie interessieren.
Hintergrund
Es ist einfach so passiert, dass ich aus Interesse einen Tour-Baudienst entwickelt habe. Routen. Die Aufgabe bestand darin, die besten Routen basierend auf der für den Benutzer interessanten Stadt, den Kategorien von Einrichtungen und dem Zeitrahmen zu planen. Nun, eine der Unteraufgaben bestand darin, die Reisezeit von einer Institution zur anderen zu berechnen. Da ich jung und dumm war, habe ich dieses Problem direkt mit dem Dijkstra-Algorithmus gelöst, aber fairerweise ist es erwähnenswert, dass nur damit die Iteration von einem Knoten zu Tausenden von anderen gestartet werden konnte. Das Zwischenspeichern dieser Entfernungen war keine Option, Einrichtungen mehr als 10k nur in Moskau allein und Entscheidungen wie die Entfernung von Manhattan in unseren Städten funktionieren überhaupt nicht.
Es stellte sich heraus, dass es möglich war, das Leistungsproblem im Kombinatorikproblem zu lösen, aber die meiste Zeit für die Verarbeitung der Anforderung wurde für die Suche nach nicht zwischengespeicherten Pfaden aufgewendet. Das Problem wurde durch die Tatsache erschwert, dass der Osm-Straßengraph in Moskau ziemlich groß ist (eine halbe Million Knoten und 1,1 Millionen Bögen).
Ich werde nicht über alle Versuche sprechen und dass das Problem tatsächlich durch Abschneiden der zusätzlichen Bögen des Diagramms gelöst werden könnte. Ich werde Ihnen nur sagen, dass es mir irgendwann dämmerte und ich erkannte, dass, wenn Sie sich dem Dijkstra-Algorithmus unter dem Gesichtspunkt des probabilistischen Ansatzes nähern, es kann linear sein.
Dijkstra für die logarithmische Zeit
Jeder weiß, aber wer weiß, dass der Dijkstra-Algorithmus unter Verwendung einer Warteschlange mit der logarithmischen Komplexität des Einfügens und Löschens zur Komplexität der Form O (n log (n) + m log (n)) führen kann. Bei Verwendung des Fibonacci-Heaps kann die Komplexität auf O (n * log (n) + m) reduziert werden, aber immer noch nicht linear, aber ich möchte.
Im allgemeinen Fall wird der Warteschlangenalgorithmus wie folgt beschrieben:
Lassen Sie:
- V ist die Menge der Graphenscheitelpunkte
- E ist die Menge der Kanten des Graphen
- w [i, j] ist das Gewicht der Kante von Knoten i zu Knoten j
- a - Scheitelpunkt der Suche starten
- q-Vertex-Warteschlange
- d [i] - Abstand zum i-ten Knoten
- d [a] = 0, für alle anderen d [i] = + inf
Während q nicht leer ist:
- v ist der Scheitelpunkt mit dem Minimum d [v] von q
- Für alle Eckpunkte u, für die es einen Übergang von Eckpunkt v zu E gibt
- wenn d [u]> w [vu] + d [v]
- entferne u von q mit dem Abstand d [u]
- d [u] = w [vu] + d [v]
- addiere u zu q mit dem Abstand d [u]
- entferne v von q
Wenn wir einen rot-schwarzen Baum als Warteschlange verwenden, in der das Einfügen und Löschen in log (n) erfolgt und die Suche nach dem minimalen Element in log (n) ähnlich ist, ist die Komplexität des Algorithmus O (n log (n) + m log (n)). .
Und hier ist ein wichtiges Merkmal zu erwähnen: Theoretisch hindert nichts daran, die Spitze mehrmals zu betrachten. Wenn der Scheitelpunkt untersucht und der Abstand zu ihm auf einen falschen Wert aktualisiert wurde, der größer als der wahre Wert ist, ist es zulässig, solche Tricks auszuführen, sofern das System früher oder später konvergiert und der Abstand zu u auf den richtigen Wert aktualisiert wird. Es ist jedoch erwähnenswert, dass ein Scheitelpunkt mit einer geringen Wahrscheinlichkeit mehr als einmal berücksichtigt werden sollte.
Hash-Tabelle sortieren
Um die Laufzeit des Dijkstra-Algorithmus auf eine lineare zu reduzieren, wird eine Datenstruktur vorgeschlagen, bei der es sich um eine Hash-Tabelle mit Knotennummern (node_id) als Werten handelt. Ich stelle fest, dass die Notwendigkeit für das d-Array nicht verschwindet, sondern immer noch benötigt wird, um die Entfernung zum i-ten Knoten in konstanter Zeit zu ermitteln.
Die folgende Abbildung zeigt ein Beispiel für die vorgeschlagene Struktur.
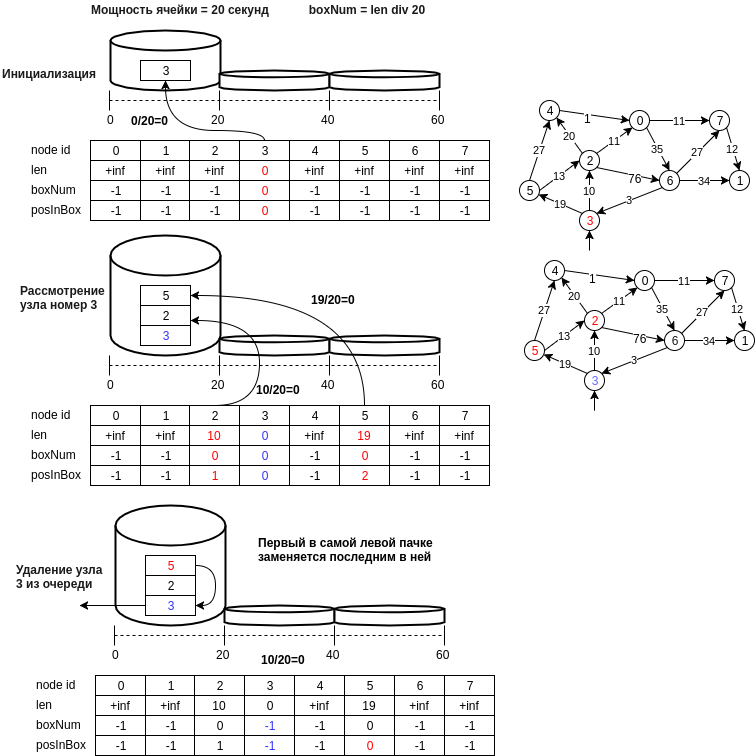
Beschreiben wir schrittweise die vorgeschlagene Datenstruktur:
- Der Knoten u wird mit einer Zahl gleich d [u] // Bucket_size in die Zelle geschrieben, wobei Bucket_size die Leistung der Zelle ist (z. B. 20 Meter, dh die Zelle mit der Nummer 0 enthält Knoten, deren Abstand im Bereich [0, 20) Meter liegt )
- der letzte Knoten der ersten nicht leeren Zelle, d.h. Der Vorgang des Extrahierens des minimalen Elements wird in O (1) ausgeführt. Es ist notwendig, den aktuellen Status der Kennung der Nummer der ersten nicht leeren Zelle (min_el) beizubehalten.
- Die Einfügeoperation wird ausgeführt, indem am Ende der Zelle eine neue Knotennummer hinzugefügt wird und auch O (1) ausgeführt wird, weil Die Berechnung der Zellenzahl erfolgt in konstanter Zeit.
- Bei der Löschoperation ist, wie im Fall einer Hash-Tabelle, eine normale Aufzählung möglich, und man könnte eine Annahme treffen und sagen, dass dies bei einer kleinen Zellengröße auch O (1) ist. Wenn Ihnen der Speicher nichts ausmacht (im Prinzip und nicht viel benötigt wird, ein anderes Array von n), können Sie ein Array von Positionen in der Zelle erstellen. In diesem Fall muss der letzte Wert in der Zelle an die gelöschte Stelle verschoben werden, wenn das Element in der Mitte der Zelle gelöscht wird.
- Ein wichtiger Punkt bei der Auswahl des minimalen Elements: Es ist nur mit einer gewissen Wahrscheinlichkeit minimal, aber der Algorithmus überprüft die Zelle min_el, bis sie leer ist, und früher oder später wird das tatsächliche minimale Element berücksichtigt, und wenn wir versehentlich den Wert der Entfernung zum Knoten aktualisiert haben, von dem aus erreichbar ist Minimum, dann können sich neben dem Minimum befindliche Knoten wieder in der Warteschlange befinden und der Abstand zu ihnen ist korrekt usw.
- Sie können auch leere Zellen bis min_el löschen und so Speicherplatz sparen. In diesem Fall muss das Entfernen des Knotens v aus der Warteschlange q erst erfolgen, nachdem alle benachbarten Knoten berücksichtigt wurden.
- Sie können auch die Zellenleistung, die Parameter zum Erhöhen der Zellengröße und die Anzahl der Zellen ändern, wenn Sie die Größe der Hash-Tabelle erhöhen müssen.
Messergebnisse
Die osm-Karte von Moskau wurde überprüft, über osm2po in Postgres entladen und dann in den Speicher geladen. Tests wurden in Java geschrieben. Es gab 3 Versionen des Diagramms:
- Quellgraph - 0,43 Millionen Knoten, 1,14 Millionen Bögen
- komprimierte Version des Diagramms mit 173.000 Knoten und 750.000 Bögen
- Fußgängerversion der komprimierten Version des Diagramms, 450.000 Bögen, 100.000 Knoten.
Unten sehen Sie ein Bild mit Messungen an verschiedenen Versionen des Diagramms:

Berücksichtigen Sie die Abhängigkeit der Wahrscheinlichkeit einer erneuten Anzeige des Scheitelpunkts und der Größe des Diagramms:
| Anzahl der Knotenansichten | Scheitelpunkte zählen | Wahrscheinlichkeit einer erneuten Anzeige des Knotens |
|---|
| 104915 | 100015 | 4.8 |
| 169429 | 167892 | 0,9 |
| 431490 | 419594 | 2.8 |
Möglicherweise stellen Sie fest, dass die Wahrscheinlichkeit nicht von der Größe des Diagramms abhängt und eher spezifisch für die Anforderung ist. Sie ist jedoch klein und ihr Bereich wird durch Ändern der Zellenleistung konfiguriert. Ich wäre sehr dankbar für die Hilfe bei der Erstellung einer probabilistischen Modifikation des Algorithmus mit Parametern, die ein Konfidenzintervall garantieren, in dessen Bereich die Wahrscheinlichkeit einer wiederholten Anzeige einen bestimmten Prozentsatz nicht überschreitet.
Es wurden auch qualitative Messungen durchgeführt, um den Vergleich der Richtigkeit des Ergebnisses der Algorithmen mit der neuen Datenstruktur praktisch zu bestätigen, die eine vollständige Übereinstimmung der kürzesten Pfadlänge von 1000 zufälligen Knoten zu 1000 anderen zufälligen Knoten in der Grafik zeigte. (und so weiter 250 Iterationen) beim Arbeiten mit einer Sortier-Hash-Tabelle und einem rot-schwarzen Baum.
Der Quellcode der vorgeschlagenen Datenstruktur befindet sich unter dem Link
PS: Ich kenne den Torup-Algorithmus und die Tatsache, dass er das gleiche Problem in linearer Zeit löst, aber ich konnte diese grundlegende Arbeit nicht an einem Abend beherrschen, obwohl ich die Idee allgemein verstanden habe. Zumindest, so wie ich es verstehe, wird dort ein anderer Ansatz vorgeschlagen, der auf der Erstellung eines minimalen Spannbaums basiert.
PSS Innerhalb einer Woche werde ich versuchen, die Zeit zu finden und einen Vergleich mit dem Fibonacci-Haufen anzustellen und etwas später eine Github-Rübe mit Beispielen und Testcodes hinzuzufügen.