Bei der Lösung von Problemen der Datenübertragung durch durch Frequenzkennlinien dargestellte Leitungen werden Fourier-Transformationen angewendet - die Übertragung von Signalen vom Zeitbereich in den Frequenzbereich und umgekehrt. Die MATLAB-Umgebung verfügt über alle Funktionen zur Lösung solcher Probleme. In dieser Arbeit wird ein Beispiel für die Berechnung der Reaktion eines über eine Leitung übertragenen Signals in MATLAB analysiert, dessen Charakteristik bei Frequenzen gemessen wird, die nicht mit der Datenübertragungsfrequenz übereinstimmen. Ich hoffe, dass dieses Beispiel das Verständnis der Funktionen der Signalumwandlungstechnologie in der MATLAB-Umgebung erleichtert.
Aufgabenbedingung
Es ist notwendig, die Änderung der Form des binären digitalen Signals zu bestimmen, das durch das Filter und die Signalleitung läuft. Das Signal wird durch die Amplitude und die Übertragungsrate eingestellt. Das auf die Datenübertragungsfrequenz normierte Filter zweiter Ordnung wird durch Zeitkonstanten eingestellt. Die Übertragungsfunktion der Signalleitung wird durch den gemessenen Frequenzgang in komplexer Form dargestellt.
Die zum Berechnen und Anzeigen von Daten verwendete Umgebung ist MATLAB R2015a.
Die folgenden auf der Website
www.StatEye.org veröffentlichten Beziehungen für die Version der StatEye 3.0-GUI-Methode [1, 2, 3] wurden als Beispiel für die Anfangsdaten verwendet.
Datenrate bps = 10,3125 Gbit / s. Die Zeitkonstanten des normalisierten Filters zweiter Ordnung sind gleich, ihr Kehrwert ist ¾ der Datenübertragungsfrequenz. Die Signalleitung wird durch einen Frequenzgang dargestellt. Die Charakteristik wurde bei Kanal f = 0,006495: 0,0012475: 20 GHz gemessen. Die angegebene Anzahl von Abtastpunkten der Fourier-Transformation: Punkte = 2 ^ 13.
Abbildung 1 zeigt die in diesem Dokument diskutierten Datenübertragungs-, Sequenz- und Datenverarbeitungsergebnisse. Der Übergang vom Zeitbereich zum Frequenzbereich und umgekehrt erfolgt mit dem Fast Fourier Transform (FFT) -Algorithmus.
Abbildung 1. Datenkanal. Eingangssignal iSignal.Tx, Ausgangssignal des Filters iSignal.Filter_out, Ausgangssignalleitung iSignal.Rx. Die im Diagramm gezeigten Eigenschaften werden unten diskutiert.Berechnungssequenz
In dieser Arbeit werden die Hauptberechnungen im Frequenzbereich durchgeführt. Hierzu wurde das ursprüngliche Signal aus dem Zeitbereich unter Verwendung der Fourier-Transformation in den Frequenzbereich übertragen. Durch Multiplizieren der spektralen Eigenschaften des Signals, des Filters und der Signalleitung wurde das Ausgangssignal des Pfades gefunden, das durch die inverse Fourier-Transformation vom Frequenzbereich in den Zeitbereich übertragen wird.
Die Datenübertragungsrate ist doppelt so hoch wie die Frequenz, mit der Daten übertragen werden. Die maximale Frequenz der gemessenen Signalleitung max (Kanal.f) = 20 GHz. Bei dieser Frequenz können Daten mit einer Geschwindigkeit von 40 Gbit / s (als 2 * max (Kanal.f)) übertragen werden.
Die maximale Datenübertragungsrate, die die maximale Übertragungsrate auf der Signalleitung von 40 Gbit / s und eine Mehrfachübertragungsrate von bps = 10,3125 Gbit / s nicht überschreitet, beträgt fmax = 30,9375 Gbit / s, die Multiplizität N = 3 (N = fmax / bps). Ferner wird fmax als Grenzfrequenz zum Berechnen der Antwort des Signals unter Verwendung der Fourier-Transformation verwendet.
Übersetzung des Eingangssignals in den Frequenzbereich
Zeitdiskriminierung zum Aufbau des Eingangssignals (Datenbit) im Zeitbereich Ts = 1 / fmax; Ts = 3,232e-11 s. Normalisiert in Bezug auf die Signaldauer besteht die Zeitskala aus 2 ^ 13 Punkten (Punkten), die Skala enthält das folgende Array von Punkten Zeit = bps / Ts. * (1: Punkte). Ein diskretes Einzelsignal mit einer Übertragungsrate von bps = 10,3125 Gbit / s und einer Quantisierung mit einer Periode Ts = 1 / fmax besteht aus drei Punkten im Bereich von 10 bis 11 Einheiten normalisierter Zeit. Ein Signal mit Einheitsamplitude kann an einer anderen Stelle auf der Timeline erstellt werden. Es ist jedoch besser, von den Rändern zurückzutreten, um den Hintergrund und den Übergangsprozess des Ausgangssignals vollständig zu sehen. Ein Impulssignal (Datenbit), das mit den folgenden MATLAB-Befehlen erstellt wurde, ist in Abbildung 2 dargestellt.
iSignal.Tx(1:size(time,2)) = 0; t0 = max(find(time<=10)); t1 = max(find(time<11)); iSignal.Tx(t0:t1) = 1.0;
Abbildung 2. Eingangsimpulssignal iSignal.Tx, Datenbit.Die Übersetzung des iSignal.Tx-Signals in den Frequenzbereich wird durch die folgenden FFT-Funktionen durchgeführt.
iSignal.shiftedPSD = fft(iSignal.Tx); iSignal.PSD = fftshift(iSignal.shiftedPSD);
Die Fourier-Transformationsfunktion fft konstruiert ein symmetrisches Spektrum des Signals in den Bereichen positiver und negativer Frequenzen, deren maximale Frequenz in der Mitte des Spektrums liegt (siehe Abbildung 3). Die fftshift-Funktion stellt das Spektrum wieder her, indem die Nullfrequenz des Signals wie in Abbildung 4 gezeigt in die Mitte verschoben wird.
Die Auflösung der Spektrumsfrequenz beträgt fs = fmax / Punkte; Die Frequenzfrequenzen reichen von -fmax / 2 bis fmax / 2-fs und sind gleich f = -fmax / 2: fs: fmax / 2-fs;
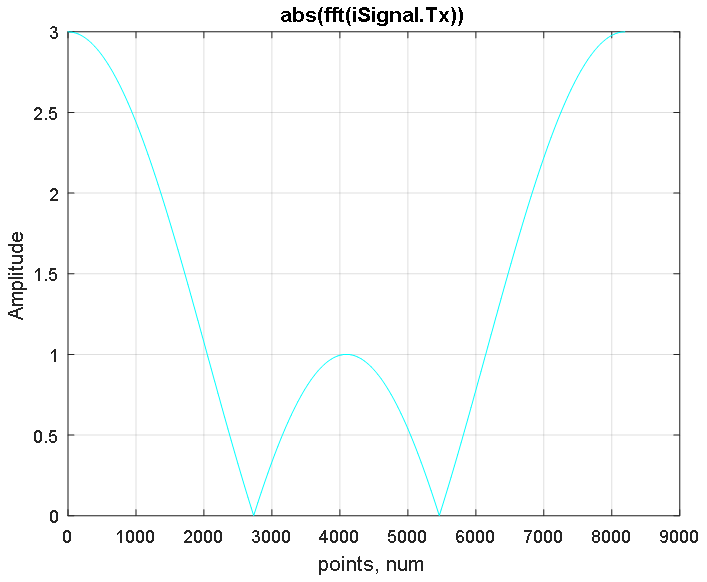Abbildung 3. Amplitudenantwort des verschobenen Spektrums des mit der FFT erhaltenen iSignal.Tx-Signals.
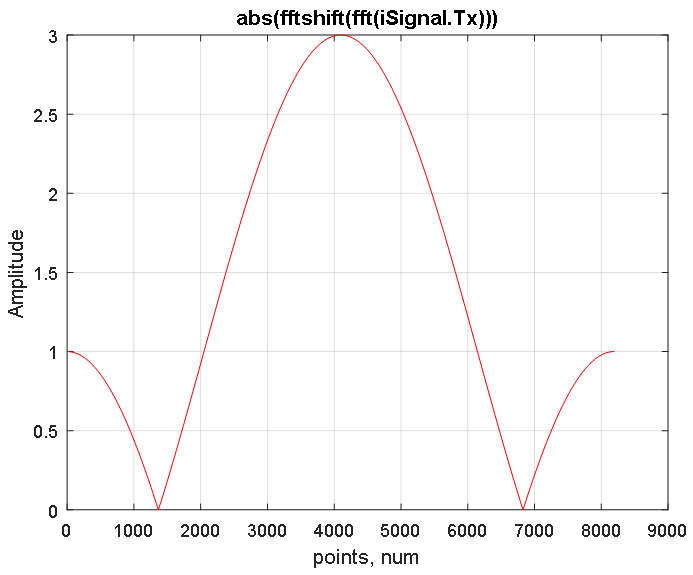Abbildung 4. Amplitudenantwort des rekonstruierten Spektrums des in Abbildung 3 gezeigten iSignal.Tx-Signals. 2 ^ 13 Beispiele werden vorgestellt. Die durchschnittliche Anzahl bei 4097 entspricht der Frequenz Null. Negative Frequenzen befinden sich auf der linken Seite (von 1 bis 4096 Punkten) und der Bereich der positiven Frequenzen auf der rechten Seite (von 4098 bis 8192 Punkten).Übertragungsfunktion des normalisierten Tiefpassfilters
In diesem Beispiel hat die Übertragungsfunktion des Filters zweiter Ordnung die Form
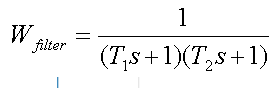
wobei T1 und T2 Filterzeitkonstanten sind. Die Frequenzen 1 / T1 sind gleich und 1 / T2 werden relativ zu der Frequenz eingestellt, mit der die Daten übertragen werden: 1 / T1 = 1 / T2 = 0,75 * bps (bps = 10,3125 Gbit / s).
Normalisierte Filterbandbreite
f_nrm =fmax/bps/points.*(-points/2:points/2-1).
Betreiber
s = f_nrm .* j;
Die Amplitudenphasenkennlinie des normalisierten Filters für positive und negative Frequenzen, die in Bezug auf die Signalübertragungsfrequenz normalisiert sind, ist in 5 gezeigt. Die logarithmische Amplitudenfrequenzkennlinie des Filters ist in 6 gezeigt.
Abbildung 5. Die Amplituden-Phasen-Charakteristik eines normalisierten Filters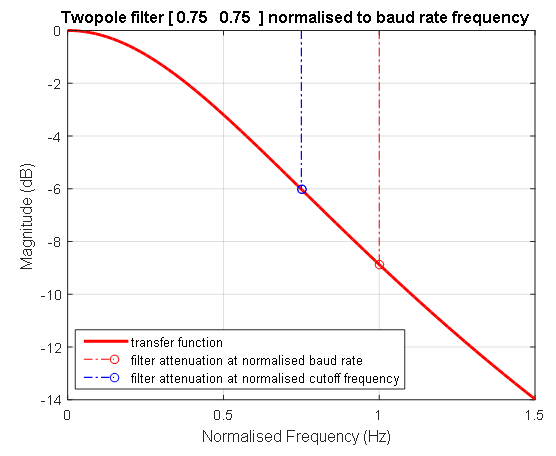
Abbildung 6. Logarithmischer Amplituden-Phasen-Frequenzgang eines normalisierten Filters. Die blaue gestrichelte Linie zeigt die Position der Filterfrequenz mit einem Wert von 0,75 der Frequenz, mit der Daten übertragen werden. Bei dieser Frequenz (1 / T1 = 1 / T2) beträgt der Transmissionskoeffizient des Filters zweiter Ordnung -6 Dezibel. Die rote gestrichelte Linie zeigt die Einheitsfrequenz an, mit der Daten übertragen werden.Übersetzung der Messergebnisse der Signalleitung in die Art der Übertragungsfunktion
Die gemessene Amplituden-Phasen-Charakteristik der Signalleitung umfasst 1599 Abtastwerte im Band bis 20 GHz mit einem festen Schritt von 12,475 MHz. Es enthält die folgenden Frequenzwerte: channel.f = 0,006495: 0,0012475: 20 GHz. Anfangs wurde die Signalleitung durch eine Kennlinie mit vier Anschlüssen dargestellt. Diese Eigenschaft wurde transformiert und wird im Beispiel als eindimensionale komplexe Funktion verwendet.
Die als Ergebnis der Messung erhaltenen charakteristischen Signalleitungsfrequenzen stimmen nicht mit den Frequenzen des Eingangssignalspektrums überein, die ein Vielfaches der Datenübertragungsfrequenz sind. Außerdem enthält das Signalleitungsspektrum nur positive Frequenzen und keine Frequenzen im Nullbereich. Das Eingangssignalspektrum enthält positive, Null- und negative Frequenzen.
Um die Eigenschaften der Signalleitung in eine Übertragungsfunktion umzuwandeln - eine Eigenschaft, deren Frequenzen mit den Frequenzen des Spektrums des Eingangssignals übereinstimmen, werden die folgenden Schritte ausgeführt.
1. Die Berechnung der Amplitude der Eigenschaften der Linie bei einer Frequenz von Null durch Extrapolation. Hierzu werden aus zehn Punkten der Amplitudenkennlinie, die der Frequenz Null am nächsten liegen, die Koeffizienten eines linearen Polynoms gefunden, die sich der Amplitudenkennlinie annähern:
[a] = polyfit(channel.f(1:10), channel.abs(1:10), 1);
Der zweite gefundene Polynomkoeffizient ist gleich der Amplitude der Charakteristik bei einer Frequenz von Null:
channel.dc = a(2);
2. Die Phasenantwort bei einer Frequenz von Null wird gleich Null genommen.
channel.dcPhase = 0.00;
3. Die Neuberechnung der Amplitudenkanal- und Phasenkanalphaseneigenschaften der Signalleitung mit Werten bei einer Frequenz von Null wird an der Frequenz des Eingangssignalspektrums (f = -fmax / 2: fmax / Punkte: fmax / 2-fmax / Punkte) mit Extrapolation der Eigenschaften auf durchgeführt Bereich von Null und negativen Frequenzen:
ichannel.abs = interp1([0 channel.f], [channel.dc channel.abs], abs(f), 'linear', 'extrap'); ichannel.phase = interp1([0 channel.f], [channel.dcPhase unwrap(channel.phase)], abs(f), 'linear', 'extrap'); ichannel.s = ichannel.abs .* exp(+j.*ichannel.phase); ichannel.tf = real(ichannel.s) + j*imag(ichannel.s) .* sign(f);
Die erhaltene Übertragungsfunktion - der Amplituden-Phasen-Frequenzgang des Kanals im Niederfrequenzbereich ist in Abbildung 7 dargestellt. Die Amplituden-Frequenz-Eigenschaften der gemessenen Signalleitung und die berechnete Übertragungsfunktion in den vollen Frequenzbereichen sind in Abbildung 8 dargestellt. Die gleichen Eigenschaften im Phasenraum sind in Abbildung 9 dargestellt.
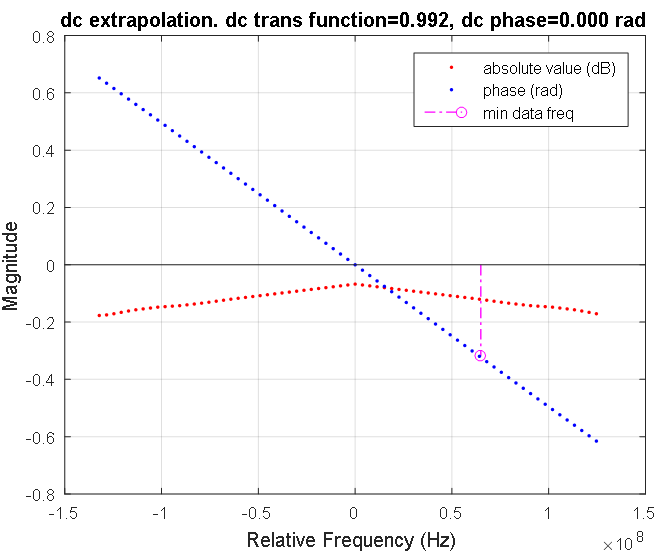Abbildung 7. Die Übertragungsfunktion der Signalleitung im Niederfrequenzbereich. Rote und blaue Punkte zeigen diskrete Amplituden- bzw. Phaseneigenschaften an. Die Amplitudenantwort wird in Dezibel angegeben, die Phase im Bogenmaß. Die rosa Linie markiert die niedrigste Frequenz der gemessenen Charakteristik der Signalleitung. Der Übertragungskoeffizient bei einer Frequenz von Null beträgt 0,992.
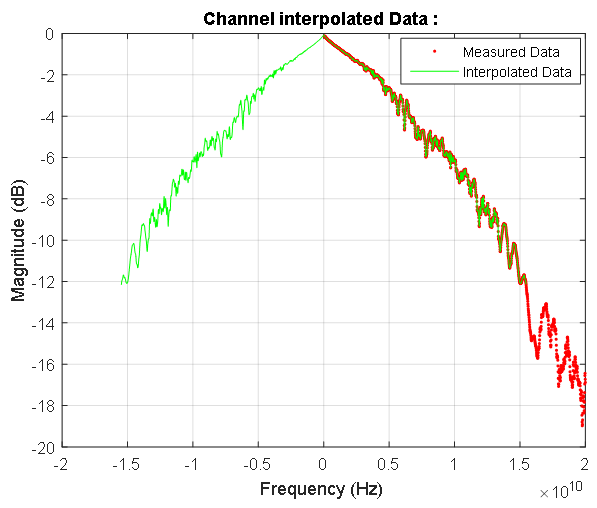Abbildung 8. Frequenzgang der Signalleitung. Blaue Punkte zeigen die komplexen Daten der gemessenen Linie an. Die berechnete symmetrische Abhängigkeit der Signalleitungsverstärkung bei den Frequenzen des Eingangssignalspektrums ist rot hervorgehoben. Im Nullfrequenzbereich ist diese Charakteristik in Abbildung 7 dargestellt.
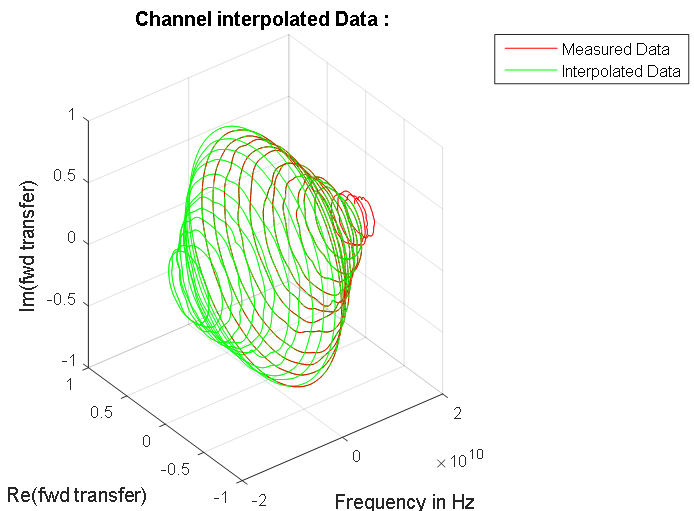Abbildung 9. Amplitudenphasenfrequenzkennlinien der gemessenen Datenleitung und ihres normalisierten Spektrums.Berechnung der Signalantwort
Die Antwort (Antwort auf den Eingangseffekt) im Frequenzbereich wird erhalten, indem das Spektrum des Signals mit dem Produkt der Übertragungsfunktionen der Elemente multipliziert wird, die die Reaktion auf das Eingangssignal beziehen. In unserem Fall passiert das Signal das Filter und die Signalleitung.
Die inverse Fourier-Transformation ifft wird verwendet, um das Signal vom Frequenzbereich in den Zeitbereich zu übertragen.
Die Filterausgabe im Zeitbereich iSignal.Filter_out wird berechnet als
TransFunction.PSD = iSignal.PSD .* Filter.PSD_Tx; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Filter_out = real(ifft(TransFunction.shiftedPSD));
Das Ausgangssignal der iSignal.Rx-Leitung ist gleich dem Produkt aus dem Spektrum des Eingangssignals und den Übertragungsfunktionen des Filters und der Signalleitung mit der anschließenden Übertragung des empfangenen Signals vom Frequenzbereich in den Zeitbereich.
TransFunction.PSD = TransFunction.PSD .* ichannel.tf; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Rx = real(ifft(TransFunction.shiftedPSD));
Die Reaktion des Filters auf den idealen Eingangsimpuls und die Reaktion des Kanals sind in Abbildung 10 dargestellt.
Abbildung 10. Filterausgabe (rotes Diagramm) und Datenzeilenausgabe (grünes Diagramm). Filtereingangssignal - Ein einzelner Impuls ist in Abbildung 2 dargestellt. Der Signalleitungseingang ist das Filterausgangssignal.Anwendung. Verwendeter M-Code MATLAB
Bibliografische Liste
1. IEEE802.3ap. NRZ-Simulationsergebnisse mit 10,3125 Gbit / s unter Verwendung von „StatEye“ und „Signal-zu-Interferenz-Modell“ für kaskadierte Kanalkomponenten. Shannon Sawyer und Charles Moore / Agilent Technologies. 24. Januar 2005
www.ieee802.org/3/ap/public/jan05/sawyer_01_0105.pdf2. Was ist StatEye? IEEE 803.3ap Task Force. 16. September 2004
www.ieee802.org/3/ap/public/signal_adhoc/ghiasi_01_0904.pdf3. Stat Eye / IBM-Vereinbarung. Steve Anderson. Xilinx, Inc.
www.ieee802.org/3/ap/public/nov04/anderson_01_1104.pdf