Nachhaltigkeits-GAN-Training

Die GAN-Idee wurde erstmals von Jan Goodfellow Generative Adversarial Nets, Goodfellow et al. 2014 , veröffentlicht. Danach sind GANs eines der besten generativen Modelle.

Wie bei jedem anderen generativen Modell besteht die GAN-Aufgabe darin, ein Datenmodell zu erstellen und insbesondere zu lernen, wie Stichproben aus einer Verteilung generiert werden, die so nah wie möglich an der Datenverteilung liegt (normalerweise gibt es einen Datensatz mit begrenzter Größe, die Datenverteilung, in der wir modellieren möchten).

GANs haben eine Vielzahl von Vorteilen, aber einen wesentlichen Nachteil: Sie sind sehr schwer zu trainieren.

Kürzlich wurde eine Reihe von Arbeiten zur Nachhaltigkeit von GAN veröffentlicht:

• Die GAN-Optimierung für Gradientenabstieg ist lokal stabil, Vaishnavh Nagarajan, J. Zico Kolter, 2017
• Die Numerik der GANs, Lars Mescheder et al., 2017

Inspiriert von ihren Ideen habe ich ein wenig recherchiert.

Ich habe versucht, den Text so einfach wie möglich zu gestalten und wenn möglich nur die einfachste Mathematik zu verwenden. Um zu rechtfertigen, warum wir die Eigenschaften zweidimensionaler Vektorfelder berücksichtigen können, müssen wir leider ein wenig in Richtung der Variationsrechnung graben. Wenn jemand mit diesen Begriffen nicht vertraut ist, können Sie sofort mit der Betrachtung zweidimensionaler Vektorfelder für verschiedene GAN-Typen fortfahren.

Wir werden nun versuchen, unter die Haube des Trainingsverfahrens zu schauen und zu verstehen, was dort passiert.

GAN, das Hauptproblem

GANs bestehen aus zwei neuronalen Netzen: einem Diskriminator und einem Generator. Generator - Ermöglicht das Abtasten einer Verteilung (normalerweise als Verteilung des Generators bezeichnet). Der Diskriminator empfängt Eingangsabtastwerte aus dem Originaldatensatz und dem Generator und lernt vorherzusagen, woher diese Stichprobe stammt (Datensatz oder Generator).

GAN-Schema:



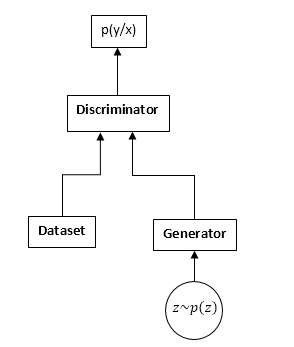
Der GAN-Schulungsprozess ist wie folgt:

1. Wir nehmen n Proben aus dem Datensatz und m Proben aus dem Generator.
2. Wir korrigieren die Generatorgewichte und aktualisieren die Diskriminatorparameter. Dies ist eine häufige Klassifizierungsaufgabe. Wir müssen den Diskriminator nur bis zur Konvergenz nicht trainieren. Und noch öfter stört es auch.
3. Wir korrigieren die Diskriminatorgewichte und aktualisieren die Generatorgewichte, sodass der Diskriminator zu glauben beginnt, dass unsere Stichproben aus dem Datensatz und nicht aus dem Generator stammen.
4. Wir wiederholen 1-3, bis der Diskriminator und der Generator ins Gleichgewicht kommen (das heißt, keiner der anderen kann den anderen „täuschen“).

Wir werden den GAN-Lernprozess nicht im Detail untersuchen. Im Internet und insbesondere im HubR gibt es viele Artikel, die diesen Prozess ausführlich erläutern.

Wir werden uns für etwas ganz anderes interessieren. Aufgrund der Tatsache, dass wir mit zwei neuronalen Netzen konkurrieren, hört die Aufgabe nämlich auf, nach einem Minimum (Maximum) zu suchen, sondern verwandelt sich in bestimmten Fällen in eine Suche nach einem Sattelpunkt (d. H. In den Schritten 2 und 3 versuchen wir dieselbe Funktion Maximieren durch Diskriminatorparameter und Minimieren durch Generatorparameter), und in den allgemeineren Schritten 2 und 3 können wir völlig unterschiedliche Funktionen optimieren. Offensichtlich ist das Minimax-Problem ein Sonderfall der Optimierung verschiedener Funktionen - eine Funktion wird mit unterschiedlichen Vorzeichen genommen.

Schauen wir uns das in den Formeln an. Wir nehmen an, dass pd (x) die Verteilung ist, von der der Datensatz abgetastet wird, pg (x) die Verteilung des Generators ist, D (x) die Ausgabe des Diskriminators ist.

Wenn wir einen Diskriminator trainieren, maximieren wir häufig solche Funktionen:

$$

$$J \ = \ \ int {p_d (x) log (D (x)) dx \ + \ \ int {p_g (x) log (1 \ - \ D (x)) dx}}$$

Farbverlaufsvektor:

$$

$$v = \ \ nabla_ \ theta J \ = \ int {\ frac {p_d (x)} {D (x)} \ nabla_ \ theta D (x) \ dx \ + \ \ int {\ frac {p_g (x )} {1 \ - \ D (x)} \ nabla_ \ theta D (x) dx}}$$

Beim Training des Generators maximieren wir:

$$

$$I \ = \ - \ int {p_g (x) log (1 \ - \ D (x)) dx}$$

Der Gradientenvektor in diesem Fall:

$$

$$u \ = \ \ nabla_ \ varphi I \ = \ - \ int {{\ nabla_ \ varphi p} _g (x) log (1 \ - \ D (x)) dx}$$

In Zukunft werden wir sehen, dass die Funktionen jeweils ersetzt werden können durch:

$$

$$J \ = \ \ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ = \ \ int {p_g (x) f_3 (D (x)) dx}$$

Wo $$$f_1, f_2, f_3$ werden nach bestimmten Regeln ausgewählt. Übrigens verwendet Ian Goodfellow in seinem Originalartikel $$$f_1 und f_2$ wie beim Training eines regulären Diskriminators, und $$$f_3$ wählt, um die Steigungen in der Anfangsphase des Trainings zu verbessern:

$$

$$f_1 \ left (x \ right) = log \ left (x \ right), \ f_2 \ left (x \ right) = log \ left (1 \ - \ x \ right), f_3 \ left (x \ right) = log \ left (x \ right)$$

Auf den ersten Blick scheint die Aufgabe der üblichen Aufgabe des Lernens mit Gradientenabstieg (Aufstieg) sehr ähnlich zu sein. Warum waren sich dann alle, die auf GAN-Training stießen, einig, dass es so verdammt schwer war?

Die Antwort liegt in der Struktur des Vektorfeldes, mit dem wir die Parameter neuronaler Netze aktualisieren. Im Fall des üblichen Klassifizierungsproblems verwenden wir nur den Gradientenvektor, d. H. Das Feld ist potentiell (die optimierte Funktion selbst ist das Potential dieses Vektorfeldes). Und potenzielle Vektorfelder haben einige bemerkenswerte Eigenschaften, von denen eine das Fehlen geschlossener Kurven ist. Das heißt, es ist unmöglich, auf diesem Gebiet im Kreis zu laufen. Wenn jedoch GAN trainiert wird, ist das gesamte Vektorfeld trotz der Tatsache, dass die Vektorfelder für den Generator und den Diskriminator getrennt potentiell sind (die gleichen sind Gradienten), nicht potentiell. Und dies bedeutet, dass es in diesem Feld geschlossene Kurven geben kann, d. H. Wir können im Kreis gehen. Und das ist sehr, sehr schlecht.

Es stellt sich die Frage: Warum schaffen wir es trotzdem, das GAN recht erfolgreich zu trainieren, vielleicht ist das Feld immer noch irrotational (potenziell)? Und wenn ja, warum ist es dann so kompliziert?
Ich werde leider weitermachen, das Feld ist nicht potenziell, aber es hat eine Reihe guter Eigenschaften. Leider reagiert das Feld auch sehr empfindlich auf die Parametrisierung neuronaler Netze (Auswahl der Aktivierungsfunktionen, Verwendung von DropOut, BatchNormalization usw.). Aber das Wichtigste zuerst.

GAN-Feld "Gradient"

Wir werden die GAN-Lernfunktionen in der allgemeinsten Form betrachten:

$$

$$J \ = \ \ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ = \ \ int {p_g (x) f_3 (D (x)) dx}$$

Wir müssen beide Funktionen gleichzeitig optimieren. Unter der Annahme, dass D (x) und pg (x) absolut flexible Funktionen sind, d.h. Wir können an jedem Punkt eine beliebige Zahl nehmen, unabhängig von anderen Punkten. Das ist eine bekannte Tatsache aus der Variationsrechnung - Sie müssen die Funktion in Richtung der Variationsableitung dieser Funktion ändern (im Allgemeinen ein vollständiges Analogon des Gradientenanstiegs).

Wir schreiben die Variationsableitung:

$$

$$\ frac {\ partielles J} {\ partielles D (x)} = p_d (x) f_1 '(D (x)) \ + \ p_g (x) f_2' (D (x))$$

$$

$$\ frac {\ partielles I} {\ partielles p_g (x)} = f_3 (D (x))$$

Wir werden nur die erste Funktion (für den Diskriminator) betrachten, für die zweite wird alles gleich sein.

Aber wenn man bedenkt, dass wir die Funktion tatsächlich nur in der Reihe von Funktionen ändern können, die durch unser neuronales Netzwerk dargestellt werden können, werden wir schreiben:

$$$$ Anzeige $$ ∆D (x) = \ frac {\ Teil D (x)} {\ Teil θ_j} Δθ_j $$ Anzeige $$

Änderungen der Netzwerkparameter, im Allgemeinen der übliche Gradientenabstieg (Anstieg):

$$$$ Anzeige $$ ∆θj = \ frac {\ partielle J} {\ partielle θ_j} μ $$ Anzeige $$

µ ist die Lernrate. Nun, die Ableitung in Bezug auf die Netzwerkparameter:

$$

$$\ frac {\ partielles J} {\ partielles \ theta_j} = \ int {\ frac {\ partielles J} {\ partielles D (y)} \ frac {\ partielles D (y)} {\ partielles \ theta_j} dy }$$

Und jetzt setzen wir alles zusammen:

$$

$$∆D (x) = \ sum_ {j} {\ frac {\ partielles D (x)} {\ partielles \ theta_j} \ int {\ frac {\ partielles J} {\ partielles D (y)} \ frac { \ partielles D (y)} {\ partielles \ theta_j} dy} \ mu \ = \ mu \ int \ frac {\ partielles J} {\ partielles D (y)}} \ sum_ {j} {\ frac {\ partielles D (x)} {\ partiell \ theta_j} \ frac {\ partiell D (x)} {\ partiell \ theta_j} dy \ = \} \ mu \ int {\ frac {\ partiell J} {\ partiell D (y )} K_ \ theta (x, y) dy}$$

Wo: $$$K_ \ theta (x, y) \ = \ sum_ {j} {\ frac {\ partielles D (x)} {\ partielles \ theta_j} \ frac {\ partielles D (x)} {\ partielles \ theta_j} \ }$

Ich habe diese Funktion in der Literatur zum maschinellen Lernen noch nie gesehen, daher werde ich sie den parametrischen Kern des Systems nennen.

Nun, oder wenn wir zu kontinuierlichen Zeitschritten gehen (von Differenzgleichungen zu Differentialgleichungen), erhalten wir:

$$

$$\ frac {d} {dt} D (x) \ = \ \ int {\ frac {\ partielles J} {\ partielles D (y)} K_ \ theta (x, y) dy}$$

Diese Gleichung zeigt die interne Beziehung des ursprünglichen Feldes (punktweise für den Diskriminator) und die Parametrisierung des neuronalen Netzwerks. Wir erhalten eine völlig ähnliche Gleichung für den Generator.

Angesichts der Tatsache, dass K (x, y) (der parametrische Kernel) eine positive bestimmte Funktion ist (nun, wie kann es als Skalarprodukt von Gradienten an den entsprechenden Punkten dargestellt werden), können wir schließen, dass alle Änderungen der trainierten Funktionen (Diskriminator und Generator) zum Hilbert-Raum gehören erzeugt durch den Kern, d.h. K (x, y). Ich frage mich, ob es hier möglich ist, aussagekräftige Ergebnisse zu erzielen. Aber wir werden noch nicht in diese Richtung schauen, sondern in die andere.

Wie Sie sehen können, wird die Stabilität des GAN durch zwei Komponenten bestimmt: die Variationsableitungen der Funktionalen und die Parametrisierung des neuronalen Netzwerks. Unsere Aufgabe ist es zu sehen, wie sich dieses Feld punktuell verhält, dh ob unser Netzwerk absolut jede Funktion darstellen kann. Die Aufgabe wird zu einer Analyse eines zweidimensionalen Vektorfeldes. Und das liegt meiner Meinung nach in unserer Macht.

Nachhaltigkeit

Wir betrachten also das folgende Vektorfeld:

$$

$$\ frac {d} {dt} D (x) = \ \ frac {\ partielles J} {\ partielles D (x)}$$

$$

$$\ frac {d} {dt} p_g (x) = \ \ frac {\ partielles I} {\ partielles p_g (x)}$$

Offensichtlich können diese Gleichungen nur für einen Punkt x betrachtet werden, wobei berücksichtigt wird, wie unsere Variationsableitungen aussehen:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ prime (D) \ + \ p_gf_2 ^ \ prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D)$$

Die erste Voraussetzung für dieses Gleichungssystem ist, dass die rechte Seite auf 0 gehen muss, wenn:
$$$p_d = p_g$

Andernfalls werden wir versuchen, das Modell zu trainieren, was offensichtlich nicht zur richtigen Lösung konvergiert. Das heißt, D muss eine Lösung für die folgende Gleichung sein:

$$

$$f_1 ^ \ prime (D) \ + \ f_2 ^ \ prime (D) \ = \ 0$$

Wir bezeichnen diese Lösung als $$$D0$ .

Angesichts der Tatsache, dass pg (x) die Wahrscheinlichkeitsdichte auf der rechten Seite ist, können wir eine beliebige Zahl hinzufügen, ohne die Ableitungen zu verletzen. Subtrahieren Sie den Wert in t, um 0 von der rechten Seite am gewünschten Punkt bereitzustellen. $$$D0$ (Dies muss getan werden, wenn wir pg punktweise betrachten wollen - den Übergang von einem durch Wahrscheinlichkeitsdichten parametrisierten Feld zu freien Feldern).

Als Ergebnis erhalten wir das folgende Feld:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ prime (D) \ + \ p_gf_2 ^ \ prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D) \ - \ f (D0)$$

Von nun an werden wir die Ruhepunkte und die Stabilität der Felder dieser Art untersuchen.
Wir können zwei Arten von Stabilität untersuchen: lokal (in der Nähe des Ruhepunkts) und global (unter Verwendung der Lyapunov-Funktionsmethode).

Um die lokale Stabilität zu untersuchen, muss die Jacobi-Matrix des Feldes berechnet werden.
Damit das Feld lokal „stabil“ ist, müssen die Eigenwerte einen negativen Realteil haben.

Verschiedene Arten von GAN

1. Klassisches GAN

   
   
   In der klassischen GAN verwenden wir regulären Logloss:
   

   $$

   $$J \ = \ \ int {p_d (x) log (D (x)) dx \ + \ \ int {p_g (x) log (1 \ - \ D (x)) dx}}$$
   
   Für das Training des Diskriminators ist es notwendig, ihn zu maximieren, für den Generator, ihn zu minimieren. In diesem Fall sieht das Feld folgendermaßen aus:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ -log (1-D) \ + \ log (\ frac {1} {2})$$
   
   Mal sehen, wie sich die Parameter (pg und D) in diesem Bereich entwickeln werden. Verwenden Sie dazu dieses einfache Python-Skript:
   
   
   Skript

   def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = -np.log(1.-d) + np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
   Als Ausgangspunkt $$$p_g = 0,9, D = 0,25$ es wird so aussehen:
   
   
   
   Der Ruhepunkt eines solchen Feldes ist: pg = pd und D = 0,5
   
   Man kann leicht überprüfen, ob die Realteile der Eigenwerte der Jacobi-Matrix negativ sind, d. H. Das Feld ist lokal stabil.
   Wir werden uns nicht mit dem Beweis globaler Nachhaltigkeit befassen. Wenn es jedoch sehr interessant ist, können Sie mit dem Python-Skript herumspielen und sicherstellen, dass das Feld für alle gültigen Anfangswerte stabil ist.

2. Modifikation von Jan Goodfellow

   
   Wir haben bereits oben besprochen, dass Ian Goodfellow im Originalartikel eine leicht modifizierte Version von GAN verwendet hat. Für seine Version waren die Funktionen wie folgt:
   

   $$

   $$f_1 \ left (x \ right) = log \ left (x \ right), \ f_2 \ left (x \ right) = log \ left (1 \ - \ x \ right), f_3 \ left (x \ right) = log \ left (x \ right)$$
   
   Das Feld sieht folgendermaßen aus:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ log (D) \ - \ log (\ frac {1} {2})$$
   
   Das Python-Skript ist das gleiche, nur die Feldfunktion ist unterschiedlich:
   
   
   Skript

    def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = np.log(d) - np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
   Und mit den gleichen Anfangsdaten sieht das Bild folgendermaßen aus:
   
   
   
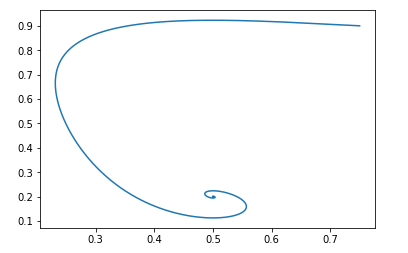
   Auch hier ist es einfach zu überprüfen, ob das Feld lokal stabil ist.
   Das heißt, unter dem Gesichtspunkt der Konvergenz beeinträchtigt eine solche Modifikation die Eigenschaften des GAN nicht, hat jedoch ihre eigenen Vorteile hinsichtlich des Trainings neuronaler Netze.

3. Wasserstein gan

   
   Schauen wir uns eine andere beliebte Ansicht von GAN an. Die optimierte Funktionalität sieht folgendermaßen aus:
   

   $$

   $$J \ = \ \ int {p_d (x) D (x) dx \ - \} \ int {p_g (x) D (x) dx}$$
   
   Wobei D zur Klasse der 1-Lipschitz-Funktionen in Bezug auf x gehört.
   Wir wollen es um D maximieren und um pg minimieren.
   
   In diesem Fall natürlich: $$$f_1 \ left (x \ right) = x, \ f_2 \ left (x \ right) = - x, \ f_3 \ left (x \ right) = x$
   
   Und das Feld wird so aussehen:
   

   $$

   $$\ frac {d} {dt} D = \ p_d \ - {\ p} _g \ $$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ D$$
   
   In diesem Feld kann ein Kreis mit einem Mittelpunkt an einem Punkt leicht erraten werden. $$$p_g = p_d, D = 0$ .
   Das heißt, wenn wir dieses Feld entlang gehen, werden wir immer im Kreis herumlaufen.
   
   Hier ist ein Beispiel für einen Pfad in einem solchen Feld:
   
   
   
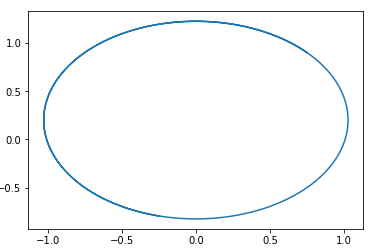
   Die Frage ist, warum es sich dann herausstellt, diese Art von GAN zu trainieren. Die Antwort ist sehr einfach - diese Analyse berücksichtigt nicht die Tatsache der 1-Lipschitz-Eigenschaft von D. Das heißt, wir können keine willkürlichen Funktionen übernehmen. Dies stimmt übrigens gut mit den Ergebnissen der Autoren ... des Artikels überein. Um nicht im Kreis zu laufen, empfehlen sie, den Diskriminator auf Konvergenz zu trainieren: Wasserstein GAN

4. Neue GAN-Optionen

   
   Funktionsauswahl $$$f_1, f_2 und f_3$ Sie können verschiedene GAN-Optionen erstellen. Die Hauptanforderung für diese Funktionen besteht darin, das Vorhandensein eines „richtigen“ Ruhepunkts und die Stabilität dieses Punktes (vorzugsweise global, aber zumindest lokal) sicherzustellen. Ich gebe dem Leser die Möglichkeit, die Einschränkungen für die Funktionen f1, f2 und f3 abzuleiten, die für die lokale Stabilität erforderlich sind. Es ist einfach - betrachten Sie einfach die quadratische Gleichung für die Eigenwerte der Jacobi-Matrix.
   
   Ich werde ein Beispiel für eine solche GAN geben:
   

   $$

   $$f_1 (x) \ = \ -0,5x ^ 2, \ f_2 (x) \ = \ x, \ f_3 (x) \ = \ -x$$
   
   Ich schlage erneut vor, dass der Leser selbst das Feld dieses GAN aufbaut und seine Stabilität beweist. (Übrigens ist dies eines der wenigen Felder, für die der Nachweis der globalen Stabilität elementar ist - wählen Sie einfach die Lyapunov-Funktion, den Abstand zum Ruhepunkt). Berücksichtigen Sie einfach, dass der Ruhepunkt D = 1 ist.

Schlussfolgerung und weitere Forschung

Aus der obigen Analyse ist ersichtlich, dass alle klassischen GANs (mit Ausnahme des Wassertein-GAN, das über eigene Methoden zur Verbesserung der Stabilität verfügt) „gute“ Felder aufweisen. Das heißt, Das Folgen dieser Felder hat einen einzelnen Ruhepunkt, an dem die Verteilung des Generators gleich der Verteilung der Daten ist.

Warum ist es dann so schwierig, GAN zu trainieren? Die Antwort ist einfach - Parametrisierung neuronaler Netze. Mit einer „schlechten“ Parametrierung können wir auch im Kreis spazieren gehen. Zum Beispiel zeigen meine Experimente, dass zum Beispiel die Verwendung von BatchNormalization in einem der Netzwerke das Feld sofort in ein geschlossenes verwandelt. Und die Relu-Aktivierung funktioniert am besten.

Leider gibt es derzeit keine einzige Möglichkeit, theoretisch zu überprüfen, welche Elemente des neuronalen Netzwerks das Feld ändern können. Es wird sich für mich als prospektiv erweisen, die Eigenschaften des parametrischen Kernels des Systems zu untersuchen - $$$K_ \ theta (x, y)$ .

Ich wollte auch über Möglichkeiten zur Regularisierung von GAN-Feldern sprechen und dies aus der Perspektive zweidimensionaler Felder betrachten. Betrachten Sie die Reinforcement Learning-Algorithmen aus dieser Perspektive. Und vieles mehr. Leider stellte sich heraus, dass der Artikel sowieso zu groß war, also dazu ein anderes Mal mehr.