Tiefe neuronale Netze haben zu einem Durchbruch bei vielen Bilderkennungsaufgaben wie Computer Vision und Spracherkennung geführt. Das Faltungs-Neuronale Netz ist eine der beliebtesten Arten von Neuronalen Netzen.
Grundsätzlich kann ein Faltungs-Neuronales Netzwerk als ein Neuronales Netzwerk betrachtet werden, das viele identische Kopien desselben Neurons verwendet. Dies ermöglicht dem Netzwerk eine begrenzte Anzahl von Parametern bei der Berechnung großer Modelle.
 2D-Faltungs-Neuronales Netz
2D-Faltungs-Neuronales NetzDiese Technik mit mehreren Kopien desselben Neurons hat eine enge Analogie zur Abstraktion von Funktionen in Mathematik und Informatik. Während der Programmierung wird die Funktion einmal geschrieben und dann wiederverwendet, ohne dass Sie denselben Code mehrmals an verschiedenen Stellen schreiben müssen, was die Ausführung des Programms beschleunigt und die Anzahl der Fehler verringert. In ähnlicher Weise verwendet ein Faltungs-Neuronales Netzwerk, sobald es ein Neuron trainiert hat, es an vielen Stellen, was das Modelltraining erleichtert und Fehler minimiert.
Die Struktur von Faltungs-Neuronalen Netzen
Angenommen, es wird eine Aufgabe angegeben, bei der anhand des Audios vorhergesagt werden muss, ob die Audiodatei die Stimme einer Person enthält.
Am Eingang erhalten wir Audio-Samples zu verschiedenen Zeitpunkten. Die Proben sind gleichmäßig verteilt.

Der einfachste Weg, sie mit einem neuronalen Netzwerk zu klassifizieren, besteht darin, alle Samples mit einer vollständig verbundenen Schicht zu verbinden. In diesem Fall ist jeder Eingang mit jedem Neuron verbunden.
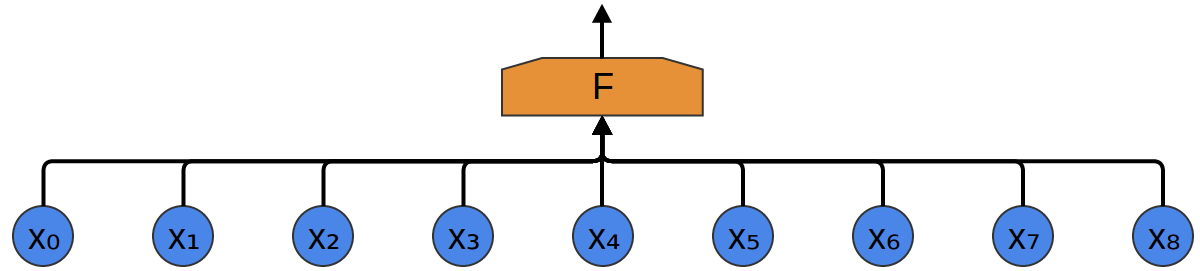
Ein komplexerer Ansatz berücksichtigt eine gewisse Symmetrie in den Eigenschaften, die in den Daten enthalten sind. Wir achten sehr auf die lokalen Eigenschaften der Daten: Wie hoch ist die Schallfrequenz für eine bestimmte Zeit? Zunehmend oder abnehmend? Usw.
Wir berücksichtigen jederzeit die gleichen Eigenschaften. Es ist nützlich, die Frequenzen am Anfang, in der Mitte und am Ende zu kennen. Beachten Sie, dass dies lokale Eigenschaften sind, da Sie nur ein kleines Audiosequenzfenster benötigen, um sie zu definieren.
Somit ist es möglich, eine Gruppe von Neuronen A zu erstellen, die kleine Zeitabschnitte in unseren Daten berücksichtigen. A betrachtet alle diese Segmente und berechnet bestimmte Funktionen. Dann wird der Ausgang dieser Faltungsschicht in eine vollständig verbundene Schicht F eingespeist.
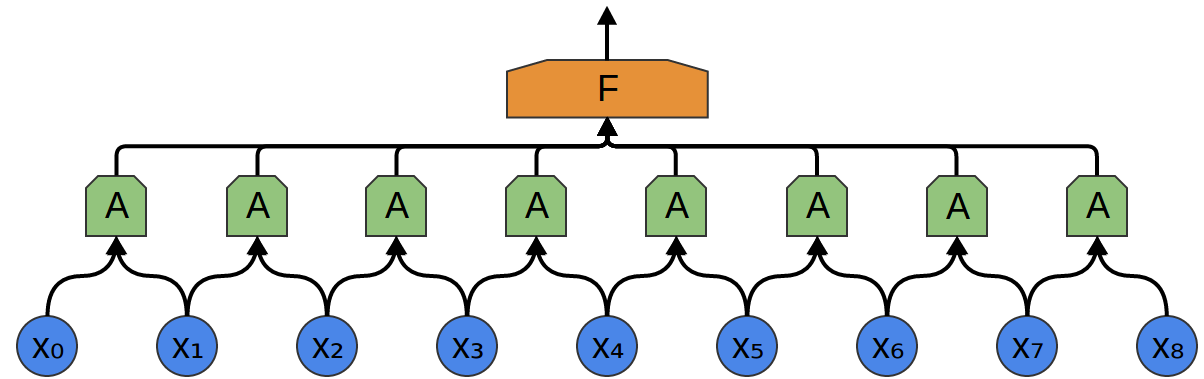
Im obigen Beispiel hat A nur Zweipunktsegmente verarbeitet. Dies ist in der Praxis selten. Normalerweise ist das Faltungsschichtfenster viel größer.
Im folgenden Beispiel empfängt A 3 Segmente am Eingang. Dies ist auch für reale Aufgaben unwahrscheinlich, aber leider ist es schwierig, A zu visualisieren, das mehrere Eingänge verbindet.
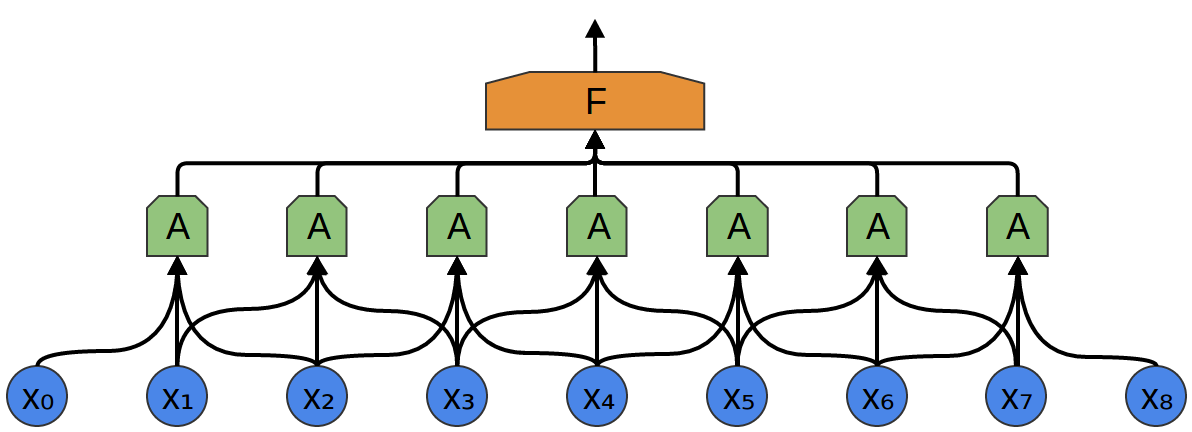
Eine schöne Eigenschaft von Faltungsschichten ist, dass sie zusammengesetzt sind. Sie können die Ausgabe einer Faltungsschicht einer anderen zuführen. Mit jeder Schicht entdeckt das Netzwerk höhere, abstraktere Funktionen.
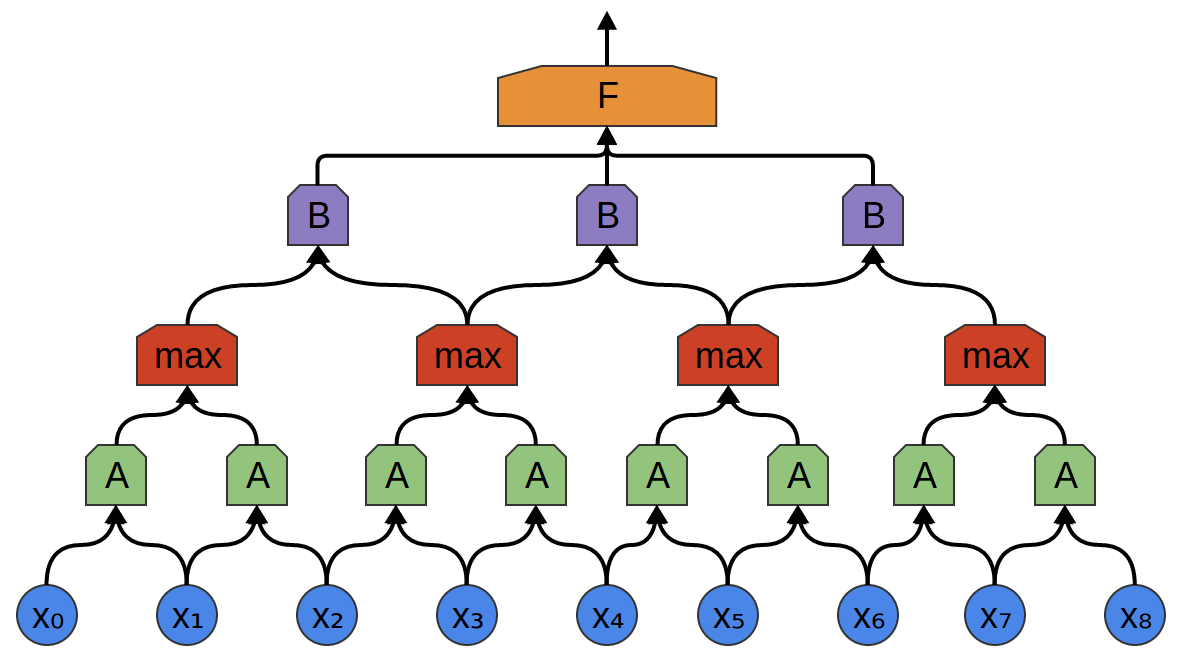
Im folgenden Beispiel gibt es eine neue Gruppe von Neuronen B. B wird verwendet, um eine weitere Faltungsschicht zu erzeugen, die über der vorherigen liegt.
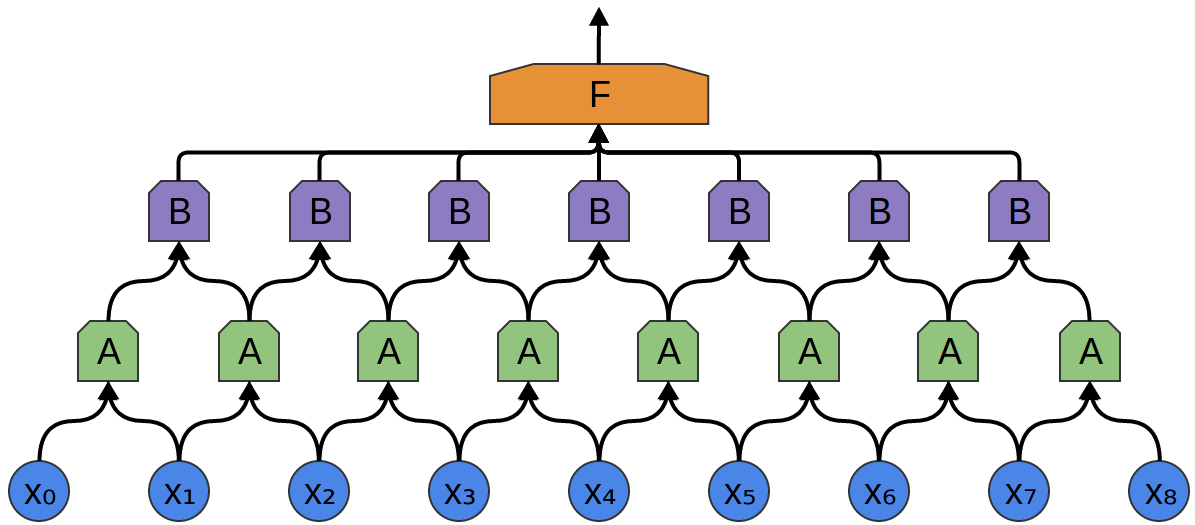
Faltungsschichten werden häufig durch Bündeln (Kombinieren) von Schichten miteinander verflochten. Insbesondere gibt es eine Art Schicht namens Max-Pooling, die äußerst beliebt ist.
Oft ist es uns egal, wann genau ein nützliches Signal in den Daten vorhanden ist. Ist es wichtig, ob sich die Signalfrequenz früher oder später ändert?
Max-Pooling absorbiert maximale Funktionen aus kleinen Blöcken des vorherigen Levels. Die Schlussfolgerung besagt, ob das gewünschte Funktionssignal in der vorherigen Schicht vorhanden war, aber nicht genau wo.
Max-Pooling-Schichten - dies ist eine "Abnahme". Es ermöglicht späteren Faltungsschichten, große Datenmengen zu bearbeiten, da die kleinen Patches nach der Zusammenführungsschicht dem viel größeren Patch davor entsprechen. Sie machen uns auch für einige sehr kleine Datentransformationen unveränderlich.
In unseren vorherigen Beispielen wurden eindimensionale Faltungsschichten verwendet. Faltungsschichten können jedoch mit umfangreicheren Daten arbeiten. Tatsächlich verwenden die bekanntesten Lösungen, die auf Faltungs-Neuronalen Netzen basieren, zweidimensionale Faltungs-Neuronale Netze zur Mustererkennung.
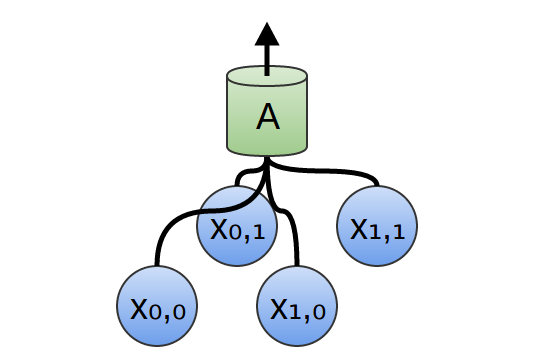
In einer zweidimensionalen Faltungsschicht betrachtet A nicht Segmente, sondern Patches.
Für jeden Patch berechnet A die Funktion. Zum Beispiel kann sie lernen, das Vorhandensein einer Kante oder Textur oder den Kontrast zwischen zwei Farben zu erkennen.
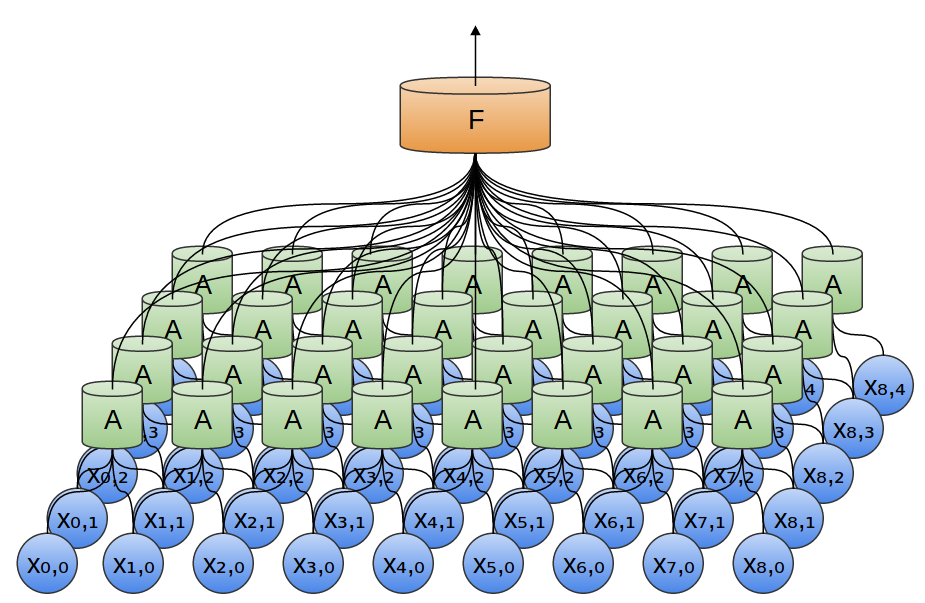
Im vorherigen Beispiel wurde die Ausgabe der Faltungsschicht in eine vollständig verbundene Schicht eingespeist. Es ist jedoch möglich, zwei Faltungsschichten zusammenzusetzen, wie dies im betrachteten eindimensionalen Fall der Fall war.

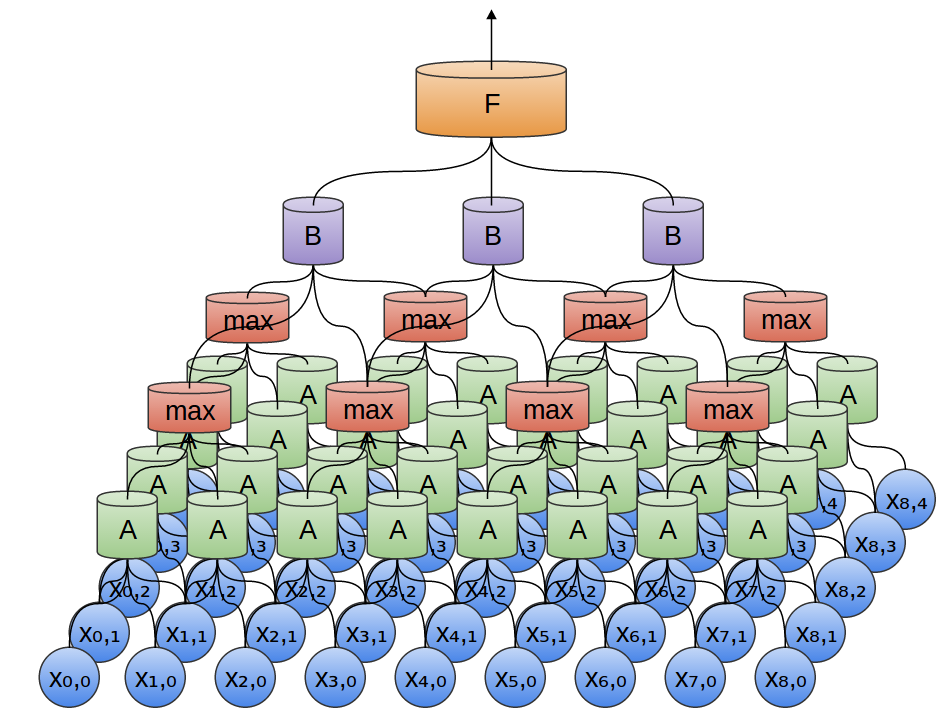
Wir können Max-Pooling auch in zwei Dimensionen durchführen. Hier nehmen wir das Maximum an Funktionen aus einem kleinen Patch.
Dies läuft darauf hinaus, dass bei Betrachtung des gesamten Bildes die genaue Position der Kante bis zum Pixel nicht wichtig ist. Es reicht zu wissen, wo es sich innerhalb weniger Pixel befindet.
Außerdem werden manchmal dreidimensionale Faltungsnetzwerke für Daten wie Video- oder Massendaten verwendet (z. B. 3D-Scannen in der Medizin). Solche Netzwerke sind jedoch nicht sehr verbreitet und viel schwieriger zu visualisieren.
Früher haben wir gesagt, dass A eine Gruppe von Neuronen ist. Wir werden genauer darauf eingehen: Was ist A?
In traditionellen Faltungsschichten ist A ein paralleles Bündel von Neuronen, alle Neuronen empfangen die gleichen Eingangssignale und berechnen unterschiedliche Funktionen.
Beispielsweise kann in einer zweidimensionalen Faltungsschicht ein Neuron horizontale Kanten, ein anderes vertikale Kanten und einen dritten grün-roten Farbkontrast erfassen.
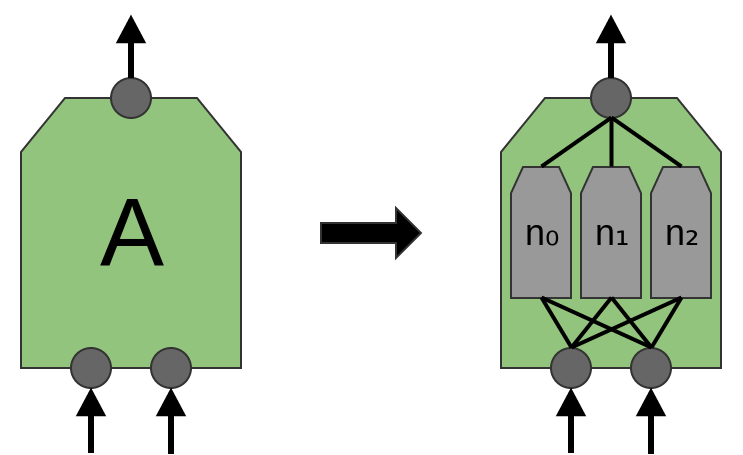
Der Artikel 'Network in Network' (Lin et al. (2013)) schlägt eine neue Ebene vor, "Mlpconv". In diesem Modell hat A mehrere Ebenen von Neuronen, wobei die letzte Schicht Funktionen höherer Ebenen für die behandelte Region ableitet. In dem Artikel erzielt das Modell beeindruckende Ergebnisse und setzt in einer Reihe von Referenzdatensätzen ein neues technologisches Niveau.
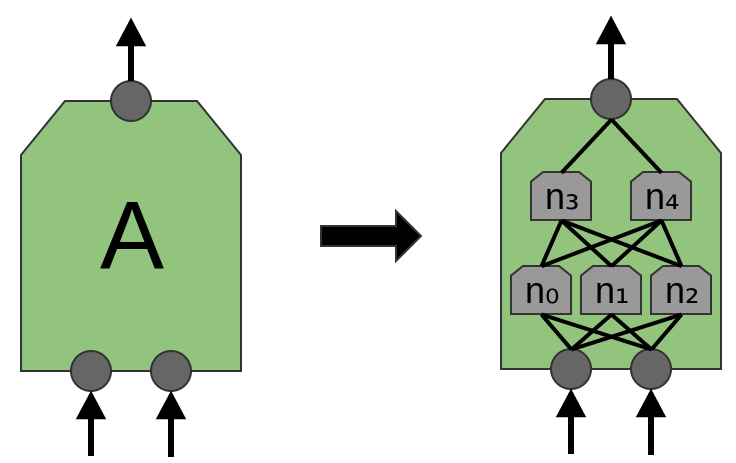
Für die Zwecke dieser Veröffentlichung konzentrieren wir uns auf Standard-Faltungsschichten.
Ergebnisse des Faltungs-Neuronalen Netzes
Im Jahr 2012 erzielten Alex Krizhevsky, Ilya Sutskever und Geoff Hinton eine signifikante Verbesserung der Erkennungsqualität im Vergleich zu den damals bekannten Lösungen (Krizehvsky et al. (2012)).
Fortschritt war das Ergebnis der Kombination mehrerer Ansätze. Grafikprozessoren wurden verwendet, um ein großes (nach den Standards von 2012) tiefes neuronales Netzwerk zu trainieren. Ein neuer Neuronentyp (ReLU) und eine neue Technik wurden verwendet, um das Problem der „Überanpassung“ (DropOut) zu reduzieren. Wir haben einen großen Datensatz mit einer großen Anzahl von Bildkategorien (ImageNet) verwendet. Und natürlich war es ein Faltungsnetzwerk.
Die unten gezeigte Architektur war tief. Es hat 5 Faltungsschichten, 3 abwechselnde Pooling- und drei vollständig verbundene Schichten.
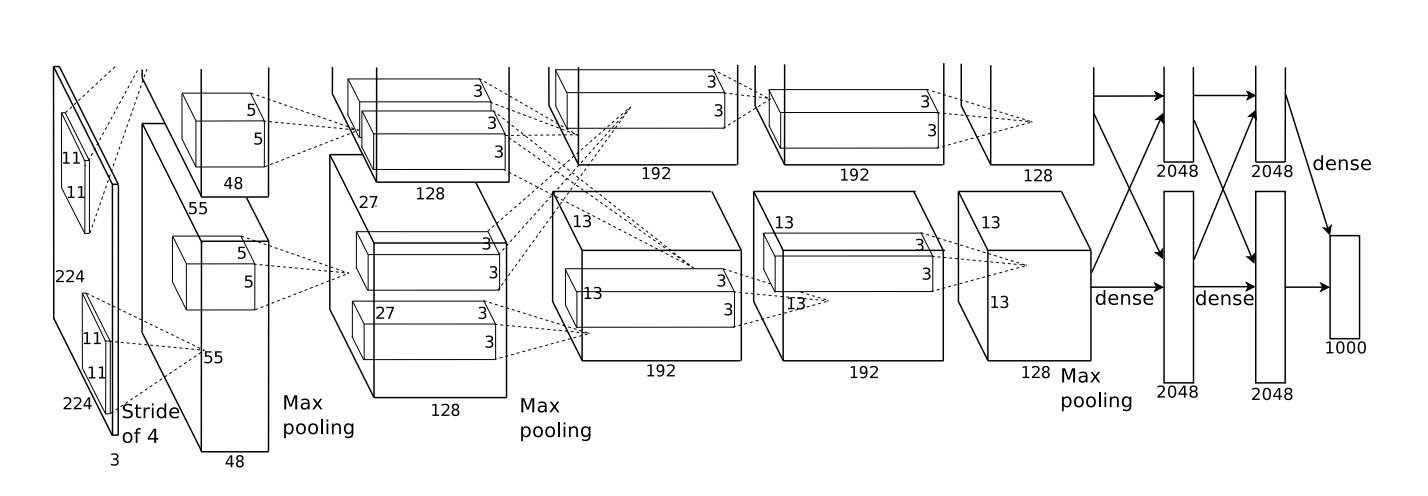
Von Krizehvsky et al. (2012)
Das Netzwerk wurde geschult, um Fotos in Tausende verschiedener Kategorien einzuteilen.
Das Modell von Krizhevsky et al. Konnte in 63% der Fälle die richtige Antwort geben. Darüber hinaus gibt es bei der richtigen Antwort aus den 5 besten Antworten 85% der Prognosen!

Lassen Sie uns veranschaulichen, was die erste Ebene des Netzwerks erkennt.
Denken Sie daran, dass die Faltungsschichten auf zwei GPUs aufgeteilt wurden. Informationen gehen nicht über jede Ebene hin und her. Es stellt sich heraus, dass sich beide Seiten bei jedem Start des Modells spezialisieren.

Filter erhalten durch die erste Faltungsschicht. Die obere Hälfte entspricht einer Schicht auf einer GPU, die untere Hälfte auf der anderen. Von Krizehvsky et al. (2012)
Neuronen auf einer Seite konzentrieren sich auf Schwarzweiß und lernen, Kanten unterschiedlicher Ausrichtung und Größe zu erkennen. Neuronen hingegen sind auf Farbe und Textur spezialisiert und erkennen Farbkontraste und -muster. Denken Sie daran, dass Neuronen zufällig initialisiert werden. Keine einzige Person hat sie als Grenzdetektoren eingesetzt oder auf diese Weise aufgeteilt. Dies geschah während des Trainings des Bildklassifizierungsnetzwerks.
Diese bemerkenswerten Ergebnisse (und andere aufregende Ergebnisse zu dieser Zeit) waren nur der Anfang. Es folgten schnell viele andere Arbeiten, die modifizierte Ansätze testeten und die Ergebnisse schrittweise verbesserten oder in anderen Bereichen anwendeten.
Faltungs-Neuronale Netze sind ein wichtiges Werkzeug für die Bildverarbeitung und die moderne Mustererkennung.
Formalisierung von Faltungs-Neuronalen Netzen
Betrachten Sie eine eindimensionale Faltungsschicht mit Eingaben {xn} und Ausgaben {yn}:
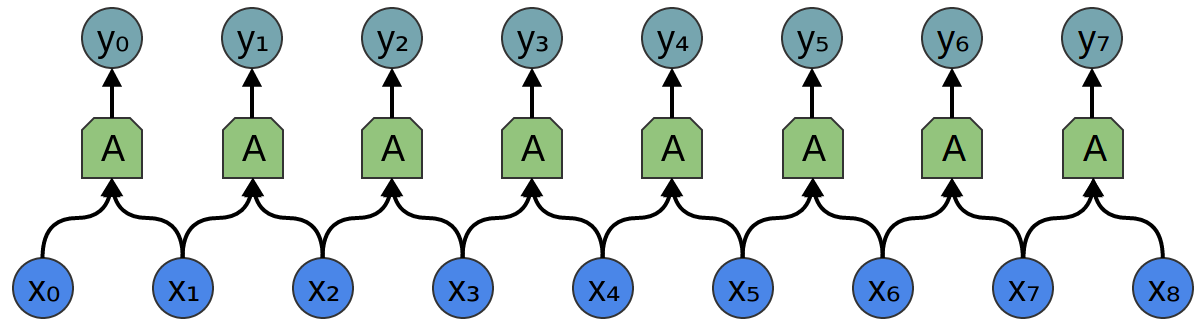
Es ist relativ einfach, die Ergebnisse in Bezug auf die Eingabe zu beschreiben:
yn = A (x, x + 1, ...)
Zum Beispiel im obigen Beispiel:
y0 = A (x0, x1)
y1 = A (x1, x2)
Wenn wir eine zweidimensionale Faltungsschicht mit Eingaben {xn, m} und Ausgaben {yn, m} betrachten:
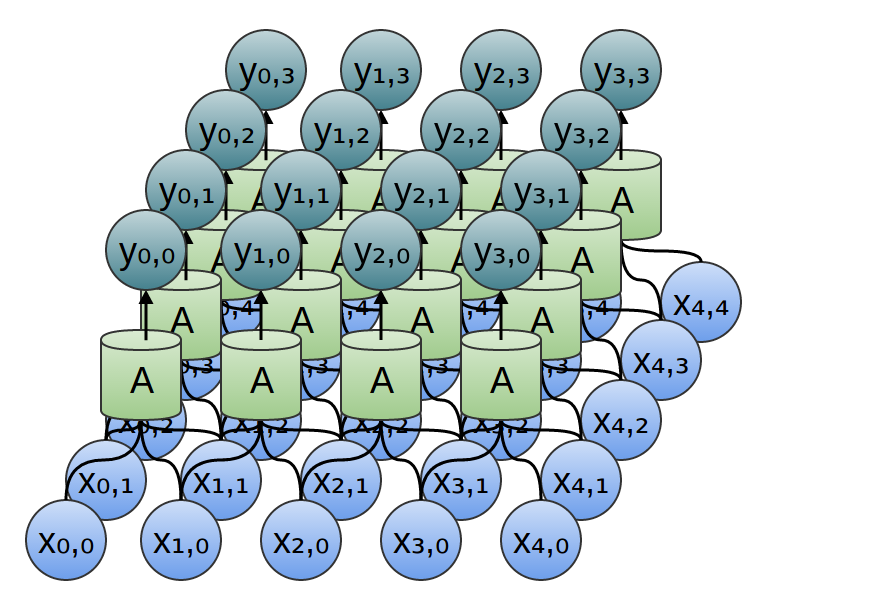
Das Netzwerk kann durch eine zweidimensionale Wertematrix dargestellt werden.
Fazit
Die Faltungsoperation ist ein mächtiges Werkzeug. In der Mathematik entsteht die Faltungsoperation in verschiedenen Kontexten, von der Untersuchung partieller Differentialgleichungen bis zur Wahrscheinlichkeitstheorie. Teilweise aufgrund seiner Rolle bei der PDE ist die Faltung in den Naturwissenschaften wichtig. Die Faltung spielt auch in vielen Anwendungsbereichen eine wichtige Rolle, beispielsweise in der Computergrafik und der Signalverarbeitung.