Seit vielen Jahren beobachte ich Snooker als Sport. Es hat alles: die faszinierende Schönheit eines intellektuellen Spiels, die Eleganz von Kiem-Schlägen und die psychologische Spannung des Wettbewerbs. Aber eines gefällt mir nicht - das Bewertungssystem .
Der Hauptnachteil besteht darin, dass nur die Tatsache der Turnierleistung berücksichtigt wird, ohne die „Komplexität“ der Spiele zu berücksichtigen. Dem Elo-Modell wird dieser Nachteil vorenthalten, der die „Stärke“ der Spieler überwacht und sie abhängig von den Ergebnissen der Spiele und der „Stärke“ des Gegners aktualisiert. Es passt jedoch nicht perfekt: Es wird angenommen, dass alle Spiele unter gleichen Bedingungen ausgetragen werden und im Snooker bis zu einer bestimmten Anzahl gewonnener Frames (Partys) gespielt werden. Um dieser Tatsache Rechnung zu tragen, habe ich ein anderes Modell in Betracht gezogen, das ich EloBeta nannte.
Dieser Artikel untersucht die Qualität von Elo- und EloBet-Modellen basierend auf den Ergebnissen von Snooker-Matches. Es ist wichtig anzumerken, dass die Hauptziele darin bestehen, die "Stärke" der Spieler zu bewerten und eine "faire" Bewertung zu erstellen, anstatt Vorhersagemodelle für die Erzielung von Gewinn zu erstellen.

Die aktuelle Snooker-Bewertung basiert auf den Erfolgen des Spielers bei Turnieren mit unterschiedlichem „Gewicht“. Es war einmal, dass nur Weltmeisterschaften berücksichtigt wurden. Nach dem Erscheinen vieler anderer Wettbewerbe wurde eine Punktetabelle erstellt, die der Spieler verdienen konnte, wenn er eine bestimmte Phase des Turniers erreichte. Jetzt hat die Bewertung die Form eines "bewegenden" Betrags an Preisgeld, den der Spieler in den (ungefähr) letzten zwei Kalenderjahren verdient hat.
Dieses System hat zwei Hauptvorteile: Es ist einfach (viel Geld gewinnen - in der Rangliste aufsteigen) und vorhersehbar (wenn Sie an einen bestimmten Ort aufsteigen möchten - einen bestimmten Geldbetrag gewinnen, alle anderen Dinge sind gleich). Das Problem ist, dass bei dieser Methode die Stärke (Geschicklichkeit, Form) der Gegner nicht berücksichtigt wird . Das übliche Gegenargument lautet: „Wenn ein Spieler das späte Stadium des Turniers erreicht hat, ist er per Definition der derzeitige starke Spieler“ („schwache Spieler gewinnen keine Turniere“). Klingt ziemlich überzeugend. Beim Snooker sollte jedoch wie bei jeder Sportart die Rolle des Falls berücksichtigt werden: Wenn ein Spieler „schwächer“ ist, bedeutet dies nicht, dass er / sie in einem Spiel gegen einen Spieler niemals „stärker“ gewinnen kann. Es kommt nur seltener vor als im umgekehrten Szenario. Hier kommt das Elo-Modell ins Spiel.
Die Idee des Elo-Modells ist, dass jedem Spieler eine numerische Bewertung zugeordnet ist. Es wird die Annahme eingeführt, dass das Ergebnis eines Spiels zwischen zwei Spielern anhand der unterschiedlichen Bewertungen vorhergesagt werden kann: Höhere Werte bedeuten eine höhere Wahrscheinlichkeit, einen „starken“ Spieler (mit einer höheren Bewertung) zu gewinnen. Die Elo-Bewertung basiert auf der aktuellen "Stärke" , die auf der Grundlage der Ergebnisse von Spielen mit anderen Spielern berechnet wird. Dies vermeidet einen größeren Fehler im aktuellen offiziellen Bewertungssystem. Mit diesem Ansatz können Sie auch die Spielerbewertung während des Turniers aktualisieren, um numerisch auf seine gute Leistung zu reagieren.
Aufgrund seiner praktischen Erfahrung mit Elo-Bewertungen scheint es mir, dass er sich im Snooker gut zeigen sollte. Es gibt jedoch ein Hindernis: Es ist für Wettbewerbe mit einer einzigen Art von Spiel konzipiert . Natürlich gibt es Variationen, um die Vorteile des Heimfeldes im Fußball und den ersten Schachzug zu berücksichtigen (beide in Form einer festen Anzahl von Bewertungspunkten für den Spieler mit einem Vorteil). Beim Snooker werden Spiele im "Best of N" -Format gespielt: Der Spieler, der die ersten gewinnt, gewinnt n = f r a c N + 1 2 Frames (Parteien). Wir werden dieses Format auch "bis" nennen n Siege. "
Intuitiv sollte es für einen „schwachen“ Spieler schwieriger sein, ein Match mit bis zu 10 Siegen (Finale eines ernsthaften Turniers) zu gewinnen, als ein Match mit 4 Siegen (erste Runde der aktuellen Home Nations-Turniere). Dies wird in meinem EloBet-Modell berücksichtigt.
Die Idee, die Elo-Bewertung im Snooker zu verwenden, ist keineswegs neu. Zum Beispiel gibt es die folgenden Arbeiten:
- Snooker Analyst verwendet ein Elo-ähnliches Bewertungssystem (eher ein Bradley-Terry-Modell ). Die Idee ist, die Bewertung basierend auf der Differenz zwischen der "echten" und der "erwarteten" Anzahl der gewonnenen Frames zu aktualisieren. Dieser Ansatz wirft Fragen auf. Natürlich zeigt der größere Unterschied in der Anzahl der Frames höchstwahrscheinlich den größeren Unterschied in der Stärke, aber anfangs hat der Spieler keine solche Aufgabe. Beim Snooker ist das Ziel "nur", das Match zu gewinnen, d.h. Gewinne eine bestimmte Anzahl von Frames vor dem Gegner.
- Diese Diskussion findet im Forum mit der Implementierung des grundlegenden Elo-Modells statt.
- Dies und das sind echte Anwendungen im Amateur-Snooker.
- Vielleicht gibt es andere Werke, die ich vermisst habe. Für Informationen zu diesem Thema wäre ich sehr dankbar.
Rückblick
Dieser Artikel richtet sich an Benutzer der R- Sprache, die die Bewertung von Elo studieren möchten, und an Snooker-Fans. Alle Experimente sind mit der Idee geschrieben, reproduzierbar zu sein. Der Code ist unter Spoilern versteckt, enthält Kommentare und verwendet Tidyverse- Pakete. Daher kann es für Benutzer interessant sein, R selbst zu lesen. Es wird davon ausgegangen, dass der gesamte dargestellte Code nacheinander ausgeführt wird. Eine Datei finden Sie hier .
Der Artikel ist wie folgt aufgebaut:
- Der Abschnitt Modell beschreibt die Ansätze von Elo und EloBet mit Implementierung in R.
- Der Abschnitt Experiment beschreibt die Details und die Motivation der Berechnung: Welche Daten und Methoden werden verwendet (und warum) und welche Ergebnisse werden erzielt.
- Der Abschnitt EloBet-Ranking-Studie enthält die Ergebnisse der Anwendung des EloBet-Modells auf echte Snooker-Daten. Er wird sich mehr für Snooker-Liebhaber interessieren.
Wir benötigen die folgende Initialisierung.
Initialisierungscode# suppressPackageStartupMessages(library(dplyr)) library(tidyr) library(purrr) # library(ggplot2) # suppressPackageStartupMessages(library(comperank)) theme_set(theme_bw()) # . . set.seed(20180703)
Modelle
Beide Modelle basieren auf folgenden Annahmen:
- Es gibt eine feste Gruppe von Spielern, die von „am stärksten“ (erster Platz) bis „am schwächsten“ (letzter Platz) eingestuft werden müssen.
- Rangliste nach Spielerverband ich mit numerischer Bewertung r i : Eine Zahl, die die "Stärke" des Spielers darstellt (ein höherer Wert bedeutet einen stärkeren Spieler).
- Je größer der Unterschied in den Bewertungen vor dem Spiel ist, desto weniger wahrscheinlich ist der Sieg des „schwachen“ Spielers (mit einer niedrigeren Bewertung).
- Die Bewertungen werden nach jedem Spiel basierend auf dem Ergebnis und den Bewertungen vor dem Spiel aktualisiert.
- Ein Sieg über einen Gegner "stärker" sollte mit einer größeren Erhöhung der Bewertung einhergehen als ein Sieg über einen Gegner "schwächer". Bei einer Niederlage ist das Gegenteil der Fall.
Elo
Elo-Modellcode #' @details . #' `...` . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). #' . elo_win_prob <- function(rating1, rating2, ksi = 400, ...) { norm_rating_diff <- (rating2 - rating1) / ksi 1 / (1 + 10^norm_rating_diff) } #' @return , #' `comperank::add_iterative_ratings()`. elo_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { comperank::elo(rating1, score1, rating2, score2, K = K, ksi = ksi)[1, ] } }
Elo Model aktualisiert die Bewertungen wie folgt:
Berechnung der Wahrscheinlichkeit, dass ein bestimmter Spieler das Spiel gewinnt (bevor es beginnt). Die Wahrscheinlichkeit, dass ein Spieler mit der Kennung gewinnt (wir nennen ihn / sie "zuerst") ich und bewertet r i über einen anderen Spieler ("Sekunde") mit Kennung j und bewertet r j gleich
P r ( r i , r j ) = f r a c 1 1 + 10 ( r j - r i ) / 400
Bei diesem Ansatz folgt die Wahrscheinlichkeitsberechnung der dritten Annahme.
Das Normalisieren der Differenz auf 400 ist eine mathematische Methode, um zu sagen, welche Differenz als "groß" angesehen wird. Diese Nummer kann durch einen Modellparameter ersetzt werden. x i Dies wirkt sich jedoch nur auf die Verbreitung zukünftiger Ratings aus und ist in der Regel überflüssig. Ein Wert von 400 ist ziemlich Standard.
Bei einem allgemeinen Ansatz ist die Wahrscheinlichkeit eines Sieges gleich L ( r j - r i ) wo L ( x ) Einige streng ansteigende Funktionen mit Werten von 0 bis 1. Wir werden die logistische Kurve verwenden. Eine vollständigere Studie finden Sie in diesem Artikel .
Match-Ergebnisberechnung S. . Im Basismodell entspricht es 1 bei einem Sieg des ersten Spielers (Niederlage des zweiten Spielers), 0,5 bei einem Unentschieden und 0 bei einer Niederlage des ersten Spielers (Sieg des zweiten Spielers).
Bewertungsaktualisierung :
- delta=K cdot(S−Pr(ri,rj)) . Dies ist der Betrag, um den sich die Bewertungen ändern. Sie verwendet einen Koeffizienten K (der einzige Parameter des Modells). Weniger K (mit gleichen Wahrscheinlichkeiten) bedeutet eine geringere Änderung der Bewertungen - das Modell ist konservativer, d.h. Weitere Siege sind erforderlich, um eine Veränderung der Stärke zu "beweisen". Auf der anderen Seite mehr K bedeutet mehr Glaubwürdigkeit bei aktuellen Ergebnissen als bei aktuellen Bewertungen. Die Wahl von "optimal" K ist ein Weg, um ein "gutes" Bewertungssystem zu schaffen .
- r(neu)i=ri+ delta , r(neu)j=rj− delta .
Anmerkungen :
- Wie aus den Aktualisierungsformeln hervorgeht, ändert sich die Summe der Bewertungen aller betrachteten Spieler im Laufe der Zeit nicht: Die Bewertung steigt aufgrund einer Abnahme der Bewertung des Gegners
- Spieler ohne gespielte Spiele sind mit einer Anfangsbewertung von 0 verbunden. Normalerweise werden Werte von 1500 oder 1000 verwendet, aber ich sehe keinen anderen Grund als einen psychologischen. Unter Berücksichtigung der vorherigen Bemerkung bedeutet die Verwendung von Null, dass die Summe aller Bewertungen immer Null ist, was auf seine Weise schön ist.
- Es ist notwendig, eine bestimmte Anzahl von Spielen zu spielen, damit die Bewertung die "Stärke" des Spielers widerspiegelt. Dies stellt ein Problem dar: Neu hinzugefügte Spieler beginnen mit einer Bewertung von 0, was wahrscheinlich nicht die kleinste unter den aktuellen Spielern ist. Mit anderen Worten, "Newcomer" gelten als "stärker" als einige andere Spieler. Sie können versuchen, dies mit externen Bewertungsaktualisierungsverfahren zu bekämpfen, wenn Sie einen neuen Spieler eingeben.
Warum ist ein solcher Algorithmus sinnvoll? Bei gleicher Bewertung delta immer gleich 0.5 cdotK . Nehmen wir zum Beispiel an, dass ri=0 und rj=400 . Dies bedeutet, dass die Wahrscheinlichkeit, den ersten Spieler zu gewinnen, gleich ist frac11+10 ca.0,0909 d.h. er / sie gewinnt 1 von 11 Spielen.
- Im Falle eines Sieges erhält er / sie eine Erhöhung von ungefähr 0.909 cdotK , was mehr ist als bei der Gleichheit der Ratings.
- Im Falle einer Niederlage erhält er / sie eine Ermäßigung von ungefähr 0.0909 cdotK Dies ist weniger als bei der Gleichheit der Ratings.
Dies zeigt, dass das Elo-Modell der fünften Annahme folgt: Ein Sieg über einen Gegner ist „stärker“, geht mit einer stärkeren Erhöhung der Bewertung einher als ein Sieg über einen Gegner „schwächer“ und umgekehrt.
Natürlich hat das Elo-Modell seine eigenen (ziemlich hochrangigen) praktischen Eigenschaften . Das Wichtigste für unsere Studie ist jedoch Folgendes: Es wird davon ausgegangen, dass alle Spiele gleichberechtigt ausgetragen werden. Dies bedeutet, dass die Distanz des Spiels nicht berücksichtigt wird: Ein Sieg in einem Spiel mit bis zu 4 Siegen wird genauso belohnt wie ein Sieg in einem Spiel mit bis zu 10 Siegen. Hier kommt das Bühnenmodell EloBeta.
EloBeta
EloBet-Modellcode #' @details . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). `frames_to_win` #' . #' . elobeta_win_prob <- function(rating1, rating2, frames_to_win, ksi = 400, ...) { prob_frame <- elo_win_prob(rating1 = rating1, rating2 = rating2, ksi = ksi) # , `frames_to_win` # # (`prob_frame`). . pbeta(prob_frame, frames_to_win, frames_to_win) } #' @return : 1 / #' (), 0.5 0 / (). get_match_result <- function(score1, score2) { # () , . near_score <- dplyr::near(score1, score2) dplyr::if_else(near_score, 0.5, as.numeric(score1 > score2)) } #' @return , #' `add_iterative_ratings()`. elobeta_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { prob_win <- elobeta_win_prob( rating1 = rating1, rating2 = rating2, frames_to_win = pmax(score1, score2), ksi = ksi ) match_result <- get_match_result(score1, score2) delta <- K * (match_result - prob_win) c(rating1 + delta, rating2 - delta) } }
Im Elo-Modell wirkt sich der Unterschied in den Bewertungen direkt auf die Wahrscheinlichkeit aus, das gesamte Spiel zu gewinnen. Die Hauptidee des EloBet-Modells ist der direkte Einfluss des Bewertungsunterschieds auf die Gewinnwahrscheinlichkeit in einem Frame und die explizite Berechnung der Gewinnwahrscheinlichkeit eines Spielers n Frames vor dem Gegner .
Die Frage bleibt: Wie berechnet man eine solche Wahrscheinlichkeit? Es stellt sich heraus, dass dies eines der ältesten Probleme in der Geschichte der Wahrscheinlichkeitstheorie ist und einen eigenen Namen hat - das Problem der Aufteilung von Wetten (Problem der Punkte). Eine sehr schöne Präsentation finden Sie in diesem Artikel . Unter Verwendung seiner Notation ist die gewünschte Wahrscheinlichkeit:
P(n,n)= sum limit2n−1j=n2n−1 wählejpj(1−p)2n−1−j
Hier P(n,n) - Wahrscheinlichkeit, dass der erste Spieler das Match zuvor gewinnt n Siege; p - die Wahrscheinlichkeit seines Sieges in einem Frame (der Gegner hat die Wahrscheinlichkeit 1−p ) Bei diesem Ansatz wird angenommen, dass die Rahmenergebnisse innerhalb der Übereinstimmung unabhängig voneinander sind . Dies mag zweifelhaft sein, ist jedoch eine notwendige Annahme für dieses Modell.
Gibt es eine schnellere Möglichkeit zur Berechnung? Es stellt sich heraus, dass die Antwort ja ist. Nach mehreren Stunden Formelkonvertierung, praktischen Experimenten und Internetrecherchen fand ich die folgende Eigenschaft bei einer regulierten unvollständigen Beta-Funktion Ix(a,b) . Ersetzen m=k, n=2k−1 in diese Eigenschaft und ersetzen k auf n es stellt sich heraus P(n,n)=Ip(n,n) .
Dies ist auch eine gute Nachricht für R-Benutzer, da Ip(n,n) kann als pbeta(p, n, n) berechnet werden. Hinweis : Der allgemeine Fall der Siegwahrscheinlichkeit in n Frames bevor der Gegner gewinnt m kann auch berechnet werden als Ip(n,m) bzw. pbeta(p, n, m) . Dies eröffnet großartige Möglichkeiten, die Gewinnwahrscheinlichkeit während des Spiels zu aktualisieren .
Das Bewertungsaktualisierungsverfahren im Rahmen des EloBet-Modells hat die folgende Form (mit bekannten Bewertungen ri und rj Anzahl der Frames, die benötigt werden, um zu gewinnen n und das Ergebnis des Spiels S , wie im Elo-Modell):
- Berechnung der Gewinnwahrscheinlichkeit des ersten Spielers in einem Frame : p=Pr(ri,rj)= frac11+10(rj−ri)/400 .
- Berechnung der Gewinnwahrscheinlichkeit dieses Spielers im Spiel : PrBeta(ri,rj)=Ip(n,n) . Zum Beispiel wenn p gleich 0,4, dann sinkt die Wahrscheinlichkeit, das Match vor 4 Siegen zu gewinnen, auf 0,29 und in "auf 18 Siege" - auf 0,11.
- Bewertungsaktualisierung :
- delta=K cdot(S−PrBeta(ri,rj)) .
- r(neu)i=ri+ delta , r(neu)j=rj− delta .
Hinweis : weil Der Unterschied in den Bewertungen wirkt sich direkt auf die Gewinnwahrscheinlichkeit in einem Frame aus, und nicht im gesamten Spiel sollte ein niedrigerer optimaler Koeffizientenwert erwartet werden K : Teil des Wertes delta kommt von einer verstärkenden Wirkung PrBeta(ri,rj) .
Die Idee, das Ergebnis eines Spiels anhand der Gewinnwahrscheinlichkeit in einem Frame zu berechnen, ist nicht sehr neu. Auf dieser Autorenseite von François Labelle finden Sie eine Online-Berechnung der Wahrscheinlichkeit, das "Beste von" zu gewinnen N Ich war froh zu sehen, dass unsere Berechnungsergebnisse übereinstimmen. Ich konnte jedoch keine Quellen für die Einführung eines solchen Ansatzes für das Aktualisierungsverfahren für Elo-Bewertungen finden. Nach wie vor bin ich für Informationen zu diesem Thema sehr dankbar.
Ich konnte diesen Artikel und die Beschreibung des Elo-Systems nur auf dem Backgammon-Spieleserver (FIBS) finden. Es gibt auch ein russischsprachiges Analogon . Hierbei werden unterschiedliche Übereinstimmungsdauern berücksichtigt, indem die Bewertungsdifferenz mit der Quadratwurzel der Übereinstimmungsentfernung multipliziert wird. Es scheint jedoch keine theoretische Rechtfertigung zu haben.
Ein Experiment
Ein Experiment hat mehrere Ziele. Basierend auf den Ergebnissen von Snooker-Matches:
- Bestimmen Sie die besten Koeffizientenwerte K für beide Modelle.
- Untersuchung der Stabilität von Modellen im Hinblick auf die Genauigkeit der Vorhersagewahrscheinlichkeit.
- Untersuchung der Auswirkung der Verwendung von Einladungsturnieren auf die Bewertungen.
- Erstellen Sie für alle Profispieler eine faire Bewertungshistorie für die Saison 2017/18.
Daten
Code zur Generierung von Experimentdaten # "train", "validation" "test" split_cases <- function(n, props = c(0.5, 0.25, 0.25)) { breaks <- n * cumsum(head(props, -1)) / sum(props) id_vec <- findInterval(seq_len(n), breaks, left.open = TRUE) + 1 c("train", "validation", "test")[id_vec] } pro_players <- snooker_players %>% filter(status == "pro") # pro_matches_all <- snooker_matches %>% # filter(!walkover1, !walkover2) %>% # semi_join(y = pro_players, by = c(player1Id = "id")) %>% semi_join(y = pro_players, by = c(player2Id = "id")) %>% # 'season' left_join( y = snooker_events %>% select(id, season), by = c(eventId = "id") ) %>% # arrange(endDate) %>% # widecr transmute( game = seq_len(n()), player1 = player1Id, score1, player2 = player2Id, score2, matchId = id, endDate, eventId, season, # ("train", "validation" "test") # 50/25/25 matchType = split_cases(n()) ) %>% # widecr as_widecr() # (, # , Championship League). pro_matches_off <- pro_matches_all %>% anti_join( y = snooker_events %>% filter(type == "Invitational"), by = c(eventId = "id") ) # get_split <- . %>% count(matchType) %>% mutate(share = n / sum(n)) # 50/25/25 (train/validation/test) pro_matches_all %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 1030 0.250 ## 2 train 2059 0.5 ## 3 validation 1029 0.250 # , # . , # __ __, `pro_matches_all`. # , __ # __. pro_matches_off %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 820 0.225 ## 2 train 1810 0.497 ## 3 validation 1014 0.278 # K k_grid <- 1:100
Wir werden die Snooker-Daten aus dem Comperank- Paket verwenden. Die ursprüngliche Quelle ist snooker.org . Die Ergebnisse stammen aus folgenden Spielen:
- Das Spiel wurde in der Saison 2016/17 oder 2017/18 gespielt .
- Das Match ist Teil eines „professionellen“ Snookerturniers , das heißt:
- Es ist vom Typ "Einladung", "Qualifikation" oder "Rangliste". Wir werden auch zwei Sätze von Spielen unterscheiden: "alle Spiele" (von all diesen Turnieren) und "offizielle Spiele" (ausgenommen Einladungsturniere). Dafür gibt es zwei Gründe:
- Bei Einladungsturnieren haben nicht alle Spieler die Möglichkeit, ihre Bewertung zu ändern. Dies ist im Rahmen der Modelle Elo und EloBet nicht unbedingt schlecht, hat aber einen „Hauch von Ungerechtigkeit“.
- Es besteht die Überzeugung, dass die Spieler nur offizielle Bewertungsspiele „ernst nehmen“. Hinweis : Die meisten Einladungsturniere sind Teil der Championship League, die meiner Meinung nach von den meisten Spielern akzeptiert wird.
nicht sehr ernst in Form von Übung mit der Fähigkeit, Geld zu verdienen. Das Vorhandensein dieser Turniere kann sich auf die Rangliste auswirken. Neben der "Championship League" gibt es weitere Einladungsturniere: "China Championship 2016", beide "Champion of Champions", beide "Masters", "2017 Hong Kong Masters", "2017 World Games", "2017 Romanian Masters".
- Beschreibt einen traditionellen Snooker (nicht 6 Reds oder Power Snooker) zwischen einzelnen Spielern (keine Teams).
- Beide Geschlechter können beteiligt sein (nicht nur Männer oder Frauen).
- Spieler jeden Alters können teilnehmen (nicht nur Senioren oder "unter 21").
- Dies ist kein "Shoot-Out", weil Diese Turniere werden ansonsten in der Datenbank snooker.org gespeichert.
- Das Match hat wirklich stattgefunden : Das Ergebnis ist das Ergebnis eines echten Spiels, an dem beide Spieler beteiligt waren.
- Das Match findet zwischen zwei Profis statt . Die Liste der Profis wird für die Saison 2017/18 erstellt (131 Spieler). Diese Entscheidung scheint die umstrittenste zu sein die Entfernung von Spielen mit Amateur "Blinds" zur Niederlage von Profis von Amateur. Dies führt zu einem unfairen Vorteil dieser Spieler. Es scheint mir, dass eine solche Entscheidung notwendig ist, um die Ratinginflation zu reduzieren, die unter Berücksichtigung von Spielen mit Amateuren auftreten wird. Ein anderer Ansatz besteht darin, Profis und Amateure zusammen zu studieren. Dies erscheint jedoch im Rahmen dieser Studie unangemessen. Die Niederlage eines professionellen Amateurs gilt als Verlust der Möglichkeit, die Bewertung zu erhöhen.
Die endgültige Anzahl der verwendeten Spiele beträgt 4118 für "alle Spiele" und 3644 für "offizielle Spiele" (62,9 bzw. 55,6 pro Spieler).
Methodik
Experiment Funktionscode #' @param matches `longcr` `widecr` `matchType` #' ( : "train", "validation" "test"). #' @param test_type . #' #' ("") . , #' `game`. #' @param k_vec K . #' @param rate_fun_gen , K #' `add_iterative_ratings()`. #' @param get_win_prob #' (`rating1`, `rating2`) , #' (`frames_to_win`). ____: #' . #' @param initial_ratings #' `add_iterative_ratings()`. #' #' @details : #' - `matches` #' `game`. #' - `test_type`: #' - 1. #' - : 1 / #' (), 0.5 0 / (). #' - RMSE: , #' "" - . #' #' @return Tibble 'k' K 'goodness' #' RMSE. compute_goodness <- function(matches, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings = 0) { cat("\n") map_dfr(k_vec, function(cur_k) { # cat(cur_k, " ") matches %>% arrange(game) %>% add_iterative_ratings( rate_fun = rate_fun_gen(cur_k), initial_ratings = initial_ratings ) %>% left_join(y = matches %>% select(game, matchType), by = "game") %>% filter(matchType %in% test_type) %>% mutate( # framesToWin = pmax(score1, score2), # 1 `framesToWin` winProb = get_win_prob( rating1 = rating1Before, rating2 = rating2Before, frames_to_win = framesToWin ), result = get_match_result(score1, score2), squareError = (result - winProb)^2 ) %>% summarise(goodness = sqrt(mean(squareError))) }) %>% mutate(k = k_vec) %>% select(k, goodness) } #' `compute_goodness()` compute_goodness_wrap <- function(matches_name, test_type, k_vec, rate_fun_gen_name, win_prob_fun_name, initial_ratings = 0) { matches_tbl <- get(matches_name) rate_fun_gen <- get(rate_fun_gen_name) get_win_prob <- get(win_prob_fun_name) compute_goodness( matches_tbl, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings ) } #' #' #' @param test_type `test_type` ( ) #' `compute_goodness()`. #' @param rating_type ( ). #' @param data_type . #' @param k_vec,initial_ratings `compute_goodness()`. #' #' @details #' . #' , , #' : #' - "pro_matches_" + `< >` + `< >` . #' - `< >` + "_fun_gen" . #' - `< >` + "_win_prob" , #' . #' #' @return Tibble : #' - __testType__ <chr> : . #' - __ratingType__ <chr> : . #' - __dataType__ <chr> : . #' - __k__ <dbl/int> : K. #' - __goodness__ <dbl> : . do_experiment <- function(test_type = c("validation", "test"), rating_type = c("elo", "elobeta"), data_type = c("all", "off"), k_vec = k_grid, initial_ratings = 0) { crossing( testType = test_type, ratingType = rating_type, dataType = data_type ) %>% mutate( dataName = paste0("pro_matches_", testType, "_", dataType), kVec = rep(list(k_vec), n()), rateFunGenName = paste0(ratingType, "_fun_gen"), winProbFunName = paste0(ratingType, "_win_prob"), initialRatings = rep(list(initial_ratings), n()), experimentData = pmap( list(dataName, testType, kVec, rateFunGenName, winProbFunName, initialRatings), compute_goodness_wrap ) ) %>% unnest(experimentData) %>% select(testType, ratingType, dataType, k, goodness) }
"" K K=1,2,...,100 . , . :
- K ::
- . , .
add_iterative_ratings() comperank . " ", .. . - , ( ) , . RMSE ( ) ( ). , RMSE=√1|T|∑t∈T(St−Pt)2 wo T — , |T| — , St — , Pt — ( ). , " " .
- K RMSE . "" , RMSE K ( ). 0.5 ( "" 0.5) .
, : "train" (), "validation" () "test" (). , .. "train"/"validation" , "validation"/"test". 50/25/25 " ". " " " " . : 49.7/27.8/22.5. , , .
:
- : .
- : " " " " ( ". ").
- : "" ( "validation" RMSE "" "train" ) "" ( "test" RMSE "" "train" "validation" ).
Ergebnisse
pro_matches_validation_all <- pro_matches_all %>% filter(matchType != "test") pro_matches_validation_off <- pro_matches_off %>% filter(matchType != "test") pro_matches_test_all <- pro_matches_all pro_matches_test_off <- pro_matches_off
# experiment_tbl <- do_experiment()
plot_data <- experiment_tbl %>% unite(group, ratingType, dataType) %>% mutate( testType = recode( testType, validation = "", test = "" ), groupName = recode( group, elo_all = ", ", elo_off = ", . ", elobeta_all = ", ", elobeta_off = ", . " ), # groupName = factor(groupName, levels = unique(groupName)) ) compute_optimal_k <- . %>% group_by(testType, groupName) %>% slice(which.min(goodness)) %>% ungroup() compute_k_labels <- . %>% compute_optimal_k() %>% mutate(label = paste0("K = ", k)) %>% group_by(groupName) %>% # K , # . - # . mutate(hjust = - (k == max(k)) * 1.1 + 1.05) %>% ungroup() plot_experiment_results <- function(results_tbl) { ggplot(results_tbl) + geom_hline( yintercept = 0.5, colour = "#AA5555", size = 0.5, linetype = "dotted" ) + geom_line(aes(k, goodness, colour = testType)) + geom_vline( data = compute_optimal_k, mapping = aes(xintercept = k, colour = testType), linetype = "dashed", show.legend = FALSE ) + geom_text( data = compute_k_labels, mapping = aes(k, Inf, label = label, hjust = hjust), vjust = 1.2 ) + facet_wrap(~ groupName) + scale_colour_manual( values = c(`` = "#377EB8", `` = "#FF7F00"), guide = guide_legend(title = "", override.aes = list(size = 4)) ) + labs( x = " K", y = " (RMSE)", title = " ", subtitle = paste0( ' ( ) ', ' .\n', ' K ( ', '"") , .' ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_experiment_results(plot_data)
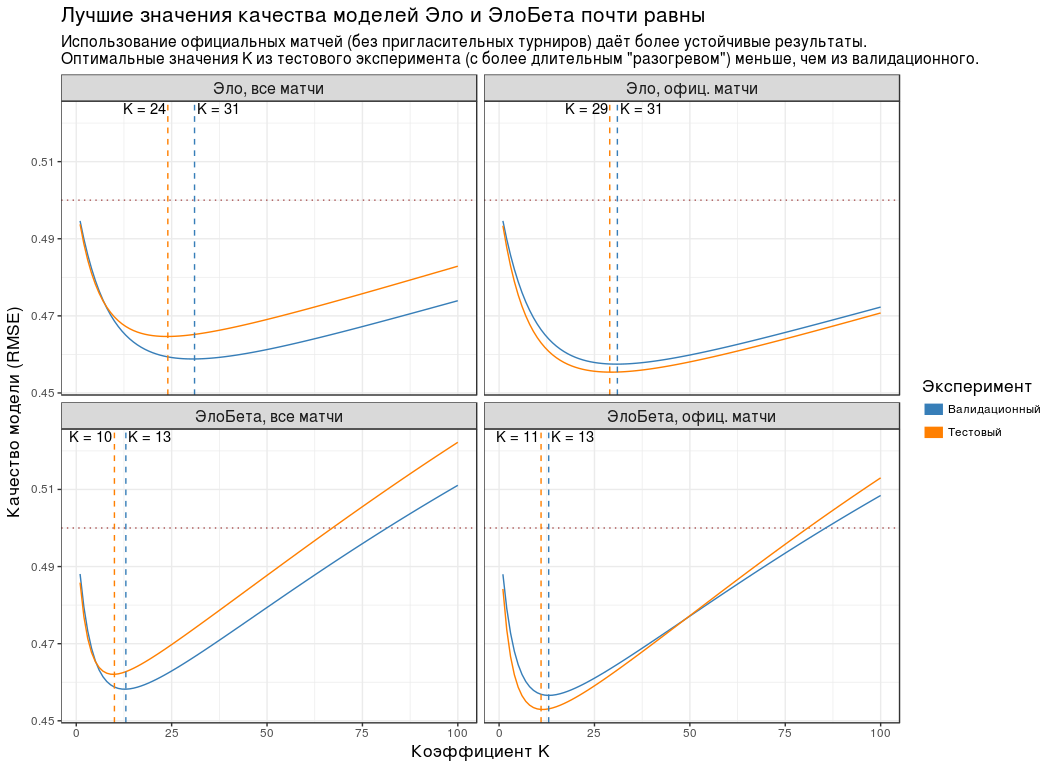
:
- , K , .
- ( "" "" ). , . - "Championship League": 3 .
- RMSE K . , RMSE K "" "". , " " .
- K ( "") , . "", .
- RMSE . 0.5. .
| Die Gruppe | K | RMSE |
|---|
| , | 24 | 0.465 |
| , . | 29 | 0.455 |
| , | 10 | 0.462 |
| , . | 11 | 0.453 |
Weil , K " " ( ) 5: 30, — 10.
, K=30 K=10 . , n , .
" " ( K=10 ) - .
-16 2017/18
-16 2017/18 # gather_to_longcr <- function(tbl) { bind_rows( tbl %>% select(-matches("2")) %>% rename_all(funs(gsub("1", "", .))), tbl %>% select(-matches("1")) %>% rename_all(funs(gsub("2", "", .))) ) %>% arrange(game) } # K best_k <- experiment_tbl %>% filter(testType == "test", ratingType == "elobeta", dataType == "off") %>% slice(which.min(goodness)) %>% pull(k) #!!! "" , .. !!! best_k <- round(best_k / 5) * 5 # elobeta_ratings <- rate_iterative( pro_matches_test_off, elobeta_fun_gen(best_k), initial_ratings = 0 ) %>% rename(ratingEloBeta = rating_iterative) %>% arrange(desc(ratingEloBeta)) %>% left_join( y = snooker_players %>% select(id, playerName = name), by = c(player = "id") ) %>% mutate(rankEloBeta = order(ratingEloBeta, decreasing = TRUE)) %>% select(player, playerName, ratingEloBeta, rankEloBeta) elobeta_top16 <- elobeta_ratings %>% filter(rankEloBeta <= 16) %>% mutate( rankChr = formatC(rankEloBeta, width = 2, format = "d", flag = "0"), ratingEloBeta = round(ratingEloBeta, 1) ) official_ratings <- tibble( player = c( 5, 1, 237, 17, 12, 16, 224, 30, 68, 154, 97, 39, 85, 2, 202, 1260 ), rankOff = c( 2, 3, 4, 1, 5, 7, 6, 13, 16, 10, 8, 9, 26, 17, 12, 23 ), ratingOff = c( 905750, 878750, 751525, 1315275, 660250, 543225, 590525, 324587, 303862, 356125, 453875, 416250, 180862, 291025, 332450, 215125 ) )
-16 2017/18 ( snooker.org):
| | | . | . Bewertung | |
|---|
| Ronnie O'Sullivan | 1 | 128.8 | 2 | 905 750 | 1 |
| Mark J Williams | 2 | 123.4 | 3 | 878 750 | 1 |
| John Higgins | 3 | 112.5 | 4 | 751 525 | 1 |
| Mark Selby | 4 | 102.4 | 1 | 1 315 275 | -3 |
| Judd Trump | 5 | 92.2 | 5 | 660 250 | 0 |
| Barry Hawkins | 6 | 83.1 | 7 | 543 225 | 1 |
| Ding Junhui | 7 | 82.8 | 6 | 590 525 | -1 |
| Stuart Bingham | 8 | 74.3 | 13 | 324 587 | 5 |
| Ryan Day | 9 | 71.9 | 16 | 303 862 | 7 |
| Neil Robertson | 10 | 70.6 | 10 | 356 125 | 0 |
| Shaun Murphy | 11 | 70.1 | 8 | 453 875 | -3 |
| Kyren Wilson | 12 | 70.1 | 9 | 416 250 | -3 |
| Jack Lisowski | 13 | 68.8 | 26 | 180 862 | 13 |
| Stephen Maguire | 14 | 63.7 | 17 | 291 025 | 3 |
| Mark Allen | 15 | 63.7 | 12 | 332 450 | -3 |
| Yan Bingtao | 16 | 61.6 | 23 | 215 125 | 7 |
:
- №1 3 . , , ( ).
- "" ( 13 ), ( 7 ).
- 5 . , 6 - WPBSA. , - "" . : , — .
- .
- ( №11), (№14) (№15) -16. "" (№26), (№23) (№17).
. , №16 (Yan Bingtao) №1 (Ronnie O'Sullivan) 0.404. 4 0.299, " 10 " — 0.197 18 — 0.125. , .
# seasons_break <- ISOdatetime(2017, 5, 2, 0, 0, 0, tz = "UTC") # elobeta_history <- pro_matches_test_off %>% add_iterative_ratings(elobeta_fun_gen(best_k), initial_ratings = 0) %>% gather_to_longcr() %>% left_join(y = pro_matches_test_off %>% select(game, endDate), by = "game") # plot_all_elobeta_history <- function(history_tbl) { history_tbl %>% mutate(isTop16 = player %in% elobeta_top16$player) %>% ggplot(aes(endDate, ratingAfter, group = player)) + geom_step(data = . %>% filter(!isTop16), colour = "#C2DF9A") + geom_step(data = . %>% filter(isTop16), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_vline( xintercept = seasons_break, linetype = "dotted", colour = "#E41A1C", size = 1 ) + geom_text( x = seasons_break, y = Inf, label = " 2016/17", colour = "#E41A1C", hjust = 1.05, vjust = 1.2 ) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = paste0( " -16 2016/17" ), subtitle = paste0( " ", " ." ) ) + theme(title = element_text(size = 13)) } plot_all_elobeta_history(elobeta_history)
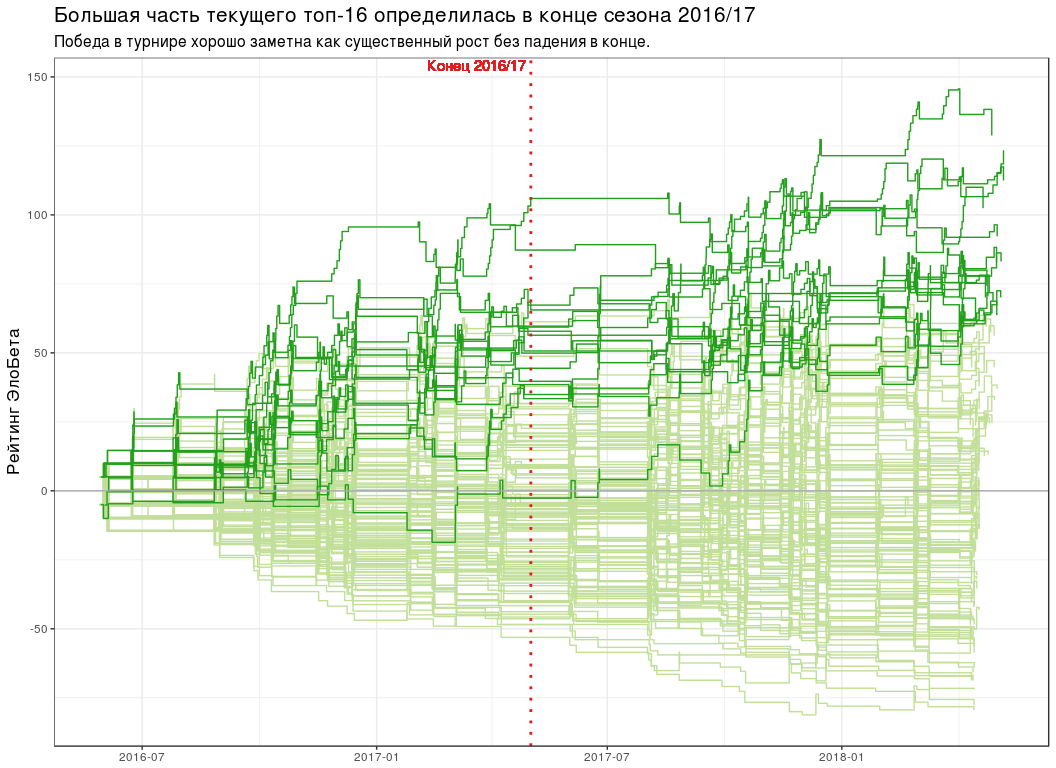
-16
-16 # top16_rating_evolution <- elobeta_history %>% # `inner_join` `elobeta_top16` inner_join(y = elobeta_top16 %>% select(-ratingEloBeta), by = "player") %>% # 2017/18 semi_join( y = pro_matches_test_off %>% filter(season == 2017), by = "game" ) %>% mutate(playerLabel = paste(rankChr, playerName)) # plot_top16_elobeta_history <- function(elobeta_history) { ggplot(elobeta_history) + geom_step(aes(endDate, ratingAfter, group = player), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_rug( data = elobeta_top16, mapping = aes(y = ratingEloBeta), sides = "r" ) + facet_wrap(~ playerLabel, nrow = 4, ncol = 4) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = " -16 ( 2017/18)", subtitle = paste0( " ' 2017/18.\n", " : 13- ." ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_top16_elobeta_history(top16_rating_evolution)
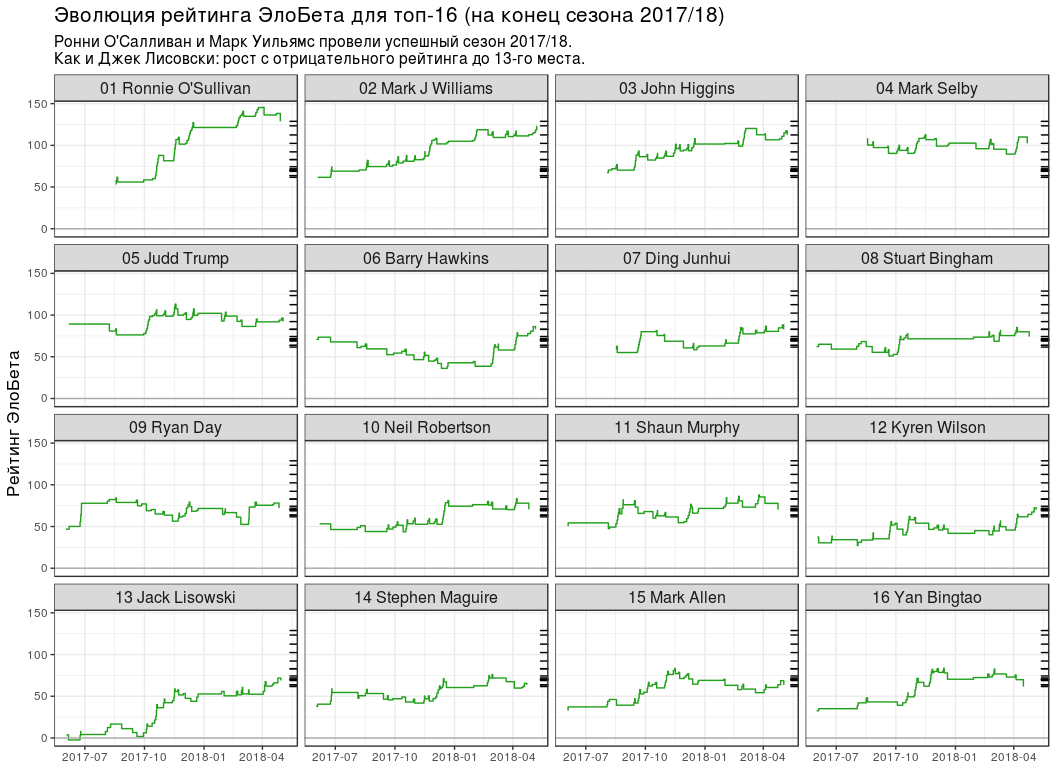
Schlussfolgerungen
- " " R :
pbeta(p, n, m) . - — "best of N " ( n ). .
- K=30 K=10 .
- :
sessionInfo() ## R version 3.4.4 (2018-03-15) ## Platform: x86_64-pc-linux-gnu (64-bit) ## Running under: Ubuntu 16.04.4 LTS ## ## Matrix products: default ## BLAS: /usr/lib/openblas-base/libblas.so.3 ## LAPACK: /usr/lib/libopenblasp-r0.2.18.so ## ## locale: ## [1] LC_CTYPE=ru_UA.UTF-8 LC_NUMERIC=C ## [3] LC_TIME=ru_UA.UTF-8 LC_COLLATE=ru_UA.UTF-8 ## [5] LC_MONETARY=ru_UA.UTF-8 LC_MESSAGES=ru_UA.UTF-8 ## [7] LC_PAPER=ru_UA.UTF-8 LC_NAME=C ## [9] LC_ADDRESS=C LC_TELEPHONE=C ## [11] LC_MEASUREMENT=ru_UA.UTF-8 LC_IDENTIFICATION=C ## ## attached base packages: ## [1] stats graphics grDevices utils datasets methods base ## ## other attached packages: ## [1] bindrcpp_0.2.2 comperank_0.1.0 comperes_0.2.0 ggplot2_2.2.1 ## [5] purrr_0.2.5 tidyr_0.8.1 dplyr_0.7.6 ## ## loaded via a namespace (and not attached): ## [1] Rcpp_0.12.17 knitr_1.20 bindr_0.1.1 magrittr_1.5 ## [5] munsell_0.5.0 tidyselect_0.2.4 colorspace_1.3-2 R6_2.2.2 ## [9] rlang_0.2.1 highr_0.7 plyr_1.8.4 stringr_1.3.1 ## [13] tools_3.4.4 grid_3.4.4 gtable_0.2.0 utf8_1.1.4 ## [17] cli_1.0.0 htmltools_0.3.6 lazyeval_0.2.1 yaml_2.1.19 ## [21] assertthat_0.2.0 rprojroot_1.3-2 digest_0.6.15 tibble_1.4.2 ## [25] crayon_1.3.4 glue_1.2.0 evaluate_0.10.1 rmarkdown_1.10 ## [29] labeling_0.3 stringi_1.2.3 compiler_3.4.4 pillar_1.2.3 ## [33] scales_0.5.0 backports_1.1.2 pkgconfig_2.0.1