Theorie des Glücks. Das Gesetz der Zebra- und Alien-Warteschlange

Ich mache die Leser von Habr weiterhin mit den Kapiteln aus seinem Buch "Theory of Happiness" mit dem Untertitel "Mathematical Foundations of the Laws of Meanness" bekannt. Dieses populärwissenschaftliche Buch ist noch nicht veröffentlicht und erzählt sehr informell, wie Mathematik es Ihnen ermöglicht, die Welt und das Leben der Menschen mit einem neuen Grad an Bewusstsein zu betrachten. Es ist für diejenigen, die sich für Wissenschaft interessieren und für diejenigen, die sich für das Leben interessieren. Und da unser Leben komplex und im Großen und Ganzen unvorhersehbar ist, liegt der Schwerpunkt des Buches hauptsächlich auf der Wahrscheinlichkeitstheorie und der mathematischen Statistik. Hier werden Theoreme nicht bewiesen und die Grundlagen der Wissenschaft nicht gegeben, dies ist keineswegs ein Lehrbuch, sondern das, was man Freizeitwissenschaft nennt. Aber genau diese fast spielerische Herangehensweise ermöglicht es uns, Intuition zu entwickeln, Vorlesungen für Studenten mit anschaulichen Beispielen aufzuhellen und schließlich Nicht-Mathematikern und unseren Kindern zu erklären, was wir in unserer trockenen Wissenschaft so interessant fanden.





Wir werden über Fatum, Erdbeben, Warteschlangen und wundervolle Prozesse sprechen: Poisson-Fluss, zufälliger Spaziergang und ein wenig über Markov-Ketten.

Zebra-Gesetz

Sie sagen, dass das Leben wie ein Zebra ist: entweder ein weißer oder ein schwarzer Streifen ... Und es kommt auch vor, dass ein anderer zu einem Problem hinzugefügt wird, und es ist so schwierig im Leben, und dann begann die Katze zu gebären! Es ist dick, es ist leer! Eins zu eins! Aber das Traurigste ist, dass, wenn ein heller Streifen gekommen ist und im Leben schlechte Gedanken auftauchen: Oh, ich würde es nicht verhexen, oh, wäre es nicht notwendig, für das Glück zu bezahlen ... Eine vertraute Sensation? Bei dieser Gelegenheit wird eines der Gesetze der Merphologie formuliert - das zweite Gesetz von Chisholm: " Wenn die Dinge gut laufen, sollte in naher Zukunft etwas passieren ." Da Francis Chisholm in seiner ursprünglichen Arbeit keine detaillierte Analyse oder Beweise für dieses Gesetz liefert, werden wir versuchen, selbst herauszufinden, ob eine Regelmäßigkeit dahinter steckt oder es uns nur so erscheint. Und wenn dies die Macken der Mathematik sind, ist es möglich, die charakteristische Dauer oder Häufigkeit der Streifen auf dem Körper unseres Zebras zu bestimmen, und wovon hängt es ab?

Im Leben passieren ständig Ereignisse. Manchmal sind sie überhaupt nicht miteinander verbunden, manchmal bilden sie Ketten von Ursache-Wirkungs-Beziehungen. Diskussionen über diese Verbindungen, Ketten und den vorgegebenen Lebensweg können uns sehr weit bringen, und wir werden später darüber sprechen. Versuchen wir in der Zwischenzeit wie immer, mit der geringsten Menge an Eingabedaten für die Analyse unseres Gesetzes auszukommen. Betrachten Sie eine Abfolge von Ereignissen, die nichts miteinander zu tun haben, und sehen Sie, was Sie daraus ziehen können.

Ereignisse, die in keiner Weise miteinander verbunden sind und zeitlich auftreten, werden mit dem bekannten Poisson-Stream zufällig beschrieben. Es entspricht vielen zufälligen Phänomenen von Erdbeben bis zum Auftreten von Kunden im Geschäft. Der Poisson-Strom von Ereignissen ist durch die Intensität oder Dichte des Stroms gekennzeichnet - ein Parameter, der die erwartete Anzahl von Ereignissen pro Zeiteinheit bestimmt. Zum Beispiel, wenn Sie die Zeit in Tagen messen, den Wert des Parameters $$$\ lambda = 1/7$Es wird durchschnittlich einmal pro Woche eine Kette von zufälligen Ereignissen geben. Dies bedeutet nicht, dass Ereignisse mit einer Häufigkeit von einmal pro Woche auftreten. Einer Folge von Ereignissen ist möglicherweise überhaupt keine Frequenz zugewiesen. Stellen Sie sich am besten einen Poisson-Stream mit einer Intensität von einmal pro Woche vor: 52 Wochen pro Jahr, was bedeutet, dass ungefähr 52 Ereignisse pro Jahr stattfinden sollten (im Durchschnitt über viele Jahre). Wenn wir 52 zufällige, gleichmäßig verteilte Daten in einem Jahr auswählen, können sie als Momente der Entstehung völlig unabhängiger Poisson-Ereignisse betrachtet werden.


Ein Beispiel für die Konstruktion eines Poisson-Stroms mit einer Intensität von 1/7 (Zeit wird in Tagen gemessen). Über einen Zeitraum von 365 Tagen wurden 52 Ereignisse, die nichts miteinander zu tun hatten, zufällig verteilt.

Darüber hinaus ist von keiner Periodizität dieser Ereignisse die Rede, wenn sie es wünschen, dann wird es passieren. Aber selbst in diesem Durcheinander können Statistiken uns bestimmte Muster zeigen. Beispielsweise ist die Verteilung der Dauer von Perioden zwischen den in der vorherigen Abbildung gezeigten Ereignissen überhaupt nicht einheitlich.


Die Dichte der Verteilung der Dauer von Lücken zwischen 52 Ereignissen, die zufällig über das 365-Tage-Intervall verteilt sind.

Die Verteilung der Dauer der Lücken ist tendenziell exponentiell , was durch eine durchgezogene Linie dargestellt wird. Für diese Verteilung liegt das Maximum (Modus) bei Null und der Durchschnittswert beträgt genau 7 Tage. Darüber hinaus beträgt die Standardabweichung ebenfalls 7 Tage. Die Gleichheit von Standardabweichung und Mittelwert ist eine charakteristische Eigenschaft der Exponentialverteilung. Wie Sie sehen können, garantieren diese Merkmale überhaupt nicht, dass eine Woche zwischen den Ereignissen vergeht, im Durchschnitt - ja, aber häufiger - weniger, außerdem können ziemlich lange Intervalle beobachtet werden. Schließlich zeigt der Median, dass die Hälfte aller Intervalle eine Dauer von nicht mehr als 5 Tagen haben wird. Intensität und Frequenz sind überhaupt nicht dasselbe, das ist ein sehr wichtiger Punkt!

Um fair zu sein, nehmen wir an, dass gute und schlechte Ereignisse gleich wahrscheinlich sind, aber helle und bedeutende Ereignisse viel seltener als kleine und unbedeutende. Es sei ein normales Leben, in dem die emotionale Färbung von Ereignissen der normalen (Gaußschen) Verteilung folgt. So könnte ein Jahr des synthetischen Schicksals als eine Reihe zufälliger, absolut unabhängiger Lebensveränderungen aussehen:

Eine Reihe von Ereignissen in verschiedenen emotionalen Farben, die einen Poisson-Strom mit einer Intensität von 2/7 bilden (2 Ereignisse in 7 Tagen).

Während keine Banden beobachtet werden, gibt es stattdessen etwas Rauschen. Jedes Ereignis verläuft spurlos und hinterlässt nichts in Erinnerung oder Stimmung. Es passiert nicht, lassen Sie uns unserem Modellhelden zunächst eine Erinnerung geben, ideal. Jedes Ereignis kann für immer in seiner Erinnerung bzw. in seiner Stimmung vergraben sein und es entweder verbessern oder verschlechtern. Hier ist ein Bild, das wir bekommen können, wenn wir zehn Jahre lang das Schicksal unseres Helden beobachten.

Ereignisse, die im Gedächtnis verschmelzen, bilden die emotionale Färbung des „synthetischen Lebens“.

Nun, wir sehen bereits eine Art Stimmungswechsel, aber das Bild kam nicht sehr freudig heraus. Unser Held fiel nach einer Reihe von Stimmungsschwankungen in eine tiefe Depression. Schade. Versuchen wir noch ein paar Schicksale. Alle von ihnen erleben eine Reihe von hellen und dunklen Streifen, aber für eine lange Zeit sind sie entweder in hoffnungsloser Sehnsucht oder in transzendentem Glück festgefahren. Das passiert natürlich, aber das ist eindeutig abnormal.

Einige Beispiele für „synthetische Schicksale“ von Menschen mit perfekten Erinnerungen.

Entspann dich, Alter!

Wir haben unser Modellschicksal als einen sehr bemerkenswerten Prozess beschrieben, der als eindimensionaler Zufallslauf bezeichnet wird und eine Reihe ungewöhnlicher Eigenschaften aufweist, unter denen Selbstähnlichkeit besteht, dh das Fehlen einer charakteristischen Zeitskala. Wenn Sie eine unbegrenzte Zeit zur Verfügung haben, kann ein zufälliger Spaziergang Sie unbegrenzt weit bringen, und außerdem führt er Sie mit Sicherheit zu einer vorgegebenen Entfernung über den Anfangswert! Egal wie gut Ihre Angelegenheiten sind, wenn sie zufällig wandern, werden sie sicherlich auf Null rutschen und nach unten gehen, es ist nur eine Frage der Zeit! Dieses berühmte und lehrreiche Gesetz des Lebens erhielt den Namensfluch des Spielers und sein Wesen kann durch eine einfache Maxime ausgedrückt werden:

Die beste Strategie beim Spielen ist es, ein Casino zu besitzen, sonst verlieren Sie.

Wir werden nicht auf dieses Ergebnis eingehen, das bereits sehr bekannt ist, aber wir werden immer noch auf diese Eigenschaft des eindimensionalen zufälligen Gehens stoßen.

Perfektes emotionales Gedächtnis scheint nicht sehr gut zu sein. Unsere Helden vergessen nichts und erinnern sich sorgfältig an alles, auch an die ältesten Ereignisse! Ihre Stimmung im Alter wird durch die Trauer über ein zerbrochenes Spielzeug in der Kindheit oder die Freude über einen Kuss in der Jugend beeinflusst. Darüber hinaus sind alle nachfolgenden Küsse und Spielzeuge für sie gleich wichtig. Es ist notwendig, diese armen Kerle zu retten. Emotionen lassen mit der Zeit nach, Trauer wird langweilig, Freude leider auch. Vergessen ist in vielerlei Hinsicht wie Abkühlen, Diffusion oder Verlangsamung einer Bewegung in einer viskosen Flüssigkeit. Es ist daher sinnvoll, sie auf diese Weise zu modellieren. Die aufgeführten Prozesse werden als Relaxationsprozesse bezeichnet . Geben wir unseren armen Mitmenschen die Möglichkeit, sich zu entspannen!

Das entspannende System kehrt in den Gleichgewichtszustand zurück und je schneller, desto größer ist die Abweichung vom Gleichgewicht. Diese Eigenschaft kann durch geometrische Progression oder Exponentialgesetz modelliert werden. Wir führen einen neuen Parameter in unser Modell ein - die Vergessensrate $$$\ mu$. Es kann in der Zeit ausgedrückt werden (in den Messwerten unseres Modells), in der der Grad der Emotion ziemlich stark abnimmt. Zum Beispiel für $$$\ mu = 1/60$Die emotionale Spur des Ereignisses wird in zwei Monaten um eine Größenordnung abnehmen. Und jetzt ist das Leben in einem guten "gestreiften" geworden!

Die Einschränkung des Gedächtnisses führt dazu, dass eine Reihe von Ereignissen und ihre Spuren im Gedächtnis eine Reihe emotional gefärbter Streifen bilden.

Wenn wir den "Grad der Vergesslichkeit" ändern, können wir mehr oder weniger emotional ausgeglichene Versuchspersonen erhalten. Es scheint, wir haben eine Quelle von Zebras gefunden! Dies sind zum einen zufällige Spaziergänge, die dazu neigen, sich in alle Richtungen auszubreiten, und zum anderen, um Vergesslichkeit zu heilen und die Stimmung wieder normal zu machen. Das Ergebnis ist eine wellenförmige Mäanderstimmung.

Lassen Sie uns die Eigenschaften der „synthetischen“ Weltstreifen untersuchen, die wir erhalten haben. Wir erstellen ein Histogramm, das die Verteilung ihrer Dauer für eine lange Lebensdauer (oder für viele gewöhnliche) mit Parametern zeigt $$$\ lambda = 1/7, \ quad \ mu = 1/60$.

Die Verteilung der Zeiträume von Glück und Trauer für eine große Anzahl synthetischer Schicksale. Die vertikale Linie markiert den Durchschnittswert von 33.

Das erste, was auffällt, ist die maximale Verteilung (Mode) nahe Null, was bedeutet, dass die Perioden des Glücks und des Unglücks meistens sehr kurz sind, es jedoch auch Perioden gibt, die länger als ein Jahr dauern. Im Durchschnitt beträgt die Dauer der Zeiträume 33 Tage mit einer Standardabweichung von 36 Tagen. Diese Verteilung ist nahezu exponentiell (tatsächlich wird sie durch eine allgemeinere Gammaverteilung mit Parametern beschrieben, die sie näher an die Exponentialverteilung bringen). Die exponentielle Verteilung der Längen der Bänder im Leben bedeutet wiederum, dass Stimmungsschwankungen als Poisson-Strom betrachtet werden können, dh als Kette unabhängiger zufälliger Ereignisse, die keine bestimmte Häufigkeit haben, aber mit einer bekannten Intensität auftreten. In dem von uns untersuchten Beispiel ändern sich beispielsweise dunkle und helle Streifen mit einer Intensität von einmal alle 33 Tage, gleichzeitig werden jedoch im Leben am häufigsten kurze Zeiträume beobachtet: Die Hälfte davon dauert nicht länger als zehn Tage.

In Abwesenheit von "Gedächtnis" (z $$$\ mu = 0$) nimmt die Verteilung nicht mehr exponentiell ab und wird exponentiell.

Die Verteilung der Mäanderdauern für einen zufälligen Spaziergang hat die Natur einer Kraftverteilung.

Statistiker sagen, dass solche Verteilungen einen schweren Schwanz haben , was sehr große Abweichungen vom Durchschnittswert sehr wahrscheinlich macht. Wir haben sie in Form von langen „Eintauchen“ in diese andere Stimmung beobachtet. Die von uns erhaltene Verteilung hat eine ungewöhnliche und seltsame Eigenschaft - weder der Mittelwert (Mittelwert) noch die Standardabweichung noch der Median sind dafür definiert. Tatsache ist, dass alle diese Eigenschaften basierend auf der Fläche unter der Verteilungsdichtekurve berechnet werden und unendlich sind. In dieser Hinsicht kann man hören, dass der Durchschnittswert in diesem Fall unendlich ist, aber dies ist nicht so. Sehen Sie, was passiert, wenn Sie versuchen, den Durchschnittswert der Mäanderdauer eines zufälligen Spaziergangs zu berechnen:

Der Versuch, den Durchschnittswert für eine Folge von Periodenlängen zwischen Stimmungsschwankungen ohne Gedächtnis zu berechnen. Aufkommende Extremwerte aus dem schweren Ende der Verteilung führen dazu, dass der Wert des Durchschnitts nicht gegen einen Wert konvergiert.

Riesige Sprünge, die vom schweren Schwanz ausgehen, senken den Durchschnittswert kontinuierlich und die Reihenfolge der Mittelung konvergiert nicht an eine Grenze. Der Mittelwert ist überhaupt nicht unendlich, nur das Integral konvergiert nicht gegen eine beliebige Zahl und es ist unmöglich, über einen bestimmten Wert zu sprechen. Es ist die Unmöglichkeit, den Mittelwert der Mäanderdauer zu berechnen, die die Selbstähnlichkeitseigenschaft von zufälligen Spaziergängen widerspiegelt, nämlich das Fehlen einer geeigneten Zeitskala.

Wir simulierten die Anpassungsfähigkeit an alltägliche Turbulenzen mithilfe von Entspannung oder Abschwächung emotionaler Ausbrüche. Dieser Prozess kann auf andere Weise interpretiert werden, als Anpassungsfähigkeit einer Person an die Lebensumstände. Bei der Verarbeitung von verrauschten Signalen oder Sequenzen wird häufig die Methode des gleitenden Durchschnitts verwendet, um ein nützliches Signal zu glätten und auszuwählen, wobei zu jedem Zeitpunkt nicht das Signal selbst, sondern der Durchschnittswert des Signals über einen bestimmten Zeitraum berücksichtigt wird. Auf diese Weise ist es möglich, Rauschen zu beseitigen und sich ein Bild von den langfristigen Trends des Signals zu machen. Wenn wir eine solche Mittelung auf alltägliche Turbulenzen anwenden, können wir die Anpassungsfähigkeit des Menschen simulieren. Und während Kriegen verlieben sich die Menschen und finden Grund zur Freude, so wie das Leben der reichen Faulenzer nicht wolkenlos ist. Die Norm verschiebt sich, von der die Stimmung in die eine oder andere Richtung abweicht. In Anbetracht des Unterschieds zwischen einer Folge von Emotionen und einer glatten Hintergrundlinie erhalten wir dasselbe Bild, Streifen, die uns das vorherige Modell mit denselben statistischen Merkmalen gegeben hat. Dies ist nicht überraschend, da sie sich konzeptionell praktisch nicht unterscheiden und ein System mit Entspannung beschreiben.

Mäanderförmige und sich ändernde Stimmungen können erhalten werden, indem der gleitende Durchschnitt der Anpassungsfähigkeit einer Person an die Umstände simuliert wird.

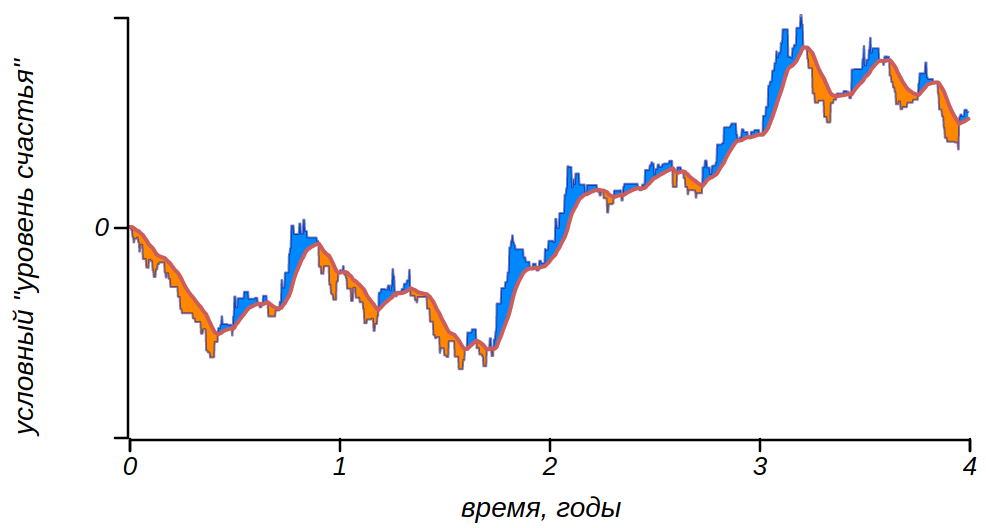
Verbunden durch eine Kette

In den betrachteten Modellen erhielten wir einen Poisson-Strom von Stimmungsschwankungen, der Ereignisse mit einem Poisson-Strom erzeugte. Darin ist eine gewisse Takelage zu erkennen - der Poisson-Zufallsprozess erwies sich als „in das Modell eingenäht“. Wie universell ist unser Ergebnis? Ist es möglich, es irgendwie anders zu bekommen?

Weltliche Erfahrung ist eine schlecht formalisierte Sache und kann an verschiedene mathematische Werkzeuge angepasst werden, um nicht nur Annahmen zu vereinfachen, sondern auch Spekulationen. In der Wissenschaft ist dieser Ansatz nicht akzeptabel, aber auf unserer Reise durch die Methoden der Theorie der Zufallsprozesse können wir es uns leisten, mit ihnen zu spielen, um sie besser kennenzulernen.

Wenn Sie die Dynamik der Stimmung und die Wahrnehmung der Welt beobachten, können Sie sehen, dass es die menschliche Natur ist, in einer bestimmten Stimmung zu „bleiben“. Wenn die Dinge insgesamt gut laufen, können die schlechten Nachrichten mit Optimismus aufgenommen werden. Und im Gegenteil, die melancholische Stimmung, die einmal von einer Person verschluckt wurde, kann sogar freudige Nachrichten verderben. Aus mathematischer Sicht bedeutet dies, dass die Wahrscheinlichkeit, in der aktuellen Stimmung zu bleiben, größer ist als die Wahrscheinlichkeit, sie zu ändern. Dieses Verhalten kann mithilfe eines zufälligen Prozesses beschrieben werden, der als Markov-Kette bezeichnet wird . Im allgemeinen Fall kann eine Markov-Kette als fester Satz von Zuständen mit Übergängen zwischen ihnen dargestellt werden, und Übergänge von Zustand zu Zustand haben eine andere, aber bekannte Wahrscheinlichkeit. Es ist zweckmäßig, solche Ketten in Form von gewichteten Graphen darzustellen. Beispielsweise kann eine elementare symmetrische Markov-Kette, die die Dynamik der Stimmung beschreibt, folgendermaßen dargestellt werden:


Markov-Kette mit zwei Zuständen ("freudig" und "traurig"). Die Pfeile geben die Übergänge und die Wahrscheinlichkeiten dieser Übergänge an. In unserem symmetrischen Fall übersteigt die Wahrscheinlichkeit, in einer bestehenden Stimmung zu bleiben, die Wahrscheinlichkeit ihrer Änderung, hängt jedoch nicht von der Stimmung selbst ab.

Unsere Kette ist in der Lage, Sequenzen von Zuständen zu erzeugen, und natürlich werden Banden weltlicher Zebras darin erscheinen.



Am interessantesten ist es herauszufinden, welche Distribution von der Dauer dieser Bands abhängt. Für unser mehr als einfaches Modell kann die Antwort genau sein - dies ist eine geometrische Verteilung , die die Wahrscheinlichkeit beschreibt, eine bestimmte Anzahl von Tests eines zufälligen Experiments zu beobachten, bevor der erste "Erfolg" beobachtet wird.

Ein Histogramm für die Dauer von Perioden gleicher Stimmung in der durch die symmetrische Markov-Kette erzeugten Sequenz und die Wahrscheinlichkeitsfunktion der geometrischen Verteilung mit einem Parameter, der der Wahrscheinlichkeit des Übergangs zwischen Zuständen entspricht. Die Sequenz ist zehn Jahre lang.

Eine geometrische Verteilung ist ein diskretes Analogon einer Exponentialverteilung in dem Sinne, dass die gerundeten Werte einer exponentiell verteilten Zufallsvariablen ihr gehorchen. Es besteht eine Beziehung zwischen dem geometrischen Verteilungsparameter und der Intensität der entsprechenden Exponentialverteilung. So erhalten wir wieder einen Poisson-Fluss von Stimmungsschwankungen, und für die von uns beschriebene Markov-Kette ist ihre Intensität $$$\lambda = -ln(0.75) \approx 2/7$.

Wenn wir die Symmetrie der Kette brechen, können wir einen „Optimisten“ oder einen „Pessimisten“ beschreiben, der eher bereit ist, in der einen oder anderen Stimmung zu „bleiben“. Die Verteilung der Streifendauern weicht von der Geometrie ab, gleichzeitig sind jedoch die meisten Streifen kurz. und jede hervorgehobene Periodizität wird nicht beobachtet.


Ein Histogramm für die Dauer von Perioden konstanter Stimmung in der von der asymmetrischen Markov-Kette erzeugten Sequenz. Die Sequenz ist zehn Jahre lang.

Markov-Ketten sind ein leistungsstarkes Werkzeug zur Analyse zufälliger Prozesse, in denen ein bestimmter Algorithmus oder ein bestimmtes Szenario liegt. Sie geben uns einen besonderen Blick auf die Prozesse, die als zyklisch gelten. Zum Beispiel wird die bekannte Maxime: „Die Geschichte der Menschheit wandelt sich im Kreis“ oft als die Tatsache interpretiert, dass es in der Geschichte bestimmte Zyklen oder sogar Periodizitäten gibt. Man muss zum Beispiel hören, dass der Beginn des Jahrhunderts Umwälzungen und Kriege verspricht. Ich gehe davon aus, dass es tatsächlich Sinn macht, nicht über wörtliche Zyklen zu sprechen, sondern über mehr oder weniger stabile Szenarien - reguläre Ketten, die von einer Markov-Kette beschrieben werden können. Unter den Markov-Ketten gibt es eine Klasse von cyclischen Ketten, die tatsächlich sich wiederholende Sequenzen erzeugen können.Es gibt jedoch keine echte deterministische Periodizität in ihrem Verhalten. Solche Zyklen treten zufällig in verschiedenen historischen Perioden und in verschiedenen Kontexten auf und sind einander ähnlich. Sie können ein Gefühl für historisches „Deja Vu“ erzeugen. Es ist nützlich, sie zu studieren und zu beschreiben, aber vielleicht sollten Sie keinen strengen Kalenderplan erwarten.

Darauf schließen wir das Thema Zebra. Welche Schlussfolgerungen können aus unserer leichtfertigen Forschung gezogen werden? Eine Reihe von hellen und dunklen Streifen im Leben ist keine Illusion, sie sind es wirklich. Aber es gibt keine besonderen Muster in ihnen. Meistens sind sie kurz, aber auch langwierig. Es hängt alles von der Leichtigkeit des Charakters und der Fähigkeit ab, die Vergangenheit loszulassen. Wenn Ereignisse im Leben selten vorkommen, wird das Leben zu einer grauen Reihe von Erinnerungen, die in der Vergangenheit verschwinden. Es liegt also in unserem Interesse, sich daran zu erinnern, was durchlebt wurde, und es liegt in unserer Macht, sicherzustellen, dass das Leben nicht zu einem zufälligen Gang wird. Wir können dafür sorgen, dass gute Ereignisse größer werden und häufiger stattfinden, auch wenn sie unbedeutend sind. Ein Skiausflug, ein aufrichtiges Lächeln eines Passanten, eine Konzertkarte, eine Tasse heiße Schokolade an einem kalten Tag,All dies wird dazu beitragen, einen positiven Trend zu erzeugen und den hellen Streifen im Leben zu verlängern. Der Durchschnittswert wird zwar dem Trend folgen, so dass unvermeidliche traurige Ereignisse zwangsläufig die Stimmung verändern. Aber beschuldigen Sie nicht Ihr Glück. Dies ist keine Vergeltung für ihn und nicht der böse Blick. Diese Eigenschaft entspannender Systeme ist eine Tendenz zu Schwingungen während der stochastischen äußeren Einwirkung.

Über das Warten auf einen Bus oder ein Erdbeben

Der Unterschied zwischen der Häufigkeit (Periode) und der Intensität des Ereignisflusses ist wichtig genug, um zu verstehen, wenn Sie Nachrichten hören oder die Ergebnisse wissenschaftlicher Forschung lesen. Zum Beispiel können Seismologen heute leider kein bestimmtes Erdbeben vorhersagen: seine Zeit, seinen Ort und seine Stärke. Die Methoden der langfristigen seismischen Vorhersage für einige Regionen wurden entwickelt, aber ihre Ergebnisse sind in der Sprache der Wahrscheinlichkeitstheorie formuliert, und was mit ihnen zu tun ist, ist nicht immer offensichtlich.

Für die Bucht von Avacha, an deren Ufern sich Petropawlowsk-Kamtschatski im Jahr 2018 befindet, wurde beispielsweise die folgende Prognose abgegeben : „Die Gesamtwahrscheinlichkeit von Erdbeben mit einer Stärke von mehr als 7,7, die in der Stadt Petropawlowsk-Kamtschatski eine Stärke von 7 bis 9 Punkten haben können, kann für den nächsten Fünfjahreszeitraum 52,3 erreichen. %. " Was bedeutet das?Morgen zittern? Und wann? Und wo? Leider sind wir noch nicht in der Lage, solche direkten Fragen zu beantworten. Die genaue Interpretation dieser Nachricht lautet wie folgt: Die Intensität des seismischen Flusses ist jetzt so, dass in den nächsten 500 Jahren ungefähr 52 Erdbeben auftreten werden (vorausgesetzt, der Fluss bleibt unverändert). Darüber hinaus kann sich die Prognose in einem Monat ändern. Die Intensität ähnelt in gewissem Sinne der augenblicklichen Bewegungsgeschwindigkeit: Um zu messen, dass Sie sich mit einer Geschwindigkeit von 60 km / h bewegen, ist es nicht erforderlich, alle 60 km eine ganze Stunde zu fahren. Und vor allem bedeutet die Prognose der Wissenschaftler nicht, dass zwischen den Erdbeben zehn Jahre vergehen, wie angenommen werden kann, und 500 Jahre in 52 Ereignisse aufteilen. Wenn es also zehn Jahre lang keine starken Erdbeben gegeben hat, bedeutet dies nicht, dass es heute oder morgen nicht passieren wird. Es wird natürlich passieren, aber wie viel wird es dauern, um zu warten,ist unbekannt.

Sehen Sie sich an, wie sich das Niveau der seismischen Aktivität in der Region Kamtschatka auf verschiedenen Zeitskalen ändert (Bild vom Standort des Seismic Activity Monitor des Zweigs Kamtschatka des Unified Geophysical Survey der Russischen Akademie der Wissenschaften).


Das niedrigere Aktivitätsniveau wird durch ein erhöhtes ersetzt. Die Aktivität „atmet“, jedoch nicht periodisch, sondern wie das gleiche zufällige Wandern mit Entspannung.

Erdbeben sind jedoch unangenehme Phänomene und lassen sie nicht länger auftreten. Es gibt Dinge, auf die Sie sich mit großer Ungeduld freuen, wie zum Beispiel einen Bus. Wenn wir an der Bushaltestelle ankommen, möchten wir natürlich sofort die gewünschte Bus- oder Straßenbahnlinie nehmen, aber höchstwahrscheinlich schlägt dies fehl. Wenn es dann an diesem Ort einen klaren Zeitplan gibt, schauen wir ihn uns an, dann auf die Uhr und tauchen dann in ein Buch oder Telefon ein. In der Mitte der Route wird jedoch häufig anstelle des Zeitplans das Verkehrsintervall angegeben, z. B. 15 Minuten. Dies bedeutet, dass wir bereits weit von der Bushaltestelle entfernt sind, mit der die Busse pünktlich abfahren, und dass sich ein Fehler ansammelt, der die Ankunft des Busses zufällig macht. Nun, 15, also 15, lass uns warten. Und hier müssen Sie bedenken, dass Sie im Durchschnitt genau 15 Minuten warten müssen, unabhängig davon, wann Sie kommen.Nun, wenn Busse von kamenBei einer Häufigkeit von 15 Minuten würde die durchschnittliche Wartezeit die Hälfte der Zeit betragen - 7,5 Minuten, aber mit Intensität wird es nicht funktionieren! In Ermangelung zusätzlicher Bedingungen wird die Transportbewegung durch einen Poisson-Strom modelliert, was bedeutet, dass die Wartezeit für den Bus dem Exponentialgesetz mit der gleichen Intensität folgt. Und die mathematische Erwartung für eine exponentiell verteilte Größe mit Intensität$$$\lambda$ gleich $$$1/\lambda$Somit ist unsere Schlussfolgerung erhalten. Und was völlig ärgerlich ist - wie viel Zeit Sie bereits an der Bushaltestelle verbracht haben, hat keinen Einfluss auf die Wahrscheinlichkeit, dass der Bus passt. Dies funktioniert als Eigenschaft der Exponentialverteilung wie der Mangel an Speicher , der mit der Unabhängigkeit von Poisson-Ereignissen verbunden ist.

Zusammenfassend. Wenn Sie an der Bushaltestelle ankommen, müssen Sie eine klare Entscheidung treffen: Warten oder gehen und über das Thema nachdenken: Warten Sie noch oder gehen Sie zu Fuß - verurteilen Sie sich einfach, um das Gesetz der Gemeinheit zu erfüllen. Wenn Sie bereits 17 Minuten gewartet, gespuckt und zu Fuß gegangen sind, werden Sie höchstwahrscheinlich von dem lang erwarteten Bus oder sogar von zwei überholt. Nun, und so dass das Warten auf den Bus zu einem langwierigen und hoffnungslosen Kampf mit dem Schicksal wurde, erinnern wir uns an den Fluch des Radfahrers aus dem vorherigen Kapitel verlängert effektiv die beobachtete Wartezeit.


Interessanterweise ist die Lorentz-Kurve für die Exponentialverteilung für alle Intensitäten gleich. Somit gilt die Aussage für alle Poisson-Prozesse: Die Hälfte der gesamten Beobachtungszeit tritt in 20% der Fälle auf, in denen sich dieses nächste Ereignis verzögert. Der Gini-Koeffizient für die Exponentialverteilung beträgt genau 1/2.

Alien drehen

Ich denke über die Gesetze der Gemeinheit nach, die am Flughafen anstehen, um Passagiere und Gepäck einzuchecken. Die Schlange ist lang, die Menschen sind anders und fallen mit all ihren Taschen, Kindern oder Käfigen auf. Ich höre ein Grunzen von hinten: „Wie immer sind wir langsam an der Reihe. Schau, schau, dieser Schnurrbart in einer Mütze stand uns ebenbürtig und jetzt da drüben ... Das ist das Gesetz der Gemeinheit! Ich bin immer langsam dran! “ Dieses Gesetz nennt man die Beobachtung von Ettore:

"Die nächste Zeile bewegt sich immer schneller."

Es gibt ein ganzes Feld der Steuerungstheorie und der Theorie zufälliger Prozesse, die sich mit der Dynamik von Warteschlangen befassen. Dies ist wichtig für die Gestaltung von Geschäften und Warteräumen, die optimale Verwaltung des Operationssaals in der Bank, die Tore zur Mautautobahn und die Dokumentenverwaltung. Der Ausgangspunkt für die Modellierung der Warteschlange ist derselbe Poisson-Stream, da ein Minimum an zusätzlichen Annahmen erforderlich ist. Somit nehmen die Bewegungen desjenigen, der in der Warteschlange steht, die Form einer monoton wachsenden Stufenlinie an, wobei dieselben Schritte in zufälligen Intervallen auftreten. Die Akkumulation von Daten auf diese Weise wird als Poisson-Prozess bezeichnet .

So können sich zwei lange Schlangen bewegen:

Verschieben von zwei benachbarten Warteschlangen als Poisson-Prozesse mit gleicher Intensität.

Der Unterschied zwischen zwei identischen Poisson-Prozessen, nämlich dass er von einer Person beobachtet wird, die sich im Schwanz langweilt, ist eine Art zufälliger Gang. Und wenn ja, dann sind wir bereit, einige Schlussfolgerungen zu ziehen. Erstens: Der Abstand zwischen Personen, die gleichzeitig in denselben Warteschlangen stehen, nimmt zu oder ab, und es bilden sich charakteristische Mäander mit einer sich ständig ändernden Dauer. Die zweite Schlussfolgerung: Aufgrund der Selbstähnlichkeit von zufälligen Spaziergängen sowohl für kurze als auch für lange Bursts haben Mäander eine Dauer, die mit der Zeit vergleichbar ist, in der sie anstehen, was bedeutet, dass sie wahrgenommen werden und Mäander Anlass zur Unzufriedenheit geben. Die dritte Schlussfolgerung: Es ist nicht im Voraus bekannt, welche Warteschlange schneller wird, da ein zufälliger Spaziergang gleichermaßen wahrscheinlich sowohl nach oben als auch nach unten geht. Und schließlich die vierte Schlussfolgerung: Die Warteschlangen bewegen sich ab und zu unabhängig voneinander und holen sich im Durchschnitt auf, sie bewegen sich auf die gleiche Weise, und die erwartete Differenz zwischen ihnen tendiert gegen Null, aber die Streuung um den Durchschnitt nimmt mit der Zeit zu (in dem von uns beschriebenen Fall der Wert Die Verzögerung einer Warteschlange von einer anderen unterliegt der Verteilung von Skellam . Es stellt sich heraus, oder mit einer kurzen Linie erraten oder nicht - keine gemeinen Dinge vom Bösewicht des Schicksals!

Aber die Gesetze der Gemeinheit würden nicht Gesetze genannt, wenn sie keine Universalität beanspruchen würden. Wenn wir nicht das Glück haben, in der Nachhinein zu sein, werden wir mehr Zeit damit verbringen und mehr Möglichkeiten haben, uns über das Schicksal zu beschweren! Und jetzt Aufmerksamkeit, gute Nachricht: In jedem ausgewählten Zeitintervall sind diejenigen, die das Glück haben, mehr in die schnelle Warteschlange zu kommen als unglückliche Menschen, weil die schnelle Warteschlange mehr Menschen vermissen kann! Aber leider wird dies niemanden trösten, der in der Schlange steht.

---

Der eingereichte Text wurde noch nicht veröffentlicht, was bedeutet, dass er sich ändern kann. Ich hoffe, dass Kommentare und Bemerkungen von Lesern von Habr ihm helfen werden, sich zum Besseren zu verändern.