Ich mache die Leser von Habr weiterhin mit den Kapiteln aus seinem Buch "Theory of Happiness" mit dem Untertitel "Mathematical Foundations of the Laws of Meanness" bekannt. Dieses populärwissenschaftliche Buch ist noch nicht veröffentlicht und erzählt sehr informell, wie Mathematik es Ihnen ermöglicht, die Welt und das Leben der Menschen mit einem neuen Grad an Bewusstsein zu betrachten. Es ist für diejenigen, die sich für Wissenschaft interessieren und für diejenigen, die sich für das Leben interessieren. Und da unser Leben komplex und im Großen und Ganzen unvorhersehbar ist, liegt der Schwerpunkt des Buches hauptsächlich auf der Wahrscheinlichkeitstheorie und der mathematischen Statistik. Hier werden Theoreme nicht bewiesen und die Grundlagen der Wissenschaft nicht gegeben, dies ist keineswegs ein Lehrbuch, sondern das, was man Freizeitwissenschaft nennt. Aber genau dieser fast spielerische Ansatz ermöglicht es uns, Intuition zu entwickeln, Vorlesungen für Studenten mit anschaulichen Beispielen aufzuhellen und schließlich Nicht-Mathematikern und unseren Kindern zu erklären, was wir in unserer trockenen Wissenschaft so interessant fanden.Dies ist eines der ersten Kapitel, in denen wir am Beispiel eines Radfahrers die Werkzeuge betrachten, die wir zur Messung der Ungerechtigkeit benötigen: die Lorenzkurve und den Gini-Index sowie den berüchtigten Pareto und den beeindruckenden Inspektor.
Gesetz ist Gesetz
In diesem Buch werden wir über verschiedene Probleme sprechen. Bekannt, erwartet und so vorhersehbar, dass sie den Status von Gesetzen erhielten. Viele von ihnen wurden bereits formuliert: Dies ist das Gesetz des fallenden Sandwichs und Murphys Gesetz: "
Wenn es Probleme geben kann, wird es passieren. " Und die Chisholm-Gesetze zum Thema: "
Wenn die Dinge gut laufen, sollte in naher Zukunft etwas passieren." "und Ettores Beobachtung:"
Die nächste Runde geht immer schneller. "Die meisten von ihnen sind ziemlich trivial, aber nach Muirs Gesetz:"
Wenn wir versuchen, eine Sache herauszuholen, stellt sich heraus, dass sie mit allem anderen zusammenhängt. "Wir werden versuchen, einen rationalen Kern dieser Gesetze zu finden aber nicht für um sie zu bekämpfen, aber zum Vergnügen. Und da wir in diesem Fall die Mathematik verwenden werden, wird das Vergnügen im Gegensatz zum Ergebnis selbst eigenartig und nützlich sein. Nun, wenn unsere Argumentation uns zu weit führt, können wir das Persig-Postulat übernehmen: „
Die Anzahl vernünftiger Hypothesen, die ein bestimmtes Phänomen erklären, ist unendlich. “ Am Ende wies Grossman unter Berufung auf Kh. L. Menkin richtig darauf hin, dass „
Komplex Probleme haben immer einfache, leicht verständliche und falsche Lösungen. "
Einige der Probleme, die uns passieren, sind natürlich und entschlossen, andere stochastisch und probabilistisch.
Wenn Sie zum Beispiel Ihr Gehalt um 10% gesenkt und dann entschuldigt und um 10% erhöht haben, haben Sie am Ende verloren, weil
x(1−0,1)(1+0,1)=x(1−0,01)<x.
Wenn das Gehalt zuerst erhöht und dann, ohne sich zu entschuldigen, um die gleichen 10% gesenkt wird, ist das Ergebnis das gleiche, da es keine Rolle spielt, in welcher Reihenfolge die Koeffizienten multipliziert werden sollen. Es ist sehr einfach, beleidigend, hat aber nichts mit Glück zu tun.
Ein weiteres Beispiel für deterministische Probleme ist die Magie, die mit Kopfhörern in unseren Taschen geschieht: Wir stecken die ordentlich gefalteten Kopfhörer in unsere Tasche, und nach einer halben Stunde geschieht dort ein Wunder, und wir ziehen ein wildes Bündel Drähte aus unserer Tasche. 2007 veröffentlichten zwei Wissenschaftler aus dem sonnigen und ruhigen San Diego einen seriösen wissenschaftlichen Artikel mit dem Titel
„Spontane Bildung von Knoten auf einem angeregten Faden“, in dem die Verschleierung von Kopfhörern in einer Tasche detailliert analysiert und modelliert wird. Die auf Knotentheorie, Wahrscheinlichkeitstheorie und physikalischen Experimenten basierenden Autoren zeigen überzeugend, dass sich die Kopfhörer bei der Standard-Wicklungsmethode nach nur wenigen Sekunden Schütteln wirklich verheddern müssen. Wir beobachten dies jedoch bereits, nur die abgeleitete Verschränkungsgeschwindigkeit ist hier unerwartet. Es ist durchaus möglich, mit diesem Ärgernis auf mathematische Weise umzugehen: Sie müssen die Art und Weise ändern, in der die Kopfhörer gefaltet sind - nicht mit Ringen, die dazu neigen, Knoten zu bilden, sondern mit einer Reihe von Schleifen in der entgegengesetzten Richtung, wie in der Abbildung gezeigt. Bei dieser Faltmethode zerstören sich die Schleifen gegenseitig und die Knoten werden nicht gebildet. Seit vielen Jahren falte ich die Kopfhörer auf diese Weise zusammen und fühle mich wie ein cooler Topologe. Jedes Mal freue ich mich wie ein Trick, wenn sie sich von einem unachtsamen Händeschütteln abwickeln.

Aber selbst unter stochastischen Gesetzen ist nicht jeder gleich interessant. Zum Beispiel das Gesetz von Buk:
"Sie finden die Schlüssel immer in Ihrer letzten Tasche." hat keine rationale Grundlage. Eine einfache Berechnung zeigt, dass sich letztere bei gleicher Wahrscheinlichkeit, die Schlüssel für alle Taschen zu finden, nicht von den anderen unterscheidet. Ist es so, dass Sie zufällig alle Taschen überprüfen und sie trotzdem und mehrmals untersuchen? In diesem Fall gilt die Wahrscheinlichkeitsfunktion für die Nummer der Tasche, in der die Schlüssel erscheinen
N Taschen werden durch
geometrische Verteilung beschrieben :
P(n)= frac1N left(1− frac1N right)n−1,
und die erwartete Taschenzahl wird gleich sein
N . Das heißt, in gewissem Sinne wird das Buchengesetz umgesetzt. Auf diese Weise suchen wir jedoch nach Schlüsseln, es sei denn, wir müssen wirklich dringend auf die Toilette, und dann ist dies bereits ein vollwertiges Gesetz der Gemeinheit.
Wir werden uns für Gesetze interessieren, die paradox und lehrreich sind, Gesetze, die wie böser Stein aussehen und aus einer Vielzahl von Optionen die nervigsten und unangenehmsten auswählen, entgegen der Intuition, dass diese Wahl nicht die wahrscheinlichste sein sollte.
Wenn lang, lang, lang, wenn lang auf dem Weg ...
Ich bin ein großer Fan des Amateurradfahrens. Was gibt es Schöneres, als am frühen Morgen in der Kälte die Strecke entlang zu rasen, einen leichten Hang hinunterzurollen ... dieses Gefühl lohnt sich, um endlose Anstiege oder den Widerstand gegen den Gegenwind zu überwinden! Es stimmt, manchmal scheint es mehr Auf- als Abfahrten zu geben, und der Wind strebt danach, entgegenzukommen, wo immer Sie sich wenden. In diesbezüglichen Büchern zur Merphologie wird
das Radfahrergesetz angegeben:
Egal wohin Sie gehen - es geht bergauf und gegen den Wind.
Ich lebe in Kamtschatka, in Petropawlowsk gibt es viele Rutschen, und durch die Stadt zu fahren, kann man nicht vermeiden. Ich sollte jedoch beruhigt sein von dem Gedanken, dass ich von zu Hause aus wieder nach Hause zurückkehre, was bedeutet, dass der gesamte Abstieg gleich dem gesamten Aufstieg sein sollte. Eine radiale Route wird besonders ehrlich sein. Stellen Sie sich eine 2 km lange Strecke vor, die aus einem symmetrischen Hügel besteht: einen Kilometer hoch, einen Kilometer runter. Ich kann mit einer Geschwindigkeit von 10 km / h lange genug bergauf fahren und beim Abstieg versuche ich, eine Geschwindigkeit von 40 km / h zu halten (ja, ich bin vorsichtig und fahre mit einem Helm). Dies bedeutet, dass ich viermal mehr Zeit für den Aufstieg als für den Abstieg aufwenden werde, und das allgemeine Bild sieht wie folgt aus: 4/5 der Reisezeit werden für einen milden Aufstieg und nur 1/5 für einen angenehmen Abstieg aufgewendet. Es stellt sich als Schande heraus - 80% der Gehzeit bestehen aus schwierigen Abschnitten des Weges! Wenn ich aus unserer hügeligen Stadt in Richtung Meer oder ins Avachi-Flusstal pumpe, gibt es fast keine Rutschen, aber ich habe immer noch Gegenwind und guten Wind oder Abschnitte mit einer schlechten Straße.
Schauen wir uns das Gesetz des Radfahrers aus der Wahrscheinlichkeitstheorie an. Wenn ich während meiner Radtour viele Selfies mache und sie dann bekomme, ohne aus einem gemischten Rudel zu schauen, zeigt mir ein bedeutender Teil der Bilder eine gebogene Figur in einem orangefarbenen Helm, die demütig bergauf oder gegen den Wind kriecht. Die Wahrscheinlichkeit, einen fliegenden und leuchtenden Radfahrer auf einem Bild aus einem Werbebild zu sehen, beträgt leider nur etwa 20%. Und was wird die Statistik sagen? Wenn wir eine große Menge von Radfahrern auf einer hügeligen Strecke herauslassen, ein wenig warten und ihre Dichte beobachten, werden wir sehen, wie sich die meisten Athleten in schwierigen Gegenden drängen, und die Wahrscheinlichkeit, ein ruhiges lächelndes Gesicht in der allgemeinen Masse zu finden, wird nicht so groß sein!
Das Ergebnis der Simulationsmodellierung der Bewegung des Radfahrerensembles auf einer hügeligen Strecke. Für jeden Bewegungsteilnehmer wird seine Kraft eingestellt, er bestimmt seine Höchstgeschwindigkeit sowohl beim Aufstieg als auch beim Abstieg (Luftwiderstand wird berücksichtigt). Es ist zu sehen, wie schnell sich der größte Teil des Ensembles nach Beginn des Satzes auf die Höhen konzentriert.Zeigen wir wie in der Schule in der Grafik die Abhängigkeit der Bewegung des Radfahrers von der Zeit, wenn er sich entlang eines symmetrischen dreieckigen Hügels bewegt. Wir machen einfach alles auf erwachsene Art und Weise, in unserem eigenen Maßstab: Wir werden die Entfernung nicht in Kilometern messen, sondern in Bruchteilen des allgemeinen Weges, wir werden dasselbe mit der Reisezeit tun. Die erste Hälfte des Weges (Segment
AB ) Der Radfahrer bewegte sich langsam und lange -
4/5 die ganze Zeit und das zweite (Segment
B c ) schnell überwunden - für
1 / 5 Zeit.
Zeitplan des Radfahrers in Teilen des Gesamtweges und der Zeit.Es gibt eine völlig universelle Methode, um die Ungerechtigkeit dieser Welt zu beurteilen, die von Ökonomen, Demografen, Ökologen oder Vermarktern angewendet wird - die
Lorentz-Kurve und den zugehörigen
Gini-Index . Für eine bekannte Verteilung von etwas Wertvollem, beispielsweise Geld, in einer bestimmten Bevölkerung ist es möglich, nach dem Sortieren der Mitglieder der Menge durch Erhöhen des Wohlstands zunächst eine kumulative Kurve zu erstellen, wobei die X-Achse auf die Bevölkerungsgröße und die Y-Achse auf ihr allgemeines Wohlbefinden normalisiert wird. Das Ergebnis ist eine Kurve mit dem Namen des amerikanischen Ökonomen Max Otto Lorenz. Als wir die Bewegung des Radfahrers aufgezeichnet haben, haben wir im Wesentlichen die Lorenzkurve aufgezeichnet, um die Geschwindigkeiten entlang der Strecken eines Pfades zu verteilen, der nur aus zwei Spalten besteht.
Verteilung der Radfahrergeschwindigkeit auf dem zurückgelegten Weg.Natürlich kann nicht jeder Bewegungsplan als Lorentz-Kurve wahrgenommen werden. Bevor Sie es bauen, müssen Sie die Fahrzeiten nach Geschwindigkeit sortieren und dann mit dem Bau fortfahren. Mit anderen Worten, Sie müssen zuerst ein Histogramm der Geschwindigkeiten erstellen und dann nacheinander die Beiträge aller Spalten des Histogramms hinzufügen, beginnend mit dem Beitrag kleiner Werte, bis zum größten. Das Ergebnis sollte überall eine konkave Kurve sein, die unterhalb der Diagonale liegt (
A c ) Diese Diagonale wird als
Gleichheitskurve bezeichnet . In unserem Fall entspricht sie einer konstanten (Durchschnitts-) Geschwindigkeit entlang des gesamten Pfades oder einem Histogramm mit einer einzelnen Spalte (deltaförmige Wahrscheinlichkeitsdichtefunktion). Und im wirtschaftlichen Sinne - die universelle Gleichheit der Wohlfahrt. Je mehr die Lorentz-Kurve von der Gleichheitskurve abweicht, desto weniger „fair“ kann die Verteilung betrachtet werden. Sobald wir die Gesetze der Gemeinheit und Ungerechtigkeit unserer Welt studieren, ist es ratsam, sowohl die Terminologie als auch die Werkzeuge zu verwenden, die zum Studium der Gerechtigkeit verwendet werden.
Die Fläche unter der Lorentz-Kurve für eine andere Verteilung als die deltaähnliche Verteilung ist kleiner als die Fläche unter der Gleichheitskurve. Ihr Unterschied kann als formales Merkmal für Ungleichheit oder „Ungerechtigkeit“ der Verteilung dienen. Diese Eigenschaft spiegelt sich im
Gini-Index wider. Sie wird als doppelte Fläche der Figur berechnet, die durch die Gleichheitskurve und die Lorentzkurve gebildet wird. Für eine ideale Welt ist der Gini-Index 0, in der albtraumhaftesten Version eher eins. In dem untersuchten Beispiel ist es 0,35. Dies ist ein ziemlich guter Indikator. Zum Beispiel hat die Verteilung des Wohlstands unter der Bevölkerung in Russland jetzt einen Gini-Index von 0,39, in den USA von 0,49, in Österreich und Schweden von nicht mehr als 0,3 und für die ganze Welt im Jahr 2017 von 0,66. Die Situation mit Radfahrern ist natürlich beleidigend und unfair, aber ziemlich tolerant.
Wir haben die Verteilung der Geschwindigkeiten nach Entfernung betrachtet und was passiert, wenn wir die Verteilung der Geschwindigkeiten nach Zeit erhalten (wir teilen die Fahrzeit in Intervalle auf und zählen die Anzahl der Intervalle mit der einen oder anderen Geschwindigkeit). Aufgrund der Dimensionslosigkeit des Lorentz-Diagramms können wir die entsprechende Kurve erneut zeichnen und sogar mit dem vorherigen Ergebnis vergleichen. Lassen Sie zum Beispiel die Hälfte der Reisezeit, beispielsweise eine Stunde, eine Radfahrerfahrt mit einer Geschwindigkeit von 10 km / h und eine Stunde mit einer Geschwindigkeit von 40 km / h (es spielt keine Rolle, in welcher Reihenfolge). Dann fällt 1/5 des gesamten Pfades auf eine niedrige Geschwindigkeit und 4/5 auf eine hohe Geschwindigkeit. Die Lorentz-Kurve ist im Fall einer Geschwindigkeitsverteilung über die Zeit eine Reflexion der Lorentz-Kurve für die Verteilung der Geschwindigkeiten über eine Entfernung relativ zur Diagonale senkrecht zur Gleichheitslinie. In diesem Fall ist der Gini-Index derselbe, da sich der Bereich darunter nicht ändert, wenn die Kurve reflektiert wird. Entsprechend dem Grad der Ungerechtigkeit erweisen sich diese beiden unterschiedlichen Zustände als gleich, obwohl der zweite Fall viel angenehmer zu sein scheint!

Bitte beachten Sie, dass wir mit Hilfe eines formalen Index begonnen haben, völlig unterschiedliche und unvergleichliche Dinge zu vergleichen. Dies ist sowohl verlockend als auch gefährlich. Sie müssen sich bewusst sein, dass formale Indizes und Kriterien immer gleich etwas sind, unabhängig davon, ob es sinnvoll ist oder nicht. Wir vergleichen die Verteilung des Wohlstands unter der Bevölkerung der Länder und die Verteilung der Zeit, die für die Überwindung des Pfades aufgewendet wurde, im Hinblick auf Unterschiede zu einigen Optionen, die als fair angesehen würden. Solange wir frivole und manchmal hooliganische Gespräche über die Gesetze der Gemeinheit führen, ist dies vielleicht ein gerechtfertigter Vergleich, aber in der Mathematik ist dies natürlich nicht möglich. Die Lorentz-Kurve und daraus der Gini-Index können formal für das Histogramm der Helligkeit der Pixel im Bild oder für die Häufigkeit der Wörter in der Live-Sprache berechnet werden. Dies hat keinen Bezug zur Gerechtigkeit, und es ist sehr wenig sinnvoll. Unter Berücksichtigung des Gini-Index für etwas Schreckliches werden wir ihn daher
den Gemeinheitsindex nennen, um den Leser nicht durch die Verrücktheit der Begriffe irrezuführen.
∗ ∗ ∗
Die Schlussfolgerung, die der Radfahrer keuchend in einem niedrigeren Gang zieht: „Die Welt ist unfair und der größte Teil der Energie nimmt den dümmsten Teil der Arbeit ein“, oft als
Pareto- Prinzip oder
„80/20“ -Prinzip bezeichnet . Dies ist absoluter Empirismus, niemand hat das Pareto-Prinzip bewiesen, aber es wird so oft zitiert, dass es bereits den Eindruck von Wahrheit erweckt. Es wird als Ausrede und als Anweisung verwendet, es findet sich in verschiedenen Erscheinungsformen und manchmal funktioniert es, zum Beispiel entspricht das Prinzip "80/20" dem Mittelwertindex in der Größenordnung von 0,6 - wie für die Verteilung des Reichtums auf der ganzen Welt. Wenn man versteht, dass dies nicht die Handlung des Schicksals ist, sondern die einfachste Mathematik, mit der es keinen Sinn macht, zu kämpfen, kann man lernen, sowohl die langwierigen Höhen als auch die mühsamen, aber unvermeidlichen Phasen der Arbeit zu genießen, zumindest Probleme im Kopf zu lösen oder zu meditieren. Taoisten bemühten sich, für immer zu leben, und argumentierten richtig, dass zusammen mit der Arbeit am Körper, um ihr Ziel zu erreichen, die Vorbereitung des Geistes erforderlich ist. In der Tat braucht man für das ewige Leben nicht nur die Fähigkeit, die Anhaftung loszulassen, sondern auch Geduld und die Fähigkeit, lange Strecken zu genießen.
Das Pareto-Prinzip hat eine strengere Verallgemeinerung, die zum Verständnis nützlich ist. Das Gesetz der Gemeinheit, benannt nach dem namenlosen Radfahrer, hat einen offiziellen wissenschaftlichen Titel: das
Paradox der Inspektion . Dieses bekannte Phänomen findet sich in einer Vielzahl von Studien im Zusammenhang mit soziologischen Untersuchungen, Tests in der Theorie der Fehler (ein Abschnitt der angewandten Mathematik, der sich mit der Zuverlässigkeit komplexer Systeme befasst), wobei die beobachteten Ergebnisse implizit, aber systematisch in Richtung häufiger beobachteter Phänomene verschoben werden.
Lassen Sie uns ein klassisches Beispiel mit einer Umfrage unter Fahrgästen des öffentlichen Verkehrs geben. Viele Busse verkehren täglich auf der Strecke, zu einer relativ kurzen Hauptverkehrszeit laufen die Busse über und der Rest der Zeit fahren sie fast leer. Wenn wir Passagiere befragen, wird ein erheblicher Teil von ihnen in einem überfüllten Bus sitzen (es sind einfach mehr Leute da), und wir werden Ausdruck allgemeiner Unzufriedenheit bekommen. Wenn wir die Fahrer befragen, werden sie sich über die Unvollständigkeit eines wesentlichen Teils der Strecken und die Unangemessenheit der Behörden beschweren, die sie vergeblich fahren. Ein flexibler Fahrplan wird die Situation glätten, aber in jedem Fall wird die Lorentz-Kurve von der Gleichheitskurve abweichen, die der unglaublichen Situation von immer der gleichen Anzahl von Fahrgästen in allen Bussen entspricht.
In Einführungen in die Wahrscheinlichkeitstheorie wird häufig eine spezielle undurchsichtige Tasche gefunden, in die Mathematiker verschiedene Objekte legen und sie dann zufällig herausziehen, wobei sie manchmal sehr nachdenkliche Schlussfolgerungen ziehen. Die Lösung für das Paradoxon besteht darin, dass wir das Passagierflusssystem als Ganzes analysieren und die Busse in die Tasche stecken. Bei der Durchführung der Umfrage nehmen wir die Passagiere nach dem Zufallsprinzip heraus (inspizieren) und versuchen, daraus Schlussfolgerungen zu ziehen. Das Bild zeigt den Unterschied:
Busstatistiken besagen, dass 75% von ihnen kostenlos und nutzlos sind. Gleichzeitig wird eine Passagierumfrage ergeben, dass 64% der an diesem Tag reisenden Passagiere in überfüllten Fahrzeugen waren.Schauen wir uns diese Situation an, indem wir die Lorenz-Kurve, diesmal die reale, für die Anzahl der Passagiere in den Bussen aus der vorherigen Abbildung zeichnen. Dazu müssen Sie die Busse nach der Anzahl der Fahrgäste sortieren und nacheinander den Beitrag jedes einzelnen zum gesamten Fahrgastfluss zusammenfassen:Die Lorenzkurve zeigt deutlich die beobachtete Ungerechtigkeit der Bussituation: Die Hälfte der Busse befördert nur ein Fünftel des Passagierstroms.Die Lorentz-Kurve zeigt in diesem Fall, wie sich die Quantile der Verteilung der Anzahl der Elemente in einigen Gruppen (horizontale Achse) verschieben, wenn die Verteilung der Elemente nach Gruppenzugehörigkeit (vertikale Achse) analysiert wird. Dies ist in der Tat das Paradox der Inspektion: Das Bild, das der Inspektor beobachtet, stellt sich als verzerrt heraus, da er nicht die Gruppen, sondern die Elemente der Gruppen analysiert, während der beobachtete Durchschnitt und der Median in Richtung eines „gewichtigeren Endes“ der Verteilung verschoben werden.An sich ist das Gesetz unseres Radfahrers sehr einfach, aber es wird die anderen Gesetze der Gemeinheit von Zeit zu Zeit verschärfen und ihnen einen mürrischen emotionalen Ton hinzufügen. Wenn ich über die Gesetze der Gemeinheit nachdenke, denke ich gerne über die Verzerrung der Wahrnehmung der Welt durch den Inspektor nach, indem ich die Farbkurven eines Bildes ändere. In Raster-Grafikeditoren verwenden wir das Kurven-Werkzeug, um Bilder zu ändern und die Verteilung der Pixelanzahl in der Helligkeit zu verschieben. Hier zum Beispiel, wie die Lorentz-Kurve, die wir für Busse erhalten haben, die Wahrnehmung der Realität verändert. Das Bild der Welt wird dunkler, wie wir erwarten.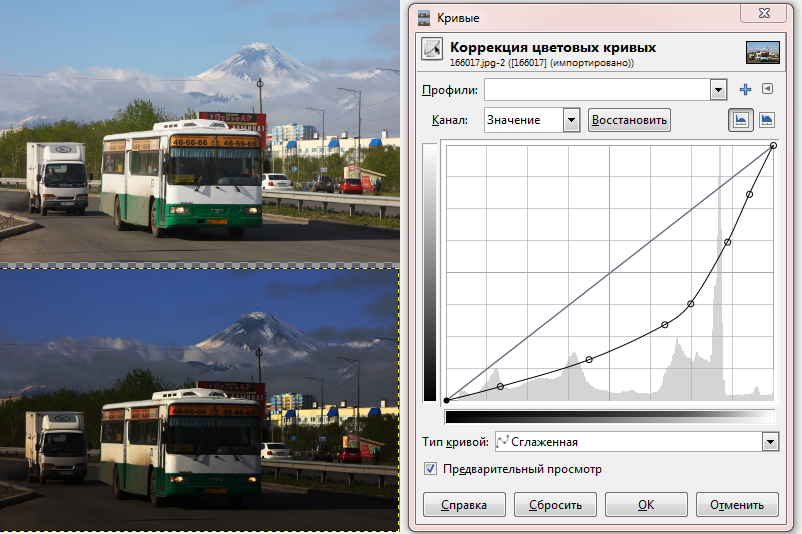
Die Erfahrung mit der Veröffentlichung von Kapiteln über Habré erwies sich als sehr nützlich: Durch die Kommentare der Leser konnte ich den Wortlaut korrigieren, die Beispiele erweitern und meinen eigenen Horizont erweitern. Ich werde mich freuen, im Buch selbst darüber zu sprechen, wie unsere Community bei der Bearbeitung geholfen hat, und den Machern und Bewohnern von Habr für die Teilnahme an seinem Schreiben zu danken.