Pythagoreische mathematische Begründung der musikalischen Skala

Ein Kapitel aus dem Buch von Alexander Woloschinow „Mathematik und Kunst“ (Moskau: Aufklärung, 1992)

Der ehrwürdige Pythagoras lehnte die Bewertung von Musik aufgrund von Gefühlsbeweisen ab. Er argumentierte, dass ihre Tugenden vom Verstand wahrgenommen werden sollten, und beurteilte die Musik daher nicht nach Gehör, sondern auf der Grundlage mathematischer Harmonie und fand es ausreichend, das Studium der Musik auf eine Oktave zu beschränken.

Plutarch

Genau genommen handelt es sich um das pythagoreische System. Was ist Gamma und Skala in der Musik?

Gamma oder Skala ist eine Folge von Klängen (Schritten) eines Musiksystems (Bund), die ausgehend vom Hauptklang (Hauptton) in aufsteigender oder absteigender Reihenfolge angeordnet sind. Der Name "Gamma" stammt vom griechischen Buchstaben Gγ (Gamma), der im Mittelalter den extrem tieferen Ton der Skala und dann die gesamte Skala bezeichnete.

Das wichtigste Merkmal eines musikalischen Klangs ist seine Tonhöhe , die sich im Bewusstsein der Schwingungsfrequenz eines klingenden Körpers wie einer Saite widerspiegelt. Je höher die Schwingungsfrequenz der Saite ist, desto höher erscheint uns der Klang.

Jeder einzelne Klang bildet kein Musiksystem und löst, wenn er nicht zu laut ist, nicht viel Reaktion aus. In anderen Fällen erweist sich jedoch bereits die Kombination zweier Klänge als angenehm und harmonisch, in anderen Fällen „schneidet“ sie im Gegenteil das Ohr. Eine vereinbarte Kombination zweier Töne wird als Konsonanz bezeichnet , eine inkonsistente Kombination als Dissonanz . Es ist klar, dass die Konsonanz oder Dissonanz zweier Töne durch den Höhenabstand zwischen diesen Tönen oder das Intervall bestimmt wird.

Das Intervall zwischen zwei Tönen ist die Seriennummer der Tonhöhe des oberen Tons relativ zum unteren in dieser Skala, und der Intervallkoeffizient I _{21 von} zwei Tönen ist das Verhältnis der Frequenz des oberen Tons zur Frequenz des unteren ^* :

(6.1)

^* ( In der Musiktheorie werden die Konzepte von Intervall und Intervallkoeffizient nicht streng unterschieden. Nach der Tradition wird der Intervallkoeffizient der Kürze halber häufig als Intervall bezeichnet. )

Betrachten wir nun einen bestimmten Satz von Klängen, indem wir beispielsweise mehrere Tasten eines Klaviers drücken. Höchstwahrscheinlich werden wir eine inkohärente Reihe von Geräuschen bekommen, wie sie sagen, weder das Lagerhaus noch den Bund. In anderen Fällen scheinen die Klänge zu passen und miteinander auszukommen, aber ihre Kombination wirkt zerlumpt und unvollendet. Ich möchte diese Sequenz bis zu einer bestimmten Note fortsetzen, die in diesem Klangsystem das stabilste, grundlegendste und als Tonikum bezeichnete zu sein scheint. Klänge in einem Musiksystem sind also durch bestimmte Abhängigkeiten miteinander verbunden, einige von ihnen sind instabil und ziehen andere an - stabil .

Aber nicht nur das Tonikum und die Kombination von stabilen und instabilen Klängen bestimmen die Natur des Musiksystems. Es ist einfach sicherzustellen, dass durch Drücken von acht weißen Tasten hintereinander von Note zu (Tonleiter zu Dur natürlich ) und von Note a ( natürliches Moll ) diese Tonleitern unterschiedlich klingen: Die erste - Dur - klingt fröhlich und leicht und die zweite - Moll - traurig und bewölkt ^* . Daher gibt es ein weiteres Merkmal des Soundsystems - die Stimmung: Dur oder Moll. So kommen wir zu einem der komplexesten Konzepte in der Musiktheorie - dem Konzept des Bunds.

^* (Die Art des Klangs des Bunds ist natürlich nicht so grob und eindeutig definiert. Diese Frage ist sehr heikel und wir werden am Ende des Kapitels darüber sprechen. )

Ein Bund ist ein für das Gehör angenehmes Zusammenspiel von musikalischen Klängen, das durch die Abhängigkeit instabiler Klänge von stabilen Klängen und vor allem von der stabilen Hauptsoundtonik und einer bestimmten klingenden Charakterneigung bestimmt wird. Die Geschichte der Musikkultur kennt viele Modi, die für verschiedene Völker und verschiedene Zeiten charakteristisch sind. Die alten Griechen kannten ungefähr ein Dutzend Bünde, und die Bünde einiger östlicher Länder und Indiens sind äußerst komplex, eigenartig und ungewöhnlich für das europäische Hören. Die gebräuchlichsten modernen Modi bestehen aus sieben Hauptschritten, von denen jeder erhöht oder verringert werden kann, wodurch fünf weitere zusätzliche Klänge erzeugt werden. Somit wird der diatonische (7-stufige) Gammabund chromatisch (12-Ton). Der erste Schritt des Bunds ist das Tonikum. Die Gesetze der Struktur des Bunds sind eine ganze Wissenschaft, der Eckpfeiler der Musikwissenschaft, und viele Wissenschaftler und Komponisten haben ihr ganzes Leben dem Studium dieser Gesetze gewidmet.

Wir werden uns hauptsächlich für die mathematischen Gesetze interessieren, die die Struktur des Bunds beschreiben, d. H. Das Musiksystem. Das Musiksystem ist der mathematische Ausdruck eines bestimmten Systems von Tonhöhenbeziehungen. Neben dem rein theoretischen Interesse findet das System Anwendung bei der Stimmung von Musikinstrumenten mit einer festen Tonhöhe, wie z. B. einem Klavier oder einer Orgel.

Zusammenfassend stellen wir fest, dass unsere Experimente mit dem Drücken der Tasten am Klavier mit dem seltensten und angenehmsten Phänomen enden können, wenn das aufgenommene Soundsystem nicht nur zu einem Bund gehört, sondern auch von Bedeutung ist. Eine solche künstlerisch bedeutsame sequentielle Reihe von Klängen unterschiedlicher Höhe wird als Melodie bezeichnet . Dies ist genau das, was wir je nach Stimmung gerne summen - peppig, traurig, fröhlich ...

Nach einem so kurzen Ausflug in die theoretische Musikwissenschaft können wir während der Zeit des weisen Pythagoras an die Ufer des sonnigen Hellas zurückkehren. Wir werden versuchen, die Argumentation von Pythagoras und seinen Schülern beim Aufbau des pythagoreischen Systems wiederherzustellen, da dieses System über Jahrtausende, wenn nicht für immer, die gesamte Entwicklung der Musikkultur bestimmte, nicht nur die europäische, sondern auch die östliche. Pythagoras selbst hat keine schriftlichen Werke hinterlassen, und das Erbe der Pythagoräer scheint ein hoffnungsloser Ruinenhaufen zu sein, d. H. Eine Sammlung versehentlich erhaltener Fragmente und späterer Zitate. Zweifellos sind diese Ruinen wunderschön und verblüffen immer noch die Fantasie, wie die Ruinen des berühmten Parthenon, aber viele dieser Fragmente sind vollständig verloren und man kann oft nur über das Ganze raten. Und doch ...

Monochord - einsaitig - war eines der ersten Musikinstrumente der alten Griechen. Es war eine lange Box, die benötigt wurde, um den Klang zu verstärken, über den die Saite gezogen wurde. Von unten wurde die Saite von einem mobilen Ständer gezogen, um die Saite in zwei getrennt klingende Teile zu teilen. Auf einer Holzkiste unter der Saite befand sich eine Teilungsskala, mit der genau bestimmt werden konnte, welcher Teil der Saite klingt. Natürlich wird uns das Monochord als Musikinstrument zu primitiv erscheinen, aber es war ein ausgezeichnetes physisches Instrument und ein Lehrmittel, mit dem alte Betrachter die Weisheit der Musikkompetenz verstanden haben.

Die Alten behaupteten, dass Pythagoras die Schwingungsgesetze der Monochord-Saite und die Konstruktion musikalischer Konsonanzen (Konsonanzen) bereits kannte. Wir finden jedoch eine Aufzeichnung dieser Gesetze vom pythagoreischen Architekten von Tarent (428-365 v. Chr.), Der anderthalb Jahrhunderte später als Pythagoras lebte . Der Architekt war natürlich der prominenteste Vertreter der pythagoreischen Schule, ein Freund des Philosophen Platon und ein Lehrer des Mathematikers Eudoxus (ca. 408 - ca. 355 v. Chr.), Ein Staatsmann und Kommandeur. Die Vielseitigkeit von Architus ist erstaunlich: Er löste das berühmte De-Los-Problem der Verdoppelung des Würfels, galt zu Recht als der größte pythagoreische Musiktheoretiker, der als erster die auf Mathematik basierende Mechanik rationalisierte und die Bewegungen von Mechanismen auf geometrische Zeichnungen reduzierte und an einem Holzmodell einer fliegenden Taube arbeitete. Nach Van der Waerden ist Arch der Autor des VIII. Buches "Die Anfänge" von Euklid, in dem die arithmetische Proportionstheorie dargelegt wird. Als Staatsmann war Archit äußerst respektiert: Er wurde sieben Jahre hintereinander ^* zum Strategen gewählt ^* , obwohl Strategen gesetzlich nur für ein Jahr ausgewählt wurden. Durch geschickte diplomatische Manöver rettete der Archit Platon aus der Gefangenschaft und rettete damit das Leben des großen Philosophen. "Herrliche Architekten, Land und Meer und Sandrechner ..." - schrieb Horace.

* ( Stratege - in den antiken griechischen Stadtstaaten ein Militärführer, der mit militärischen und politischen Schi-Ki-Kräften ausgestattet ist. )

Die "Gesetze des Pythagoras-Architekten", auf denen die gesamte pythagoreische Musiktheorie basiert, können wie folgt formuliert werden:

1- Die Tonhöhe (Schwingungsfrequenz f) der klingenden Saite ist umgekehrt proportional zu ihrer Länge l:

(6.2)

Hier ist a der Proportionalitätskoeffizient in Abhängigkeit von den physikalischen Eigenschaften der Saite (Dicke, Material usw.).

2. Zwei klingende Saiten geben nur dann Konsonanz, wenn ihre Längen als ganze Zahlen bezeichnet werden, die die Dreieckszahl 10 = 1 + 2 + 3 + 4 bilden, dh als 1: 2, 2: 3, 3: 4.

Diese Intervalle sind „perfekte Konsonanzen“, und ihre Intervallkoeffizienten erhielten später die lateinischen Namen ^* :

^* ( Die Namen der Intervalle in der Musik sind lateinische Ziffern, die die Seriennummer der Skala der Skala angeben, aus der das Intervall mit der Anfangsstufe besteht: Oktave - Achtel, Fünftel - Fünftel, Viertel - Viertel usw. )

Oktave

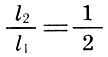
Quint

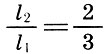
Quart

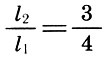
Dreieckszahl 10

Es wurde auch angemerkt, dass die vollständigste Verschmelzung von Tönen durch eine Oktave (2/1) gegeben ist, gefolgt von einem Quint (3/2) und einem Quart (4/3), d. H. Je kleiner die Zahl n in Bezug auf die Form ist 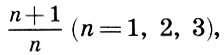Je konsonanter das Intervall.

"Das zweite Gesetz von Pythagoras - Architekt" und scheint jetzt überraschend. Was können wir über die Pythagoreer sagen, die er einfach begeistert hat? Hier fanden sie eine Bestätigung ihrer gesamten Philosophie: Ganzzahlen, außerdem regieren Tetraktis-Zahlen alles, sogar Musik! Die Pythagoräer ließen sich nicht lange warten und erweiterten das Gesetz der musikalischen Beziehungen, wo immer dies möglich war, einschließlich der Struktur des Universums.

Wenn wir also das Segment l gleich 1/12 der Länge der Monochord-Saite l ₁ als Preis für die Teilung der Monochord-Skala nehmen, dann sind zusammen mit der gesamten Monochord-Saite der Länge l ₁ = 12l ihre Teile der Länge l ₂ = 6l konsonant - der Klang ist eine Oktave höher (l ₂ / l ₁ = l / 2), l ₃ = 9l - ein Quint höher klingen (l ₃ / l ₁ = 2/3) und l ₄ = 8l - ein Quart höher klingen (l ₄ / l ₁ = 3/4) ) Diese Konsonanz und ihre definierenden Zahlen 6, 8, 9, 12 wurden Tetrade (vier) genannt. Die Pythagoräer glaubten, die Tetrade sei "die Skala, nach der Sirenen singen". Bei der Stimmung der alten Leier, die zum Symbol der Musik wurde, wurden ihre vier Saiten notwendigerweise nach der Regel der Tetrade gestimmt, und die Stimmung der verbleibenden Saiten hing vom Bund ab, in dem sie gespielt werden sollte.

Für den alten Denker reichte es jedoch nicht aus, die Zahlenwerte der untersuchten Größen zu ermitteln. Das pythagoreische Auge und der pythagoreische Geist sind es gewohnt, nicht nur zu messen, sondern auch zu messen, dh die inneren Verbindungen zwischen den untersuchten Probanden aufzudecken, mit anderen Worten, proportionale Beziehungen herzustellen. Der Architekt war ein wahrer Pythagoräer, und er stellte proportionale Beziehungen zwischen der perfekten Hauptkonsonanz her - einer Oktave, einer fünften und einer vierten. Diese Entscheidung wurde von Architekten im Zusammenhang mit dem Wunsch getroffen, die Oktave in harmonische Intervalle zu unterteilen. Wahrscheinlich ging Architus von der intuitiv offensichtlichen Annahme aus, dass zusammen mit den Tönen f ₁ und f ₂ = 2f ₁ die Hauptkonsonanz - eine Oktave - die Konsonanz und ihr arithmetisches Mittel f ₃ = (f ₁ + f ₂ ) / 2 ergeben sollte. Aber dann wird die Saitenlänge l ₃ in Form der Saitenlängen l ₁ und l ₂ gemäß (6.2) wie folgt ausgedrückt:

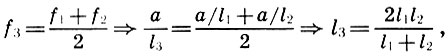
d.h. l ₃ ist das harmonische Mittel l ₁ und l ₂ (siehe 5.1). Das Gegenteil ist ebenfalls leicht zu erkennen: Das harmonische Mittel für die Frequenzen f ₁ und f ₂ geht in das arithmetische Mittel für die Längen l ₁ und l _{2 über} :

Daran erinnern 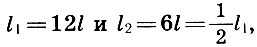Zusammen mit Architekten kommen wir zu einem wichtigen Ergebnis:

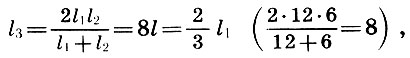
(6.3)


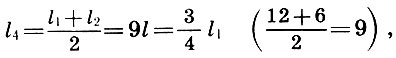
(6.4)

das fünfte ist das harmonische Mittel der Längen der Saiten des Grundtons l ₁ und der Oktaven l ₂ , und das Quart ist das arithmetische Mittel von l ₁ und l ₂ .

Das Produkt aus arithmetischem Mittel und harmonischem Mittel ist jedoch gleich dem Produkt der ursprünglichen Zahlen:

(6.5)

Wenn wir beide Teile durch l ₁ ² teilen, erhalten wir die zweite wichtige Schlussfolgerung:

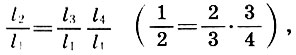
(6.6)

oder

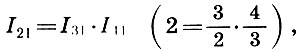
Das heißt, eine Oktave ist das Produkt eines Fünftels bis eines Viertels.

Durch Teilen von (6.5) durch l ₁ l ₃ erhält Archite den dritten der Hauptproportionen - geometrisch:

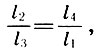
(6.7)

was "musikalisch" genannt wurde: Eine Oktave bezieht sich auf ein Quint ebenso wie ein Quart auf einen Grundton .

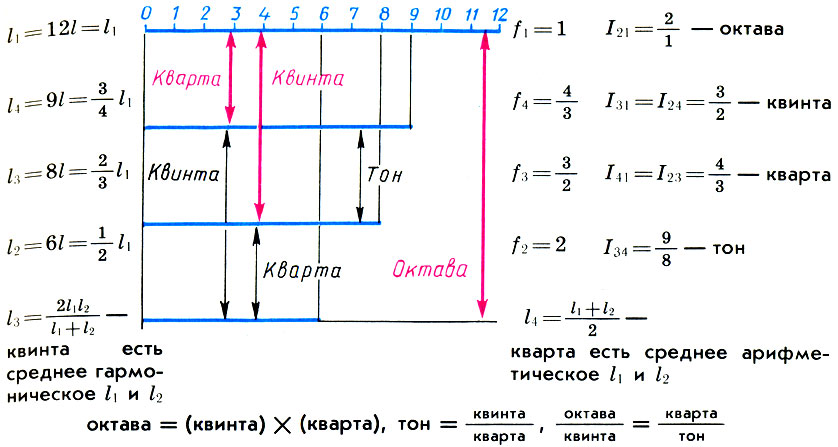
Aufteilung einer Monochord-Saite (l ₁ ) in Teile, die damit perfekte Konsonanzen bilden: eine Oktave (l ₂ ), eine fünfte (l ₃ ) und ein Quart (l ₄ ) und die Beziehungen zwischen ihnen. Die Intervalle, die eine ganze Monochordkette mit ihren Teilen bildet, sind durch rote Pfeile dargestellt

Es ist leicht, zwei weitere Beziehungen zu erhalten:

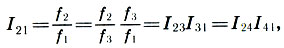
(6.8)

d.h. die Oktave ist in zwei ungleiche Konsonantenintervalle unterteilt - das fünfte und das vierte . Ein Intervall, das dieses Intervall auf eine Oktave erweitert, wird als Inversion bezeichnet . Das Quint ist also die Umkehrung des Quartetts und umgekehrt.

Schließlich finden wir den Intervallkoeffizienten zwischen den Saiten der Quinte l ₃ und des Quarz l ₄ , der zusammen mit seinem Intervall als Ton bezeichnet wird (verwechseln Sie nicht das Tonintervall und den Ton einer bestimmten Höhe):

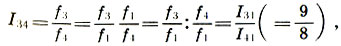
(6.9)

das Tonintervall ist gleich dem Verhältnis des fünften zum vierten .

Es ist zu beachten, dass im Gegensatz zu dem üblichen Abstand auf der Geraden r ₂₁ = x ₂ - x ₁ , der als Differenz zwischen den Koordinaten des Endes und des Anfangs definiert ist, der Intervallkoeffizient - der Höhenabstand - als das Verhältnis seiner konstituierenden Töne definiert ist 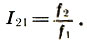Dann befinden sich drei Töne f ₁ <f ₂ <f _{3, die} sich in gleichen Abständen r befinden und eine arithmetische Folge x ₁ , x ₂ = x ₁ + r, x ₃ = x ₁ + 2r bilden. Daher werden die Intervallkoeffizienten "geometrisch" addiert und subtrahiert, und die Intervalle selbst - "arithmetisch", wie übliche Abstände, nämlich:

Die Summe zweier Intervalle entspricht dem Produkt ihrer Intervallkoeffizienten:

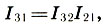
(6.10)

Die Differenz zweier Intervalle ist gleich dem Quotienten ihrer Intervallkoeffizienten:

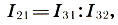
(6.11)

Das Teilen des Intervalls in n gleiche Teile bedeutet das Extrahieren einer Wurzel des Grades n aus ihrem Intervallkoeffizienten:

(6.12)

usw.

Um von Intervallkoeffizienten zu Abstandsintervallen zu gelangen, reicht es aus, das logarithmische Intervall L = log _a I und die logarithmische Frequenz F = log _a f einzuführen. Dann erhalten wir, Logarithmus der Definition (6.1) und Gleichheiten (6.10) - (6.12) die übliche Definition und Aktionsregeln mit Entfernungen:

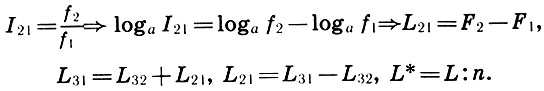
(6.13)

Die Lösung des Oktavteilungsproblems veranlasste Archit sofort zwei Beweise für Irrationalität . Wenn wir versuchen, die Oktave in zwei gleiche Intervalle I zu teilen, dann haben wir (6.8) I ₂₃ = I ₃₁ = I

Bei diesem Verhältnis der Saitenlängen ist jedoch eine deutliche Dissonanz zu hören. Da die Konsonanz durch das Verhältnis der ganzen Zahlen der Form (n + 1): 2 bestimmt wird, legt die Idee nahe, dass die Zahl kann nicht durch das Verhältnis zweier Ganzzahlen ausgedrückt werden, das heißt, es ist irrational.

Der zweite Beweis der Irrationalität weniger musikalisch, aber mathematischer. Um die Quadratwurzel einer Zahl zu finden, die kein vollständiges Quadrat ist, zerlegt Archit sie in zwei ungleiche Faktoren (2 = 1 * 2), bildet dann aus diesen Faktoren das arithmetische Mittel 3/2 und das harmonische Mittel 4/3 und setzt aus diesen Zahlen einen musikalischen Anteil ( 6.7):

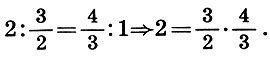
Das Produkt der mittleren Terme dieses Anteils ist gleich einer gegebenen Zahl 2 und ihrer Differenz kleiner als die Differenz der nullten Näherung 2 - 1 = 1. Daher kann als ungefähre Werte betrachtet werden .

(3/2 mit Überschuss, 4/3 mit Mangel].

Nachdem wir das gleiche Verfahren für die ersten Näherungen durchgeführt haben, erhalten wir die zweiten Näherungen:

außerdem

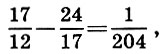
und dann die dritte Annäherung:

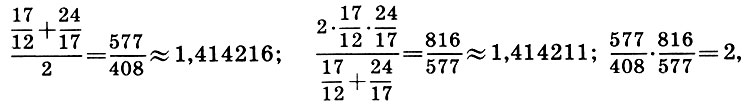
außerdem

1,414216-1,414211 = 0,000005.

Da dieser Vorgang auf unbestimmte Zeit wiederholt werden kann, ist klar, dass die Nummer irrational. Auf dem Weg dorthin sind wir von der Richtigkeit der pythagoreischen Idee überzeugt, dass je größer die ganzen Zahlen in der Beziehung sind, desto genauer drücken sie die irrationale Zahl aus (siehe S. 96). Schließlich erinnere ich mich an diese Bedeutung gleich 1.414213 ... sehen wir, dass die "musikalische" Methode von Archit sehr schnell zum exakten Wert konvergiert und schon die dritte Näherung ergibt fünf korrekte Dezimalstellen!

Aber zurück zu unseren Intervallen. Die Oktave ist also in zwei ungleiche Konsonanzen der fünften und vierten und der fünften unterteilt - durch die vierte und die Dissonanz. Das Tonintervall wurde als Intervall zwischen den benachbarten Tönen (Stufen) in der Höhe bei der Erstellung der pythagoreischen Skala verwendet. Hier ist der Schlüssel zum Aufbau eines Bunds. Laut dem sowjetischen Musikwissenschaftler L. A. Mazel ist das Intervall des fünften, unterteilt in Quart und Ton, das musikalische Hauptelement. 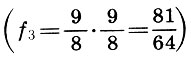Durch die Wahl des Tons als Hauptformationsform müssen die alten Theoretiker nur den Hauptklang beiseite legen dann noch ein Ton und das verbleibende Intervall zwischen dem zweiten Ton und dem Quart-Ton 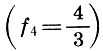Halbton anrufen 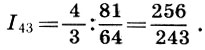Dieser Name ist durchaus gerechtfertigt, da eine Halbierung des Tonintervalls nach Formel (6.12) ergibt 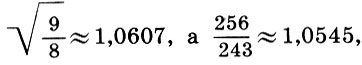ein Halbton ist fast gleich einem halben Ton ^* . So wurde die Grundlage aller antiken griechischen Musik - Tetrachord - eine viersaitige Tonleiter innerhalb eines Viertels erhalten.

^* (Das Tonintervall (Halbton) in der Musiktheorie wird als arithmetische Maßeinheit für Intervalle akzeptiert, und die Intervalle von Ton und Halbton werden im Gegensatz zu ihren Intervallkoeffizienten als große und kleine Sekunden bezeichnet. )

Es ist klar, dass es nur drei Möglichkeiten für die Position des Halbtons innerhalb des Tetrachords gibt, die die Art und den Namen des Tetrachords bestimmt haben:

Dorian: Halbton - Ton - Ton;

Phrygisch: Ton - Halbton - Ton;

Lydian: Ton - Ton - Halbton .

Die Namen der Tetrachorde geben die jeweiligen Regionen Griechenlands und Kleinasiens an, von denen jede in ihrer eigenen Harmonie sang.

Natürlich reichten vier Saiten innerhalb eines Viertels nicht aus, um die Melodie zu leiten, also verbanden sich die Tetrachorde. Wir haben bereits herausgefunden, dass eine Oktave aus zwei Quarts und einem Ton besteht; , , . , , «». «» — . :

1 , 1/2 — , . . , , , (2 — , 3 — , - - - - - - c - o ), — ^* .

^* ( «» , (1 — 1/2 — 1 — 1 — 1/2 — 1 — 1) , — . )

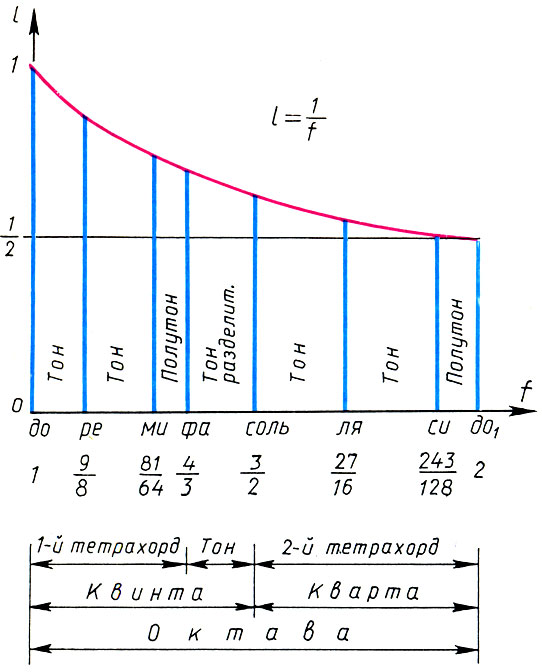Pythagoras-System der lydischen Farbskala und seine mathematischen Eigenschaften

, , , , , . . . f ₁ = 1, o : f ₁ = 1, f ₂ = ⁹ / ₈ , f ₃ = ⁹ / ₈ * ⁹ / ₈ = ⁸¹ / ₆₄ , f ₄ = ⁴ / ₃ . : f ₅ = ³ / ₂f _l = ³ / ₂ , f ₆ = ³ / ₂ f ₂ = ²⁷ / ₁₆ , F ₇ = ³ / ₂ f ₃ = ₂₄₃ / ₁₂₈ , F ₈ = ³ / ₂ f ₄ = 2. Schließlich haben wir für Intervallkoeffizienten aufweisen

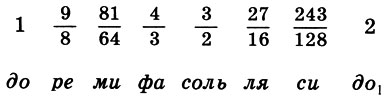(6.14)

Dies ist der Kanon von Pythagoras. Der Legende nach fand der Kanon von Pythagoras erstmals praktische Anwendung bei der Abstimmung der Leier des legendären Orpheus.

. «» , . . , -(-), — - (-). 6 , (- — — ) . , . , , . , , . 1 , , , , — , . .

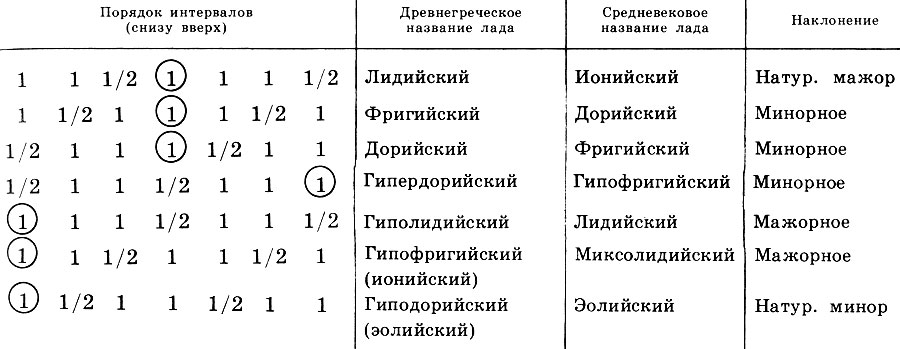Tabelle 1. Die Reihenfolge der Ton- (1) und Halbtonintervalle (1/2) in alten Bünden (von unten nach oben), altgriechischen und mittelalterlichen Namen von Bünden und deren Neigung

Wenn wir uns daran erinnern, dass jetzt nur zwei Bünde dominieren - Dur und Moll, können wir uns nur fragen, wie hoch entwickelt das alte Musikbewusstsein war. Die Griechen füllten jeden Weg mit einem bestimmten ethischen und ästhetischen Inhalt, seinem „Ethos“, und stellten eine klare Verbindung zwischen musikalischen Bildern und Seelenzuständen her. Der Musik wurden magische und sogar medizinische Funktionen zugeschrieben, aber der Musik als Bildungsmittel wurde besondere Bedeutung beigemessen.

Tanzende Menada. Erleichterung

, «» , . , , ,- (. 551-479 . . .), : « , — ». , , , . , , , , . , , , . , . , , . , , «» , , , , .

Aristoteles in der Politik beurteilt Bünde, die vielleicht sogar strenger sind als Platon, und erkennt nur den dorischen Modus als einen Modus an, der die Psyche trainieren kann. Trotzdem nimmt Aristoteles eine detaillierte "ethische" Klassifizierung von Modi vor, wobei Modi unterschieden werden, die ein geistiges Gleichgewicht verursachen (Dorian), im Gegenteil, es verletzen (Hypofrigian - "Tisch" -Modus), den Willen und das Verlangen nach Handeln erregen (Hypodorian - Modus der griechischen Tragödie). einen ekstatischen und ekstatischen Zustand verursachen (Phrygian, Hypolidian).

Eine schöne Beschreibung des „Ethos“ der griechischen Bünde finden wir im Buch des antiken römischen Schriftstellers Apuleius (ca. 124 -?) „Florids“: „Früher gab es einen Flötisten namens Antigenides. Jeder Klang im Spiel dieses Musikers war süß, alle Bünde waren ihm vertraut, und er konnte für Sie nach Ihrer Wahl die Einfachheit des Äolischen Bunds, den Reichtum des Ionischen, die Traurigkeit des Lydischen, die Hochstimmung des Phrygischen und die Militanz von Doria nachstellen. "

Aber hör auf! Gibt es hier einen Widerspruch? Die dorische Stimmung wird als kriegerisch bezeichnet, aber tatsächlich ist es unser Minderjähriger! Da es die dorische Stimmung war, die als wirklich griechisch galt, stellt sich heraus, dass die Hauptfigur der griechischen Musik traurig und minderjährig ist. Für die Griechen ist die dorische Stimmung Ausdruck von Lebhaftigkeit, Fröhlichkeit und sogar Militanz. So erklärt der herausragende zeitgenössische Gelehrte der Antike, der letzte Philosoph des russischen „Silberzeitalters“, Professor A. F. Losev (1893-1988) ^* : „Die griechische Kunst ist eine unveränderliche Lebensbejahung.“ Edle Zurückhaltung und sogar Traurigkeit verlassen den Griechen nicht, selbst wenn er Spaß hat, wenn er fröhlich sein Leben aufbaut, wenn er im Krieg ist und stirbt. "Fröhliche" Bünde ziehen auf die eine oder andere Weise diese schöne, edle, kraftvolle, wichtige und gleichzeitig majestätisch traurige Trauer an - Dorian. Die dorische Stimmung ist der skulpturale Stil der griechischen Musik ... Die gesamte griechische Skulptur ist also so nachdenklich, traurig und edel. “

^* ( Das Schicksal von Aleksei Fedorovich Losev ist glücklich und tragisch. Er ist glücklich, weil Losev bis zum letzten Tag seines 95-jährigen Lebens eine erstaunliche Arbeitsfähigkeit bewahrt und es geschafft hat, das Hauptwerk fertigzustellen - die achtbändige „Geschichte der antiken Ästhetik“. Tragisch, weil die anderen acht Bände seiner Werke geschrieben sind Ein halbes Jahrhundert zuvor (1927 - 1930) wurden sie anathematisiert, und der Autor selbst, der illegal unterdrückt wurde, setzte seine philosophische Forschung über den Bau des Weißmeer-Ostsee-Kanals fort, aus der er schrieb: „Ich bin angekettet, wenn meine Seele brodelt ewige und unerschöpfliche Kräfte. “Eines dieser Werke von Losev,„ Musik als Gegenstand der Logik “, könnte als Leitfaden für dieses Buch dienen. Dennoch ist das Schicksal von A. F. Losev glücklich, weil die Manuskripte nicht brennen. Heute ist das große philosophische Erbe von A. F. Losev erlangt seine Wiedergeburt zurück. )

Aber was ist mit dem lydischen Weg? Immerhin ist dies genau unser Hauptfach, während Apuleius es traurig nennt und Platon - Beerdigung! Nun, bei der Beurteilung des lydischen Bundes stimmte Aristoteles Platon nicht zu, fand naive Kindlichkeit und Charme im lydischen Bund und schrieb ihn Bünden zu, die ein geistiges Gleichgewicht verursachen. Im Laufe der Zeit hat der lydische Modus seinen bedauernswerten Charakter verloren, und alte Theoretiker sprachen häufiger über die "süße lydische Melodie" oder die "vielfältige lydische Melodie".

Wir sehen also, dass die Frage nach dem „Ethos“ der Bünde nicht eindeutig gelöst ist und weitgehend von der Tradition bestimmt wird , diesen oder jenen Bund anzuwenden . Und in unserer Zeit unterscheidet der Hörer, der zum Beispiel in einer subtilen und eigenartigen indischen Musik aufgewachsen ist, nicht zwischen Dur und Moll, ganz zu schweigen von ihrem „Ethos“. Natürlich zeichnet sich die Hauptstimmung durch hellere und freudigere Töne aus, und es gibt objektive Gründe dafür, die wir in Kapitel 10 diskutieren werden. Die Realisierung dieser Möglichkeiten hängt jedoch von einer Vielzahl anderer Faktoren ab (Tempo, Rhythmus, Melodiemuster usw.), und daher gibt es diese viele fröhliche, energische Werke in Moll und traurig, brütend in Dur. Erinnern wir uns zumindest an die „pathetische Sonate“ in Moll Beethoven, diesen feurig-leidenschaftlichen Monolog des Helden, der einen heftigen Kampf und sogar den Tod fordert. Viele Künstler haben viele Beinamen für diese Sonate aufgegriffen (obwohl vielleicht das beste von ihnen - erbärmlich - Beethoven selbst gehört), aber es kann nicht nur als traurig bezeichnet werden - Moll. Im Gegenteil, Nocturne Nr. 2 Op. Der 9. flache Major von Chopin ist von einer Stimmung sanfter Träumereien durchdrungen. Dies sind verschwommene, traurige Erinnerungen des Autors, aber keineswegs ein fröhliches Major-Stück. Lassen Sie uns abschließend versuchen, einige Worte über das "Ethos der Intervalle" zu sagen, da das vorliegende Kapitel der Analyse musikalischer Intervalle gewidmet ist. Wir werden es versuchen, weil dieses Thema noch kontroverser und unentwickelter ist als das "Ethos der Bünde". Und doch ...

Bisher haben wir nichts über die „perfekteste Konsonanz“ gesagt - prima (unisono) (l ₂ / l ₁ = 1, dh zwei Saiten erzeugen einen Klang gleicher Höhe), da dieses Intervall aus mathematischer Sicht nicht von Interesse ist. Im Orchester spielt dieses einfachste Intervall jedoch eine große Rolle und verleiht diesem Klang Volumen und Helligkeit.

Die nächste perfekte Konsonanz ist die Oktave. Gleichzeitig vermittelt die Oktave den Eindruck eines dreidimensionalen Klangs und mit einem sequentiellen Klang ein Gefühl von Geräumigkeit und Breite. Ein hervorragendes Beispiel dafür ist das „Lied vom Mutterland“ des Komponisten I. O. Dunaevsky (1900-1955). In ihrem Refrain ("Von Moskau bis in die Außenbezirke ...") ertönt zweimal eine aufsteigende Oktave (l ₁ / l ₂ = 2), die die Weiten unseres Mutterlandes malt. Hier gibt es nach zwei Oktaven ein aufsteigendes Fünftel. Eine Quinta (l ₁ / l ₂ = 3/2) klingt ebenfalls breit, aber strukturierter und dynamischer als eine Oktave.

Die Melodien vieler revolutionärer Lieder und Hymnen beginnen mit einem Intervall von aufsteigendem Quart (l ₁ / l ₂ = 4/3), zum Beispiel International, Hymne der Sowjetunion, Marseillaise. Hier klingt das Intervall eines Quart entschlossen und aktiv wie ein Aufruf zum Handeln.

Im Sekundenintervall gibt es ein spezielles „Ethos“: Bei gleichzeitigem Klang ist es dissonant und unangenehm, aber bei aufeinanderfolgendem Klang fließt der vorherige in den nächsten über und bildet den natürlichen Fluss der Melodie von einem Klang zum anderen. In einer Melodie werden die Intervalle zwischen zwei Referenztönen häufig in aufeinanderfolgenden zweiten Intervallen gefüllt. Zum Beispiel beginnt das Lied „Eine Birke stand auf dem Feld“ mit einem fünften Intervall, das mit aufeinanderfolgenden Sekunden gefüllt ist und den Eindruck eines ruhigen und stattlichen Flusses der Melodie erweckt, wie stattliche und ruhige Bilder russischer Natur.

Und das unangenehmste und dissonanteste ist das Intervall Triton oder Halboktave (l ₁ / l ₂ = ) Aufgrund seiner Inkonsistenz „veranlasste“ dieses Intervall den Architekten zum „musikalischen Beweis“ der Irrationalität .

Vielen Dank an die Bibliothek für Mathematik für die Digitalisierung des Buches.