Richard Hamming: Kapitel 10. Codierungstheorie - I.

"Ziel dieses Kurses ist es, Sie auf Ihre technische Zukunft vorzubereiten."

Hallo Habr. Erinnern Sie sich an den großartigen Artikel „Sie und Ihre Arbeit“ (+219, 2442 Lesezeichen, 394.000 Lesungen)?

Hamming (ja, ja, selbstüberprüfende und selbstkorrigierende Hamming-Codes ) hat ein ganzes Buch geschrieben, das auf seinen Vorlesungen basiert. Wir übersetzen es, weil der Mann geschäftlich spricht.

In diesem Buch geht es nicht nur um IT, sondern auch um den Denkstil unglaublich cooler Leute. „Dies ist nicht nur eine Anklage für positives Denken. Es beschreibt Bedingungen, die die Chancen erhöhen, gute Arbeit zu leisten. “

Wir haben bereits 28 (von 30) Kapiteln übersetzt. Und wir arbeiten an einer Papierausgabe.

Codierungstheorie - I.

Nachdem wir uns mit Computern und dem Prinzip ihrer Arbeit befasst haben, werden wir uns nun mit dem Thema Information befassen: Wie Computer die Informationen darstellen, die wir verarbeiten möchten. Die Bedeutung eines Zeichens kann davon abhängen, wie es verarbeitet wird. Die Maschine hat keine spezifische Bedeutung für das verwendete Bit. Bei der Erörterung der Geschichte der Software, Kapitel 4, haben wir eine synthetische Programmiersprache betrachtet, in der der Code der Unterbrechungsanweisung mit dem Code anderer Anweisungen übereinstimmte. Diese Situation ist typisch für die meisten Sprachen, die Bedeutung der Anweisung wird durch das entsprechende Programm bestimmt.

Um das Problem der Darstellung von Informationen zu vereinfachen, betrachten wir das Problem der Übertragung von Informationen von Punkt zu Punkt. Diese Frage bezieht sich auf die Frage der Informationen zur Erhaltung. Die Probleme bei der zeitlichen und räumlichen Übertragung von Informationen sind identisch. Abbildung 10.1 zeigt ein Standardmodell für die Übertragung von Informationen.



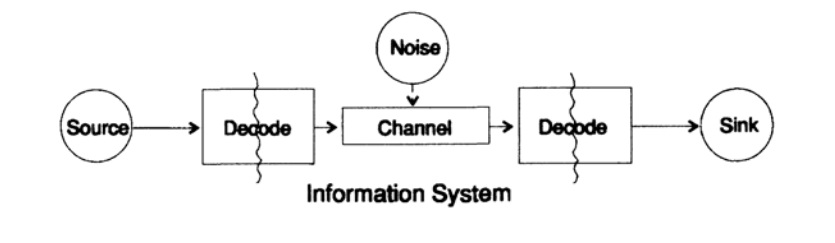Abbildung 10.1

Links in Abbildung 10.1 befindet sich die Informationsquelle. Bei der Betrachtung des Modells ist uns die Art der Quelle egal. Es kann sich um eine Reihe von Symbolen des Alphabets, Zahlen, mathematischen Formeln, Noten, Symbolen handeln, mit denen wir Tanzbewegungen darstellen können - die Art der Quelle und die Bedeutung der darin gespeicherten Symbole sind nicht Teil des Übertragungsmodells. Wir betrachten nur die Informationsquelle, mit einer solchen Einschränkung erhalten wir eine leistungsfähige, allgemeine Theorie, die auf viele Bereiche ausgedehnt werden kann. Es ist eine Abstraktion von vielen Anwendungen.

Als Shannon Ende der 1940er Jahre die Informationstheorie entwickelte, glaubte man, dass sie als Kommunikationstheorie bezeichnet werden sollte, bestand jedoch auf dem Begriff Information. Dieser Begriff ist zu einer ständigen Ursache für zunehmendes Interesse und ständige Enttäuschung in der Theorie geworden. Die Ermittler wollten ganze "Informationstheorien" aufbauen, sie degenerierten zu einer Theorie einer Reihe von Charakteren. Zurück zum Übertragungsmodell haben wir eine Datenquelle, die für die Übertragung codiert werden muss.

Der Encoder besteht aus zwei Teilen, der erste Teil wird als Quellcodierer bezeichnet, der genaue Name hängt vom Quellentyp ab. Quellen verschiedener Datentypen entsprechen verschiedenen Arten von Codierern.

Der zweite Teil des Codierungsprozesses wird als Kanalcodierung bezeichnet und hängt von der Art des Kanals zum Übertragen von Daten ab. Somit stimmt der zweite Teil des Codierungsprozesses mit der Art des Übertragungskanals überein. Bei Verwendung von Standardschnittstellen werden Daten von der Quelle zunächst gemäß den Anforderungen der Schnittstelle und dann gemäß den Anforderungen des verwendeten Datenkanals codiert.

Gemäß dem Modell in Abb. 10.1 ist der Datenkanal „zusätzlichem Zufallsrauschen“ ausgesetzt. Alle Geräusche im System werden zu diesem Zeitpunkt kombiniert. Es wird angenommen, dass der Codierer alle Zeichen ohne Verzerrung akzeptiert und der Decodierer seine Funktion fehlerfrei ausführt. Dies ist eine Idealisierung, aber für viele praktische Zwecke ist sie der Realität nahe.

Die Decodierungsphase besteht ebenfalls aus zwei Stufen: Kanalstandard, Standarddatenempfänger. Am Ende der Datenübertragung wird an den Verbraucher übermittelt. Auch hier denken wir nicht darüber nach, wie der Verbraucher diese Daten interpretiert.

Wie bereits erwähnt, präsentiert ein Datenübertragungssystem, beispielsweise Telefonnachrichten, Radio- und Fernsehprogramme, Daten in Form eines Satzes von Zahlen in den Registern eines Computers. Ich wiederhole noch einmal: Die Übertragung im Raum unterscheidet sich nicht von der Übertragung in der Zeit oder dem Speichern von Informationen. Haben Sie Informationen, die nach einer Weile benötigt werden, müssen diese verschlüsselt und in der Datenspeicherquelle gespeichert werden. Bei Bedarf werden Informationen dekodiert. Wenn das Codierungs- und Decodierungssystem dasselbe ist, übertragen wir Daten unverändert über den Übertragungskanal.

Der grundlegende Unterschied zwischen der vorgestellten Theorie und der in der Physik üblichen Theorie besteht in der Annahme, dass in der Quelle und im Empfänger kein Rauschen vorhanden ist. Tatsächlich treten Fehler in jedem Gerät auf. In der Quantenmechanik tritt Rauschen in jedem Stadium nach dem Unsicherheitsprinzip und nicht als Ausgangsbedingung auf; In jedem Fall entspricht das Konzept des Rauschens in der Informationstheorie nicht einem ähnlichen Konzept in der Quantenmechanik.
Zur Bestimmtheit werden wir weiter die binäre Form der Datendarstellung im System betrachten. Andere Formulare werden auf ähnliche Weise verarbeitet. Der Einfachheit halber werden wir sie nicht berücksichtigen.

Wir beginnen unsere Betrachtung von Systemen mit codierten Zeichen variabler Länge, wie im klassischen Morsecode von Punkten und Strichen, in denen häufig vorkommende Zeichen kurz und seltene lang sind. Mit diesem Ansatz können Sie eine hohe Codeeffizienz erzielen. Beachten Sie jedoch, dass der Morsecode ternär und nicht binär ist, da er ein Leerzeichen zwischen Punkten und Strichen enthält. Wenn alle Zeichen im Code gleich lang sind, wird ein solcher Code als Blockcode bezeichnet.

Die erste offensichtliche notwendige Eigenschaft des Codes ist die Fähigkeit, die Nachricht in Abwesenheit von Rauschen eindeutig zu decodieren. Zumindest scheint dies die gewünschte Eigenschaft zu sein, obwohl diese Anforderung in einigen Situationen vernachlässigt werden kann. Die Daten vom Übertragungskanal für den Empfänger sehen aus wie ein Strom von Zeichen aus Nullen und Einsen.

Wir nennen zwei benachbarte Zeichen eine doppelte Erweiterung, drei benachbarte Zeichen eine dreifache Erweiterung, und im allgemeinen Fall sieht der Empfänger, wenn wir N Zeichen weiterleiten, Ergänzungen zum Basiscode von N Zeichen. Der Empfänger, der den Wert von N nicht kennt, muss den Stream in Broadcast-Blöcke aufteilen. Mit anderen Worten, der Empfänger sollte in der Lage sein, den Stream eindeutig zu zerlegen, um die ursprüngliche Nachricht wiederherzustellen.

Stellen Sie sich ein Alphabet mit einer kleinen Anzahl von Zeichen vor, normalerweise sind Alphabete viel größer. Alphabete von Sprachen beginnen mit 16 bis 36 Zeichen, einschließlich Groß- und Kleinbuchstaben, Zahlenzeichen und Interpunktion. Zum Beispiel in der ASCII-Tabelle 128 = 2 ^ 7 Zeichen.
Stellen Sie sich einen speziellen Code vor, der aus 4 Zeichen s1, s2, s3, s4 besteht

s1 = 0; s2 = 00; s3 = 01; s4 = 11.

Wie soll der Empfänger den nächsten empfangenen Ausdruck interpretieren?

0011 ?

Wie s1s1s4 oder wie s2s4 ?

Sie können diese Frage nicht eindeutig beantworten. Dieser Code wird definitiv nicht dekodiert und ist daher unbefriedigend. Code andererseits

s1 = 0; s2 = 10; s3 = 110; s4 = 111

dekodiert die Nachricht auf einzigartige Weise. Nehmen Sie eine beliebige Zeichenfolge und überlegen Sie, wie der Empfänger sie dekodiert. Sie müssen einen Dekodierungsbaum gemäß dem Formular in Abbildung 10.II erstellen. String

1101000010011011100010100110 ...

kann in Zeichenblöcke unterteilt werden

110, 10, 0, 10, 0, 110, 111, 0, 0, 0, 10, 10, 0, 110, ...

gemäß der folgenden Regel zum Erstellen eines Dekodierungsbaums:

Wenn Sie sich oben im Baum befinden, lesen Sie das nächste Zeichen. Wenn Sie ein Blatt eines Baumes erreichen, konvertieren Sie die Sequenz in ein Zeichen und kehren zum Anfang zurück.

Der Grund für die Existenz eines solchen Baums ist, dass kein Zeichen ein Präfix des anderen ist, sodass Sie immer wissen, wann Sie zum Anfang des Dekodierungsbaums zurückkehren müssen.

Beachten Sie Folgendes. Erstens ist das Decodieren ein strikter Stream-Prozess, bei dem jedes Bit nur einmal untersucht wird. Zweitens enthalten die Protokolle normalerweise Zeichen, die eine Markierung für das Ende des Decodierungsprozesses darstellen und erforderlich sind, um das Ende einer Nachricht anzuzeigen.

Die Nichtverwendung eines nachgestellten Zeichens ist ein häufiger Fehler beim Code-Design. Natürlich können Sie einen konstanten Dekodierungsmodus bereitstellen. In diesem Fall wird das nachfolgende Zeichen nicht benötigt.



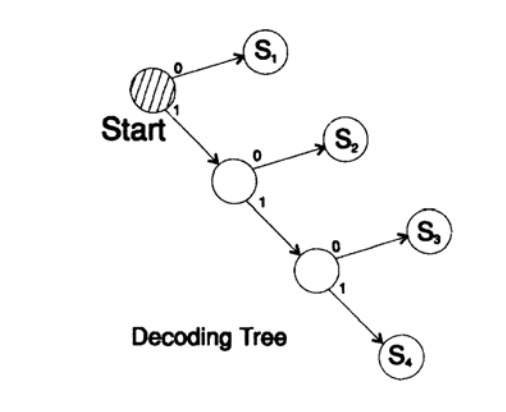Abbildung 10.II

Die nächste Frage sind Codes für die (sofortige) Stream-Decodierung. Betrachten Sie den Code, der durch Anzeigen von Zeichen aus dem vorherigen Code erhalten wurde

s1 = 0; s2 = 01; s3 = 011; s4 = 111.

Angenommen, wir erhalten die Sequenz 011111 ... 111 . Die einzige Möglichkeit, den Nachrichtentext zu dekodieren, besteht darin, Bits vom Ende von 3 in einer Gruppe zu gruppieren und Gruppen mit einer führenden Null vor Einsen auszuwählen, wonach Sie dekodieren können. Ein solcher Code wird auf einzigartige Weise dekodiert, aber nicht sofort! Zum Entschlüsseln müssen Sie auf das Ende der Übertragung warten! In der Praxis eliminiert dieser Ansatz die Decodierungsrate (Macmillan-Theorem), daher ist es notwendig, nach Methoden der sofortigen Decodierung zu suchen.

Betrachten Sie zwei Möglichkeiten, um dasselbe Zeichen zu codieren: Si:

s1 = 0; s2 = 10; s3 = 110; s4 = 1110, s5 = 1111,

Der Decodierungsbaum dieser Methode ist in Abbildung 10.III dargestellt.



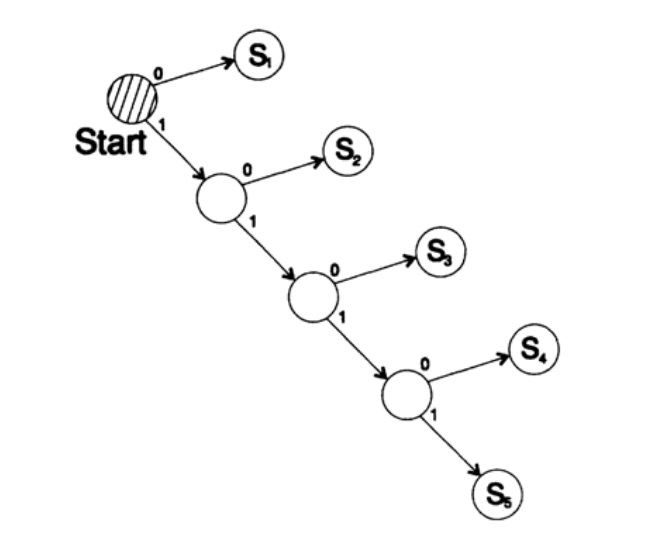Abbildung 10.III

Zweiter Weg

s1 = 00; s2 = 01; s3 = 100; s4 = 110, s5 = 111 ,

Der Dekodierungsbaum dieser Pflege ist in Abbildung 10.IV dargestellt.

Der naheliegendste Weg, um die Codequalität zu messen, ist die durchschnittliche Länge für eine Reihe von Nachrichten. Hierzu ist es erforderlich, die Codelänge jedes Zeichens multipliziert mit der entsprechenden Wahrscheinlichkeit des Auftretens von pi zu berechnen. Somit wird die Länge des gesamten Codes erhalten. Die Formel für die durchschnittliche Länge L des Codes für ein Alphabet mit q Zeichen lautet wie folgt



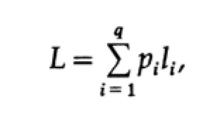
Dabei ist pi die Wahrscheinlichkeit des Auftretens des Symbols si, li die entsprechende Länge des codierten Symbols. Für einen effizienten Code sollte der Wert von L so klein wie möglich sein. Wenn P1 = 1/2, p2 = 1/4, p3 = 1/8, p4 = 1/16 und p5 = 1/16, erhalten wir für Code # 1 den Wert für die Codelänge



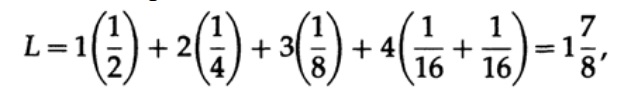
Und für Code # 2



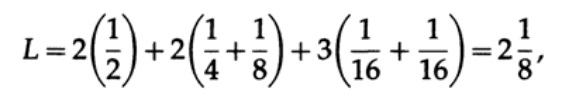
Die erhaltenen Werte geben die Präferenz des ersten Codes an.
Wenn alle Wörter im Alphabet die gleiche Wahrscheinlichkeit des Auftretens haben, ist der zweite Code vorzuziehen. Zum Beispiel mit pi = 1/5 die Codelänge # 1



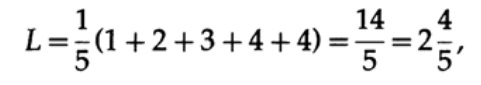
und Codelänge # 2



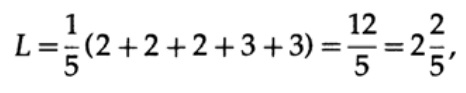
Dieses Ergebnis zeigt eine Präferenz für 2 Codes. Daher ist es bei der Entwicklung von „gutem“ Code erforderlich, die Wahrscheinlichkeit des Auftretens von Zeichen zu berücksichtigen.



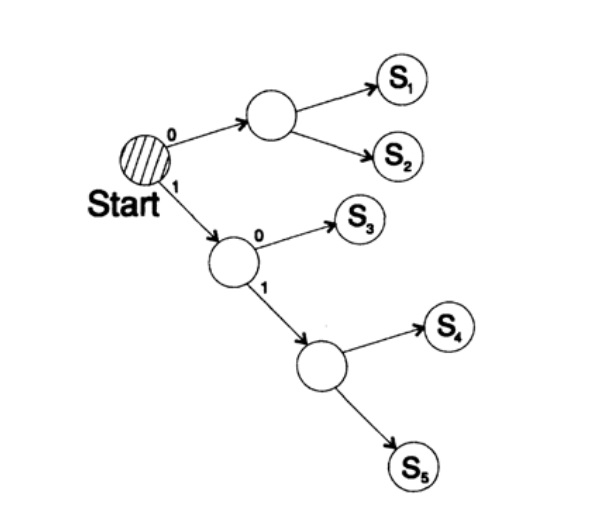Abbildung 10.IV.



Abbildung 10.V

Betrachten Sie die Kraft-Ungleichung, die den Grenzwert der Länge des Symbolcodes li bestimmt. In Basis 2 wird die Ungleichung dargestellt als



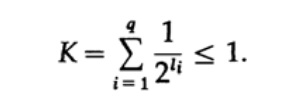
Diese Ungleichung legt nahe, dass das Alphabet nicht zu viele kurze Zeichen enthalten kann, da sonst die Summe ziemlich groß ist.

Um die Kraft-Ungleichung für jeden schnell eindeutigen decodierten Code zu beweisen, konstruieren wir einen Decodierungsbaum und wenden die Methode der mathematischen Induktion an. Wenn ein Baum ein oder zwei Blätter hat, wie in Abbildung 10.V gezeigt, ist die Ungleichung zweifellos wahr. Wenn der Baum mehr als zwei Blätter hat, teilen wir den Baum mit dem langen m in zwei Teilbäume auf. Nach dem Induktionsprinzip nehmen wir an, dass die Ungleichung für jeden Zweig der Höhe m -1 oder weniger gilt. Nach dem Prinzip der Induktion wird auf jeden Zweig eine Ungleichung angewendet. Bezeichnen Sie die Länge der Codes der Zweige K 'und K' '. Wenn zwei Zweige eines Baumes kombiniert werden, erhöht sich die Länge jedes Zweigs um 1, daher besteht die Länge des Codes aus den Summen K '/ 2 und K' '/ 2,



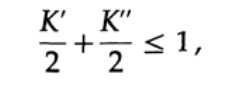
Der Satz ist bewiesen.

Betrachten Sie den Beweis von Macmillans Theorem. Wir wenden die Kraft-Ungleichung an, um Codes fadenlos zu dekodieren. Der Beweis basiert auf der Tatsache, dass für jede Zahl K> 1 die n-te Potenz der Zahl offensichtlich mehr als eine lineare Funktion von n ist, wobei n eine ziemlich große Zahl ist. Wir erhöhen die Kraft-Ungleichung auf die n-te Potenz und präsentieren den Ausdruck als Summe



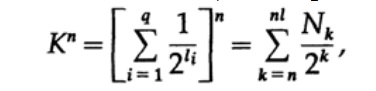
wobei Nk die Anzahl der Zeichen der Länge k ist, beginnt die Summierung mit der minimalen Länge der n-ten Darstellung des Zeichens und endet mit der maximalen Länge nl, wobei l die maximale Länge des codierten Zeichens ist. Aus dem Erfordernis einer eindeutigen Decodierung folgt daraus. Der Betrag wird als dargestellt



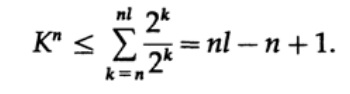
Wenn K> 1 ist, muss n groß genug sein, damit die Ungleichung falsch wird. Daher ist k <= 1; Macmillans Theorem ist bewiesen.

Betrachten Sie einige Beispiele für die Anwendung der Kraft-Ungleichung. Kann ein eindeutig decodierter Code mit den Längen 1, 3, 3, 3 existieren? Ja seitdem



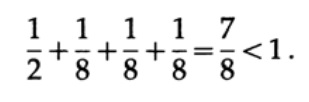
Was ist mit den Längen 1, 2, 2, 3? Berechnen Sie nach der Formel



Ungleichheit verletzt! Dieser Code enthält zu viele kurze Zeichen.

Komma-Codes sind Codes, die aus Zeichen 1 bestehen und mit einem Zeichen 0 enden, mit Ausnahme des letzten Zeichens, das aus allen besteht. Einer der Sonderfälle ist Code.

s1 = 0; s2 = 10; s3 = 110; s4 = 1110; s5 = 11111.

Für diesen Code erhalten wir den Ausdruck für die Kraft-Ungleichung



In diesem Fall erreichen wir Gleichheit. Es ist leicht zu erkennen, dass bei Punktcodes die Kraft-Ungleichung in Gleichheit ausartet.

Beim Erstellen eines Codes müssen Sie auf die Menge an Kraft achten. Wenn die Kraftmenge 1 überschreitet, ist dies ein Signal für die Notwendigkeit, ein Zeichen mit einer anderen Länge aufzunehmen, um die durchschnittliche Codelänge zu verringern.

Es sollte beachtet werden, dass Krafts Ungleichung nicht bedeutet, dass dieser Code eindeutig decodierbar ist, sondern dass es einen Code mit Zeichen dieser Länge gibt, der eindeutig decodiert ist. Um einen eindeutigen decodierten Code zu erstellen, können Sie die entsprechende Länge in Bit li mit einer Binärzahl versehen. Zum Beispiel erhalten wir für die Längen 2, 2, 3, 3, 4, 4, 4, 4 die Kraft-Ungleichung



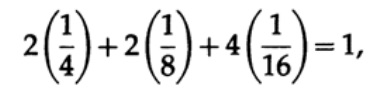
Daher kann ein solcher eindeutiger decodierter Stream-Code existieren.

s1 = 00; s2 = 01; s3 = 100; s4 = 101;

s5 = 1100; s6 = 1101; s7 = 1110; s8 = 1111;

Ich möchte darauf achten, was tatsächlich passiert, wenn wir Ideen austauschen. Zum Beispiel möchte ich zu diesem Zeitpunkt die Idee von meinem Kopf auf Ihren übertragen. Ich spreche einige Wörter aus, durch die Sie, wie ich glaube, diese Idee verstehen (verstehen) können.

Aber wenn Sie wenig später Ihrem Freund diese Idee vermitteln möchten, werden Sie mit ziemlicher Sicherheit ganz andere Worte aussprechen. Tatsächlich ist die Bedeutung oder Bedeutung nicht in bestimmten Wörtern enthalten. Ich habe einige Wörter verwendet, und Sie können ganz andere verwenden, um dieselbe Idee zu vermitteln. Somit können verschiedene Wörter die gleiche Information vermitteln. Sobald Sie Ihrem Gesprächspartner jedoch mitteilen, dass Sie die Nachricht nicht verstehen, wählt der Gesprächspartner in der Regel einen anderen Satz von Wörtern aus, den zweiten oder sogar den dritten, um die Bedeutung zu vermitteln. Daher sind die Informationen nicht in einer Reihe spezifischer Wörter enthalten. Sobald Sie diese oder jene Wörter erhalten, erledigen Sie viel Arbeit, wenn Sie die Wörter in die Idee übersetzen, die der Gesprächspartner Ihnen vermitteln möchte.

Wir lernen, Wörter auszuwählen, um uns an den Gesprächspartner anzupassen. In gewissem Sinne wählen wir Wörter, die unseren Gedanken und dem Rauschpegel im Kanal entsprechen, obwohl ein solcher Vergleich das Modell, das ich zur Darstellung des Rauschens im Decodierungsprozess verwende, nicht genau widerspiegelt. In großen Organisationen besteht ein ernstes Problem darin, dass der Gesprächspartner nicht hören kann, was eine andere Person gesagt hat. In leitenden Positionen hören Mitarbeiter, was sie „hören wollen“. In einigen Fällen müssen Sie sich daran erinnern, wenn Sie die Karriereleiter hinaufsteigen. Die Darstellung von Informationen in formaler Form spiegelt teilweise Prozesse aus unserem Leben wider und hat weit über die Grenzen formaler Regeln in Computeranwendungen hinaus breite Anwendung gefunden.

Fortsetzung folgt...

Wer bei der Übersetzung, dem Layout und der Veröffentlichung des Buches helfen möchte, schreibt eine persönliche E-Mail oder eine E-Mail an magisterludi2016@yandex.ru

Übrigens haben wir auch die Übersetzung eines anderen coolen Buches veröffentlicht - "Die Traummaschine: Die Geschichte der Computerrevolution" )