Kapselneurale Netze

Im Jahr 2017 veröffentlichte Jeffrey Hinton (einer der Begründer des Ansatzes der Fehlerrückübertragung) einen Artikel, in dem Kapsel-Neuronale Netze beschrieben und ein Algorithmus für das dynamische Routing zwischen Kapseln vorgeschlagen wurden, um die vorgeschlagene Architektur zu vermitteln.

Klassische Faltungs-Neuronale Netze haben Nachteile. Die interne Darstellung von Faltungsdaten neuronaler Netze berücksichtigt keine räumlichen Hierarchien zwischen einfachen und komplexen Objekten. Wenn also die Augen, die Nase und die Lippen eines Faltungsnetzwerks zufällig im Bild angezeigt werden, ist dies ein deutliches Zeichen für das Vorhandensein eines Gesichts. Und die Rotation des Objekts beeinflusst die Erkennungsqualität, während das menschliche Gehirn dieses Problem leicht löst.


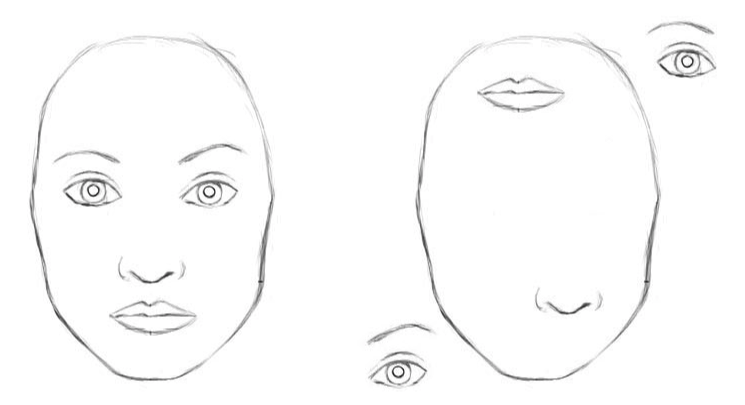
Für ein neuronales Faltungsnetzwerk sind 2 Bilder ähnlich [2]


Tausende von Beispielen werden benötigt, um die Objekterkennung aus verschiedenen CNN-Winkeln zu trainieren.


Kapselnetzwerke reduzieren den Erkennungsfehler eines Objekts aus einem anderen Winkel um 45%.

Verschreibungspflichtige Kapseln

Kapseln kapseln Informationen über den Zustand der Funktion, die in Vektorform vorliegen. Kapseln codieren die Wahrscheinlichkeit, ein Objekt zu erkennen, als die Länge des Ausgabevektors. Der Status der erkannten Funktion wird als die Richtung codiert, in die der Vektor zeigt („Instanzerstellungsparameter“). Wenn sich die erkannte Funktion durch das Bild bewegt oder sich der Zustand des Bildes ändert, bleibt die Wahrscheinlichkeit unverändert (die Länge des Vektors ändert sich nicht), aber die Ausrichtung ändert sich.

Stellen Sie sich vor, eine Kapsel erkennt ein Gesicht in einem Bild und gibt einen 3D-Vektor mit einer Länge von 0,99 aus. Bewegen Sie dann das Gesicht im Bild. Der Vektor dreht sich in seinem Raum und stellt einen sich ändernden Zustand dar. Seine Länge bleibt jedoch fest, da die Kapsel sicher ist, dass sie ein Gesicht erkannt hat.



Unterschiede zwischen Kapseln und Neuronen. [2]

Ein künstliches Neuron kann in drei Schritten beschrieben werden:

1. Skalargewichtung von Eingabeskalaren
2. Summe der gewichteten Eingabeskalare
3. nichtlineare Skalartransformation.

Die Kapsel hat zusätzlich zur neuen Phase der affinen Transformation der Eingabe die Vektorformen der obigen 3 Schritte:

1. Matrixmultiplikation von Eingangsvektoren
2. Skalargewichtung von Eingabevektoren
3. Summe der gewichteten Eingabevektoren
4. Vektor-Nichtlinearität.

Eine weitere in CapsNet eingeführte Innovation ist eine neue nichtlineare Aktivierungsfunktion, die einen Vektor nimmt und dann seine Länge nicht mehr als 1 "ausgibt", aber die Richtung nicht ändert.



Die rechte Seite der Gleichung (blaues Rechteck) skaliert den Eingabevektor so, dass der Vektor eine Blocklänge hat, und die linke Seite (rotes Rechteck) führt eine zusätzliche Skalierung durch.

Das Kapsel-Design basiert auf der Konstruktion eines künstlichen Neurons, erweitert es jedoch auf eine Vektorform, um leistungsfähigere repräsentative Fähigkeiten bereitzustellen. Matrixgewichte werden auch eingeführt, um hierarchische Beziehungen zwischen Merkmalen verschiedener Schichten zu codieren. Die Äquivarianz der neuronalen Aktivität wird in Bezug auf Änderungen der Eingabedaten und die Invarianz der Wahrscheinlichkeiten der Erkennung von Zeichen erreicht.

Dynamisches Routing zwischen Kapseln

Der dynamische Routing-Algorithmus [1].

Die erste Zeile besagt, dass diese Prozedur Kapseln auf der unteren Ebene l und ihre Ausgaben u_hat sowie die Anzahl der Routing-Iterationen r nimmt. Die letzte Zeile besagt, dass der Algorithmus die Ausgabe einer übergeordneten Kapsel v_j erzeugt.

Die zweite Zeile enthält einen neuen Koeffizienten b_ij, den wir bisher noch nicht gesehen haben. Dieser Koeffizient ist ein temporärer Wert, der iterativ aktualisiert wird. Nach Abschluss der Prozedur wird sein Wert in c_ij gespeichert. Zu Beginn des Trainings wird der Wert von b_ij auf Null initialisiert.

Zeile 3 besagt, dass die Schritte 4 bis 7 r-mal wiederholt werden.
Der Schritt in Zeile 4 berechnet den Wert des Vektors c_i, der alle Routinggewichte für die untere Kapsel i darstellt.

Nachdem die Gewichte c_ij für die Kapseln der unteren Ebene berechnet wurden, gehen Sie zu Zeile 5, wo wir uns die Kapseln einer höheren Ebene ansehen. Dieser Schritt berechnet eine lineare Kombination von Eingabevektoren, die unter Verwendung der im vorherigen Schritt definierten Routing-Koeffizienten c_ij gewichtet wurden.

Dann durchlaufen in Zeile 6 die Vektoren des letzten Schritts eine nichtlineare Transformation, die die Richtung des Vektors garantiert, aber seine Länge sollte 1 nicht überschreiten. Dieser Schritt erzeugt den Ausgabevektor v_j für alle höheren Ebenen der Kapsel. [2]
Die Grundidee ist, dass die Ähnlichkeit zwischen Eingabe und Ausgabe als Skalarprodukt zwischen Eingabe und Ausgabe der Kapsel gemessen wird und sich dann der Routing-Koeffizient ändert. Es wird empfohlen, drei Routing-Iterationen zu verwenden.

Fazit

Kapselneurale Netze sind eine vielversprechende Architektur neuronaler Netze, die die Bilderkennung bei sich ändernden Winkeln und hierarchischen Strukturen verbessert. Kapselneurale Netze werden durch dynamisches Routing zwischen Kapseln trainiert. Kapselnetzwerke reduzieren den Erkennungsfehler eines Objekts aus einem anderen Winkel um 45% im Vergleich zu CNN.