Was ist mit dem Fermi-Paradoxon passiert?

Das Fermi-Paradoxon ist, dass die Wahrscheinlichkeit einer außerirdischen Zivilisation normalerweise ziemlich hoch geschätzt wird und es keine Anzeichen für ihre Existenz gibt. Kürzlich erschien ein Vorabdruck von Sanders und Co-Autoren von „Dissolving the Fermi paradox“ auf arxiv, den sie bereits als Aufhebung dieses Paradoxons (wahr) interpretiert haben, müßiges Geschwätz ohne Daten (eher wahr, aber wahr für das Fermi-Paradoxon im Allgemeinen und nicht nur für diesen Artikel). und als Beweis für die Nichtexistenz von Außerirdischen und / oder niedrigem L (Unwahrheit). In diesem Artikel werden wir versuchen herauszufinden, was der Preprint tatsächlich enthält.

Was ist los?

Zuallererst die Drake-Gleichung selbst. Es wird auf der KDPV vorgestellt; Der letzte Faktor ist ein Witz, und der Rest sollte wie folgt verstanden werden: im beobachtbaren Universum (oder unserer Galaxie oder einem anderen Raumvolumen) $$ Sterne. Jeder Stern mit Wahrscheinlichkeit $$ hat Planeten. Jeder dieser Planeten ist wahrscheinlich $$ befindet sich in der Goldlöckchen-Zone, hat eine geeignete chemische Zusammensetzung usw. Auf jedem Planeten, der möglicherweise in der Lage ist, das Leben mit Wahrscheinlichkeit zu erhalten $$ (pro Zeiteinheit) entsteht ein Leben, das wahrscheinlich ist $$ erreicht Vernünftigkeit und mit Wahrscheinlichkeit $$ meldet sich. Und schließlich existiert jede intelligente Spezies, die entsteht $$ Jahre von der Geburt bis zum Aussterben. Wenn Sie all dies multiplizieren, erhalten Sie die Anzahl der intelligenten Arten in diesem Bereich.

Die Zeit zwischen dem Ursprung des Geistes und dem Erscheinen einer wahrnehmbaren Zivilisation in interstellaren Entfernungen wird vernachlässigt. Im Fall der Erde sind beispielsweise Milliarden von Jahren vom Erscheinen des Planeten zum Erscheinen des Lebens und vom Erscheinen des Lebens zum Erscheinen der Art Homo sapiens vergangen. Der technologische Fortschritt ist unvergleichlich schneller - das Auftauchen des Homo sapiens aus der Botschaft von Arecibo trennt weniger als zehn Millionen Jahre. Die interstellare Kolonisierung hat noch nicht begonnen, aber dies ist auch der schlimmste Fall von ein paar Millionen Jahren. Verglichen mit den vortechnologischen Stadien - innerhalb der Fehlergrenze.

Was, um es taktvoller auszudrücken, ziemlich hoch ist . Von der Größenordnung für die Anzahl der Sterne und der Wahrscheinlichkeit, Planeten zu haben, bis zu 200 Größenordnungen (zweihundert Größenordnungen, unterscheiden sich die Schätzungen in $$ Zeiten) für die Wahrscheinlichkeit der Abiogenese. Diese undankbare Aufgabe besteht darin, die Wahrscheinlichkeiten anhand einer einzelnen Beobachtung zu bewerten. Wissenschaftler veröffentlichten jedoch verschiedene Schätzungen $$ und kam meistens zu dem Schluss, dass $$ und sogar $$ . Was in der Tat das Fermi-Paradoxon ist: Nach unseren besten Schätzungen muss es andere intelligente Rassen in der Galaxie geben, und es gab keine verlässlichen Beweise für ihre Existenz.

Das Problem liegt offensichtlich nicht in der Galaxie: Wenn sich die Schätzungen von der beobachteten Realität unterscheiden, ist dies für die Schätzungen umso schlimmer. Entweder wird einer der Parameter stark überschätzt ( und Gott segne uns, wenn es L ist ), oder wir denken irgendwie falsch. Sandberg et al. Befürworten nur die neueste Version.

Und wie zählt man richtig?

Es scheint eine Handvoll reeller Zahlen zu multiplizieren - nicht Newtons Binomial. Der Haken ist, dass in einer solchen Situation die Multiplikation von Zahlen von der Annahme abhängt, dass sie uns sowieso genau bekannt sind. Wie wir oben gesehen haben, ist diese Annahme sehr weit von der Realität entfernt.

Betrachten Sie ein vereinfachtes Beispiel: Lassen Sie die Drake-Gleichung neun Parameter haben und alle neun sind gleichmäßig im Bereich verteilt $$ . Die beste Punktschätzung für jeden dieser Parameter ist 0,1 und ihr Produkt ergibt eine Wahrscheinlichkeit von einer Zivilisation pro Milliarde Sterne. In der Galaxie aus $$ Etwa 100 Zivilisationen sollten in den Sternen erscheinen, und die Wahrscheinlichkeit, dass dies niemals passieren wird - $$ . Solche Wahrscheinlichkeiten werden normalerweise mit Sätzen wie „wenn jedes Atom in <einem sehr großen Ding wie dem Sonnensystem> für <eine sehr lange Zeit wie sein Alter> dargestellt wird“ dargestellt. Was in diesem Fall durchaus angemessen klingt, aber tatsächlich ist es unmöglich, eine solche Nullhypothese nicht abzulehnen. Das Fermi-Paradoxon erreicht seine volle Höhe.

Wenn wir keine Punktschätzungen verwenden und für jeden Parameter einen Zufallswert aus dem entsprechenden Bereich verwenden, ist die Galaxie in 21,45% der Simulationen leer. Die Tatsache, dass etwas mit einer Wahrscheinlichkeit von etwas mehr als einem Fünftel passiert ist, ist keineswegs paradox. Dies ist etwas weniger wahrscheinlich, dass ein Paar Könige alle anderen Hände an einem Hold'em-Tisch mit 9 Spielern schlägt , und mit Pocket Kings gehe ich persönlich zum frühestmöglichen Zeitpunkt All-In.

Dieselbe Logik kann auf reale Schätzungen der Parameter der Drake-Gleichung angewendet werden. Wenn Sie sie aus der Literatur sammeln und die Simulation ausführen, erhalten Sie das folgende Bild:



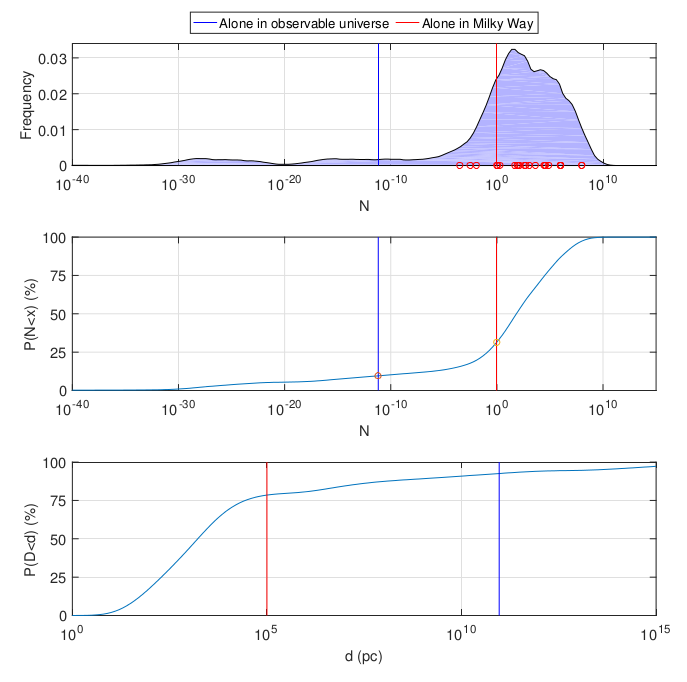
Von oben nach unten: die Wahrscheinlichkeitsdichtefunktion für die Anzahl der Zivilisationen in unserer Galaxie, die kumulative Verteilungsdichte dafür, die kumulative Verteilungsdichte der Entfernung zur nächsten beobachtbaren Zivilisation in Parsec. Alles ist logarithmisch. Die roten und blauen Linien zeigen die Wahrscheinlichkeit an, dass wir die einzige Zivilisation in unserer Galaxie und im beobachtbaren Universum sind. Kreise in der oberen Grafik - normalisierte literarische Bewertungen $$ .

Insgesamt ist das Ergebnis eher optimistisch: Die größte Wahrscheinlichkeitsdichte liegt in der Vielzahl der Zivilisationen (durchschnittlich 53 Millionen, Median 100). Für die Zwecke des Fermi-Paradoxons sind die Zahlen jedoch ungefähr dieselben wie in einem vereinfachten Beispiel: Mit einer Wahrscheinlichkeit von zwanzig Prozent oder so enthält die Milchstraße nur eine Zivilisation (unsere). Übrigens eine eher kontraintuitive Konsequenz: Die Wahrscheinlichkeit, dass die Milchstraße, ohne die Erde , genau eine Zivilisation enthält (außer unserer), ist praktisch dieselbe.

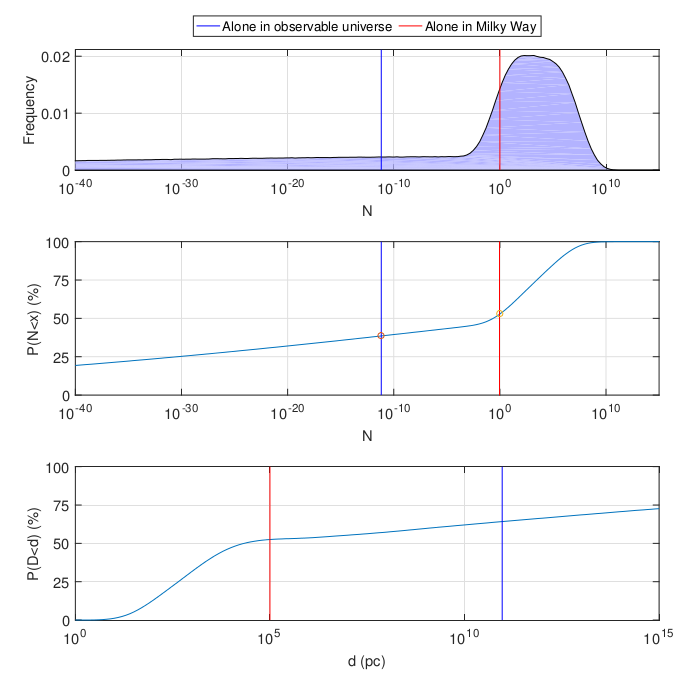
Anstatt Parameterschätzungen direkt aus der Literatur zu entnehmen, können Verteilungen konstruiert und analytisch berechnet werden. Ein Bereich von Schätzungen wird bis zu einer Größenordnung aufgenommen, und jeder Parameter wird als logarithmisch normal oder logarithmisch gleichmäßig im entsprechenden Intervall verteilt betrachtet. Das Ergebnis verschiebt sich etwas nach links, aber die Bedeutung ist dieselbe:



Was bedeutet das alles? Die richtige Antwort auf die Frage "Gibt es Leben im Universum oder ist es nicht da?" Immer noch "Ich weiß es nicht." Wie angenehm elegant die Bayes'sche Statistik ohne experimentelle Daten wenig kostet. Die Antwort auf die Frage „Wie sehr sollten wir uns über das Beobachtete wundern, hat sich geändert $$ "" Früher war es "Sehr stark, also ist entweder das Leben eine sehr seltene Sache, oder wir werden alle in einem Atomkrieg oder so etwas sterben ", und jetzt ist es "Nun, im Prinzip ist es nicht sehr wahrscheinlich, aber nichts Außergewöhnliches." Die Wahrscheinlichkeit eines Atomkrieges und / oder eines Treffens mit einem Dinosaurier gegen Newski- Außerirdische ist nur im Bayes'schen Sinne gesunken: Wir sind uns etwas weniger sicher, dass dies passieren wird. Ob diese Ereignisse tatsächlich eintreten oder nicht, hängt von den Faktoren der realen Welt ab (ungefähr Putin, Trump und Zorblaks, der galaktische Esser) und nicht von der Mathematik, mit der sie diskutiert werden.