Auto-Encoder und starke künstliche Intelligenz

Die Theorie der Auto-Encoder und Generierungsmodelle wurde kürzlich ernsthaft entwickelt, aber einige Arbeiten widmen sich der Verwendung bei Erkennungsproblemen. Gleichzeitig ermöglichen die Eigenschaft von Autoencodern, ein verstecktes parametrisches Datenmodell zu erhalten, und die daraus resultierenden mathematischen Konsequenzen, sie mit Bayes'schen Entscheidungsmethoden zu verknüpfen.

Der Artikel schlägt einen originalen mathematischen Apparat „eine Reihe von Auto-Encodern mit einem gemeinsamen latenten Raum“ vor, mit dem Sie abstrakte Konzepte aus den Eingabedaten extrahieren und die Fähigkeit zum „One-Shot-Lernen“ demonstrieren können. Darüber hinaus können damit viele der grundlegenden Probleme moderner Algorithmen für maschinelles Lernen überwunden werden, die auf mehrschichtigen Netzwerken und dem Ansatz des „Deep Learning“ basieren.

Hintergrund

Künstliche neuronale Netze, die unter Verwendung des Mechanismus der Rückausbreitung von Fehlern trainiert wurden, ersetzten fast viele Ansätze bei vielen Problemen der Erkennung und Parameterschätzung. Sie haben jedoch eine Reihe von Nachteilen, die anscheinend nicht ohne eine ernsthafte Überarbeitung des Ansatzes beseitigt werden können:

1. extreme Instabilität bei der Eingabe von Daten, die nicht in der Trainingsstichprobe enthalten sind (auch bei gegnerischen Angriffen)
   
   
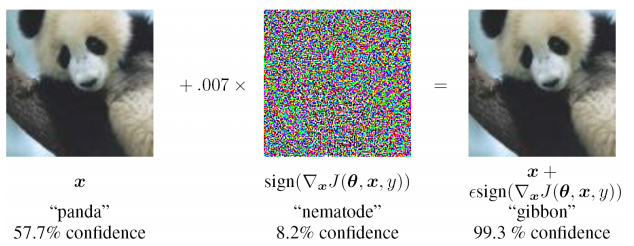
2. Es ist schwierig, die Ursache des Problems zu beurteilen und lokal auf einer der Ebenen neu zu trainieren (Sie müssen nur die Trainingsprobe ergänzen und neu trainieren), d. h. Black-Box-Problem
3. Die Möglichkeit unterschiedlicher Interpretationen derselben Eingabeinformationen wird nicht bereitgestellt, der statistische Charakter der beobachteten Daten wird ignoriert
   
   

Ich beschäftige mich mit der Lösung angewandter Probleme und stütze mich auf eine Reihe bestehender Arbeiten. Ich schlage einen Ansatz vor, der sich deutlich von den bestehenden unterscheidet, eine Reihe ihrer Mängel beseitigt und zur Lösung angewandter Probleme in verschiedenen Bereichen des maschinellen Lernens anwendbar ist.

Auto Encoder zur Schätzung der Verteilungsdichte

In der Theorie der Entscheidungsfindung nimmt die Verteilungsdichte (oder Verteilungsfunktion) von Zufallsvariablen einen sehr wichtigen Platz ein. Für die Berechnung des posterioren Risikos sind Schätzungen der Verteilungsfunktionen erforderlich.

Es stellt sich heraus, dass Auto-Encoder für die Bewertung von Verteilungsfunktionen sehr natürlich sind. Dies kann wie folgt erklärt werden: Der Trainingsdatensatz wird durch die Dichte ihrer Verteilung bestimmt. Je höher die Dichte der Trainingsbeispiele um einen lokalen Punkt im Eingaberaum ist, desto besser rekonstruiert der Auto-Encoder den Eingabevektor an dieser Stelle im Raum. Darüber hinaus gibt es im Autoencoder einen Vektor der latenten Darstellung der Eingabedaten (normalerweise von geringer Dimension). Wenn die Daten im latenten Raum in einen Bereich projiziert werden, der zuvor nicht im Training verwendet wurde, gab es in der Trainingsprobe nichts Ähnliches.

Es gibt eine Reihe von geschlossenen und etwas isolierten Werken:

1. Alain, G. und Bengio, Y. Was regulierte Autoencoder aus der Verteilung der Datengenerierung lernen. 2013.
2. Kamyshanska, H. 2013. Zur Autoencoder-Wertung
3. Daniel Jiwoong Im, Mohamed Ishmael Belghazi, Roland Memisevic. 2016. Konservativität von ungebundenen Auto-Encodern

Das erste rechtfertigt, dass das Ergebnis der Entrauschungsrekonstruktion von Auto-Encodern mit der Wahrscheinlichkeitsdichtefunktion der Eingabedaten zusammenhängt, aber Auto-Encodern eine Reihe von Einschränkungen auferlegt sind. Die zweite enthält ausreichende Anforderungen an den Auto-Encoder - die Encoder- und Decodergewichte müssen "verbunden" sein, d. H. Die Gewichtsmatrix der Codiererschicht ist die transponierte Matrix des Decodierers. In der letzten Arbeit werden die notwendigen und ausreichenden Bedingungen dafür, dass der Auto-Encoder mit einer Wahrscheinlichkeitsdichte verbunden ist, genauer untersucht.

Diese Arbeiten begründen streng die theoretische Grundlage für die Beziehung von Autoencodern zur Verteilungsdichte von Trainingsdaten. Bei angewandten Problemen ist eine derart schwerwiegende Analyse häufig nicht erforderlich. Daher wird im Folgenden ein etwas anderer Ansatz angegeben, mit dem wir die Wahrscheinlichkeitsdichtefunktion von Eingabedaten aufgrund eines zuvor trainierten Autoencoders abschätzen können.

MNIST-Beispiel

In noch früheren Arbeiten wurde die empirische Idee vorgeschlagen, dass es für das Klassifizierungsproblem möglich ist, Auto-Encoder nach der Anzahl der Klassen zu trainieren (wobei jeder von ihnen nur auf der entsprechenden Teilstichprobe unterrichtet wird). Und wählen Sie als Antwort die Klasse und den automatischen Encoder, die die minimale Diskrepanz zwischen dem Eingabebild und dem rekonstruierten Bild ergeben. Es war nicht schwierig, MNIST zu überprüfen: 10 Auto-Encoder (für jede Ziffer) zu trainieren, die Genauigkeit zu berechnen und dann mit einem ähnlichen Mehrschichtmodell des Klassifikators zu vergleichen.

Skripte zum Trainieren und Testen auf Git (train_ae.py, calc_codes.py, calc_acc.py)

Architektur und Anzahl der Gewichte:



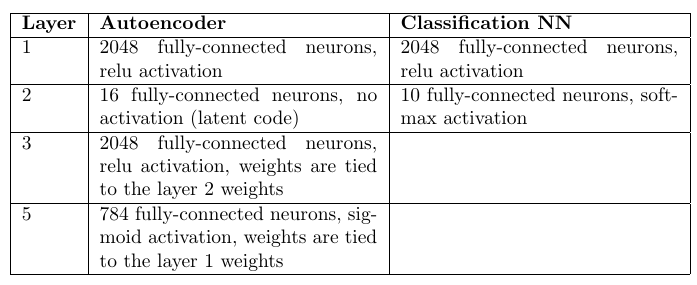
Auto Encoder: 98,6%
Mehrschichtiger Perzeptron-Klassifikator: 98,4%

Ein aufmerksamer Leser wird feststellen, dass Auto-Encoder 10-mal mehr Gewichte hatten (nach ihrer Anzahl). Eine 10-fache Erhöhung der Anzahl der Gewichte in der verborgenen Schicht in einem mehrschichtigen Perzeptron verschlechtert jedoch nur die Statistik.

Natürlich bieten Faltungsnetzwerke eine viel höhere Genauigkeit, aber die Aufgabe bestand nur darin, Ansätze zu vergleichen, wobei alle anderen Dinge gleich sind.

Infolgedessen kann festgestellt werden, dass der Ansatz mit Auto-Encodern mit vollständig verbundenen Netzwerken ziemlich wettbewerbsfähig ist. Und obwohl die Optimierung der Gewichte viel länger dauert, hat sie einen wichtigen Vorteil: die Fähigkeit, Anomalien in den Eingabedaten zu erkennen. Wenn nicht einer der Auto-Encoder das Eingabebild genau rekonstruieren konnte, können wir feststellen, dass ein anomales Bild eingegeben wurde, das im Trainingsmuster nicht aufgetreten ist. Genau genommen können Sie ein Bild nicht aus dem Eingabebeispiel rekonstruieren, aber was in dieser Situation zu tun ist, wird später gezeigt.

Betrachten Sie einen einzelnen Auto-Encoder

Es ist auf etwas andere Weise als in den obigen Veröffentlichungen möglich, eine qualitative Analyse der Beziehung zwischen der Wahrscheinlichkeitsdichte der Eingabedaten p (x) und der Antwort des Autoencoders durchzuführen.

Auto Encoder - sequentielle Verwendung der Encoderfunktion $$$z = g (x)$ und Decoder $$$x ^ * = f (z)$ wo $$$x$ Ist der Eingabevektor und $$$z$ - latente Leistung. In einigen Teilmengen von Eingaben (normalerweise in der Nähe des Trainings) $$$x ^ * = x + n = f (g (x))$ wo $$$n$ - Diskrepanz. Wir akzeptieren die Diskrepanz durch das Gausovsky-Rauschen (seine Parameter können nach dem Training des Autoencoders geschätzt werden). Infolgedessen wird eine Reihe ziemlich starker Annahmen getroffen:

1) Diskrepanz - Gaußsches Rauschen
2) Der Auto-Encoder ist bereits „trainiert“ und funktioniert

Wichtig ist jedoch, dass dem Auto-Encoder selbst fast keine Einschränkungen auferlegt werden.

Ferner kann eine qualitative Schätzung der Wahrscheinlichkeitsdichte p (x) erhalten werden, auf deren Grundlage mehrere Schlussfolgerungen gezogen werden können, die für die Zukunft sehr wichtig sind.

P (x) Punktzahl für einen einzelnen Auto-Encoder

Verteilungsdichte für $$$x \ in X$ und $$$z \ in Z$ wie folgt verwandt:

$$

$$p (x) = \ int_ {z} p (x | z) p (z) dz \; \; \; (1)$$

Wir müssen die Verbindung p (x) und p (z) erhalten. Bei einigen Auto-Encodern wird p (z) in der Phase ihres Trainings eingestellt, bei anderen ist p (z) aufgrund der kleineren Abmessung Z noch einfacher zu erhalten.

Die Dichteverteilung des Restes n ist bekannt, was bedeutet:

$$

$$p (n) = const \ times exp (- \ frac {(xf (z)) ^ T (xf (z))} {2 \ sigma ^ 2}) = p (x | z) \; \; 2)$$

$$$(x-f (z)) ^ T (x-f (z))$ Ist der Abstand zwischen x und seiner Projektion x *. Irgendwann z * erreicht dieser Abstand sein Minimum. An dieser Stelle sind die partiellen Ableitungen des Arguments des Exponenten in Formel (2) in Bezug auf $$$z_i$ (Z-Achse) ist Null:

$$

$$0 = \ frac {\ partielles f (z ^ *)} {\ partielles z_i} ^ T (xf (z ^ *)) + (xf (z ^ *)) ^ T \ frac {\ partielles f (z ^ * )} {\ partielle z_i}$$

Hier $$$\ frac {\ partielles f (z ^ *)} {\ partielles z_i} ^ T (x-f (z ^ *))$ Skalar dann:

$$

$$0 = \ frac {\ partielles f (z ^ *)} {\ partielles z_i} ^ T (x-f (z ^ *)) \; \; \; (3)$$

Die Wahl des Punktes z *, wo die Entfernung $$$(x-f (z)) ^ T (x-f (z))$ minimal aufgrund des Optimierungsprozesses des Auto-Encoders. Während des Trainings wird (in der Regel) der quadratische Rest minimiert: $$$\ min \ limitiert _ {\ theta, \ forall x \ in X train} L2_ {norm} ({x-f_ \ theta (g_ \ theta (x))})$ wo $$$\ theta$ - das Gewicht des Encoders. Das heißt, nach dem Training neigt g (x) zu z *.

Wir können auch expandieren $$$f (z)$ in einer Taylor-Reihe (bis zum ersten Term) um z *:

$$

$$f (z) = f (z ^ *) + \ nabla f (z ^ *) (z-z ^ *) + o ((z-z ^ *))$$

Nun wird Gleichung (2):

$$

$$p (x | z) \ ungefähr const \ times exp (- \ frac {((xf (z ^ *)) - \ nabla f (z ^ *) (zz ^ *)) ^ T ((xf (z ^) *)) - \ nabla f (z ^ *) (zz ^ *))} {2 \ sigma ^ 2}) =$$

$$

$$= const \ times exp (- \ frac {(xf (z ^ *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) exp (- \ frac {(\ nabla f (z ^ *) (zz ^ *)) ^ T (\ nabla f (z ^ *) (zz ^ *))} {2 \ sigma ^ 2}) \ times$$

$$

$$\ times exp (- \ frac {(\ nabla f (z ^ *)) ^ T (xf (z ^ *)) + (xf (z ^ *)) ^ T \ nabla f (z ^ *)) (zz ^ *)} {2 \ sigma ^ 2})$$

Beachten Sie, dass der letzte Faktor aufgrund von Ausdruck (3) 1 ist. Der erste Faktor kann durch das Vorzeichen des Integrals (es enthält kein z) in (1) entfernt werden. Und nehmen wir auch an, dass p (z) eine ausreichend glatte Funktion ist und sich in der Nachbarschaft von z * nicht viel ändert, d.h. Ersetzen Sie p (z) -> p (z *).

Nach allen Annahmen hat das Integral (1) die Schätzung:

$$

$$p (x) = const \ times p (z ^ *) exp (- \ frac {(xf (z ^ *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) \ int_ {z} exp (- (zz ^ *) ^ TW (x) ^ TW (x) (zz ^ *)) dz, \; \; \; z ^ * = g (x)$$

wo $$$W (x) = \ frac {\ nabla f (z ^ *)} {\ sigma}, z ^ * = g (x)$
Das letzte Integral ist das n-dimensionale Euler-Poisson-Integral:

$$

$$\ int_ {z} exp (- \ frac {(zz ^ *) ^ TW (x) ^ TW (x) (zz ^ *)} {2}) dz = \ sqrt {\ frac {1} {det ( W (x) ^ TW (x) / 2 \ pi)}}$$

Als Ergebnis haben wir die endgültige Schätzung p (x) erhalten:

$$

$$p (x) = const \ times exp (- \ frac {(xf (z ^ * *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) p (z ^ *) \ sqrt {\ frac {1} {det (W (x) ^ TW (x) / 2 \ pi)}}, z ^ * = g (x) \; \; \; (4)$$

All diese Mathematik wurde benötigt, um zu zeigen, dass p (x) von drei Faktoren abhängt:

• Je schlechter der Eingangsvektor und seine Rekonstruktion sind, desto kleiner ist p (x), je schlechter er wiederhergestellt wird.
• Wahrscheinlichkeitsdichten p (z *) bei z * = g (x)
• Normalisierung der Funktion p (z) am Punkt z *, die für den Autoencoder aus partiellen Ableitungen der Funktion f berechnet wird

Und aus der Normalisierungskonstante, die anschließend für die a priori-Wahrscheinlichkeit verantwortlich ist, einen Auto-Encoder zur Beschreibung der Eingangsdaten zu wählen.

Trotz aller Annahmen war das Ergebnis aus rechnerischer Sicht sehr aussagekräftig und nützlich.

Parameterklassifizierung oder Bewertungsverfahren

Jetzt können Sie das Klassifizierungsverfahren mit einer Reihe von Auto-Encodern genauer beschreiben:

1. Schulung unabhängiger Auto-Encoder für jede Klasse am entsprechenden Ausgang
2. Berechnung der Matrix W für jeden Autoencoder
3. P (z) Punktzahl für jeden automatischen Encoder

Und für jeden Eingabevektor können Sie jetzt auswerten $$$p (x | class)$ durch die Anzahl der Klassen. Und dies wird die Wahrscheinlichkeitsfunktion sein, die für die Entscheidungsfindung im Rahmen der Bayes'schen Entscheidungsregel erforderlich ist.

Auf die gleiche Weise können unbekannte Parameter auch geschätzt werden, indem der Parameterraum in diskrete Werte aufgeteilt wird, indem für jeden Wert ein eigener Auto-Encoder trainiert wird. Wählen Sie dann basierend auf der besten Bayes'schen Punktzahl den Wert aus, der die Maximum-Likelihood-Funktion ergibt.

Hier ist anzumerken, dass das Problem der Schätzung von p (z) formal nicht einfacher ist als die Schätzung von p (x). In der Praxis ist dies jedoch nicht der Fall. Der Raum Z hat normalerweise eine viel kleinere Abmessung, oder die Verteilung wird im Allgemeinen eingestellt, wenn die Gewichte des automatischen Codierers optimiert werden.

Die Idee, den latenten Raum von Auto-Encodern zu kombinieren

Es gibt eine merkwürdige Interpretation, die von Alexei Redozubov vorgeschlagen und in den folgenden Artikeln beschrieben wird:

1. Eine künstliche neuronale Netzwerkarchitektur basierend auf Kontexttransformationen in kortikalen Minisäulen. Vasily Morzhakov, Alexey Redozubov
2. Holographisches Gedächtnis: Ein neuartiges Modell der Informationsverarbeitung durch neuronale Mikroschaltungen. Alexey Redozubov, Springer
3. Überhaupt keine neuronalen Netze. Morzhakov V.

Informationen können in verschiedenen Kontexten völlig unterschiedlich interpretiert werden. Das Modell eines „Satzes von Auto-Encodern“ spiegelt diese vorgeschlagene Idee wider. Jeder automatische Codierer ist ein latentes Modell von Eingabedaten innerhalb desselben Kontexts (eine Klasse oder andere feste Parameter), d. H. Der latente Vektor ist eine Interpretation, und jeder Auto-Encoder ist ein Kontext. Beim Empfang von Eingabeinformationen werden diese in jedem Kontext (von jedem Auto-Encoder) berücksichtigt und der Kontext ausgewählt, der höchstwahrscheinlich vorhandene Modelle in jedem Auto-Encoder berücksichtigt.

Der nächste vernünftige Schritt besteht darin, die Überschneidung von Interpretationen in verschiedenen Kontexten zu ermöglichen. Das heißt, Während des Trainings wissen wir oft, dass die Interpretation gleich bleibt, aber die Form der Präsentation (Kontext) sich ändert. Beispielsweise ändert sich die Ausrichtung eines Objekts, das Objekt bleibt jedoch gleich. Der Vektor der Beschreibung des Objekts muss erhalten bleiben, und die Kontextorientierung ändert sich.

Wenn wir uns dann die Formel (4) ansehen, stellt sich heraus, dass der Faktor p (z) für den gesamten Satz von Auto-Encodern und nicht für jeden einzeln geschätzt wird. Die Interpretation (latenter Vektor) hat eine gemeinsame Verteilung. Für eine kleine Anzahl von Auto-Encodern spielt dies möglicherweise keine wesentliche Rolle, aber bei einer realen Aufgabe kann diese Anzahl sehr groß sein. Wenn Sie beispielsweise einen Kontext für jede mögliche Ausrichtung eines 3D-Objekts definieren, gibt es möglicherweise Hunderttausende davon. Nun bildet jedes Beispiel, das für das Training in einem beliebigen Kontext präsentiert wird, eine Verteilung p (z).

Austauschbarkeit von Interpretation und Kontext

Bei dem angewandten Problem stellt sich sofort die Frage: Was ist durch Interpretation und was durch Kontext zuzuweisen? Kontext und Interpretation können leicht ausgetauscht werden, und niemand schließt die Möglichkeit der gleichzeitigen parallelen Funktion eines Paares von "Autoencoder-Sätzen" aus.

Zur Verdeutlichung können Sie dieses Beispiel anbieten:

Das Eingabebild enthält die Gesichter von Personen.

1. Kontext - Gesichtsorientierung. Für die Rekonstruktion des Eingabebildes haben wir dann nicht genügend „Interpretation“ - einen Code, der eine Person identifiziert und eine Beschreibung des Gesichts, der Frisur und ihrer Beleuchtung enthält. Während des Trainings müssen wir dasselbe Gesicht von verschiedenen Seiten präsentieren, den latenten Code „einfrieren“ und gleichzeitig die Ausrichtung ändern.
2. Kontext - Art des Gesichts, Beleuchtung, Frisur. Für die Rekonstruktion des Eingabebildes fehlt dann die Ausrichtung des Gesichts. Während des Trainings müssen unterschiedliche Gesichter bei unterschiedlichen Lichtverhältnissen, jedoch mit derselben Ausrichtung gezeigt werden.

Die optimale Bayes'sche Entscheidung wird im ersten Fall hinsichtlich der Ausrichtung des Gesichts und im zweiten Fall hinsichtlich seines Typs getroffen. Vermutlich ergibt die erste Option eine bessere Orientierungsgenauigkeit, und die zweite Option bewertet genauer, wessen Gesicht es war.

Lernen einer Reihe von Auto-Encodern mit gemeinsamem latenten Raum

Im Training müssen wir wissen, wie eine Entität in Bezug auf die Bedeutung in verschiedenen Kontexten aussieht. Wenn wir zum Beispiel über das Bild von Zahlen und die Kontextorientierung sprechen, sieht ein solches Cross-Training schematisch so aus:



Der Codierer eines automatischen Codierers wird verwendet, dann wird der latente Code vom Decodierer eines anderen automatischen Codierers decodiert. Die Lernverlustfunktion bleibt Standard. Interessanterweise werden, wenn der Auto-Encoder symmetrisch ausgewählt ist (d. H. Die Gewichte des Codierers und des Decodierers sind verbunden), in jeder Iteration alle Gewichte beider Auto-Codierer optimiert.

Das bequemste für solch knifflige Schulungen war PyTorch, mit dem Sie ziemlich komplexe Schemata für die Rückübertragung von Fehlern erstellen können, einschließlich dynamischer.

Die Standard-Lernschritte jedes Auto-Encoders wechseln sich mit der Iteration des Cross-Trainings ab. Infolgedessen haben alle Auto-Encoder einen gemeinsamen latenten Raum oder eine „Interpretation“ in unterschiedlichen Kontexten.

Es ist sehr wichtig, dass wir als Ergebnis einer solchen Analyse die eingegebenen Informationen in „Kontext“ und „Interpretation“ unterteilen können.

Trainingsbeispiel

Stellen Sie sich ein ziemlich einfaches Beispiel vor, das auf MNIST basiert und das Prinzip des Trainings von Autoencodern mit einem gemeinsamen latenten Raum demonstriert. Infolgedessen wird in diesem Beispiel die Bildung des abstrakten Konzepts des „Würfels“ unter Verwendung des im Artikel beschriebenen Mechanismus demonstriert.

Die Zahlen von MNIST sind am Rand des Würfels aufgetragen und er dreht sich um eine seiner Achsen:



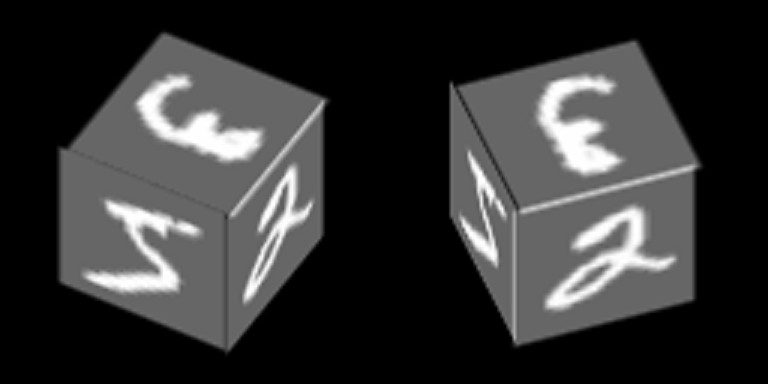
Wir werden Autoencoder trainieren, um Gesichter wiederherzustellen, Kontext - Gesichtsorientierung.

Hier ist ein Beispiel für die Zahl "Null" in 100 Kontexten, von denen die ersten 34 unterschiedlichen Drehwinkeln der Seitenfläche und die verbleibenden 76 - unterschiedlichen Drehwinkeln der Oberseite entsprechen.



Wir gehen davon aus, dass für jedes dieser 100 Bilder die „Interpretationen“ gleich sein sollten und es ihre zufälligen Kombinationen sind, die für das Cross-Training verwendet werden.

Nach dem Training mit dem oben beschriebenen Verfahren konnte erreicht werden, dass der latente Code eines der Autoencoder von anderen Autoencodern decodiert werden kann, wodurch eine wirklich aussagekräftige kontextbezogene Konvertierung erhalten wird.

Dieses Bild zeigt beispielsweise, wie das Codierungsergebnis des automatischen Codierers bei Nummer 10 von anderen automatischen Codierern für eine der Ziffern decodiert wird:



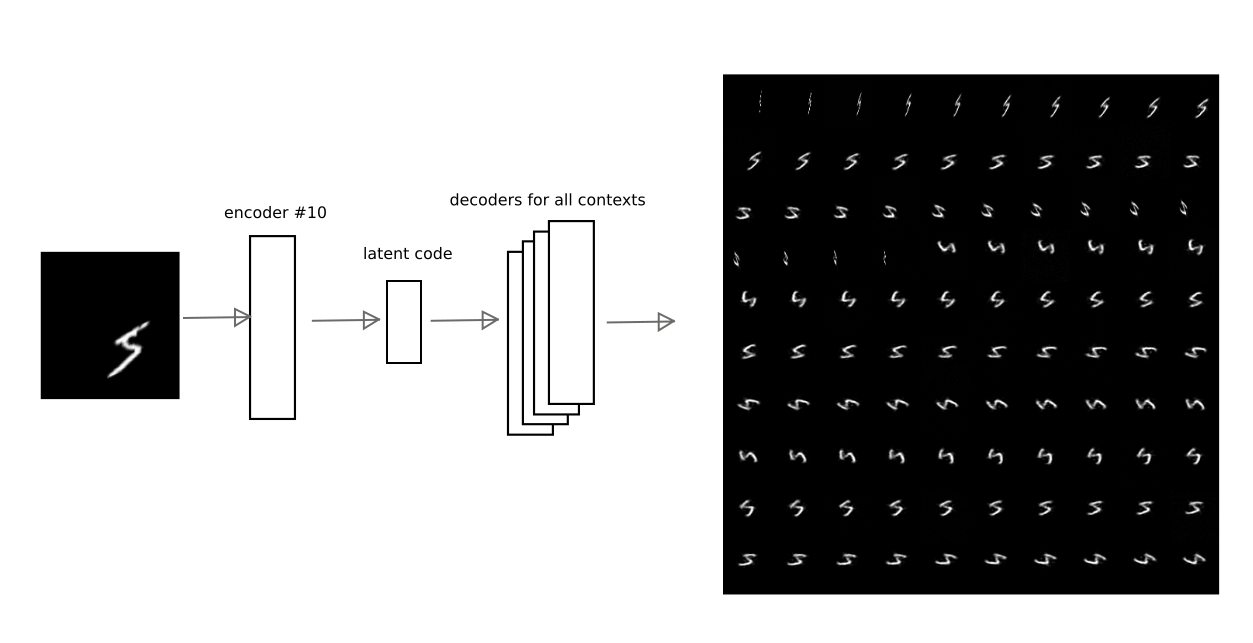
Somit kann der Code der "Interpretation", d.h. Latenter Vektor des Auto-Encoders, Sie können das Originalbild in jedem der trainierten Kontexte wiederherstellen (d. h. dem Decoder eines Auto-Encoders).

Eingabevektormaskierung

In Formel (4) ist die Dispersion des Restes $$$\ sigma$ , die durch eine Konstante für eine der Komponenten des Eingabevektors ausgewählt wird. Wenn jedoch einige Komponenten keine statistische Beziehung zum latenten Modell haben, ist die Varianz für diese Komponenten wahrscheinlich signifikant höher. Die Dispersion ist überall im Nenner, was bedeutet, dass der Beitrag des Komponentenfehlers umso geringer ist, je größer die Diskrepanz ist. Sie können dies als Maskierung eines Teils des Eingabevektors bezeichnen.

In diesem Beispiel mit rotierenden Gesichtern ist die Maske offensichtlich - die Projektion des Gesichts in einem bestimmten Kontext.



Bei dem vereinfachten Ansatz in diesem Beispiel, bei dem nur der Rest zwischen dem Eingabebild und der Rekonstruktion verwendet wird, müssen Sie nur den Rest mit der Maske für jeden der Kontexte multiplizieren.

Im allgemeinen Fall ist es notwendig, die Verteilungsparameter strenger auszuwerten, ohne die Maske manuell einzugeben.

Trennung von Interpretation und Kontext

Wenn Sie die Interpretation vom Kontext trennen, erhalten Sie abstrakte Konzepte. Im trainierten Beispiel ist es interessant, zwei Effekte zu demonstrieren:

1) einmaliges Lernen, d.h. Training mit einer extrem kleinen Anzahl von Beispielen (in der Grenze von einem).

Wenn wir nur die Interpretation analysieren und den Kontext ignorieren, wird es möglich, ein neues Bild in verschiedenen Gesichtsausrichtungen zu erkennen, wenn ein neues Bild nur in einer der Ausrichtungen gezeigt wurde.

Es ist wichtig zu beachten, dass ein neues Bild präsentiert werden muss. Aus Gründen der Korrektheit haben wir uns auch das Ziel gesetzt, uns nicht nur ein Bild zu merken, sondern zu lernen, wie man zwei neue Bilder teilt, die zuvor nicht in der MNIST-Trainingsbasis gefunden wurden. Zum Beispiel:



Die Idee ist wie folgt: Zeigen Sie diese Zeichen in einem der geometrischen Kontexte (z. B. unter Nummer 10), wählen Sie eine Hyperebene aus, die von den Interpretationen dieser Zeichen gleich weit entfernt ist, und stellen Sie dann sicher, dass wir mit dieser Hyperebene erkennen können, welche Art von Zeichen uns präsentiert wird, wenn das Gesicht gedreht wird (andere Kontexte).

Hierbei ist zu beachten, dass Auto-Encoder nicht auf neue Zeichen geschult werden. Aufgrund der Vielzahl von Zahlen in MNIST können Sie vorhersagen, wie ein neues Zeichen, das zuvor noch nicht gesehen wurde, in unterschiedlichen Kontexten aussehen wird.

Das V-Zeichen kümmert sich also um die Codierung im Kontext von Nr. 10 und die Decodierung in den übrigen:



Es ist ersichtlich, dass die Vorhersage nicht perfekt, aber visuell erkennbar ist.

Wir bezeichnen diese Demonstration als "Experiment 1" und beschreiben das Ergebnis unten.

2) und mit dem Würfel ist es interessant zu demonstrieren, was passieren wird, wenn Sie den Inhalt des latenten Vektors ignorieren und nur der Plausibilitätsgrad jedes Auto-Encoders übermittelt wird.

Lassen Sie uns sehen, wie die Wahrscheinlichkeit für jeden der Kontexte für zwei Würfel mit völlig unterschiedlichen Texturen (Nummern 5 und 9) für 100 Kontexte aussieht, die als Karte angezeigt werden können:



Es ist ersichtlich, dass die Karten trotz der unterschiedlichen Textur an den Seiten des Würfels ziemlich ähnlich sind.

Das heißt,Der Vektor selbst, der die Wahrscheinlichkeit von Autoencoder-Modellen (Kontexten) enthält, ermöglicht es uns, ein neues abstraktes Konzept zu formulieren, das sich auf die dreidimensionale Form eines Würfels bezieht. Dieser Vektor kann auch auf der nächsten Ebene durch einen Auto-Encoder beschrieben werden, der das Würfelmodell lernt.

Im zweiten Experiment muss eine zweite Ebene der Informationsverarbeitung erstellt werden, in der der Auto-Encoder eines abstrakten Würfelmodells trainiert wird. Verwenden Sie dann die Rückprojektion, um das Originalbild für verschiedene Implementierungen des Modells dieses Würfels wiederherzustellen. Einfach ausgedrückt, lassen Sie den Würfel drehen.

Das Ergebnis von "Experiment Nummer 1"

Der von MNIST geschulte Satz von Auto-Encodern gilt für zwei neue Bilder, die in Kontext 10 dargestellt werden. Es ergeben sich 2 Punkte im latenten Raum, die den Vorzeichen von V und + entsprechen. Wir definieren eine Ebene in gleichem Abstand von beiden Punkten, anhand derer wir eine Entscheidung treffen. Wenn sich der Punkt auf einer Seite der Ebene befindet - das V-Zeichen, auf der anderen - das Pluszeichen.

Jetzt erhalten wir die Codes der konvertierten Bilder und berechnen für jedes von ihnen den Abstand zur Ebene, wobei das Vorzeichen erhalten bleibt.

Dadurch kann unterschieden werden, welche Art von Zeichen für alle 100 Kontexte dargestellt wurde.

Entfernungsverteilung im Diagramm:



Visualisierung des Ergebnisses anhand einzelner Symbole als Beispiel:



Das heißt,Latente Codes von V-Zeichen in völlig unterschiedlichen Kontexten sind im latenten Raum viel näher beieinander als V- und Pluszeichencodes im selben Kontext. Aufgrund dessen ist es in 100 von 100 Fällen möglich, Zeichen in verschiedenen Ausrichtungen der Würfelflächen erfolgreich zu unterscheiden, obwohl nur eine Probe jedes Zeichens präsentiert wurde.

Es war möglich, das klassische „One-Shot-Lernen“ zu demonstrieren, das in der ursprünglichen Architektur künstlicher neuronaler Netze unmöglich ist. Das Grundprinzip, nach dem dieser Ansatz funktioniert, ist dem beispielsweise in diesem Artikel gezeigten „Transferlernen“ sehr ähnlich .

Link zu git (train_ae_shared.py, test_AB.py)

Das Ergebnis von "Experiment Nummer 2"

Das Trennen von Interpretationen vom Kontext ermöglicht auch das Lernen aus einer begrenzten Anzahl von Beispielen. Es ist möglich, nur eine der möglichen Interpretationen in verschiedenen Kontexten zu demonstrieren (Festlegen eines "latenten Vektors"). Ein abstraktes Würfelmodell kann erhalten werden, indem nur eine Ziffer auf allen Flächen angezeigt wird.

Das Experiment ist wie folgt aufgebaut:

1. Eine Trainingsbasis wird vorbereitet: Würfel mit einem Rotationsgrad von 0 bis 90 Grad. Auf den Flächen der Würfel steht die Nummer 5.
2. Der von der Interpretation getrennte Wahrscheinlichkeitsvektor von Kontexten (latenter Code) wird an die nächste Ebene übergeben, wo der für das Würfelmodell verantwortliche Auto-Encoder trainiert wird
3. : , «», , , , , .

Das Trainingsmuster bestand aus 5421 Bildern mit dem Bild der Nummer 5 an den Seiten, Beispiel:


Würfel mit einer Drehung von 0 bis 90 Grad.

Wir wissen im Voraus, dass der Würfel nur einen Rotationsfreiheitsgrad hat, daher hat der Auto-Encoder auf der zweiten Ebene nur eine Komponente im latenten Code. Nach dem Training können Sie diese Komponente von 0 bis 1 variieren (die Sigmoidfunktion wurde ausgewählt, um die latente Schicht zu aktivieren) und sehen, welcher Kontextwahrscheinlichkeitsvektor während der Decodierung reproduziert wird:



Dann wird dieser Vektor auf Ebene 1 übertragen, in der 100 Orientierungskontexte der Gesichter, lokalen Maxima und « stellte sich einen latenten Code des Zeichens auf den Flächen des Würfels vor. Stellen Sie sich die Nummer 3 auf den Gesichtern vor, ändern Sie den latenten Vektor im Auto-Encoder, der für das abstrakte Konzept eines Würfels verantwortlich ist, und erhalten Sie das folgende Bild eines Würfels:



Oder der Code des V-Zeichens, der im Trainingssatz überhaupt nicht vorkam:



Die Qualität ist schlechter, aber das Zeichen ist erkennbar.

Auf der zweiten Ebene der Bildverarbeitung haben wir einen automatischen Encoder erhalten, der die Vielfalt des abstrakten Konzepts des „Würfels“ modelliert. In der Praxis ist bei Erkennungsproblemen das im Experiment gezeigte Prinzip der Rückprojektion äußerst wichtig, weil ermöglicht es, die Mehrdeutigkeiten der Interpretation aufgrund der Bildung abstrakter Konzepte einer höheren Ebene zu beseitigen.

Link zu git (second_level.py, second_level_test.py)

Andere Beispiele, bei denen die Kontexttrennung funktioniert

In meinem vorherigen Artikel wurde beim Erkennen von Fahrzeugnummern eine ähnliche Methode ohne Erklärung verwendet. Die Position, Ausrichtung und Skalierung der Zahlen im Bild wurden vom Inhalt getrennt, die nächste Ebene nahm diese Daten wahr, um das Modell „Autonummer“ zu erstellen. Egal welche Zahlen, ihre gegenseitige geometrische Konfiguration ist wichtig, damit wir sicher sagen können, dass dies eine Autonummer ist (übrigens auch ein abstraktes Konzept).

In Analogie können wir eine Reihe anderer Beispiele aus der Bildverarbeitung nennen: Die 3D-Form eines Objekts oder seine Konturen sind von seiner Textur und seinem Hintergrund trennbar; Die Aufzählung der Komponenten isoliert von der gegenseitigen räumlichen Konfiguration ermöglicht häufig auch die Bildung eines neuen abstrakten Konzepts.

, : — ( ) ( ); ( , ,«- -»).

Im Moment ist es schwierig zu formulieren, wie sich die starke KI von der schwachen unterscheidet. Wahrscheinlich sollte diese Liste alles enthalten, was in bestehenden Ansätzen und Algorithmen fehlt, damit Computer so effizient wie eine Person agieren können, zum Beispiel:

• Entscheidungen treffen, Strategien anwenden, angesichts von Unsicherheiten lösen. Es ist eine hohe Unsicherheit, die die Auswahl der besten Modelle erfordert, die während des Trainings formuliert wurden
• Reflexion von Modellen der umgebenden physischen und sozialen Welt, einschließlich Selbstbewusstsein und Bewusstsein anderer
• Die Mechanismen des abstrakten Denkens, die es ermöglichen, Konzepte zu formulieren, die anschließend für eine Vielzahl von Eingabedaten verwendet werden können
• Fähigkeit, eigene Gedanken zu "entschlüsseln"

Es gibt auch eindeutig nicht genügend entwickelte Gedächtnismechanismen, die in den Lernprozess integriert sind, Beförderungs- / Bestrafungsmechanismen.

Der Artikel demonstriert die Herangehensweise an das Problem der Erkennung und Schätzung von Parametern, die auf der Auswahl des besten Modells basiert, das die Eingabedaten beschreibt. Es wird angenommen, dass dies der Mechanismus zur Auswahl der besten Interpretation und des besten Kontexts ist. Aufgrund der Trennung von Interpretation und Kontext am Ausgang des Moduls (einer Reihe von Auto-Encodern) kann man abstrakte Konzepte formulieren oder Erfahrungen isoliert vom Kontext verallgemeinern, wodurch die Trainingsstichprobe reduziert wird. Kontextsätze können die Messwerte von Maschinensensoren (Ausrichtung, Position, Geschwindigkeit usw.) widerspiegeln, wodurch natürliches Lernen ohne Lehrer möglich wird.

Obwohl Deep Learning beim Training von Autoencodern verwendet wird, können die in Autoencodern auftretenden Prozesse auf jeder Ebene der Informationsverarbeitung leicht analysiert werden, weil Es ist möglich zu bestimmen, in welchem ​​Modell (oder in welchem ​​Kontext) die beste Interpretation gefunden wurde. Die Bedeutung der Rückkopplungen zwischen den Ebenen, die in komplexen Systemen eingeführt werden müssen, besteht darin, die Wahrscheinlichkeit der Auswahl eines bestimmten Kontexts zu erhöhen oder zu verringern.

Ergebnis

Es wird ein mathematischer Apparat vorgeschlagen, auf dessen Grundlage man das eine oder andere Modell auswählen kann, das die Eingabedaten beschreibt, das von der Bayes'schen Entscheidungsregel geleitet wird. Modelle werden unter Verwendung von Autoencodern mit einem gemeinsamen latenten Raum erhalten. Es wird eine Idee vorgeschlagen, nach der der latente Code des Auto-Encoders eine Interpretation ist, und das latente Modell, d.h. Der Auto-Encoder selbst ist Kontext.

Am Beispiel von MNIST wird gezeigt, dass der Satz von Auto-Encodern hinsichtlich der Genauigkeit vollständig verbundenen künstlichen neuronalen Netzen nicht unterlegen ist.

Der Effekt der Trennung von Interpretation und Kontext wird gezeigt: Minimierung des erforderlichen Datensatzes (in der „One-Shot-Learning“ -Limit) für die Erkennung neu präsentierter Bilder aufgrund des Vortrainings mit anderen Daten.

Der Effekt der Trennung von Kontext und Interpretation wird gezeigt: Die Möglichkeit, abstrakte Konzepte der nächsten Ebene am Beispiel der geometrischen Abstraktion „Würfel“ zu bilden.

Referenzen

1) Alain, G. und Bengio, Y. Was regulierte Autoencoder aus der Verteilung der Datengenerierung lernen. 2013.
2) Kamyshanska, H. 2013. Zur Autoencoder-Wertung
3) Daniel Jiwoong Im, Mohamed Ishmael Belghazi, Roland Memisevic. 2016. Konservativität von ungebundenen Auto-Encodern
4) Eine künstliche neuronale Netzwerkarchitektur basierend auf Kontexttransformationen in kortikalen Minisäulen. Vasily Morzhakov, Alexey Redozubov
5) Holographisches Gedächtnis: Ein neuartiges Modell der Informationsverarbeitung durch neuronale Mikroschaltungen. Alexey Redozubov, Springer
6) Überhaupt keine neuronalen Netze. Morzhakov V.
7) en.wikipedia.org/wiki/Gaussian_integral
8) Widersprüchliche Beispiele: Angriffe und Abwehrkräfte für tiefes Lernen
9) One-Shot-Imitationslernen

PS: Dieser Artikel ist ein elektronischer Preprint in russischer Sprache, der veröffentlicht wurde, um die Ergebnisse zu diskutieren und nach Fehlern zu suchen. Jede konstruktive Kritik ist willkommen!