Einführung
Vor einiger Zeit nahm ich an einem Projekt zur Entwicklung eines Softwareprodukts teil, mit dem Patientenakten und Daten über ihren Gesundheitszustand von medizinischen Organisationen analysiert werden können, um eine einheitliche Krankenakte zu erstellen. Lange Zeit konnte das Team keinen Ansatz zur Kombination von Patientendaten entwickeln. Ausgangspunkt war die Untersuchung der Quellcodes der Open EMPI-Lösung (Open Enterprise Master Patient Index), die uns dazu veranlasste, Algorithmen zur Analyse der Ähnlichkeit zu verfolgen . Von diesem Moment an begann eine eingehendere Untersuchung der Materialien, die es ermöglichte, zuerst ein Layout und dann eine funktionierende Lösung zu erstellen.
Bisher muss man bei verschiedenen Arten von Präsentationen viele Fragen zur Logik der Arbeit solcher Produkte hören, aus denen ich schließe, dass eine Überprüfung der Textverknüpfungsmethoden für einen breiten Leserkreis von Interesse sein wird.
Das Material ist eine Übersetzung des Wikipedia-Artikels " Record Linkage " mit Copyright und Ergänzungen.
Was ist Textverknüpfung?
Der Begriff „ Datensatzverknüpfung“ beschreibt den Prozess des Anhängens von Textdatensätzen aus einer Datenquelle an Datensätze aus einer anderen, sofern diese dasselbe Objekt beschreiben. In der Informatik wird dies als "Datenabbildung" oder "Objektidentitätsproblem" bezeichnet . Manchmal werden alternative Definitionen verwendet, wie "Identifizierung" , "Bindung" , "Duplikaterkennung" , "Deduplizierung" , "Übereinstimmende Datensätze" , "Objektidentifizierung" , die dasselbe Konzept beschreiben. Diese terminologische Fülle hat zu einer Trennung von Informationsverarbeitungs- und Strukturierungsansätzen geführt - Datensatzbindung und Datenbindung . Obwohl beide die Identifizierung übereinstimmender Objekte durch unterschiedliche Parametersätze bestimmen, wird der Begriff "Verknüpfen von Textdatensätzen" häufig verwendet, wenn auf das "Wesen" einer Person Bezug genommen wird, während "Datenverknüpfung" die Möglichkeit bedeutet, eine Webressource zwischen Datensätzen zu verknüpfen. unter Verwendung des breiteren Konzepts eines Bezeichners, nämlich eines URI.
Warum wird das benötigt?
Bei der Entwicklung von Softwareprodukten zum Aufbau automatisierter Systeme, die in verschiedenen Bereichen im Zusammenhang mit der Verarbeitung personenbezogener Daten einer Person (Gesundheitswesen, Geschichte, Statistik, Bildung usw.) verwendet werden, besteht die Aufgabe darin, Daten zu Rechnungslegungsgegenständen aus verschiedenen Quellen zu identifizieren.
Beim Sammeln von Beschreibungen aus einer Vielzahl von Quellen treten jedoch Probleme auf, die ihre eindeutige Identifizierung erschweren. Diese Probleme umfassen:
- Tippfehler;
- Feldpermutationen (zum Beispiel im Vornamen);
- die Verwendung von Abkürzungen und Abkürzungen;
- die Verwendung eines anderen Formats von Kennungen (Datumsangaben, Dokumentennummern usw.).
- phonetische Verzerrung;
- usw.
Die Qualität der Rohdaten wirkt sich direkt auf das Ergebnis des Bindungsprozesses aus. Aufgrund dieser Probleme werden Datensätze häufig in die Verarbeitung übertragen, die, obwohl sie dasselbe Objekt beschreiben, so aussehen, als ob diese Datensätze unterschiedlich aussehen. Daher werden einerseits alle übertragenen Datensatzkennungen auf ihre Anwendbarkeit für den Identifizierungsprozess bewertet, und andererseits werden die Datensätze selbst normalisiert oder standardisiert, um sie in ein einziges Format zu bringen.
Geschichtstour
Die ursprüngliche Idee, Notizen zu verknüpfen, wurde von Halbert L. Dunn vorgebracht, der 1946 im American Journal of Public Health einen Artikel mit dem Titel „Record Linkage“ veröffentlichte.
Später, 1959, legte Howard B. Newcombe in einem Artikel über die automatische Verknüpfung lebenswichtiger Aufzeichnungen in der Zeitschrift Science die probabilistischen Grundlagen der modernen String-Bindungstheorie, die 1969 von Ivan Fellegi und Alan entwickelt und verstärkt wurden Santer (Alan Sunter). Ihre Arbeit „A Theory For Record Linkage“ ist immer noch die mathematische Grundlage für viele Verknüpfungsalgorithmen.
Die Hauptentwicklung der Algorithmen erfolgte in den 90er Jahren des letzten Jahrhunderts. Aus verschiedenen Bereichen (Statistik, Archivierung, Epidemiologie, Geschichte usw.) kamen dann Algorithmen zu uns, die heute häufig in Softwareprodukten verwendet werden, wie beispielsweise die Jaro-Winkler-Entfernung (Entfernung) und die Levenshtein- Entfernung. Einige Lösungen, zum Beispiel der phonetische Soundex-Algorithmus, erschienen jedoch viel früher - in den 20er Jahren des letzten Jahrhunderts.
Algorithmen für den Vergleich von Texteingaben
Unterscheiden Sie zwischen deterministischen und probabilistischen Algorithmen zum Vergleichen von Textdatensätzen. Deterministische Algorithmen basieren auf der vollständigen Übereinstimmung von Datensatzattributen. Probabilistische Algorithmen ermöglichen es, den Übereinstimmungsgrad von Datensatzattributen zu berechnen und auf dieser Grundlage über die Möglichkeit ihrer Beziehung zu entscheiden.
Deterministische Algorithmen
Der einfachste Weg, Zeichenfolgen zu vergleichen, basiert auf klaren Regeln, wenn Verknüpfungen zwischen Objekten basierend auf der Anzahl der Übereinstimmungen der Attribute der Datensätze generiert werden. Das heißt, zwei Datensätze entsprechen einander durch einen deterministischen Algorithmus, wenn alle oder einige ihrer Attribute identisch sind. Deterministische Algorithmen eignen sich zum Vergleichen von Personen, die durch eine Reihe von Daten beschrieben werden, die durch eine gemeinsame Kennung (z. B. die Versicherungsnummer eines einzelnen persönlichen Kontos in der Pensionskasse - SNILS) gekennzeichnet sind oder über mehrere repräsentative Kennungen (Geburtsdatum, Geschlecht usw.) verfügen, denen vertraut werden kann.
Deterministische Algorithmen können angewendet werden, wenn klar strukturierte (standardisierte) Datensätze in die Verarbeitung übertragen werden.
Zum Beispiel hat es die folgenden Texteingaben:
| Nein, nein. | SNILS | Vorname | Geburtsdatum | Geschlecht |
|---|
| A1 | 163-648-564 96 | Zhvanetsky Mikhail | 03/06/1934 | M. |
| A2 | 163-648-564 96 | Zhvanetsky Mikhail | 03/06/1934 | M. |
| A3 | 126-029-036 24 | Ilchenko Victor | 01/02/1937 | M. |
| A4 | | Novikova Klara | 26.12.1946 | F. |
| Nein, nein. | SNILS | Vorname | Geburtsdatum | Geschlecht |
|---|
| B1 | 126-029-036 24 | Ilyichenko Victor | 01/02/1937 | M. |
| B2 | | Zhivanetsky Mikhail | 03/06/1934 | M. |
| B3 | | Zerchaninova Klara | 26.12.1946 | 2 |
Es wurde zuvor gesagt, dass der einfachste deterministische Algorithmus die Verwendung einer eindeutigen Kennung ist, die eine Person eindeutig identifizieren soll. Beispielsweise nehmen wir an, dass alle Datensätze mit demselben Bezeichnerwert (SNILS) dasselbe Thema beschreiben, andernfalls handelt es sich um unterschiedliche Themen. Die deterministische Verbindung erzeugt in diesem Fall die folgenden Paare: A1 und A2, A3 und B1. B2 wird nicht mit A1 und A2 verknüpft, da die Kennung keine Rolle spielt, obwohl sie inhaltlich mit den angegebenen Datensätzen übereinstimmt.
Diese Ausnahmen führen dazu, dass der deterministische Algorithmus durch neue Regeln ergänzt werden muss. Wenn beispielsweise keine eindeutige Kennung vorhanden ist, können Sie andere Attribute wie Name, Geburtsdatum und Geschlecht verwenden. In dem gegebenen Beispiel ergibt diese zusätzliche Regel wiederum keine B2- und A1 / A2-Entsprechung, da die Namen jetzt unterschiedlich sind - es gibt eine phonetische Verzerrung des Nachnamens.
Dieses Problem kann mit den Methoden der phonetischen Analyse gelöst werden. Wenn Sie jedoch den Nachnamen ändern (z. B. im Falle einer Heirat), müssen Sie auf die Anwendung einer neuen Regel zurückgreifen, z. B. das Geburtsdatum vergleichen oder Unterschiede in den vorhandenen Attributen des Datensatzes zulassen (z. B. Geschlecht).
Das Beispiel zeigt deutlich, dass der deterministische Algorithmus sehr empfindlich auf die Datenqualität reagiert und eine Erhöhung der Anzahl der Datensatzattribute zu einer erheblichen Erhöhung der Anzahl der angewendeten Regeln führen kann, was die Verwendung deterministischer Algorithmen erheblich erschwert.
Darüber hinaus ist die Verwendung deterministischer Algorithmen möglich, wenn ein verifizierter Datensatz (Hauptreferenz) vorhanden ist, mit dem die eingehenden Informationen verglichen werden. Im Falle einer ständigen Auffüllung des Hauptverzeichnisses selbst kann jedoch eine vollständige Überarbeitung bestehender Beziehungen erforderlich sein, was die Verwendung deterministischer Algorithmen zeitaufwändig oder einfach unmöglich macht.
Probabilistische Algorithmen
Probabilistische Algorithmen zum Verknüpfen von Zeichenfolgendatensätzen verwenden einen größeren Satz von Attributen als deterministische, und für jedes Attribut wird ein Gewichtskoeffizient berechnet, der die Fähigkeit bestimmt, die Verbindung bei der endgültigen Bewertung der Wahrscheinlichkeit der Konformität geschätzter Datensätze zu beeinflussen. Datensätze, bei denen das Gesamtgewicht über einem bestimmten Schwellenwert angesammelt wurde, werden als verwandt betrachtet. Datensätze, bei denen das Gesamtgewicht unter einem bestimmten Schwellenwert angesammelt wurde, gelten als nicht verwandt. Paare, die den Wert des Gesamtgewichts aus der Mitte des Bereichs gewonnen haben, gelten als Kandidaten für die Verknüpfung und können später (z. B. vom Bediener) in Betracht gezogen werden, die über ihre Vereinigung (Verknüpfung) entscheiden oder sie ungebunden lassen. Im Gegensatz zu deterministischen Algorithmen, bei denen es sich um einen Satz einer großen Anzahl klarer (programmierter) Regeln handelt, können probabilistische Algorithmen daher durch Auswahl von Schwellenwerten an die Qualität der Daten angepasst werden und erfordern keine Neuprogrammierung.
Probabilistische Algorithmen weisen den Attributen des Datensatzes also Gewichtskoeffizienten ( u und m ) zu, mit deren Hilfe ihre Entsprechung oder Inkonsistenz untereinander bestimmt wird.
Der Koeffizient u bestimmt die Wahrscheinlichkeit, dass die Kennungen zweier unabhängiger Datensätze zufällig zusammenfallen. Zum Beispiel beträgt die U-Wahrscheinlichkeit des Geburtsmonats (wenn es zwölf gleichmäßig verteilte Werte gibt) 1 \ 12 = 0,083. Bezeichner mit Werten, die nicht gleichmäßig verteilt sind, haben unterschiedliche Wahrscheinlichkeiten für unterschiedliche Werte (manchmal einschließlich fehlender Werte).
Der Koeffizient m ist die Wahrscheinlichkeit, dass die Identifikatoren in den verglichenen Paaren einander entsprechen oder ziemlich ähnlich sind - zum Beispiel im Fall einer hohen Wahrscheinlichkeit durch den Jaro-Winkler-Algorithmus oder einer niedrigen Wahrscheinlichkeit durch den Levenshtein-Algorithmus. Wenn die Attribute der Datensätze vollständig konsistent sind, sollte dieser Wert einen Wert von 1,0 haben. Angesichts der geringen Wahrscheinlichkeit sollte der Koeffizient jedoch anders bewertet werden. Diese Bewertung kann auf der Grundlage einer vorläufigen Analyse des Datensatzes erfolgen, indem beispielsweise der Wahrscheinlichkeitsalgorithmus zum Identifizieren einer großen Anzahl von übereinstimmenden und nicht übereinstimmenden Paaren manuell "gelernt" wird oder indem der Algorithmus iterativ gestartet wird, um den am besten geeigneten m-Koeffizientenwert auszuwählen.
Wenn die m-Wahrscheinlichkeit als 0,95 definiert ist, sehen die Konformitäts- / Nichtkonformitätskoeffizienten für den Geburtsmonat folgendermaßen aus:
| Metrisch | Teilen von Links | Anteil von Werten, keine Referenzen | Frequenz | Gewicht |
|---|
| Compliance | m = 0,95 | u = 0,083 | m \ u = 11,4 | ln (m / u) / ln (2) ≤ 3,51 |
| Nichtübereinstimmung | 1 m = 0,05 | 1-u = 0,917 | (1-m) / (1-u) ≤ 0,0545 | ln ((1-m) / (1-u)) / ln (2) ≤ -4,20 |
Ähnliche Berechnungen sollten für andere Datensatzkennungen durchgeführt werden, um deren Konformitäts- und Nichtkonformitätskoeffizienten zu bestimmen. Dann wird jede Kennung eines Datensatzes mit der entsprechenden Kennung eines anderen Datensatzes verglichen, um das Gesamtgewicht des Paares zu bestimmen: Das Gewicht des entsprechenden Paares wird mit einer kumulierten Summe zum Gesamtergebnis addiert, während das Gewicht des unangemessenen Paares vom Gesamtergebnis abgezogen wird. Der resultierende Betrag wird mit den identifizierten Schwellenwerten verglichen, um zu bestimmen, ob das analysierte Paar automatisch gepaart oder zur Prüfung an den Bediener übertragen werden soll.
Blockieren
Die Bestimmung von Konformitäts- / Nichtkonformitätsschwellen ist ein Gleichgewicht zwischen dem Erhalten einer akzeptablen Empfindlichkeit (dem Anteil verwandter Datensätze, die vom Algorithmus erfasst werden) und dem Vorhersagewert des Ergebnisses (d. H. Genauigkeit als Maß für wirklich übereinstimmende Datensätze, die durch den Algorithmus verknüpft sind). Da das Definieren von Schwellenwerten eine sehr schwierige Aufgabe sein kann, insbesondere für große Datenmengen, wird häufig ein als Blockieren bekanntes Verfahren verwendet, um die Recheneffizienz zu erhöhen. Es wird versucht, einen Vergleich zwischen Datensätzen durchzuführen, bei denen eine signifikante Diskrepanz ( Diskriminierung ) in den Werten der Basisattribute festgestellt wird. Dies führt zu einer Erhöhung der Genauigkeit aufgrund einer Verringerung der Empfindlichkeit.
Zum Beispiel reduziert das Sperren basierend auf der phonetischen Codierung eines Nachnamens die Gesamtzahl der erforderlichen Vergleiche und erhöht die Wahrscheinlichkeit, dass die Beziehungen zwischen den Datensätzen korrekt sind, da die beiden Attribute bereits konsistent sind, aber möglicherweise Datensätze überspringen können, die sich auf dieselbe Person beziehen, deren Nachname geändert (zum Beispiel infolge der Ehe). Das Blockieren nach Geburtsmonat ist ein stabilerer Indikator, der nur angepasst werden kann, wenn die Quelldaten fehlerhaft sind, aber einen geringeren Vorteil hinsichtlich des positiven Vorhersagewerts und des Empfindlichkeitsverlusts bietet, da zwölf verschiedene Gruppen extrem großer Datenmengen erstellt werden und dies nicht zu einer Geschwindigkeitssteigerung führt Computing.
Daher verwenden die effizientesten Verknüpfungssysteme für Texteingaben häufig mehrere Blockierungsdurchläufe, um Daten auf verschiedene Weise zu gruppieren, um Gruppen von Datensätzen vorzubereiten, die später zur Analyse eingereicht werden sollten.
Maschinelles Lernen
In letzter Zeit wurden verschiedene Methoden des maschinellen Lernens verwendet, um Textdatensätze zu verknüpfen. Randall Wilson hat in seiner Arbeit von 2011 gezeigt, dass der klassische probabilistische Verknüpfungsalgorithmus für Textdatensätze dem naiven Bayes-Algorithmus entspricht und unter der Annahme, dass Klassifizierungsmerkmale unabhängig sind, dieselben Probleme hat. Um die Genauigkeit der Analyse zu erhöhen, schlägt der Autor vor, ein Grundmodell eines neuronalen Netzwerks zu verwenden, das als einschichtiges Perzeptron bezeichnet wird und dessen Verwendung es ermöglicht, die mit herkömmlichen probabilistischen Algorithmen erzielten Ergebnisse signifikant zu übertreffen.
Phonetische Codierung
Phonetische Algorithmen stimmen mit zwei ähnlich ausgesprochenen Wörtern mit denselben Codes überein, sodass Sie solche Wörter anhand ihrer phonetischen Ähnlichkeit vergleichen können.
Die meisten phonetischen Algorithmen dienen zur Analyse englischer Wörter, obwohl kürzlich einige Algorithmen für die Verwendung mit anderen Sprachen modifiziert wurden oder ursprünglich als nationale Lösungen erstellt wurden (z. B. Caverphone).
Soundex
Der klassische Algorithmus zum Vergleichen von zwei Saiten nach ihrem Klang ist Soundex (kurz für Klangindex). Es wird der gleiche Code für Zeichenfolgen festgelegt, die auf Englisch einen ähnlichen Klang haben. Soundex wurde ursprünglich in den 1930er Jahren von der US National Archives Administration verwendet, um Volkszählungen von 1890 bis 1920 nachträglich zu analysieren.
Die Autoren der Algorithmen sind Robert C. Russel und Margaret King Odell, die sie in den 20er Jahren des letzten Jahrhunderts patentierten. Der Algorithmus selbst gewann in der zweiten Hälfte des letzten Jahrhunderts an Popularität, als er Gegenstand mehrerer Artikel in populärwissenschaftlichen Fachzeitschriften in den USA wurde und in D. Knuts Monographie „The Art of Programming“ veröffentlicht wurde.
Daitch-Mokotoff Soundex
Da Soundex nur für Englisch geeignet ist, haben einige Forscher versucht, es zu ändern. 1985 schlugen Gary Mokotoff und Randy Daitch eine Variante des Soundex-Algorithmus vor, mit der osteuropäische (einschließlich russischer) Nachnamen mit einer relativ hohen Qualität verglichen werden sollen.
In den 90er Jahren schlug Lawrence Philips (Lawrence Philips) eine alternative Version des Soundex-Algorithmus vor, der als Metaphone bezeichnet wurde. Der neue Algorithmus verwendete ein größeres Regelwerk für die englische Aussprache, aufgrund dessen es genauer war. Später wurde der Algorithmus geändert, um in anderen Sprachen verwendet zu werden, basierend auf der Transkription unter Verwendung von Buchstaben des lateinischen Alphabets.
Im Jahr 2002 veröffentlichte die 8. Ausgabe des Programmer-Magazins einen Artikel von Peter Kankowski über seine Anpassung der englischen Version des Metaphone-Algorithmus. Diese Version des Algorithmus konvertiert die Quellwörter gemäß den Regeln und Normen der russischen Sprache, wobei der phonetische Klang nicht betonter Vokale und die mögliche "Verschmelzung" von Konsonanten in der Aussprache berücksichtigt werden.
Anstelle einer Schlussfolgerung
Infolge mehrerer Iterationen entwickelte das in der Einleitung erwähnte Projektteam des Softwareproduktentwicklungsprojekts eine Architekturlösung, deren Schema in der Abbildung dargestellt ist.
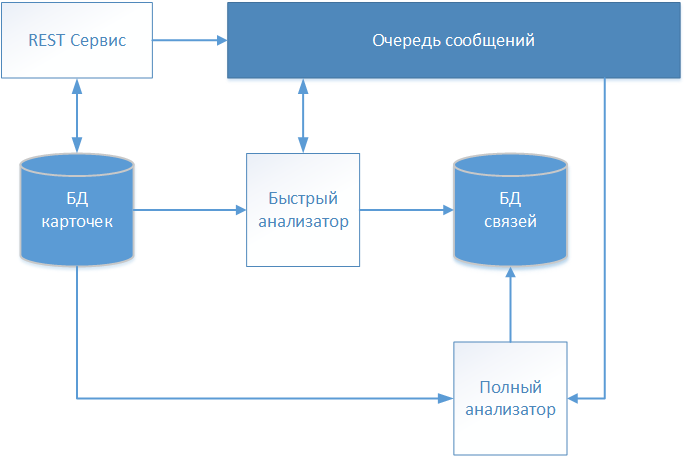
Textbeschreibungen von Patienten werden über den REST-Service akzeptiert und unverändert im Repository (Kartendatenbank) gespeichert. Da unser System mit medizinischen Daten arbeitet, wurde der FHIR- Standard (Fast Healthcare Interoperability Resources) für den Informationsaustausch gewählt. Informationen über die empfangene Patientenkarte werden zur weiteren Analyse und Entscheidungsfindung beim Aufbau der Kommunikation in die Nachrichtenwarteschlange übertragen.
Die erste Karte, die verarbeitet wird, ist der „Quick Analyzer“ , der mit einem deterministischen Algorithmus arbeitet. Wenn alle Regeln des deterministischen Algorithmus ausgearbeitet wurden, wird ein Datensatz mit einer Verknüpfung zur verarbeiteten Karte in einem separaten Speicher (Verknüpfungsdatenbank) erstellt. Der Datensatz enthält zusätzlich zur Kennung der analysierten Karte das Datum der Kommunikationsherstellung und eine bedingte Kennung, die den global identifizierten Patienten identifiziert. Weitere Karten werden weiter auf die angegebene globale Kennung bezogen, wodurch ein Array gebildet wird, das eine bestimmte Person beschreibt.
Wenn der deterministische Algorithmus keine Übereinstimmung findet, werden die Karteninformationen über die Nachrichtenwarteschlange an den „Full Analyzer“ übertragen.
( ). . :

1. -
, . 2.
2.
- , ().
3.
, , ( ) , .
4.
, . . , , . , , , .