
Mit den Eigenschaften von Primzahlen können Sie selten anders als in Form eines vorberechneten Arrays damit arbeiten - und vorzugsweise so umfangreich wie möglich. Das natürliche Speicherformat in Form von ganzen Zahlen mit der einen oder anderen Ziffernkapazität leidet gleichzeitig an einigen Nachteilen, die mit dem Wachstum des Datenvolumens signifikant werden.
Das Format von 16-Bit-Ganzzahlen ohne Vorzeichen mit der Größe einer solchen Tabelle beträgt also ungefähr 13 Kilobyte. Es enthält nur 6542 Primzahlen: gefolgt von der Zahl 65531 sind die Werte für eine höhere Bittiefe. Ein solcher Tisch ist nur als Spielzeug geeignet.
Das beliebteste 32-Bit-Integer-Format in der Programmierung sieht viel solider aus - es ermöglicht Ihnen, etwa 203 Millionen einfache zu speichern. Eine solche Tabelle belegt jedoch bereits etwa 775 Megabyte.
Das 64-Bit-Format bietet noch mehr Perspektiven. Mit einer theoretischen Potenz in der Größenordnung von 1e + 19 Werten hätte die Tabelle jedoch eine Größe von 64 Exabyte.
Es wird nicht wirklich angenommen, dass unsere fortschrittliche Menschheit in absehbarer Zeit jemals eine Tabelle mit Primzahlen eines solchen Volumens berechnen wird. Und hier geht es weniger um Volumen als um die Zählzeit der verfügbaren Algorithmen. Wenn beispielsweise die Tabelle aller einfachen 32-Bit-Tabellen in wenigen Stunden noch unabhängig berechnet werden kann (Abb. 1), dauert es mehrere Tage, bis die Tabelle um mindestens eine Größenordnung größer ist. Aber solche Bände heute - das ist nur das Anfangsniveau.
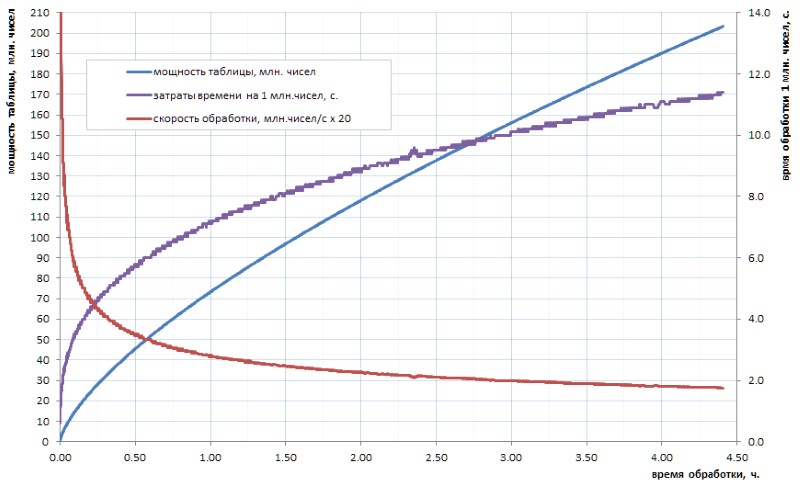
Wie aus dem Diagramm ersichtlich ist, geht die spezifische Berechnungszeit nach dem Startruck reibungslos in asymptotisches Wachstum über. Er ist ziemlich langsam. Dies ist jedoch Wachstum, was bedeutet, dass das Mining aller nächsten Daten im Laufe der Zeit immer schwieriger wird. Wenn Sie einen bedeutenden Durchbruch erzielen möchten, müssen Sie die Arbeit über die Kerne hinweg parallelisieren (und sie lässt sich gut parallelisieren) und an Supercomputer hängen. Mit der Aussicht, die ersten 10 Milliarden einfach in einer Woche und 100 Milliarden - nur in einem Jahr - zu bekommen. Natürlich gibt es schnellere Algorithmen zur einfachen Berechnung als die in meinen Hausaufgaben verwendete triviale Büste, aber im Wesentlichen ändert dies nichts an der Sache: Nach zwei oder drei Größenordnungen wird die Situation ähnlich.
Daher wäre es schön, die Zählarbeiten einmal durchgeführt zu haben, das Ergebnis in einer vorgefertigten tabellarischen Form zu speichern und bei Bedarf zu verwenden.
Aufgrund der Offensichtlichkeit der Idee stößt das Netzwerk auf viele Links zu vorgefertigten Listen von Primzahlen, die bereits von jemandem berechnet wurden. Leider sind sie in den meisten Fällen nur für Studentenhandwerk geeignet: eines davon wandert beispielsweise von Ort zu Ort und umfasst 50 Millionen einfache. Dieser Betrag kann nur Uneingeweihte in Erstaunen versetzen: Es wurde bereits oben erwähnt, dass Sie auf einem Heimcomputer in wenigen Stunden die Tabelle aller einfachen 32-Bit-Tabellen unabhängig berechnen können und sie viermal größer ist. Wahrscheinlich vor 15 bis 20 Jahren war eine solche Liste in der Tat eine heldenhafte Leistung für die Laiengemeinschaft. Im Zeitalter von Multi-Core-Multi-Gigahertz- und Multi-Gigabyte-Geräten ist dies heute nicht mehr beeindruckend.
Ich hatte das Glück, den Zugang zu einer viel repräsentativeren Tabelle einfacher zu kennen, die ich weiter als Illustration und Opfer für meine Feldversuche verwenden werde. Zum Zwecke der Verschwörung werde ich sie 1TPrimo nennen . Es enthält alle Primzahlen weniger als eine Billion.
Am Beispiel von 1TPrimo ist leicht zu erkennen, mit welchen Volumes Sie umgehen müssen. Mit einer Kapazität von rund 37,6 Milliarden Werten im 64-Bit-Integer-Format umfasst diese Liste 280 Gigabyte. Übrigens - der Teil davon, der in 32 Ziffern passen könnte, macht nur 0,5% der Anzahl der darin dargestellten Zahlen aus. Dies macht absolut klar, dass jede ernsthafte Arbeit mit Primzahlen zwangsläufig zu einer Gesamtbittiefe von 64 Bit (oder mehr) führt.
Somit ist die düstere Tendenz offensichtlich: Eine irgendwie ernste Tabelle von Primzahlen hat unvermeidlich ein Titanvolumen. Und wir müssen das irgendwie bekämpfen.
Das erste, was mir beim Betrachten einer Tabelle einfällt (Abb. 2), ist, dass sie aus nahezu identischen aufeinander folgenden Werten besteht, die sich nur in einer oder zwei der letzten Dezimalstellen unterscheiden:
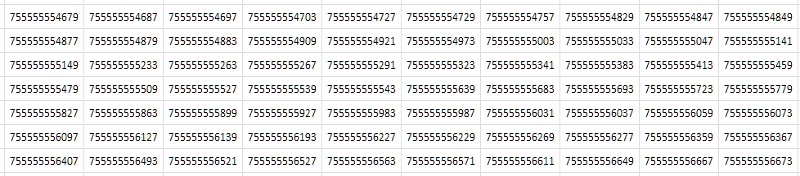
Einfach gesagt, aus den allgemeinsten, abstrakten Überlegungen: Wenn die Datei viele doppelte Daten enthält, sollte sie vom Archivierer gut komprimiert werden. In der Tat ergab die Komprimierung der 1TPrimo-Tabelle mit dem beliebten 7-Zip-Dienstprogramm bei Standardeinstellungen ein ziemlich hohes Komprimierungsverhältnis: 8,5. Die Verarbeitungszeit auf einem 8-Core-Server mit einer durchschnittlichen Auslastung aller Kerne von etwa 80 bis 90% betrug - bei der enormen Größe der Quelltabelle - 14 Stunden und 12 Minuten. Universelle Komprimierungsalgorithmen wurden für einige abstrakte, verallgemeinerte Vorstellungen von Daten entwickelt. In einigen speziellen Fällen können spezielle Komprimierungsalgorithmen, die auf den bekannten Merkmalen des eingehenden Datensatzes basieren, viel effektivere Indikatoren aufzeigen, denen diese Arbeit gewidmet ist. Und wie effektiv es wird, wird unten deutlich.
Die engen Zahlenwerte benachbarter Primzahlen erfordern eine Entscheidung, diese Werte nicht selbst zu speichern, sondern die Intervalle (Unterschiede) zwischen ihnen. In diesem Fall können erhebliche Einsparungen erzielt werden, da die Bittiefe der Intervalle viel geringer ist als die Bittiefe der Anfangsdaten (Abb. 3).
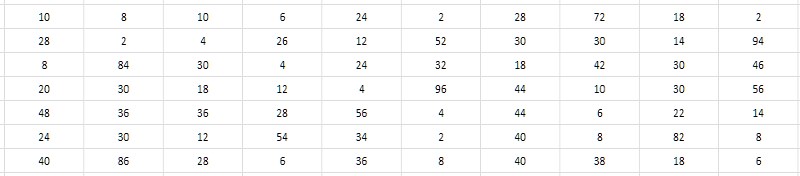
Und es scheint, dass es nicht von der Bittiefe der einfachen abhängt, die das Intervall erzeugen. Eine erschöpfende Suche zeigt, dass typische Werte von Intervallen für Primzahlen, die von verschiedenen Stellen in der 1TPrimo-Tabelle stammen, innerhalb von Einheiten, Zehnern, manchmal Hunderten liegen und - als erster Arbeitssatz - wahrscheinlich in den Bereich von 8 Bit passen könnten Ganzzahlen ohne Vorzeichen, d. h. Bytes. Dies wäre sehr praktisch und würde im Vergleich zum 64-Bit-Format sofort zu einer 8-fachen Datenkomprimierung führen - nur irgendwo auf dem Niveau, das der 7-Zip-Archivierer demonstriert. Darüber hinaus sollte die Einfachheit der Komprimierungs- und Dekomprimierungsalgorithmen im Vergleich zu 7-zip im Prinzip einen großen Einfluss auf die Geschwindigkeit der Komprimierung und den Zugriff auf Daten haben. Klingt verlockend.
Es ist absolut klar, dass die von ihren Absolutwerten in die relativen Intervalle zwischen ihnen konvertierten Daten nur zum Wiederherstellen einer Reihe von Werten geeignet sind, die vom Anfang der Primärtabelle an in einer Reihe stehen. Wenn wir einer solchen Intervalltabelle jedoch eine minimale Blockindexstruktur hinzufügen, können wir mit unbedeutenden zusätzlichen Gemeinkosten sowohl das Tabellenelement anhand seiner Nummer als auch das nächstgelegene Element anhand eines willkürlich festgelegten Werts und diese Operationen zusammen mit der Hauptoperation wiederherstellen, jedoch bereits blockweise Sequenzbeispiele - im Allgemeinen erschöpft es den Löwenanteil möglicher Abfragen zu solchen Daten. Die statistische Verarbeitung wird natürlich komplizierter, bleibt aber dennoch recht transparent Es gibt keinen besonderen Trick, es "on the fly" aus den verfügbaren Intervallen wiederherzustellen, wenn auf den erforderlichen Datenblock zugegriffen wird.
Aber leider. Ein einfaches numerisches Experiment mit 1TPrimo-Daten zeigt, dass bereits am Ende der dritten zehn Millionen (dies ist weniger als ein Hundertstel Prozent des 1TPrimo-Volumens) - und dann überall sonst - die Intervalle zwischen benachbarten Primzahlen regelmäßig außerhalb des Bereichs von 0..255 liegen.
Ein etwas kompliziertes numerisches Experiment zeigt jedoch, dass das Wachstum des maximalen Intervalls zwischen benachbarten Primzahlen mit dem Wachstum der Tabelle selbst sehr, sehr langsam ist - was bedeutet, dass die Idee in gewisser Weise immer noch gut ist.
Der zweite, genauere Blick auf die Tabelle der Intervalle legt nahe, dass es möglich ist, nicht den Unterschied selbst, sondern seine Hälfte zu speichern. Da alle Primzahlen größer als 2 offensichtlich ungerade sind, sind ihre Unterschiede offensichtlich gerade. Dementsprechend können die Differenzen ohne Wertverlust um 2 reduziert werden; und der Vollständigkeit halber kann man auch eins vom erhaltenen Quotienten subtrahieren, um den Nullwert, der nicht anders beansprucht wurde, sinnvoll zu verwenden (Fig. 4). Eine solche Verringerung der Intervalle wird im Folgenden als monolithisch bezeichnet, im Gegensatz zu der losen, porösen Ausgangsform, bei der sich herausstellte, dass alle ungeraden Werte und Null nicht beansprucht wurden.
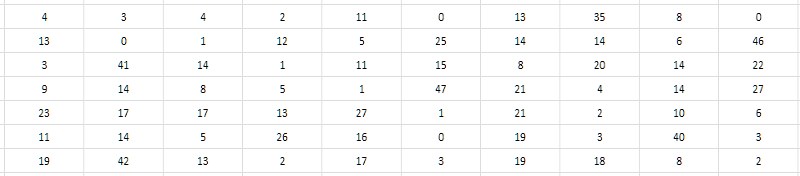
Es ist zu beachten, dass, da das Intervall zwischen den ersten beiden einfachen (2 und 3) nicht in dieses Schema passt, 2 aus der Intervalltabelle ausgeschlossen werden muss und diese Tatsache die ganze Zeit berücksichtigt wird.
Mit dieser einfachen Technik können Sie Intervalle von 2 bis 512 im Wertebereich 0..255 codieren. Wieder einmal wird die Hoffnung lebendig, dass die Differenzmethode es uns ermöglicht, eine viel leistungsfähigere Folge von Primzahlen zu packen. Und das zu Recht: Ein Lauf von 37,6 Milliarden Werten in der 1TPrimo-Liste ergab nur 6 (sechs!) Intervalle, die nicht im Bereich von 2..512 liegen.
Aber das waren gute Nachrichten; Das Schlimme ist, dass diese sechs Intervalle ziemlich frei über die Liste verteilt sind und das erste bereits am Ende des ersten Drittels der Liste auftritt, wodurch die verbleibenden zwei Drittel zu Ballast werden, der für diese Komprimierungsmethode ungeeignet ist (Abb. 5):
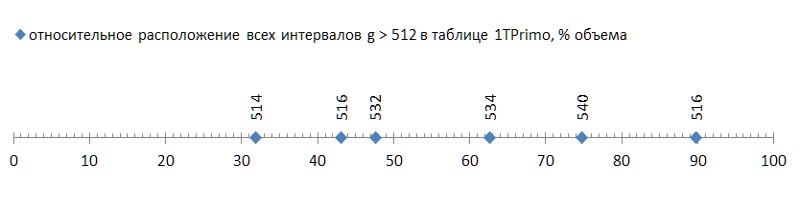
Solch ein Flush (einige unglückliche sechs Stücke für fast vierzig Milliarden! - und auf Sie ...) sogar mit einer Fliege in der Salbe zum Vergleich - um die Ehre des Teers zu zeigen. Aber leider ist dies ein Muster, kein Unfall. Wenn wir das erste Auftreten von Intervallen zwischen Primzahlen in Abhängigkeit von der Datenlänge verfolgen, wird klar, dass dieses Phänomen in der Genetik von Primzahlen liegt, obwohl es extrem langsam fortschreitet (Abb. 6 *).
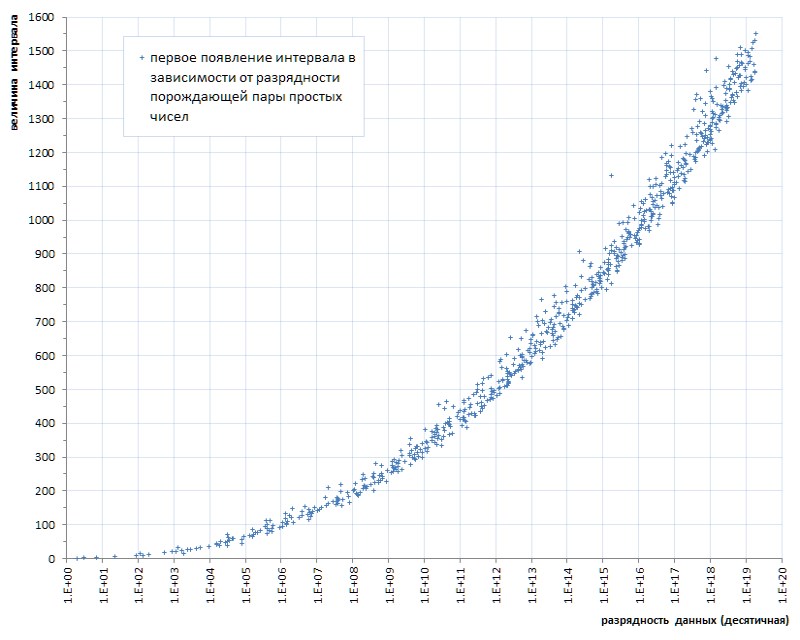
* Zeitplan zusammengestellt nach dem thematischen Ort von Thomas R. Nisley ,
Dies sind mehrere Größenordnungen besser als die Leistung der 1TPrimo-Liste
Aber auch dieser sehr langsame Fortschritt deutet eindeutig an: Man kann sich auf eine bestimmte vorgegebene Bittiefe eines Intervalls nur bei einer bestimmten vorgegebenen Potenz der Liste beschränken. Das heißt, es ist nicht als universelle Lösung geeignet.
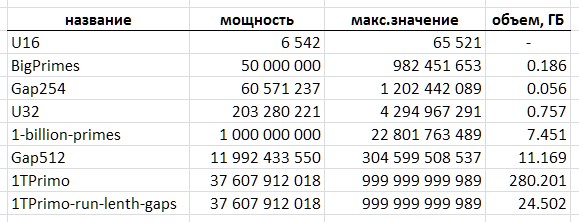
Die Tatsache, dass Sie mit der vorgeschlagenen Methode zum Komprimieren einer Folge von Primzahlen eine einfache kompakte Tabelle mit einer Kapazität von fast 12 Milliarden Werten implementieren können, ist jedoch bereits ein gutes Ergebnis. Eine solche Tabelle belegt ein Volumen von 11,1 Gigabyte - gegenüber 89,4 Gigabyte in einem trivialen 64-Bit-Format. Sicherlich kann für eine Reihe von Anwendungen eine solche Lösung ausreichend sein.
Und was interessant ist: Das Verfahren zum Übersetzen einer 64-Bit-1TPrimo-Tabelle in das Format von 8-Bit-Intervallen mit einer Blockstruktur unter Verwendung nur eines Prozessorkerns (für die Parallelisierung müssten Sie auf eine erhebliche Komplikation des Programms zurückgreifen, und es hat sich absolut nicht gelohnt) und nicht mehr als 5 % der Prozessorlast (die meiste Zeit für Dateivorgänge) dauerte nur 19 Minuten. Gegen - ich erinnere mich - 14 Stunden auf acht Kernen bei 80-90% der vom 7-Zip-Archivierer aufgewendeten Last.
Natürlich wurde nur das erste Drittel der Tabelle dieser Übersetzung unterzogen, bei der der Intervallbereich 512 nicht überschreitet. Wenn wir also die vollen 14 Stunden auf dasselbe Drittel bringen, sollten 19 Minuten mit fast 5 Stunden des 7-Zip-Archivierers verglichen werden. Bei einer vergleichbaren Komprimierung (8 und 8,5) beträgt der Unterschied etwa das 15-fache. Wenn man bedenkt, dass der Löwenanteil der Arbeitszeit des Rundfunkprogramms durch Dateivorgänge belegt war, wäre der Unterschied auf einem schnelleren Festplattensystem noch größer. Und intellektuell sollte die Betriebszeit von 7-zip auf acht Kernen immer noch auf einem Thread gezählt werden, und dann wird der Vergleich wirklich angemessen.
Die Auswahl aus einer solchen Datenbank unterscheidet sich zeitlich kaum von der Auswahl aus der Tabelle der entpackten Daten und wird fast ausschließlich durch den Zeitpunkt der Dateivorgänge bestimmt. Die spezifischen Zahlen hängen stark von der spezifischen Hardware ab. Auf meinem Server dauerte der Zugriff auf einen beliebigen Datenblock durchschnittlich 37,8 μs, während das sequentielle Lesen von Blöcken - 4,2 μs pro Block, zum vollständigen Entpacken des Blocks - weniger als 1 μs betrug. Das heißt, es macht keinen Sinn, die Dekomprimierung von Daten mit der Arbeit eines Standardarchivierers zu vergleichen. Und das ist ein großes Plus.
Und schließlich bieten die Beobachtungen eine weitere dritte Lösung, mit der alle Einschränkungen der Datenleistung beseitigt werden: Codierungsintervalle mit Werten variabler Länge. Diese Technik ist seit langem in kompressionsbezogenen Anwendungen weit verbreitet. Seine Bedeutung ist, dass, wenn in der Eingabe festgestellt wird, dass einige Werte häufig gefunden werden, einige weniger häufig sind und einige sehr selten sind, wir den ersten mit Funktionscodes, den zweiten mit authentischeren Codes und den dritten codieren können - sehr lang (vielleicht sogar sehr lang, weil es keine Rolle spielt: Trotzdem sind solche Daten sehr selten). Infolgedessen kann die Gesamtlänge der empfangenen Codes viel kürzer als die Eingabedaten sein.
Wenn wir uns bereits die grafische Darstellung des Erscheinungsbilds der Intervalle in Abb. 7 ansehen, können wir davon ausgehen, dass die Intervalle 2, 4, 6 usw. sind. erscheinen früher als Intervalle, z. B. 100, 102, 104 usw., dann sollte das erstere weiterhin viel häufiger auftreten als das letztere. Und umgekehrt - wenn die Intervalle 514 erst bei 11,99 Milliardstel, 516 - ab 16,2 Milliardstel und 518 - im Allgemeinen erst bei 87,7 Milliardstel auftreten, werden sie sehr selten auftreten. Das heißt, a priori können wir die umgekehrte Beziehung zwischen der Größe des Intervalls und seiner Häufigkeit in einer Folge von Primzahlen annehmen. Und das bedeutet - Sie können eine einfache Struktur erstellen, die Codes variabler Länge für sie implementiert.
Natürlich sollten Statistiken über die Häufigkeit von Intervallen für die Wahl einer bestimmten Codierungsmethode entscheidend sein. Glücklicherweise ist im Gegensatz zu willkürlichen Daten die Häufigkeit von Intervallen zwischen Primzahlen - die an sich ein für alle Mal streng bestimmt sind - auch ein genau bestimmtes, ein für alle Mal definiertes Merkmal.
Abbildung 7 zeigt den Frequenzgang der Intervalle für die gesamte 1TPrimo-Liste:
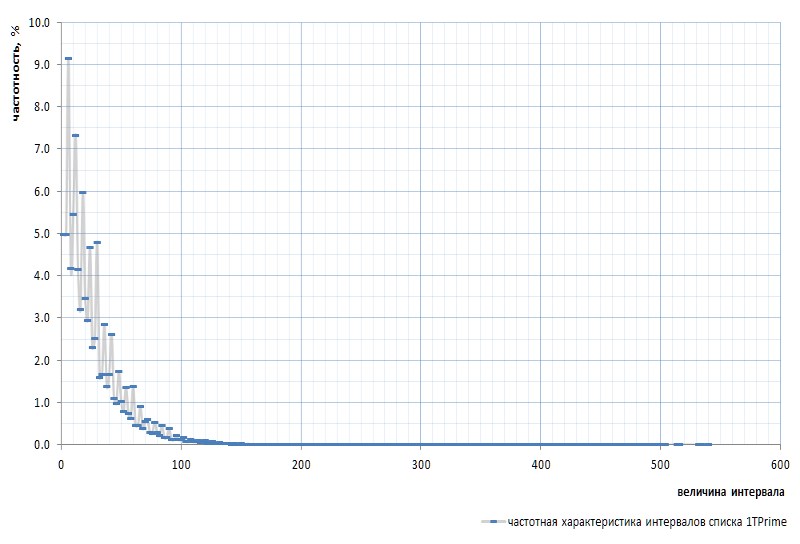
Hier muss noch einmal erwähnt werden, dass das Intervall zwischen den allerersten Primzahlen 2 und 3 aus dem Diagramm ausgeschlossen ist: Dieses Intervall ist 1 und tritt unabhängig von der Potenz der Liste genau einmal in der Folge von Primzahlen auf. Dieses Intervall ist so eigenartig, dass es einfacher ist, 2 aus der Liste der einfachen zu entfernen, als ständig zu Reservierungen abzuweichen. Die Sim wird als virtuelle Primzahl deklariert: Sie ist in den Listen nicht sichtbar, aber vorhanden. Wie dieser Gopher.
Auf den ersten Blick bestätigt der Frequenzgraph die in einigen Absätzen oben genannte a priori-Annahme vollständig. Es zeigt deutlich die statistische Heterogenität der Intervalle und die hohe Häufigkeit kleiner Werte im Vergleich zu großen. In der zweiten, konvexeren Ansicht erweist sich die Grafik jedoch als viel interessanter (Abb. 8):
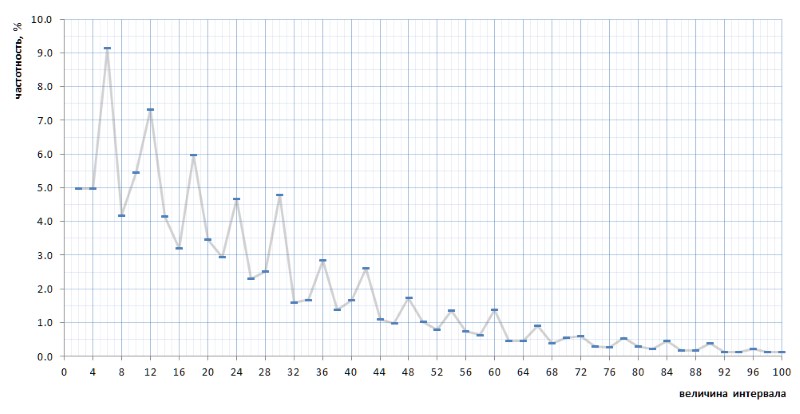
Ganz unerwartet stellt sich heraus, dass die häufigsten Intervalle nicht 2 und 4 sind, wie es aus allgemeinen Überlegungen zu sein schien, sondern 6, 12 und 18, gefolgt von 10 - und erst dann 2 und 4 mit nahezu gleicher Häufigkeit (Unterschied in 7 Ziffern) nach dem Dezimalpunkt). Darüber hinaus wird die Vielzahl der Spitzenwerte der Zahl 6 im gesamten Diagramm verfolgt.
Noch interessanter ist, dass diese versehentlich aufgedeckte Natur des Graphen universell ist - und in allen Details mit all ihren Knicken - über die gesamte Folge einfacher Intervalle, die durch die 1TPrimo-Liste dargestellt werden, wahrscheinlich für jede Folge einfacher Intervalle universell ist (natürlich Eine solch kühne Aussage bedarf eines Beweises, den ich mit großer Freude auf die Schultern von Spezialisten für Zahlentheorie übertrage. Abbildung 10 zeigt einen Vergleich der vollständigen Intervallstatistik (scharlachrote Linie) mit Stichproben mit begrenztem Intervall, die an mehreren beliebigen Stellen in der 1TPrimo-Liste (Linien anderer Farben) entnommen wurden:
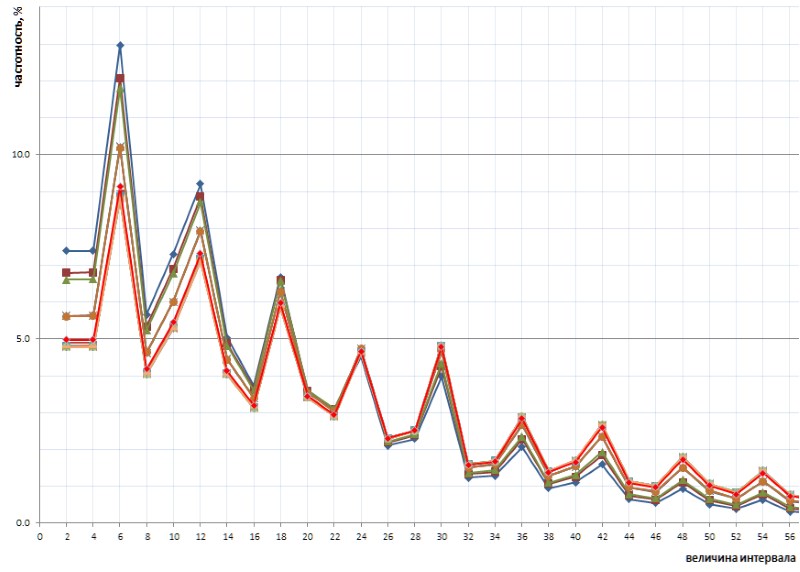
Aus dieser Grafik ist ersichtlich, dass sich alle diese Proben genau wiederholen, mit nur einem geringen Unterschied im linken und rechten Teil der Figur: Sie scheinen leicht gegen den Uhrzeigersinn um den Intervallpunkt mit einem Wert von 24 gedreht zu sein. Diese Drehung ist wahrscheinlich auf die Tatsache zurückzuführen, dass die höhere links Teile der Grafik basieren auf Samples mit geringerer Bittiefe. In solchen Samples gibt es noch gar keine oder große Intervalle sind selten, die in Samples mit höheren Bittiefen häufig auftreten. Dementsprechend spricht ihre Abwesenheit für die Häufigkeit von Intervallen mit niedrigeren Werten. In Samples mit höheren Bittiefen erscheinen viele neue Intervalle mit großen Werten, daher nimmt die Häufigkeit kleinerer Intervalle geringfügig ab. Höchstwahrscheinlich verschiebt sich der Drehpunkt mit zunehmender Leistung der Liste in Richtung größerer Werte. Irgendwo daneben befindet sich der Gleichgewichtspunkt des Graphen, an dem die Summe aller Werte auf der rechten Seite ungefähr gleich der Summe aller Werte auf der linken Seite ist.
Diese interessante Natur der Häufigkeit von Intervallen legt nahe, die triviale Struktur von Codes variabler Länge aufzugeben. Typischerweise besteht eine solche Struktur aus einem Paket von Bits verschiedener Längen und Zwecke. Zum Beispiel kommt zuerst eine bestimmte Anzahl von Präfixbits, die auf einen bestimmten Wert gesetzt sind, zum Beispiel 0. Dahinter befindet sich ein Stoppbit, das die Vervollständigung des Präfixes anzeigen und dementsprechend vom Präfix abweichen sollte: 1 in diesem Fall. Das Präfix darf keine Länge haben, dh immer wieder kann die Abtastung sofort mit einem Stoppbit beginnen, wodurch die kürzeste Sequenz bestimmt wird. Auf das Stoppbit folgt normalerweise ein Suffix, dessen Länge in gewisser Weise durch die Länge des Präfixes bestimmt wird. , , — . , - . - (, , - ) , .
, .
Und hier sollte noch etwas Wichtiges gesagt werden. Auf den ersten Blick impliziert die beobachtete Zyklizität die Aufteilung der Intervalle in Tripel: {2,4, 6 } , {8,10, 12 } , {14,16, 18 } usw. (die Werte mit der maximalen Häufigkeit in jedem Tripel sind fett markiert). . Tatsächlich ist der Zyklus hier jedoch etwas anders.
Ich werde nicht die ganze Argumentationslinie zitieren, die in der Tat nicht vorhanden ist: Es war eine intuitive Vermutung, ergänzt durch eine Methode zur stumpfen Aufzählung von Optionen, Berechnungen und Stichproben, die zeitweise mehrere Tage dauerte. Die als Ergebnis offenbarte Zyklizität besteht aus sechs Intervallen {2,4, 6 ,8,10, 12 } , {14,16, 18 ,20,22, 24 } , {26,28, 30 ,32,34, 36 } und usw. (Intervalle mit maximaler Frequenz sind wieder fett hervorgehoben).
Kurz gesagt, der vorgeschlagene Verpackungsalgorithmus lautet wie folgt.
Durch Teilen der Intervalle in Sechser mit geraden Zahlen können wir jedes Intervall g in der Form g = i * 12 + t , wobei i der Index der Sechs ist, zu denen dieses Intervall gehört ( i = {0,1,2,3, ...} ) und t ist ein Schwanz, der einen der Werte aus einem fest definierten, begrenzten und identischen Wert für sechs der Menge darstellt {2,4,6,8,10,12} . Der Frequenzgang des oben hervorgehobenen Index ist fast genau umgekehrt proportional zu seinem Wert. Daher ist es logisch, den Sechs-Index in eine triviale Struktur eines Codes variabler Länge umzuwandeln, für die oben ein Beispiel angegeben ist. Die Frequenzcharakteristik des Endes ermöglicht es Ihnen, ihn in zwei Gruppen zu unterteilen, die mit Bitketten unterschiedlicher Länge codiert werden können: Die am häufigsten gefundenen Werte 6 und 12 werden mit einem Bit codiert, die Werte 2, 4, 8 und 10, die viel seltener auftreten, werden mit zwei Bits codiert. Natürlich wird ein weiteres Bit benötigt, um zwischen diesen beiden Optionen zu unterscheiden.
Ein Array, das Bitpakete enthält, wird durch feste Felder ergänzt, die die Startwerte der im Block dargestellten Daten angeben, sowie durch andere Größen, die erforderlich sind, um eine beliebige einfache oder eine Folge einfacher aus den im Block gespeicherten Intervallen wiederherzustellen.
Zusätzlich zu dieser Blockindexstruktur wird die Verwendung von Codes variabler Länge durch die zusätzlichen Kosten im Vergleich zu Intervallen mit festen Bits erschwert.
Bei Verwendung von Intervallen fester Größe ist das Bestimmen des Blocks, in dem nach einer Primzahl gesucht werden soll, anhand seiner Seriennummer eine ziemlich einfache Aufgabe, da die Anzahl der Intervalle pro Block im Voraus bekannt ist. Die Suche nach einer einfachen Lösung zum nächstgelegenen Wert hat jedoch keine direkte Lösung. Alternativ können Sie eine empirische Formel verwenden, mit der Sie die ungefähre Blocknummer mit dem erforderlichen Intervall ermitteln können. Danach müssen Sie durch umfassende Suche nach dem gewünschten Block suchen.
Für eine Tabelle mit Codes variabler Länge ist für beide Aufgaben der gleiche Ansatz erforderlich: sowohl zum Abrufen eines Werts nach Zahlen als auch zum Suchen nach Werten. Da die Länge der Codes variiert, ist nie vorher bekannt, wie viele Unterschiede in einem bestimmten Block gespeichert sind und in welchem Block der gewünschte Wert liegt. Es wurde experimentell festgestellt, dass mit einer Blockgröße von 512 Bytes (einschließlich einiger Header-Bytes) die Blockkapazität bis zu 10-12 Prozent des Durchschnittswerts betragen kann. Kleinere Blöcke ergeben eine noch größere relative Streuung. Gleichzeitig neigt der Durchschnittswert der Blockkapazität selbst dazu, langsam zu sinken, wenn die Tabelle wächst. Die Auswahl empirischer Formeln zur ungenauen Bestimmung des Anfangsblocks zur Suche nach dem gewünschten Wert sowohl nach Anzahl als auch nach Wert ist keine triviale Aufgabe. Alternativ können Sie eine komplexere und komplexere Indizierung verwenden.
Das ist in der Tat alles.
Im Folgenden werden die Feinheiten der Komprimierung einer Primärtabelle unter Verwendung von Codes variabler Länge und die damit verbundenen Strukturen auf formellere und detailliertere Weise beschrieben, und der Code für die Funktionen des Packens und Entpackens von Intervallen in C wird angegeben.
Das Ergebnis.
Die Datenmenge, die aus Tabelle 1TPrimo in Codes variabler Länge übersetzt wurde, ergänzt durch eine Blockindexstruktur, die ebenfalls nachstehend beschrieben wird, betrug 26.309.295.104 Bytes (24,5 GB), dh das Komprimierungsverhältnis erreicht 11,4. Offensichtlich nimmt mit zunehmender Bittiefe das Kompressionsverhältnis zu.
Die Sendezeit von 280 GB 1TPrimo-Tabelle im neuen Format betrug 1 Stunde. Dies ist das erwartete Ergebnis nach Experimenten mit Packungsintervallen in Einzelbyte-Ganzzahlen. In beiden Fällen besteht die Übersetzung der Quelltabelle hauptsächlich aus Dateioperationen und lädt den Prozessor fast nicht (im zweiten Fall ist die Last aufgrund der höheren Rechenkomplexität des Algorithmus immer noch höher). Die Datenzugriffszeit unterscheidet sich auch nicht sehr von Einzelbyte-Intervallen, aber die Zeit zum Entpacken eines vollständigen Blocks derselben Größe dauerte aufgrund der höheren Komplexität des Algorithmus zum Extrahieren von Codes variabler Länge 1,5 μs.
Die Tabelle (Abb. 10) fasst die volumetrischen Eigenschaften der in diesem Text genannten Primzahlentabellen zusammen.
Beschreibung des Komprimierungsalgorithmus
Bedingungen und Notation
P (prime): P1=3, P2=5, P3=7 ... Pn, Pn1 sind Primzahlen gemäß ihrer Seriennummer. Noch einmal (und zum letzten Mal) betone ich, dass
P0=2 eine virtuelle Primzahl ist; Aus Gründen der formalen Einheitlichkeit wird diese Zahl physisch von der Liste der Primzahlen ausgeschlossen.
G (gap) - das Intervall zwischen zwei aufeinanderfolgenden Primzahlen Gn = Pn1 - Pn; G={2,4,6,8 ...} Gn = Pn1 - Pn; G={2,4,6,8 ...} .
D (dense) - reduziert auf ein monolithisches Formintervall: D = G/2 -1; D={0,1,2,3 ...} D = G/2 -1; D={0,1,2,3 ...} . Die sechs Intervalle in der monolithischen Form sehen aus wie {0,1,2,3,4,5}, {6,7,8,9,10,11}, {12,13,14,15,16,17} usw.
Q (quotient) - Index der sechs auf eine monolithische Form reduziert, Q = D div 6; Q={0,1,2,3 ...} Q = D div 6; Q={0,1,2,3 ...}
R (remainder) - der Rest der monolithischen sechs R = D mod 6. R immer einen Wert im Bereich {0,1,2,3,4,5} .
Die Q und R Werte, die durch das obige Verfahren aus einem beliebigen Intervall G aufgrund ihrer stabilen Frequenzeigenschaften erhalten werden, unterliegen einer Komprimierung und Speicherung in Form von Bitpaketen variabler Länge, die nachstehend beschrieben werden. Die Bitfolgen, die die Werte von Q und R in einem Paket codieren, werden auf verschiedene Arten erzeugt: Zum Codieren des Q Index wird die Bitkette des Präfixes H , des Flusses F und des Hilfsbits S , und die Bitgruppe des Infix X und des Hilfsbits A werden verwendet, um den Rest R zu codieren R
A (arbiter) - ein Bit, das die Größe des Infix X : 0 - Ein-Bit-Infix, 1 - Zwei-Bit.
X (infix) - 1- oder 2-Bit-Infix zusammen mit dem Arbiter-Bit R tabellarisch gegenseitig bestimmt (die Tabelle zeigt auch die Häufigkeit der ersten sechs mit solchen Infixen als Referenz):
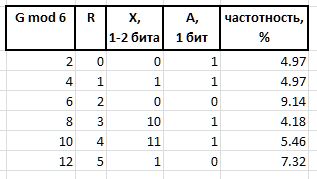
F (fluxion) ist ein Fluxion, eine Ableitung des Index Q variabler Länge L={0,1,2...} , der zur Unterscheidung zwischen der Semantik von Bitfolgen (), 0, 00, 000, oder 1, 01, 001 usw. dient. d.
Eine Bitkette von Einheiten der Länge L wird ausgedrückt als 2^L - 1 (das Vorzeichen ^ bedeutet Exponentiation). In der C-Notation kann der gleiche Wert durch den Ausdruck 1<<L - 1 . Dann kann der Wert der Fluxia der Länge L Q Ausdruck aus Q
F = Q - (1 << L - 1),
und Q aus Fluxia durch Ausdruck wiederherstellen
Q = (1 << L - 1) + F.
Beispielsweise werden für die Größen Q = {0..15} die folgenden Fluxia-Bitketten erhalten:
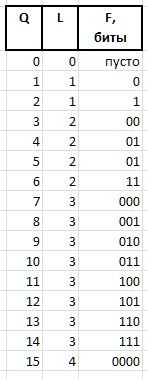
Die letzten beiden Bitfelder, die zum Packen / Wiederherstellen von Werten erforderlich sind, sind:
H (header) - Präfix, eine auf 0 gesetzte Bitfolge.
S (stop) - Stoppbit auf 1 gesetzt, wodurch das Präfix beendet wird.
Tatsächlich werden diese Bits zuerst in Bitfolgen verarbeitet. Sie ermöglichen es Ihnen, beim Entpacken oder beim Packen die Größe des Flusses und den Beginn der Arbiter- und Flussfelder zu bestimmen - unmittelbar nach dem Stoppbit.
W (width) - die Breite des gesamten Codes in Bits.
Die vollständige Struktur des Bitpakets ist in Fig. 11 gezeigt:
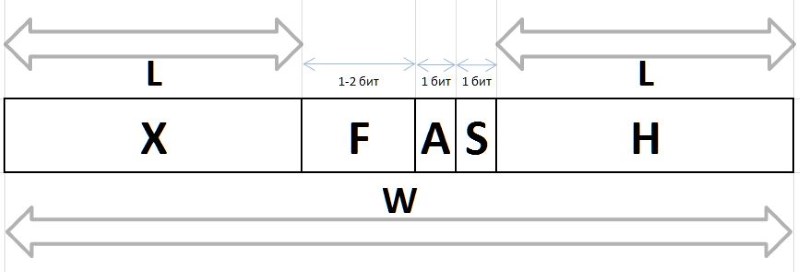
Die aus diesen Ketten wiederhergestellten Werte von Q und R ermöglichen es uns, den Anfangswert des Intervalls wiederherzustellen:
D = Q * 6 + R,
G = (D + 1) * 2,
und die Folge von wiederhergestellten Intervallen ermöglicht es Ihnen, die ursprünglichen Primzahlen von einem gegebenen Basiswert des Blocks (Startblock von Intervallen) wiederherzustellen, indem Sie alle Intervalle dieses Blocks nacheinander hinzufügen.
Um mit Bitfolgen zu arbeiten, wird eine 32-Bit-Ganzzahlvariable verwendet, in der die niedrigstwertigen Bits verarbeitet werden und nach deren Verwendung die Bits beim Packen nach links oder beim Entpacken nach rechts verschoben werden.
Blockstruktur
Zusätzlich zu Bitfolgen enthält ein Block Informationen, die zum Abrufen oder Hinzufügen von Bits sowie zum Bestimmen des Inhalts eines Blocks erforderlich sind.
// // typedef unsigned char BYTE; typedef unsigned short WORD; typedef unsigned int LONG; typedef unsigned long long HUGE; typedef int BOOL; #define TRUE 1 #define FALSE 0 #define BLOCKSIZE (256) // : , #define HEADSIZE (8+8+2+2+2) // , #define BODYSIZE (BLOCKSIZE-HEADSIZE) // . // typedef struct { HUGE base; // , HUGE card; // WORD count; // WORD delta; // base+delta = WORD offset; // BYTE body[BODYSIZE]; // } crunch_block; // , put() get() crunch_block block; // . // NB: len/val rev/rel // , , // . static struct tail_t { BYTE len; // S A BYTE val; // , A - S BYTE rev; // BYTE rel; // } tails[6] = { { 4, 3, 2, 3 }, { 4, 7, 5, 3 }, { 3, 1, 0, 4 }, { 4,11, 1, 4 }, { 4,15, 3, 4 }, { 3, 5, 4, 4 } }; // BOOL put(int gap) { // 1. int Q, R, L; // (), (), int val = gap / 2 - 1; Q = val / 6; R = val % 6; L = -1; // .., 0 - 1 val = Q + 1; while (val) { val >>= 1; L++; } // L val = Q - (1 << L) + 1; // val <<= tails[R].len; val += tails[R].val; // val <<= L; // L += L + tails[R].len; // // 2. val L buffer put_index if (block.offset + L > BODYSIZE * 8) // ! return FALSE; Q = (block.offset / 8); // , R = block.offset % 8; // block.offset += L; // block.count++; // block.delta += gap; if (R > 0) // { val <<= R; val |= block.body[Q]; L += R; } // L = L / 8 + ((L % 8) > 0 ? 1 : 0); // while (L-- > 0) { block.body[Q++] = (char)val; val >>= 8; } return TRUE; } // int get_index; // // int get() { if (get_index >= BODYSIZE * 8) return 0; // int val = *((int*)&block.body[get_index / 8]) >> get_index % 8; // 4 if (val == 0) return -1; // ! int Q, R, L, F, M, len; // , , , , L = 0; while (!(val & 1)) { val >>= 1; L++; } // - if ((val & 3) == 1) // R = (val >> 2) & 1; // else R = ((val >> 2) & 3) + 2; // len = tails[R].rel; get_index += 2 * L + len; val >>= len; M = ((1 << L) - 1); // F = val & M; // Q = F + M; // return 2 * (1 + (6 * Q + tails[R].rev)); // }
Verbesserungen
Wenn wir die erhaltene Basis von Intervallen demselben 7-Zip-Archivierer zuführen, gelingt es ihm in anderthalb Stunden intensiver Arbeit auf einem 8-Core-Server, die Eingabedatei um fast 5% zu komprimieren. Das heißt, in der Datenbank der Intervalle variabler Länge aus Sicht des Archivierers besteht immer noch eine gewisse Redundanz. Es gibt also Grund, ein wenig (im guten Sinne des Wortes) über das Thema der weiteren Reduzierung der Datenredundanz zu spekulieren.
Der fundamentale Determinismus der Folge von Intervallen zwischen Primzahlen ermöglicht es, die Codierungseffizienz mit der einen oder anderen Methode genau zu berechnen. Insbesondere kleine (und eher chaotische) Skizzen ermöglichten es, eine grundlegende Schlussfolgerung über die Vorteile der Codierung von Sechsern gegenüber Tripeln und über die Vorteile der vorgeschlagenen Methode gegenüber trivialen Codes variabler Länge zu ziehen (Abb. 12):
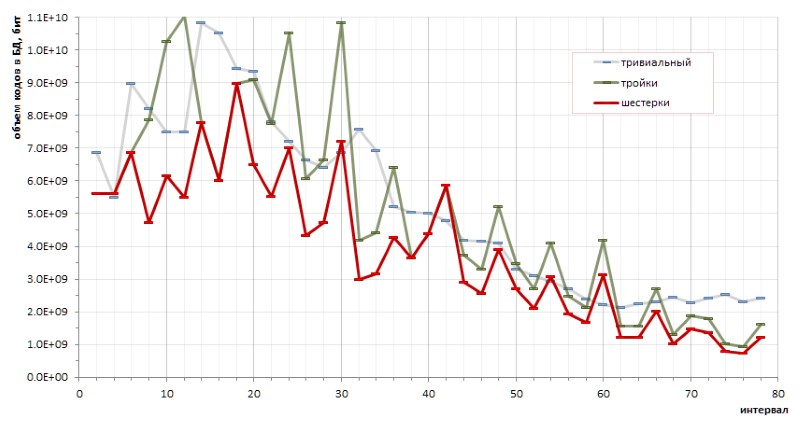
Die störenden Höhen des roten Diagramms deuten jedoch transparent darauf hin, dass es möglicherweise andere Codierungsmethoden gibt, die das Diagramm noch sanfter machen würden.
Eine andere Richtung schlägt vor, die Häufigkeit aufeinanderfolgender Intervalle zu überprüfen. Aus allgemeinen Überlegungen: Da die Intervalle 6, 12 und 18 in einer Population von Primzahlen am häufigsten vorkommen, werden sie wahrscheinlich häufiger in Paaren (Dubletts), Tripeln (Tripletts) und ähnlichen Intervallkombinationen gefunden. Wenn sich herausstellt, dass die Wiederholbarkeit von Duplets (und vielleicht sogar Triplets ... nun, plötzlich!) In der Gesamtmasse der Intervalle statistisch signifikant ist, ist es sinnvoll, sie in einen separaten Code zu übersetzen.
Das vollständige Experiment zeigt eine gewisse Vorherrschaft einzelner Dubletts gegenüber anderen. Wenn jedoch die absolute Führung für das Paar erwartet wird (6,6) - 1,37% aller Dubletten -, dann sind die anderen Gewinner dieser Bewertung viel weniger offensichtlich:
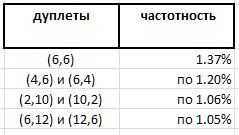
Und da das Dublett (6,6) symmetrisch ist und alle anderen notierten Dubletts asymmetrisch sind und in der Rangfolge von Spiegelzwillingen mit derselben Häufigkeit gefunden werden, sollte der Datensatz des Dubletts (6,6) in dieser Reihe in zwei Hälften zwischen nicht unterscheidbaren Zwillingen (6,6) und (6,6) , womit sie 0,68% weit bis an den Rand der Preisliste reichen. Und dies bestätigt erneut die Beobachtung, dass keine echten Vermutungen über Primzahlen ohne Überraschungen möglich sind.
Die Statistik der Drillinge zeigt auch die Führung solcher Dreifachintervalle, die nicht ganz in die spekulative Annahme passen, die von der höchsten Häufigkeit der Intervalle 6, 12, 18 ausgeht. In abnehmender Reihenfolge der Popularität sehen die Frequenzleiter unter den Drillingen wie folgt aus:

usw.
Ich befürchte jedoch, dass die Ergebnisse meiner Spekulationen für Programmierer weniger interessant sein werden als für Mathematiker, möglicherweise aufgrund der unerwarteten Korrekturen, die durch die Praxis in intuitive Vermutungen vorgenommen wurden. Es ist unwahrscheinlich, dass es möglich sein wird, eine wesentliche Dividende aus dem genannten Prozentsatz der Frequenz zugunsten einer weiteren Erhöhung des Kompressionsverhältnisses herauszuholen, während die Komplexität des Algorithmus sehr stark zu wachsen droht.
Einschränkungen
Es wurde bereits oben angemerkt, dass der Anstieg des Maximalwerts der Intervalle in Verbindung mit der Kapazität von Primzahlen sehr, sehr langsam ist. Insbesondere ist aus Fig. 6 ersichtlich, dass das Intervall zwischen beliebigen Primzahlen, die im Format einer 64-Bit-Ganzzahl ohne Vorzeichen dargestellt werden können, offensichtlich weniger als 1600 beträgt.
Mit der beschriebenen Implementierung können Sie alle 18-Bit-Intervallwerte korrekt verpacken und entpacken (tatsächlich tritt der erste Verpackungsfehler mit einem Eingabeintervall von 442358 auf). Ich habe nicht genug Vorstellungskraft, um anzunehmen, dass die Datenbank der Primintervalle auf solche Werte anwachsen kann: Nebenbei sind es etwa 100-Bit-Ganzzahlen, und um die Faulheit genauer zu berechnen. In einem Brandfall ist es nicht schwierig, den Intervallbereich zeitweise zu erweitern.
Vielen Dank für das Lesen zu diesem Ort :)