Während des Betriebs ist das Getriebe, mit dem Energie vom Motor auf die Räder übertragen wird, ziemlich laut. Der erste Grund für diesen unerwünschten Effekt besteht darin, dass die Quer- und Axialkräfte, die sich aus der Übertragung von Energie von einer Welle auf eine andere mittels eines Zahnrads ergeben, eine unerwünschte mechanische Wirkung auf die Lager und das Gehäuse haben. Der zweite Grund ist die Flexibilität verschiedener Komponenten des Getriebes, einschließlich Lager und Gehäuse, die ebenfalls zu Vibrationen führen können. Die variable Steifigkeit der Zahnradkupplung im Getriebe bewirkt eine konstante Vibration, die auf das Gehäuse übertragen wird, die wiederum vibriert und Energie auf das umgebende Fluid, beispielsweise Getriebeöl, überträgt, was dazu führt, dass Schallwellen darin angeregt werden.

Um den Geräuschpegel in solch komplexen dynamischen Systemen in den frühen Entwurfsphasen effektiv zu reduzieren, greifen Entwicklungsingenieure häufig auf numerische Simulationen zurück. Unter dem Fräser beschreiben und zeigen wir am Beispiel eines synchronisierten mechanischen 5-Gang-Getriebes die Methodik einer solchen Studie in COMSOL Multiphysics ^® , die eine Festigkeitsanalyse des mechanischen Kontakts des Getriebes, eine Analyse der Dynamik der Mehrkörpergetriebebaugruppe und eine akustische Analyse des vom Arbeitsgetriebe im umgebenden Raum erzeugten Geräusches umfasst.

Visualisierung des von einem Arbeitsgetriebe erzeugten Klangs

Schritt 1. Berechnung des mechanischen Kontakts im Getriebe

Das Getriebe, das wir als elastisch betrachten, ist eine Quelle ständiger Vibration. Aus diesem Grund ist es notwendig, die Steifigkeit der Zahnräder in verschiedenen Positionen zu bewerten. Die Zähne werden während des Betriebs verformt, und eine Reihe von stationären Festigkeitsberechnungen wird für verschiedene Drehwinkel durchgeführt, um zu bestimmen, wie sich die Steifheit während des Kupplungszyklus ändert. Zur Berechnung wird die Strafmethode auf den Kontakt angewendet, und die Einschränkungen werden für die Berücksichtigung von Drehzahnrädern festgelegt, aufgrund derer Kontaktkräfte entstehen.

Die charakteristischen Ergebnisse am Ausgang einer solchen Analyse in Form der Mises-Spannungsverteilung im Zahnradpaar zeigen hohe Spannungswerte an den Kontaktpunkten und in den Zahnbasen (Abb. 1, links). Darüber hinaus ermöglicht die Berechnung die Beobachtung und Analyse der Änderung der Steifigkeit des Getriebes während der Wellendrehung (Abb. 1, rechts).

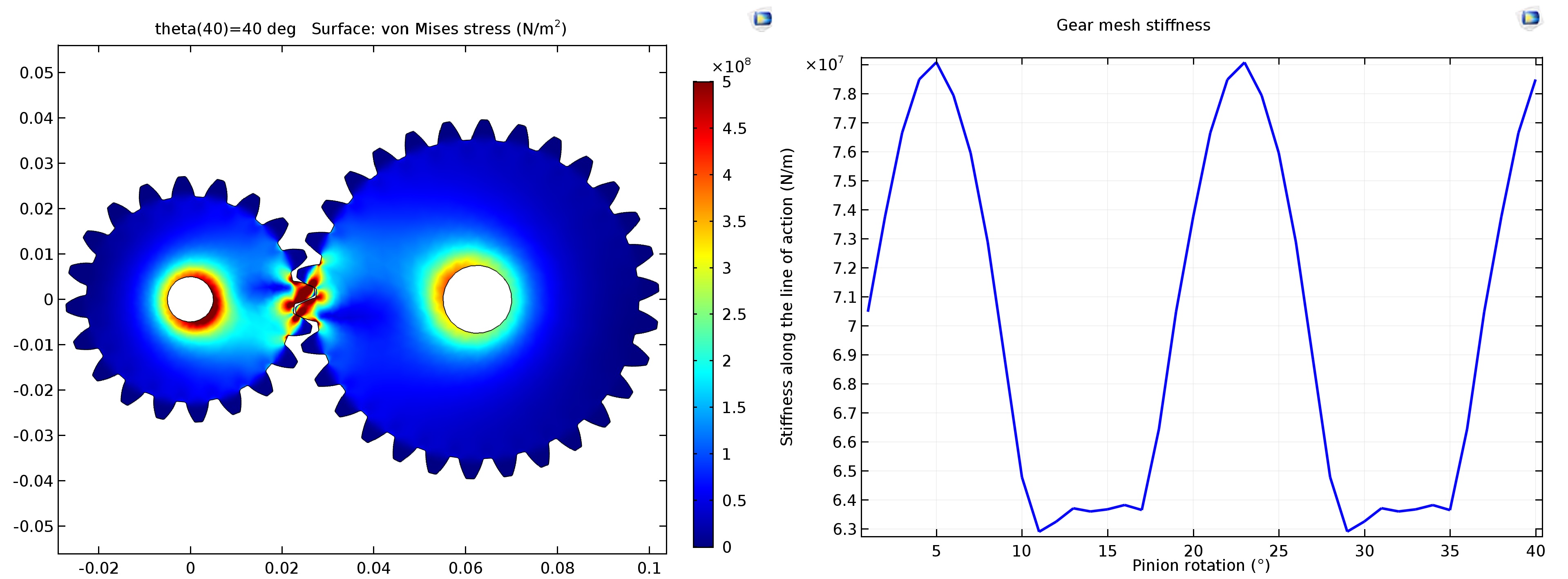
Abb. 1. Links: Mises Spannungsverteilung in einem Zahnradpaar. Rechts: Änderung der Steifigkeit der Zahnradkupplung während der Wellendrehung.

Schritt 2. Analyse eines Mehrkörpersystems aus Wellen, Zahnrädern und Gehäuse

Die Analyse von Mehrkörpersystemen wird im Zeitbereich für eine vollständige Umdrehung der Antriebswelle durchgeführt, wobei die Steifigkeit der Zahnradkupplung berücksichtigt wird, die bei der Berechnung des Kontakts im ersten Schritt vorhergesagt wurde. Diese Analyse ist erforderlich, um die Dynamik der Zahnräder und die Werte der resultierenden Schwingungen zu berechnen, die auf das Gehäuse übertragen werden. In diesem Beispiel wird die Analyse bei einer Motordrehzahl von 5000 U / min und einem Ausgangsdrehmoment von 2000 Nm durchgeführt. Die Berechnung wird unter der Annahme durchgeführt, dass die Wellen und Zahnräder mit Ausnahme der Zahnradkupplung, deren Steifigkeit einer früheren Untersuchung des mechanischen Kontakts entnommen wurde, vollkommen steif sind. Ein Körper aus Baustahl wird als elastischer Körper angesehen.

Die Mises-Spannungsverteilung im Gehäuse unter Einwirkung der von den Antriebs- und Zwischenwellen übertragenen Kräfte sowie die normale Beschleunigung des Vibrationsgehäuses, die die Ursache für Geräuschstrahlung ist, sind in Abb. 1 dargestellt. 2.

Abb. 2. Links: Mises Spannungsverteilung im Gehäuse. Rechts: normale Beschleunigung auf der Körperoberfläche.

In Abb. 3 zeigt ein Zeitdiagramm der normalen Beschleunigung an einem der Punkte im oberen Teil des Körpers und seines Frequenzspektrums. Die Frequenzen, bei denen das Gehäuse mit der größten Amplitude schwingt, liegen im Bereich zwischen 1500 und 2000 Hz.

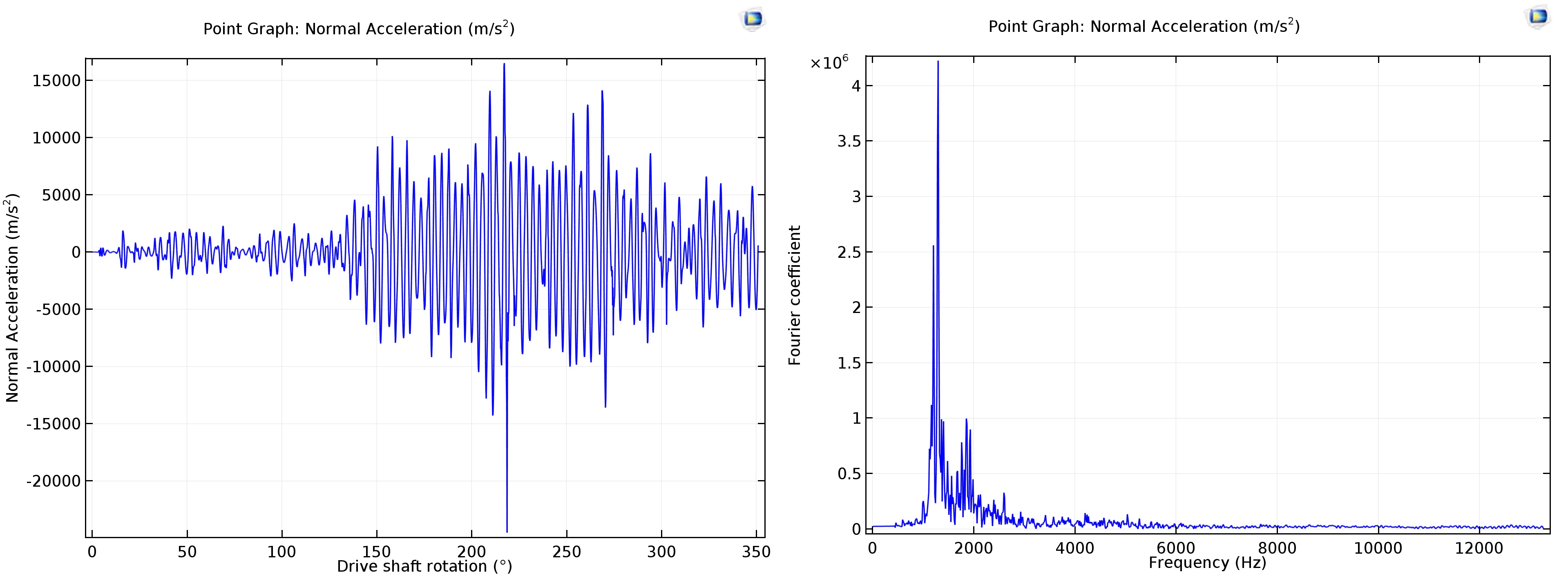
Abb. 3. Normale Beschleunigung an einem Punkt auf der Körperoberfläche. Links: Zeitdiagramm. Rechts: Sein Frequenzspektrum.

Schritt 3. Akustische Berechnung der Geräuschstrahlung vom Gehäuse

Die normale Rumpfbeschleunigung, die durch Analyse der Dynamik von Mehrkörpersystemen erhalten wird, kann dann in der akustischen Forschung als Geräuschquelle verwendet werden. Mithilfe von Untersuchungen im Frequenzbereich können Sie den Schalldruckpegel außerhalb des Getriebes vorhersagen. Da die normalen Beschleunigungswerte im Zeitbereich erhalten werden, werden sie mit der direkten schnellen Fourier-Transformation (FFT) in den Frequenzbereich umgewandelt. Um den Schalldruck zu berechnen, sollte das Getriebe von einem Luftbereich umgeben sein. Um die Größe des Berechnungsbereichs zu verringern, ohne die Genauigkeit der Ergebnisse zu verringern, wird eine Sommerfeld-Strahlungsbedingung für sphärische Wellenfronten an die Außengrenzen des Luftbereichs angelegt, damit ausgehende Schallwellen den Simulationsbereich mit minimaler Reflexion verlassen können.

Mit der Berechnung können Sie Daten zum Schalldruckpegel auf der Gehäuseoberfläche und in der Nahzone erhalten (Abb. 4). Aus den Darstellungen der Fernzone in verschiedenen Ebenen und in einer Entfernung von 1 m können Sie die vorherrschende Richtung der Geräuschstrahlung bei einer ausgewählten Frequenz ermitteln (Abb. 5).

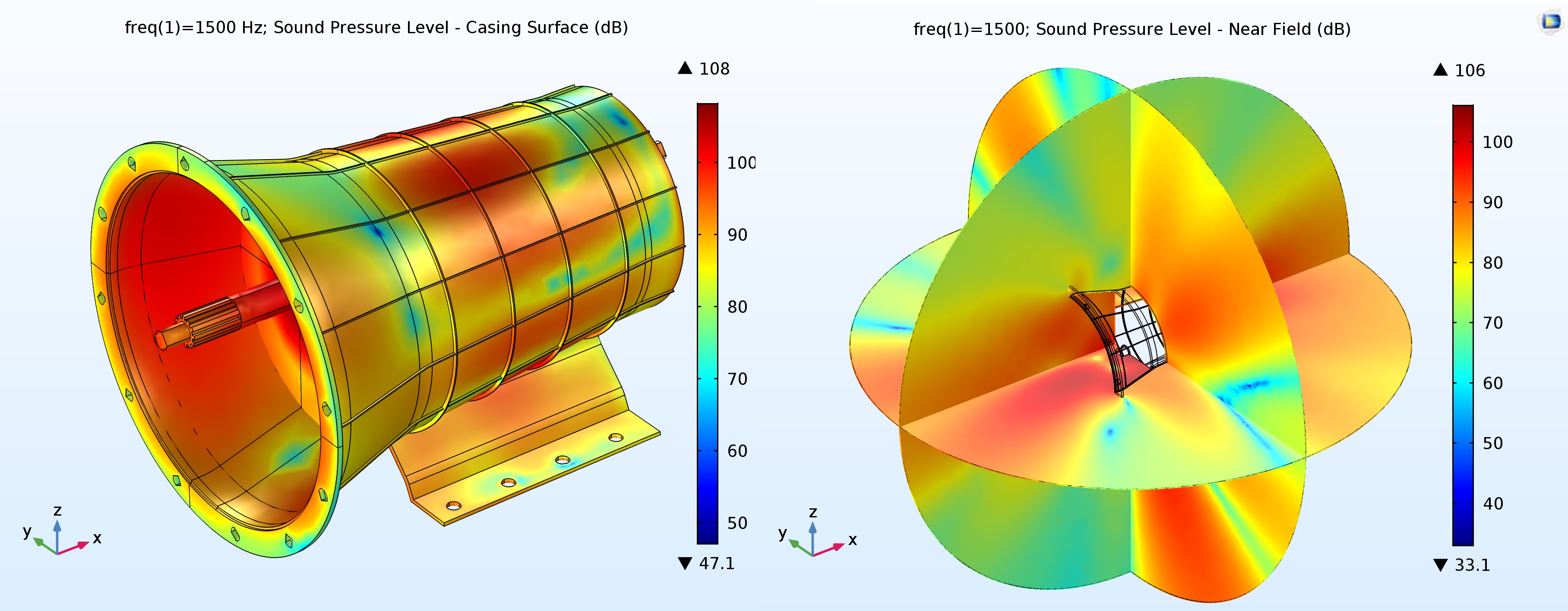
Abb. 4. Schalldruckpegel auf der Gehäuseoberfläche (links) und in der Nahzone (rechts) für eine Frequenz von 1500 Hz.

Abb. 5. Der Schalldruckpegel (dB) in der Fernzone in der xy-, xz- und yz-Ebene in einem Abstand von 1 m für eine Frequenz von 1500 Hz.

Fazit

In diesem Hinweis untersuchten wir eine Methode zur Modellierung von Geräuschen aus einem Getriebe unter Verwendung einer Kombination aus mechanischer statischer Analyse des Getriebes, dynamischer Untersuchung eines Mehrkörpersystems und anschließender akustischer Berechnung.

Mit der tatsächlichen Funktionalität des COMSOL Multiphysics ^® -Pakets können Sie sogar das Geräusch des untersuchten Getriebes im Audioformat aufzeichnen und reproduzieren , wodurch die Simulation einem realen physikalischen Experiment näher kommt.

Diese Technik kann vor Beginn des Produktionsprozesses verwendet werden, um leisere Getriebe im Arbeitsdrehzahlbereich zu erzeugen sowie andere Arbeitsmechanismen in Industrie- und Musikgeräten komplex zu modellieren.

Weitere Informationen

Dieses Material basiert auf folgenden Artikeln:

• Verwenden von Software zur Vorhersage von Getriebegeräuschen , Auto Tech Review, Juni 2017
• So simulieren Sie Vibrationen und Geräusche in einem Getriebe mit COMSOL Multiphysics ^® , COMSOL-Unternehmensblog

Eine ausführliche Videolektion in russischer Sprache über die Montage von Modellen dieser Klasse für die Gelenkschwingung und die akustische Analyse eines Arbeitsgetriebes finden Sie hier . Sie können auch eine Demoversion von COMSOL in den Kommentaren oder auf unserer Website anfordern und sich unabhängig mit dem in diesem Hinweis beschriebenen Modell und den schrittweisen Anweisungen für die Montage vertraut machen.

Weitere Beispiele für die Verwendung von COMSOL ^® in akustischen Berechnungen von Forschungsteams von B & K, Knowles, ABB, HARMAN und der NASA finden Sie in der Ausgabe der COMSOL NEWS 2017: Akustik in russischer Sprache.

Endgültiges GIF: