Dieser Artikel beschreibt die Verwendung der geometrischen Bibliothek von WebGeometry-Funktionen zum Erstellen von Modellen komplexer Polyeder. Die Bibliothek ist in Javascript geschrieben.
Ein Link zu GitHub mit einem Beispiel, das ein einfaches Beispiel für die Verwendung der Bibliothek bietet. Kommentare und Kritik sind willkommen.
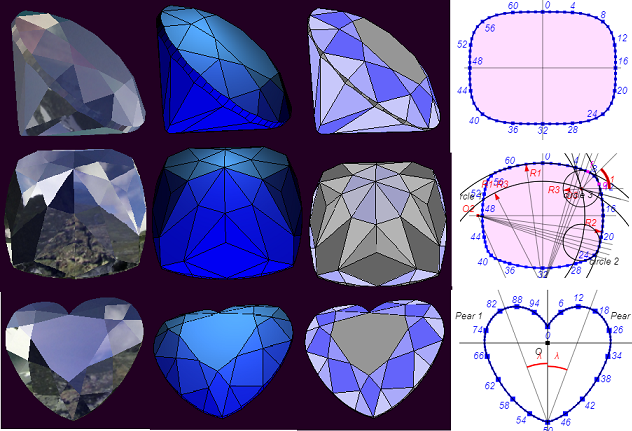
Die ThreeJS-Bibliothek wird verwendet, um Modelle anzuzeigen, die mit Funktionen aus der WebGeometry-Bibliothek vorberechnet wurden. HTML5-Zeichenfläche wird verwendet, um einzelne flache Modellelemente anzuzeigen und unterstützende Informationen anzuzeigen.
WebGL-Technologie und auf dieser Basis erstellte Bibliotheken wie ThreeJS und BadylonJS werden im Internet verwendet, um eine Vielzahl von Zwecken im Zusammenhang mit 3D-Grafiken zu implementieren. Grundsätzlich werden sie jedoch verwendet, um vorgefertigte dreidimensionale Modelle in einem Browser anzuzeigen (zuvor erstellt, z. B. in
3ds Max- oder
Blender- Programmen). Wenn wir vor der Aufgabe stehen, ein parametrisches Modell zu erstellen, dh ein Modell, für das wir beim Anzeigen eines fertigen Objekts im Browser seine einzelnen Elemente ändern können, indem wir die entsprechenden Modellparameter festlegen (z. B. den Winkel eines bestimmten Gesichts vergrößern), die wir benötigen Eine Reihe von geometrischen Funktionen, mit denen Sie ein Modell erstellen können, sodass in Zukunft die Möglichkeit besteht, die Form einzelner Elemente des Modells oder des gesamten Modells interaktiv zu variieren. Um dieses Problem zu lösen, benötigen wir eine Reihe von Funktionen in der Javascript-Sprache, die die in der analytischen Geometrie verwendeten Methoden implementieren. Die Bibliothek muss über Funktionen zum Erstellen von Linien, Ebenen und Kreisen, zum Suchen von Punkten (oder Linien) ihres Schnittpunkts, zum Erstellen von geneigten Ebenen und vielem mehr verfügen. ThreeJS- und BadylonJS-Bibliotheken verfügen über einige dieser Funktionen. Aufgrund der Anzahl der mit ihnen ausgeführten Aktionen können Sie jedoch nicht alle Aufgaben ausführen, die beim Erstellen eines parametrischen Modells auftreten. Es gibt mehrere rein mathematische Javascript-Bibliotheken. Von diesen sind
glMatrix und
Sylvester am weitesten verbreitet. Die
glMatrix- Bibliothek ist hauptsächlich für die Arbeit mit Vektoren, Matrizen und Quaternionen vorgesehen, es gibt jedoch keine Funktionen für die Arbeit mit Linien und Ebenen. Die
Sylvester- Bibliothek verfügt über diese Funktionen, sie sind jedoch nur in begrenztem Umfang vorhanden. Es gibt jedoch mehrere Bücher, die die Implementierung analytischer Geometriemethoden in C / C ++ beschreiben. Entsprechende C / C ++ - Programme können als Prototypen zum Erstellen einer mathematischen Bibliothek in Javascript verwendet werden. Als ich mich entschied, dreidimensionale parametrische Modelle von Diamantschnitten zu erstellen, um sie in einem Browser anzuzeigen, wurde die ThreeJS-Bibliothek von mir nur ausgewählt, um bereits berechnete Modelle anzuzeigen - sie wurde nicht zur Berechnung der Form der Modelle verwendet. Für die Berechnung des Formulars selbst wurde die WebGeometry-Bibliothek erstellt. Diese Bibliothek basierte auf den zuvor verwendeten geometrischen Funktionen in C / C ++, die ich in die Javascript-Sprache übersetzt habe. Betrachten wir die Phasen des Aufbaus eines Pyramidenmodells (Diamantschneiden vom Typ Pyramide).
In der
ersten Phase müssen wir die beabsichtigte Ansicht des Modells zeichnen und dann seine Eckpunkte nummerieren. Die folgende Abbildung zeigt die Nummerierung der Eckpunkte und die Namen der Schnittelemente, die im Pyramidenschnittmodell enthalten sind.

Danach müssen Flächen aus den nummerierten Eckpunkten gebildet werden. Schreiben Sie beispielsweise für das Gesicht der Stelle und die Gesichter der Krone die folgende Folge von Scheitelpunkten (der duplizierte erste Scheitelpunkt des Gesichts signalisiert, dass das Gesicht beendet wurde):
0, 3, 2, 1, 0;
Gesichter sollten gegen den Uhrzeigersinn sein. Die Datei pyramid_index.js enthält den Quellcode zum Durchlaufen aller Flächen der Pyramide sowie detaillierte Kommentare. Das Ergebnis des Crawls wird in das Array index_cut geschrieben.
In der
zweiten Phase können wir die Gesichter des Modells einfärben. Dieser Schritt ist optional, wenn wir keine Färbung benötigen. Angenommen, wir möchten ein Pyramidenmodell wie folgt kolorieren:
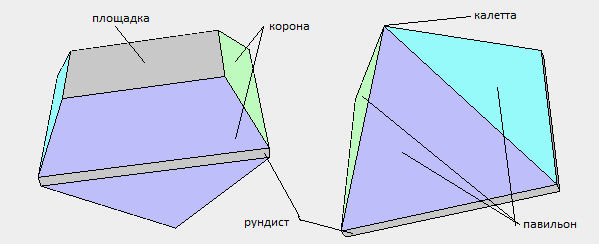
Zu diesem Zweck wird die Datei pyramid_colors.js erstellt, in der sich die Funktion facet_colors () befindet, die die Farben aller Flächen in das Farbarray schreibt.
In der
dritten Stufe müssen nach der Nummerierung aller Scheitelpunkte und der Aufzeichnung der Durchlaufsequenzen aller Scheitelpunkte der Flächen die Modellparameter festgelegt und anschließend die Koordinaten aller Scheitelpunkte berechnet werden. Natürlich wird davon ausgegangen, dass wir den Konstruktionsalgorithmus bereits für uns selbst skizziert und herausgefunden haben, wie sich alle Flächen des Modells im Raum befinden werden. Für die Pyramide wählen wir die folgenden Parameter aus, die die Größe ihrer einzelnen Teile und des gesamten Modells als Ganzes bestimmen:
var DEGREE = 0.01745329251994;
Die Auswahl der Parameter wird vom Entwickler des Modells festgelegt. Anstatt beispielsweise zwei Parameter für zwei Neigungswinkel der Krone festzulegen, können Sie einen einzelnen Parameter für zwei Winkel gleichzeitig angeben. Diese Winkel sind dann immer gleich. Sie können einen Parameter eingeben, der die Größe der Site bestimmt. In diesem Fall ist es erforderlich, entweder die Kronenhöhe oder die Neigung seiner Flächen nicht einzustellen. Eine weitere Option zur Auswahl von Parametern besteht darin, einige Parameter berechenbar zu machen. In diesem Fall können beim Ändern einiger Parameter andere ihren Anfangswert ändern. Wenn wir beispielsweise annehmen, dass wir für die Pyramide einen Parameter zum Einstellen des Neigungswinkels der koronalen Flächen, einen anderen Parameter für die Höhe der Krone und einen anderen Parameter zum Festlegen der Größe der Fläche definiert haben, müssen wir beim Ändern des Winkels der Flächen entweder die Größe der Fläche oder ändern Kronenhöhe. Wenn Sie dagegen den Parameter ändern, mit dem die Größe des Pads festgelegt wird, ändert sich automatisch der Wert des Parameters, mit dem entweder die Höhe oder die Neigung der koronalen Flächen festgelegt wird. Die Option, die mit der Anwendung der berechneten Parameter in diesem Programm sowie mit der Konstruktion der anderen auf der Website vorgestellten Schnittmodelle verbunden ist, wird nicht verwendet.
In der
vierten Stufe werden die Koordinaten der Modellscheitelpunkte berechnet. Die anfänglichen Daten für die Berechnung sind die Werte der Modellparameter und wie wir uns deren Aussehen vorstellen. Die Datei pyramid_verts.js enthält den Quelltext (mit detaillierten Kommentaren) der Scheitelpunktberechnungsfunktion des Modells, die als VerticesCalculation bezeichnet wird. Bei dieser Berechnung werden die Funktionen der WebGeometry-Bibliothek in dieser Funktion verwendet. Die Ergebnisse der Berechnung der Koordinaten der Scheitelpunkte werden in das Scheitelpunktarray eingegeben. Beachten Sie, dass im Programm zum Ermitteln der Koordinaten der Scheitelpunkte separate Zahlenfolgen für die Scheitelpunkte verwendet werden, aus denen die Korona (vier Scheitelpunkte), die Scheitelpunkte des Gürtels (vier Scheitelpunkte) und die Scheitelpunkte des Pavillons bestehen (im Pyramidenmodell ist nur der Scheitelpunkt im Pavillon enthalten). Diese Wahl der zusätzlichen Scheitelpunktnummerierung wird vom Programmierer zur leichteren Orientierung zwischen den geschnittenen Scheitelpunkten verwendet, da die Anzahl der Scheitelpunkte sehr oft 100 überschreitet.
In der
fünften Stufe, nachdem die Berechnung der Koordinaten der Eckpunkte abgeschlossen ist, muss das Polyeder (Polyeder) des Modells programmgesteuert konstruiert werden. Die anfänglichen Daten für seine Konstruktion sind zuvor erstellte Arrays aus index_cut, Farben und Eckpunkten. Ein Polyedermodell kann einfach als eine Reihe von Flächen dargestellt werden, die ein Polyeder im Raum begrenzen. Die CreatePolyhedron-Funktion befindet sich in der Datei polyhedron.js. Als Ergebnis der Arbeit dieser Funktion wird ein Array von Polygonen (Polygonen) erstellt, aus denen das dreidimensionale Modell besteht. Jedes Polygon wird durch die folgende Funktion beschrieben (tatsächlich ist es eine Konstruktorfunktion, die vom neuen Operator beim Erstellen eines neuen Polygons aufgerufen wird):
function Polygon() { this.IndexFacet = [];
Da WebGL und die auf ihrer Basis erstellte ThreeJS-Bibliothek mit dreieckigen Grundelementen arbeiten, wird sie für jede Fläche des Modells trianguliert. Es wird angenommen, dass alle Flächen des Modells konvexe Polygone sind. Letztendlich führt die CreatePolyhedron-Funktion alle erforderlichen Schritte aus, um Datenstrukturen zu erstellen, die alle Flächen des Polyeders vollständig beschreiben, sodass sie an die ThreeJS-Bibliotheksfunktionen übergeben werden können, um das Modell auf dem Bildschirm anzuzeigen.
In der
sechsten Stufe wird das Modell mit den ThreeJS-Funktionen auf dem Bildschirm angezeigt. Standardmäßig werden Szene, Renderer und Kamera erstellt. Um das Schnittmodell von allen Seiten zu untersuchen, verwendet das Pyramid-Programm das Element orbitControls. Beim Erstellen anderer Schnittmodelle habe ich keine orbitControls verwendet, um Schnitte von allen Seiten zu untersuchen, sondern die Möglichkeit eingeführt, das Modell selbst zu drehen. Dann erstellen wir die Modellnetze. Sie können zwei Dinge tun.
Bei der ersten Methode betrachten wir das Schnittmodell als einen Satz separater Flächennetze. In diesem Fall ist jedes Gesicht ein separates 3D-Objekt. Mit dieser Darstellung des Modells ist die Auswahl eines einzelnen Gesichts mithilfe des Three.JS-Elements mit dem Namen raycaster recht einfach. Diese Methode kann auch durch die Erstellung von Maschen von Segmenten ergänzt werden, die an jede Fläche angrenzen.
Auf die zweite Weise betrachten wir das Schnittmodell als ein einzelnes Objekt, das durch nur ein Netz dargestellt wird, das sofort alle Flächen des Modells enthält. Diese Methode ist praktisch, wenn Sie ein Modell mit Shadern anzeigen. Diese Methode wird im Pyramid-Schnittmodell nicht verwendet, aber sie wird verwendet, um Octagon-, Brilliant- und andere Schnittmodelle zu erstellen, die auf meiner Website zu sehen sind.
In der
siebten Phase werden Schaltflächen und Funktionen erstellt, mit denen Sie den Wert der Parameter ändern können, die die Form und Größe des Modells bestimmen. Wenn eine Taste gedrückt wird, wird eine Funktion aufgerufen, die den Wert des entsprechenden Parameters erhöht oder verringert. Dies bedeutet, dass der Wert der Koordinaten der Eckpunkte des Modells neu berechnet werden muss. Nach dem Nachzählen wird die Richtigkeit des neu konstruierten Modells überprüft. Beispielsweise wird festgestellt, ob einige Werte außerhalb der Toleranz liegen. Bei Modellen mit Diamantschliff kommt es normalerweise darauf an, zu prüfen, ob der konvexe Schliff nach dem Wiederaufbau erhalten bleibt. Überprüfen Sie die Ausbuchtung wie folgt. Durch jede Fläche wird eine Ebene gezeichnet, in der diese Fläche liegt, und dann wird die Position jedes Scheitelpunkts des Modells relativ zu dieser Ebene bestimmt. Alle Eckpunkte sollten sich auf derselben Seite dieser Ebene befinden. Wenn das Modell als falsch angesehen wird, wird der Parameter auf seinen ursprünglichen Wert zurückgesetzt und das Modell erneut erstellt. Bei Schnittmodellen mit einem nicht konvexen Gürtel (nur dieses Element einiger Schnitte, wie z. B. Herz, kann nicht konvex sein) wird die Konvexität separat für die Krone und separat für den Pavillon geprüft. Der Rundist ist jedoch von der Prüfung ausgeschlossen. Bei einfachen Modellen können Sie sich auf eine einfache Parameterprüfung beschränken. Wenn wir beispielsweise ein Modell eines Hauses bauen, sollte das Dach im Voraus nicht höher als eine bestimmte Höhe sein. Wenn Sie also einfach die Größenbeschränkung dieses Parameters einstellen, erhalten Sie das gewünschte Ergebnis. Nach dem Hinzufügen der Parameterschaltflächen ist es sehr wünschenswert, den Wert jedes Parameters visuell anzuzeigen, wenn er sich nach dem Klicken auf die Schaltfläche ändert. Dazu wird eine zweidimensionale HTML5-Zeichenfläche erstellt und neben der entsprechenden Schaltfläche der Parameterwert angezeigt.
Daher haben wir alle Phasen des Modellbaus am Beispiel der Pyramide untersucht. Für die Pyramide (sowie für alle anderen Modelle auf der Site) habe ich ein weiteres Programm Pyramid_text.html erstellt. Das Beispiel dieses Programms zeigt, wie Sie dreidimensionalen Text zur Nummerierung der Eckpunkte eines Modells anzeigen können. Wenn jemand wissen möchte, wie komplexe Modelle erstellt werden, sollten Sie Modelle
(siehe GitHub) in der folgenden Reihenfolge erstellen:
Achteck . Ein Modell, das die Erstellung von Ebenen auf verschiedene Weise demonstriert und mit diesen Ebenen arbeitet. Bei der Erstellung eines Modells werden auch Methoden verwendet, die beim Arbeiten mit Vektoren und Linien im Raum verwendet werden.
Genial . Dies ist der klassische und gebräuchlichste Diamantschliff. Einige Elemente zur Erstellung eines dreidimensionalen Modells dieses Schnitts werden in Zukunft beim Erstellen von Facetten MoonMarquise, MoonPear und Heart verwendet. Wie der Gürtel dieses Schnitts, der die Form einer Superellipse hat, berechnet wird, wird im Programm BrilliantGirdlt.html separat angezeigt. In diesem Programm wird die Gürtellinie auf einer zweidimensionalen Leinwand (Leinwand) aufgebaut.
MoonMarquise . Der Marquise-Schliff ist wie Brilliant einer der klassischen Diamantschliffe. Im Gegensatz zu einer einfachen Facette dieses Typs (Marquise) werden der MoonMarquise-Facette des Pavillons die sogenannten „Mondfacetten“ hinzugefügt. Der MoonMarquise-Cutter besteht aus zwei Ellipsenbögen. Eine detaillierte Konstruktion dieses Gürtels auf Leinwand wird im Programm MarquiseGirdle.html gezeigt. Der Text dieses Programms enthält detaillierte Kommentare zum Aufbau. Wir stellen einen Punkt in Bezug auf die Berechnung der Gürtellinie fest - sie verwendet die Eigenschaft einer Tangente an eine Ellipse. Es wird zum Beispiel in dem Buch "Course of Analytical Geometry" (der Autor dieses Buches ist N. I. Muskhelishvili) betrachtet.
MoonPear Der MoonPear-Zackenbarsch besteht aus den Bögen von drei Ellipsen. Seine Konstruktion basiert auf der Konstruktion des Marquise-Gürtels, ist jedoch komplexer. Führen Sie das Programm PearGirdle.html aus, um die Marquise-Gürtellinie zu sehen und zu erfahren, wie Sie den Gundist in Segmente aufteilen.
Herz Der "Herz" -Schnitt ist einer der klassischen Schnitte, hat jedoch im Gegensatz zu den meisten Arten von Schnitten eine nicht konvexe Gürtelform. Der Herzschnitt-Rudist besteht aus zwei Birnenschliffgürteln, die relativ zueinander geneigt sind. Auf der Leinwand können Sie die Gürtellinie sehen, indem Sie das Programm HeartGirdle.html ausführen. Einen Herzschnitt zu bauen ist eine ziemliche Herausforderung.
Malteserkreuz . Der Cutter des geschnittenen „Malteserkreuzes“ besteht aus einem „Kissen“ (Kissen). Stecklinge mit einem solchen Gürtel sind in letzter Zeit weit verbreitet. Die Linie dieses Gürtels besteht aus acht konjugierten Kreisbögen - vier Hauptbögen, die an vier Seiten an das Kissen angrenzen, und vier Bögen kleinerer Größe, die die Hauptbögen des Kissens an den Ecken des Gürtels paaren. Durch Ausführen der Programme CushionGirdle_1.html und CushionGirdle_2.html können Sie die Form der Linie des Gürtels, die Arbeit aller Parameter, die seine Form definieren, und die Aufteilung des Gürtels in Segmente sehen.
Fünfeckiger Stern . Der fünfeckige Sternschneider wird durch eine Linie gebildet, die den Namen des Epitrochoids trägt. Das Epitrochoid ist eine Kurve, die sich auf die Zykloide bezieht. Im Programm Wavy_Pentagon_Girdle.html können Sie durch Ändern der Parameterwerte die „Welligkeit“ des Gürtels und sogar das Fünfeck in ein Polygon mit einer anderen Anzahl von Vorsprüngen („Blütenblätter“) ändern. Es ist jedoch zu beachten, dass das Modell dieses Schnitts selbst für den Wert des Parameters „Anzahl der Blütenblätter“ von 5 erstellt wurde.
Wie bereits erwähnt, werden für alle oben genannten Modelle Programme erstellt, die die Anzahl der geschnittenen Scheitelpunkte anzeigen. In diesen Programmen wird zwischen der Durchgangsanzeige aller Scheitelpunkte des Modells und der getrennten Anzeige der Scheitelpunktnummern für Krone, Gürtel und Pavillon umgeschaltet. Angenommen, Sie möchten im maltesischen Schnittmodell eine Ebene erstellen, die durch die Scheitelpunkte mit den Nummern 84, 88 und 145 verläuft. Anstatt diese Zahlen zu verwenden, um die Punkte zu identifizieren, durch die die Ebene beim Erstellen einer Ebene mit der Funktion CreatePlaneThreePoints verläuft, wird eine Aufzeichnung mit einer separaten Funktion erstellt Nummerierung der Gipfel für Gürtel und Pavillon:
var plane = new Plane3D(); plane.CreatePlaneThreePoints(girdle[68], girdle[72], crown[1]);
Es ist zu beachten, dass Programme, die Modellscheitelpunktnummern anzeigen, sehr langsam arbeiten (zumindest auf meinem Computer). Es kann einige Sekunden dauern, bis die Ausgabe der Modellscheitelpunktnummern abgeschlossen ist.
Um all das zusammenzufassen, ist meiner Meinung nach die Wahl von Polyedern (Schnittmodellen) zur Demonstration der Funktionsweise geometrischer Funktionen eine der besten Optionen. Nachdem wir die Arbeit der obigen Beispiele untersucht haben, können wir mit der Erstellung geometrischer Objekte fortfahren, die sich auf völlig andere Tätigkeitsfelder beziehen als die Modellierung des Diamantschneidens.