Numerische Lösung mathematischer Modelle von Objekten, die durch Differentialgleichungssysteme gegeben sind

Einführung:

Bei der mathematischen Modellierung einer Reihe technischer Geräte werden Systeme nichtlinearer Differentialgleichungen verwendet. Solche Modelle werden nicht nur in der Technologie verwendet, sondern auch in den Bereichen Wirtschaft, Chemie, Biologie, Medizin und Management.

Die Untersuchung der Funktionsweise solcher Geräte erfordert die Lösung dieser Gleichungssysteme. Da der Großteil solcher Gleichungen nichtlinear und nicht stationär ist, ist es oft unmöglich, ihre analytische Lösung zu erhalten.

Es müssen numerische Methoden verwendet werden, von denen die bekannteste die Runge-Kutta-Methode ist [1]. Was Python betrifft, so gibt es in Veröffentlichungen zu numerischen Methoden, zum Beispiel [2,3], nur sehr wenige Daten zur Verwendung von Runge-Kutta, und es gibt keine Daten zu seiner Modifikation der Runge-Kutta-Felberg-Methode.

Derzeit hat die Odeint-Funktion des Moduls scipy.integrate dank ihrer einfachen Oberfläche die größte Verbreitung in Python. Die zweite Funktions-Ode dieses Moduls implementiert mehrere Methoden, einschließlich der erwähnten fünfrangigen Runge-Kutta-Felberg-Methode, weist jedoch aufgrund ihrer Universalität eine begrenzte Leistung auf.

Der Zweck dieser Veröffentlichung ist eine vergleichende Analyse der aufgelisteten Mittel zum numerischen Lösen von Differentialgleichungssystemen mit einem modifizierten Autor unter Python unter Verwendung der Runge-Kutta-Felberg-Methode. Die Veröffentlichung bietet auch Lösungen für Randwertprobleme für Differentialgleichungssysteme (SDEs).

Kurze theoretische und tatsächliche Daten zu den betrachteten Methoden und Software für die numerische Lösung von CDS

Cauchys Problem

Für eine Differentialgleichung n-ter Ordnung besteht das Cauchy-Problem darin, eine Funktion zu finden, die die Gleichheit erfüllt:



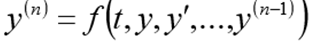
und Anfangsbedingungen



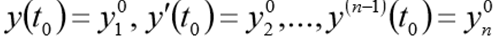
Bevor Sie dieses Problem lösen, sollten Sie es in Form der folgenden CDS umschreiben

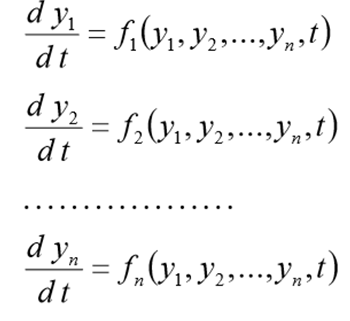
(1)

mit Anfangsbedingungen



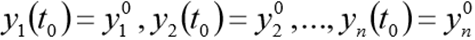Scipy.integrate-Modul

Das Modul hat zwei Funktionen ode () und odeint (), mit denen Systeme gewöhnlicher Differentialgleichungen (ODEs) erster Ordnung mit Anfangsbedingungen an einem Punkt gelöst werden können (Cauchy-Problem). Die Funktion ode () ist universeller und die Funktion odeint () (ODE-Integrator) hat eine einfachere Schnittstelle und löst die meisten Probleme gut.

Odeint () Funktion

Die Funktion odeint () verfügt über drei erforderliche Argumente und viele Optionen. Es hat das folgende Format odeint (func, y0, t [, args = (), ...]) Das Argument func ist der Python-Name der Funktion zweier Variablen, von denen die erste die Liste y = [y1, y2, ..., yn ist ] und der zweite ist der Name der unabhängigen Variablen.

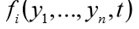
Die Funktion func sollte eine Liste von n Funktionswerten zurückgeben für einen gegebenen Wert des unabhängigen Arguments t. Tatsächlich implementiert die Funktion func (y, t) die Berechnung der rechten Seiten des Systems (1).

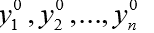
Das zweite Argument y0 von odeint () ist ein Array (oder eine Liste) von Anfangswerten bei t = t0.

Das dritte Argument ist eine Reihe von Zeitpunkten, zu denen Sie eine Lösung für das Problem erhalten möchten. In diesem Fall wird das erste Element dieses Arrays als t0 betrachtet.

Die Funktion odeint () gibt ein Array der Größe len (t) x len (y0) zurück. Die Funktion odeint () verfügt über viele Optionen, die den Betrieb steuern. Die Optionen rtol (relativer Fehler) und atol (absoluter Fehler) bestimmen den Berechnungsfehler ei für jeden Wert von yi gemäß der Formel



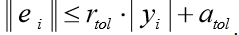
Sie können Vektoren oder Skalare sein. Default



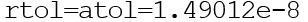Ode () Funktion

Die zweite Funktion des Moduls scipy.integrate, mit dem Differentialgleichungen und -systeme gelöst werden sollen, heißt ode (). Es wird ein ODE-Objekt erstellt (Typ scipy.integrate._ode.ode). Wenn man eine Verknüpfung zu einem solchen Objekt hat, sollte man seine Methoden verwenden, um Differentialgleichungen zu lösen. Ähnlich wie bei der Funktion odeint () reduziert die Funktion ode (func) das Problem auf ein System von Differentialgleichungen der Form (1) und verwendet dessen Funktion auf der rechten Seite.

Der einzige Unterschied besteht darin, dass die Funktion der rechten Funktion (t, y) eine unabhängige Variable als erstes Argument und die Liste der Werte der gewünschten Funktionen als zweites Argument akzeptiert. Mit der folgenden Befehlsfolge wird beispielsweise eine ODE erstellt, die eine Cauchy-Aufgabe darstellt.

Runge-Kutta-Methode

Bei der Konstruktion numerischer Algorithmen wird davon ausgegangen, dass es eine Lösung für dieses Differentialproblem gibt, die eindeutig ist und die erforderlichen Glätteigenschaften aufweist.

In der numerischen Lösung des Cauchy-Problems

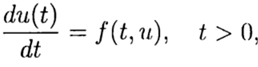
(2)

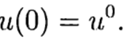
(3)

gemäß der bekannten Lösung am Punkt t = 0 ist es notwendig, eine Lösung aus Gleichung (3) für andere t zu finden. In der numerischen Lösung von Problem (2), (3) verwenden wir der Einfachheit halber ein einheitliches Gitter in der Variablen t mit einem Schritt t> 0.

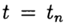
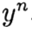
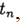
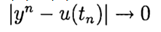
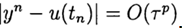
Eine ungefähre Lösung für Problem (2), (3) am Punkt bezeichnen . Methode konvergiert an einem Punkt wenn bei . Die Methode hat eine p-te Genauigkeitsordnung, wenn , p> 0 für . Das einfachste Differenzschema für eine ungefähre Lösung des Problems (2), (3) ist

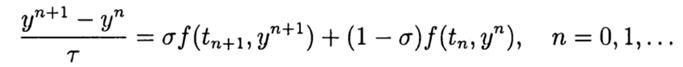
(4)

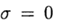
Bei Wir haben eine explizite Methode und in diesem Fall nähert sich das Differenzschema Gleichung (2) mit der ersten Ordnung an. Symmetrisches Design in (4) hat eine zweite Näherungsordnung. Dieses Schema gehört zur Klasse der impliziten - um die ungefähre Lösung auf einer neuen Ebene zu bestimmen, muss das nichtlineare Problem gelöst werden.

Es ist zweckmäßig, explizite Approximationsschemata zweiter und höherer Ordnung basierend auf der Prädiktor-Korrektor-Methode zu konstruieren. In der Phase des Prädiktors (Vorhersage) wird ein explizites Schema verwendet.

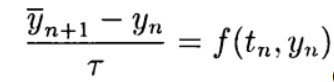
(5)

und in der Korrekturphase (Verfeinerung) ein Diagramm



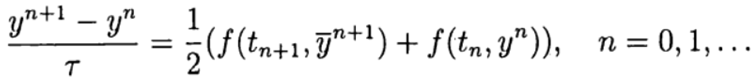
Bei den einstufigen Runge-Kutta-Methoden werden die Ideen des Prädiktor-Korrektors am vollständigsten umgesetzt. Diese Methode ist in allgemeiner Form geschrieben:

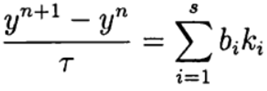
(6)

wo



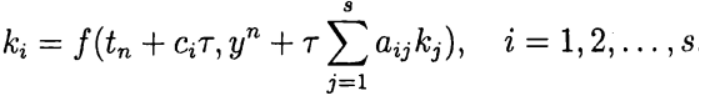
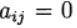
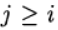
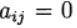
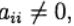
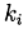
Die Formel (6) basiert auf s Berechnungen der Funktion f und wird als s-Stufe bezeichnet. Wenn bei Wir haben die explizite Runge-Kutta-Methode. Wenn für j> 1 und dann implizit aus der Gleichung bestimmt:

(7)

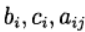
Diese Runge-Kutta-Methode wird als diagonal implizit bezeichnet. Parameter Bestimmen Sie eine Variante der Runge-Kutta-Methode. Die folgende Darstellung der Methode wird verwendet (Butcher-Tabelle)



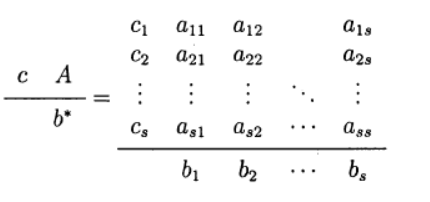
Eine der häufigsten ist die explizite Runge-Kutta-Methode vierter Ordnung.

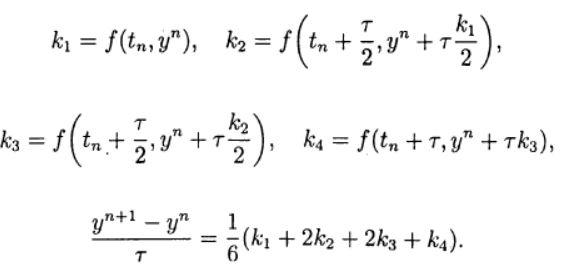
(8)

Runge-Kutta-Felberg-Methode

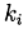
Ich gebe den Wert der berechneten Koeffizienten an Methode

(9)

In Anbetracht von (9) hat die allgemeine Lösung die Form:

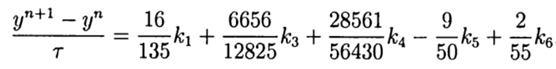
(10)

Diese Lösung bietet die fünfte Genauigkeitsordnung, die noch an Python angepasst werden muss.

Computerexperiment zur Bestimmung des absoluten Fehlers der numerischen Lösung einer nichtlinearen Differentialgleichung 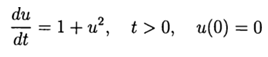Verwenden Sie sowohl die Funktionen def odein () als auch def oden () des Moduls scipy.integrate und die an Python angepassten Methoden Runge-Kutta und Runge-Kutta-Felberg

Wir bekommen:









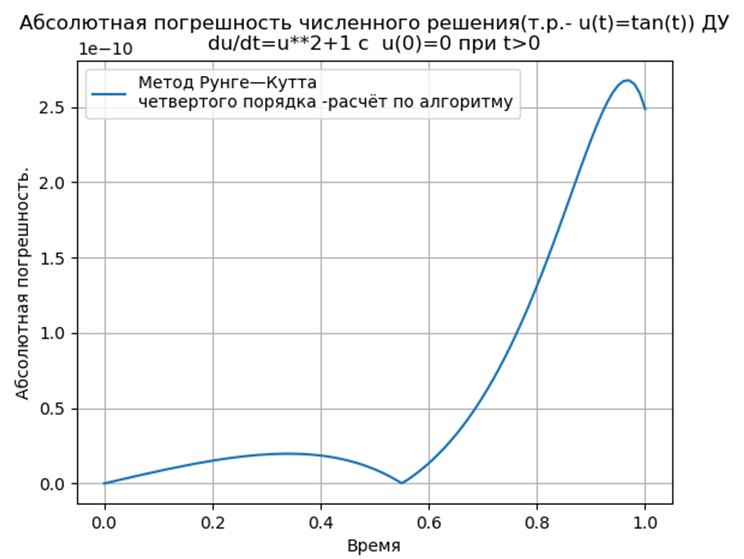
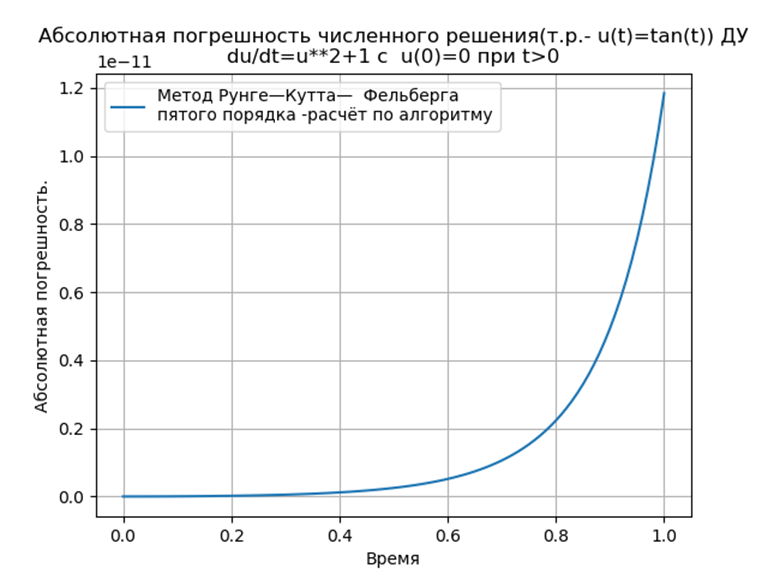
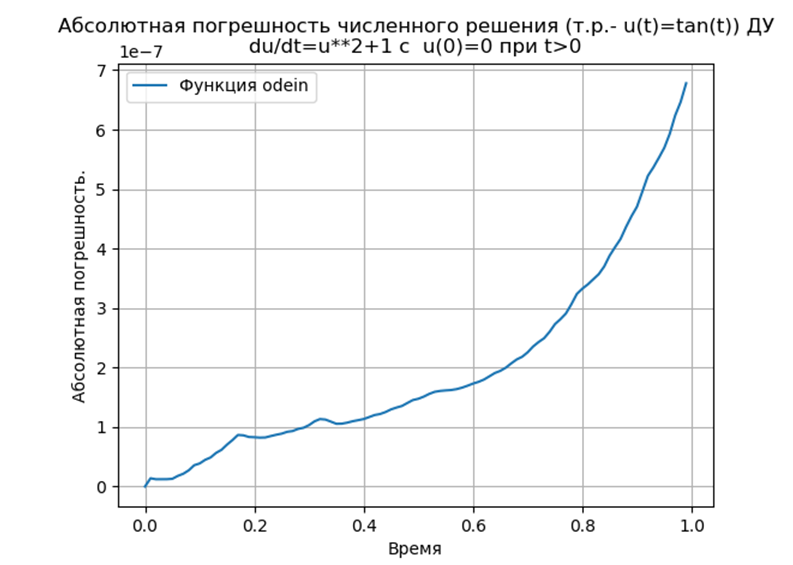
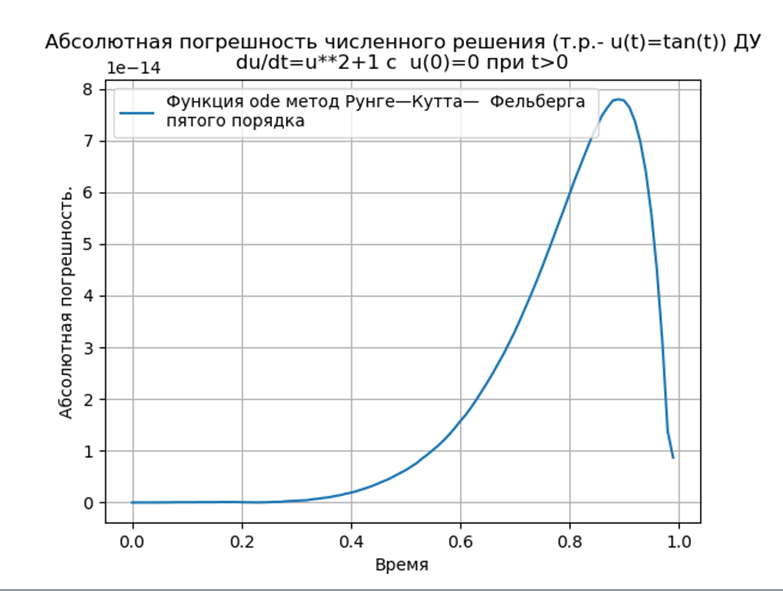Fazit:

Python-angepasste Runge-Kutta- und Runge-Kutta-Felberg-Methoden haben ein niedrigeres Absolut als eine Lösung mit der Odeint-Funktion, aber mehr als eine Lösung mit der Edu-Funktion. Es ist notwendig, eine Leistungsstudie durchzuführen.

Ein numerisches Experiment zum Vergleich der Geschwindigkeit der numerischen Lösung von SDEs unter Verwendung der Ode-Funktion mit dem Attribut dopri5 (Runge-Kutta-Methode 5. Ordnung) und unter Verwendung der an Python angepassten Runge-Kutta-Felberg-Methode

Eine vergleichende Analyse wird am Beispiel des in [2] angegebenen Modellproblems durchgeführt. Um die Quelle nicht zu wiederholen, werde ich die Formulierung und Lösung des Modellproblems aus [2] vorstellen.

Lösen wir das Cauchy-Problem, das die Bewegung eines Körpers beschreibt, der mit einer Anfangsgeschwindigkeit v0 in einem Winkel α zum Horizont geworfen wird, unter der Annahme, dass der Luftwiderstand proportional zum Quadrat der Geschwindigkeit ist. In Vektorform hat die Bewegungsgleichung die Form



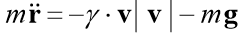
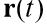
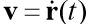
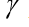
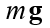
wo Ist der Radius des Vektors des sich bewegenden Körpers, Ist der Geschwindigkeitsvektor des Körpers, - Widerstandsbeiwert, Vektor Kräfte des Körpergewichts der Masse m, g - Erdbeschleunigung.



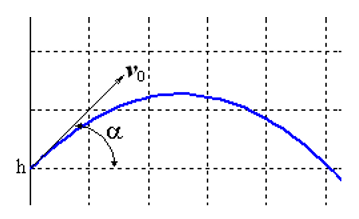
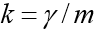
Die Besonderheit dieser Aufgabe ist, dass die Bewegung zu einem zuvor unbekannten Zeitpunkt endet, wenn der Körper zu Boden fällt. Wenn angegeben , dann haben wir in Koordinatenform ein Gleichungssystem:



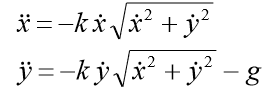
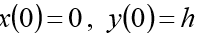
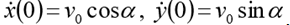
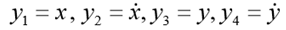
Die Anfangsbedingungen sollten dem System hinzugefügt werden: (h Anfangshöhe) . Put . Dann nimmt das entsprechende ODE-System erster Ordnung die Form an:



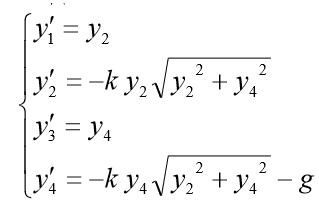
Für das Modellproblem setzen wir . Wenn ich eine ziemlich ausführliche Beschreibung des Programms weglasse, werde ich nur eine Auflistung der Kommentare geben, zu denen meines Erachtens das Prinzip seiner Funktionsweise klar sein wird. Das Programm hat einen Countdown für die vergleichende Analyse hinzugefügt.



Wir bekommen:

Flugzeit = 1,2316 Entfernung = 5,9829 Höhe = 1,8542
Flugzeit = 1.1016 Entfernung = 4.3830 Höhe = 1.5088
Flugzeit = 1.0197 Entfernung = 3.5265 Höhe = 1.2912
Flugzeit = 0,9068 Entfernung = 2,5842 Höhe = 1,0240
Zeit für Modellproblem: 0,454787



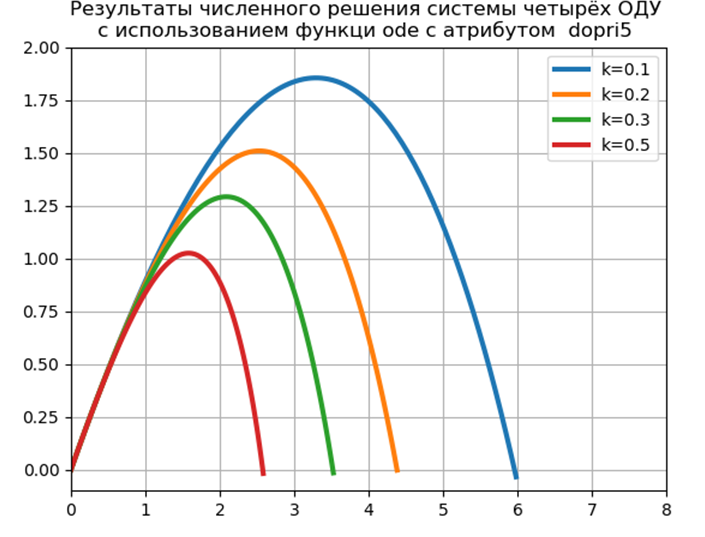
Um eine numerische Lösung des CDS mit Python-Tools ohne Verwendung spezieller Module zu implementieren, habe ich die folgende Funktion vorgeschlagen und untersucht:

def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6

Die Inkrementfunktion (f, t, y, tau) liefert die fünfte Ordnung der numerischen Lösungsmethode. Weitere Funktionen des Programms finden Sie in der folgenden Liste:


Wir bekommen:

Zeit für Modellproblem: 0,259927



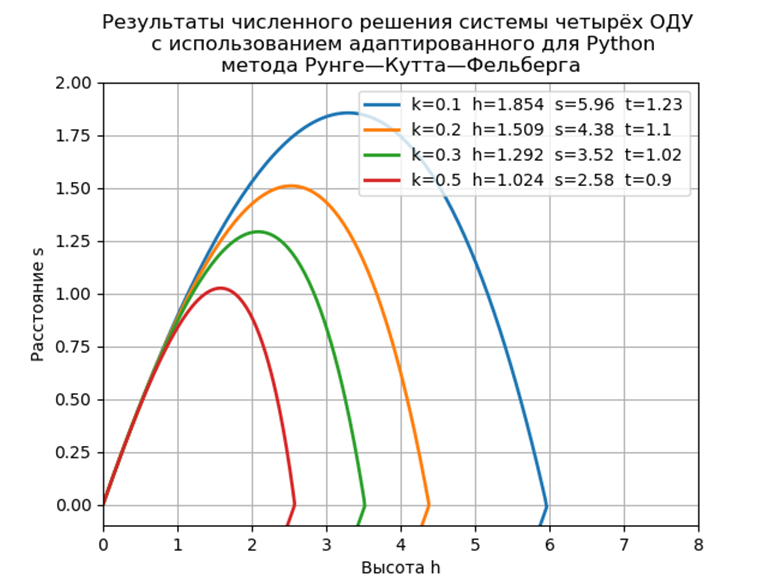Fazit

Die vorgeschlagene Software-Implementierung des Modellproblems ohne Verwendung spezieller Module hat eine fast doppelt so schnelle Leistung wie mit der Ode-Funktion, aber wir dürfen nicht vergessen, dass die Ode eine höhere Genauigkeit der numerischen Lösung und die Möglichkeit der Auswahl einer Lösungsmethode aufweist.

Lösen eines Randwertproblems mit fadengetrennten Randbedingungen

Wir geben ein Beispiel für ein spezifisches Randwertproblem mit fadengetrennten Randbedingungen:

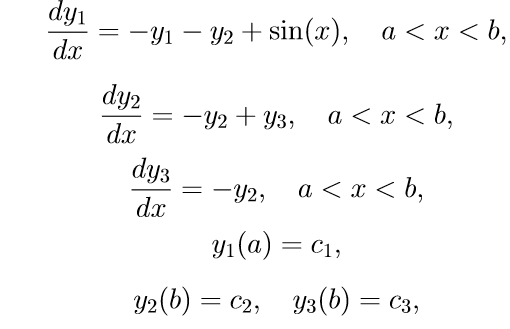
(11)

Um das Problem (11) zu lösen, verwenden wir den folgenden Algorithmus:

1. Wir lösen die ersten drei inhomogenen Gleichungen von System (11) mit den Anfangsbedingungen

Wir führen die Notation zur Lösung des Cauchy-Problems ein:


2. Wir lösen die ersten drei homogenen Gleichungen von System (11) mit den Anfangsbedingungen

Wir führen die Notation zur Lösung des Cauchy-Problems ein:


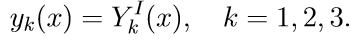
3. Wir lösen die ersten drei homogenen Gleichungen von System (11) mit den Anfangsbedingungen



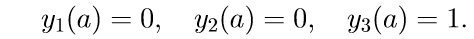
Wir führen die Notation zur Lösung des Cauchy-Problems ein:



4. Die allgemeine Lösung des Randwertproblems (11) unter Verwendung der Lösungen der Cauchy-Probleme wird als lineare Kombination von Lösungen geschrieben:

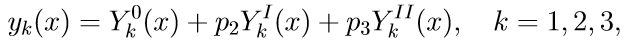
Dabei sind p2, p3 einige unbekannte Parameter.

5. Um die Parameter p2, p3 zu bestimmen, verwenden wir die Randbedingungen der letzten beiden Gleichungen (11), dh die Bedingungen für x = b. Durch Einsetzen erhalten wir ein lineares Gleichungssystem in Bezug auf unbekanntes p2, p3:
(12)
Wenn wir (12) lösen, erhalten wir die Beziehungen für p2, p3.

Unter Verwendung des obigen Algorithmus unter Verwendung der Runge-Kutta-Felberg-Methode erhalten wir das folgende Programm:


Wir bekommen:

y0 [0] = 0,0
y1 [0] = 1,0
y2 [0] = 0,7156448588231397
y3 [0] = 1,324566562303714
y0 [N-1] = 0,9900000000000007
y1 [N-1] = 0,1747719838716767
y2 [N-1] = 0,8
y3 [N-1] = 0,5000000000000001
Zeit für Modellproblem: 0.070878

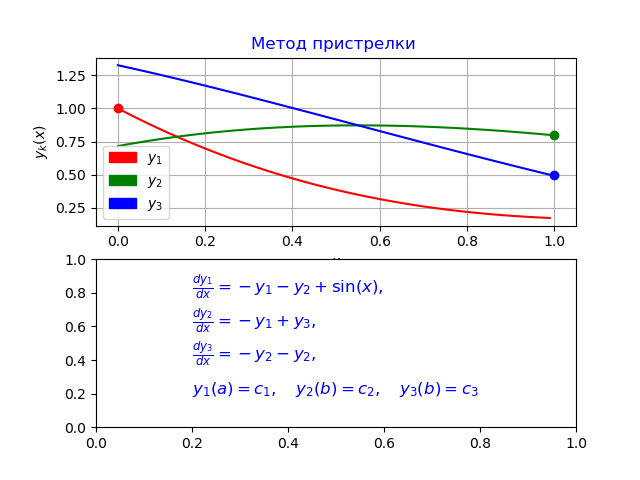
Fazit

Das von mir entwickelte Programm unterscheidet sich von dem in [3] angegebenen Fehler, der die zu Beginn des Artikels angegebene vergleichende Analyse der Odeint-Funktion mit der in Python implementierten Runge-Kutta-Felberg-Methode bestätigt.

Referenzen:

1. Numerische Lösung mathematischer Modelle von Objekten, die durch zusammengesetzte Differentialgleichungssysteme definiert sind.

2. Einführung in das wissenschaftliche Python.

3. N.M. Polyakova, E.V. Shiryaeva Python 3. Erstellen einer grafischen Benutzeroberfläche (am Beispiel der Lösung des Randwertproblems für lineare gewöhnliche Differentialgleichungen mit der Aufnahmemethode). Rostow am Don 2017.