"Manueller" Manipulator

Einmal, während meines zweiten Studienjahres, wurde mir die Aufgabe übertragen, etwas "Art" zu kochen, um den hohen Rang eines "zukünftigen Robotikingenieurs" zu bestätigen. In diesem Pathos ging ich in die Tiefen des Bewusstseins, um nach Ideen zu suchen. Nach einer kurzen Reise entstand eine Idee über das Gerät, dessen Schöpfungstheorie ich der Öffentlichkeit mitteilen möchte.

Das Wesen der Entwicklung ist dies. Betrachten Sie beispielsweise den üblichen 5-Achsen-Manipulator (das kinematische Strukturdiagramm ist in der folgenden Abbildung dargestellt). Seine Fähigkeiten beim Bewegen im Raum sind breit: Er kann Bewegungen in 5 Koordinaten ausführen und gleichzeitig, d.h. 3 Koordinaten entlang der drei XYZ-Achsen und Drehung um zwei von ihnen. In diesem Fall kann das Arbeitselement des Manipulators jede Position im Arbeitsraum einnehmen und gleichzeitig die erforderliche Ausrichtung des Arbeitskörpers beibehalten (ohne Berücksichtigung der Drehung des Arbeitselements um seine eigene Achse).



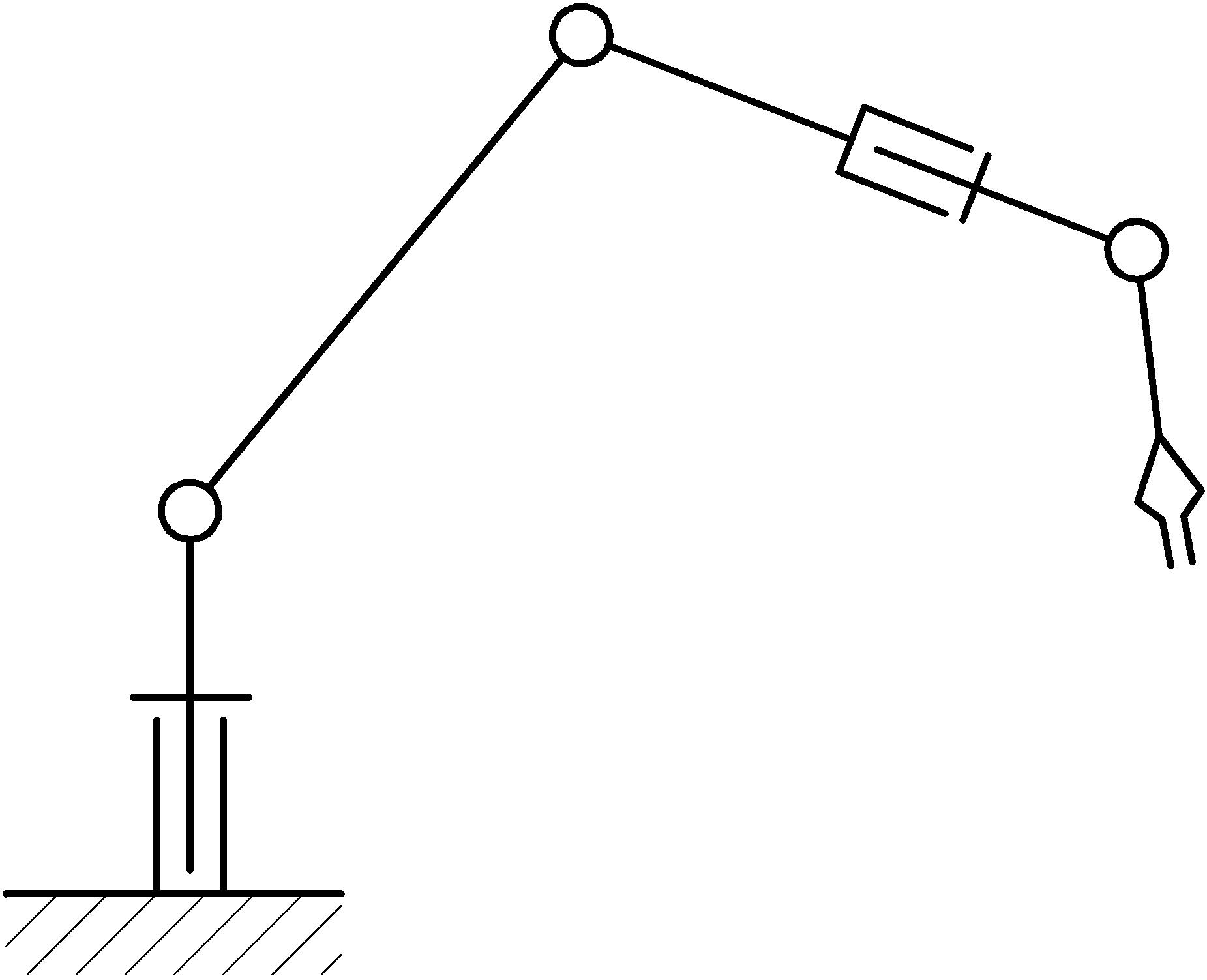
Dieses Design bezieht sich auf Manipulatoren eines anthropomorphen Typs und ist daher in der Lage, ungefähr natürlich die Bewegung einer menschlichen Hand zu reproduzieren. Als ich über diese These stritt, kam mir gerade die Idee, dass es interessant wäre, den Manipulator dazu zu bringen, die Bewegungen meiner Hand in Echtzeit aus der Ferne zu kopieren. Damit ich nur einen Sensor auf meine Hand lege, der die Bewegungen der Hand (sowohl linear als auch eckig) liest, und diese mechanische Sache wird sie nach mir wiederholen. Da der Manipulator die Funktionen des Bewegens und Orientierens des Arbeitskörpers ausführen kann, kann eine Person mit Hilfe der Hand ihre Handfläche bewegen und orientieren. Daher sind diese beiden Prozesse ähnlich und können als ein gemeinsamer Prozess dargestellt werden - die Erfassung der Handbewegung durch den Manipulator in Echtzeit.


Damit ist die Problemstellung abgeschlossen. Lassen Sie uns nun die Aufgabe analysieren (die Sprache nennt sie nicht "technische Aufgabe"). Es müssen zwei strukturell unabhängige Geräte entwickelt werden: der Manipulator selbst und das am Arm montierte Bewegungsverfolgungsgerät. Darauf folgt der zeitaufwändige Prozess des Erstellens mathematischer Beschreibungen, des Kompilierens eines Algorithmus und des Schreibens von Software. Wir teilen das Projekt in drei Teile:

1. Die Entwicklung des Manipulators
2. Entwicklung eines Geräts zur Verfolgung der Armbewegung
3. Alles andere

Kurz zu jeder der Stufen:

1. Hier ist alles trivial ... Im CAD entwerfen wir die Struktur, führen Zeichnungen von Teilen durch und fertigen und montieren dann. Dann berechnen wir die Kinematik und schreiben unsere eigene Software, die die Low-Level-Aufrufe an die Laufwerke verbirgt.
2. In dieser Phase bestimmen wir die Art der Sensoren, entwerfen einen Schaltplan, stellen eine Leiterplatte her, entwickeln einen Algorithmus zur Bestimmung der Position im Raum und schreiben Software.
3. Eigentlich für die vorherigen Phasen - um den Manipulator dazu zu bringen, dem Besitzer zu gehorchen. Hier entwickle ich einen Algorithmus zum Konvertieren von Koordinaten in das Arbeitsfeld des Manipulators.

1. Die Entwicklung des Manipulators

In diesem Projekt verwenden wir, wie oben erwähnt, einen Manipulator mit 5 Freiheitsgraden. Eine solche Anzahl von Freiheitsgraden reicht aus, weil Sie umfassen drei lineare und zwei rotatorische Verschiebungen. Die letzten beiden sind für die Ausrichtung des Arbeitskörpers erforderlich, da die Richtung von PO im Raum in Form eines Vektors angegeben werden kann und der Vektor definitiv aus zwei Drehwinkeln wiederhergestellt werden kann (ohne Berücksichtigung der Länge). In diesem Fall benötigen wir fünf verallgemeinerte Koordinaten, die der Anzahl der Achsen entsprechen.

Die Verbindungen des Manipulators sind durch kinematische Rotationspaare der fünften Klasse verbunden. Das Design des Manipulators ist für seinen Typ Standard (das kinematische Schema wird am Anfang des Artikels vorgestellt). Es hat ein Festbett, mit dem das Grundkoordinatensystem verbunden ist, einen Drehständer, an dem die verbleibenden beweglichen Glieder befestigt sind, die in einer Kette verbunden sind. Am Endglied (Flansch) ist ein Arbeitskörper angebracht, in diesem Fall seine Nachahmung in Form eines pfeilförmigen Zeigers (siehe Abbildung unten).




Das 3D-Modell wurde in CAD "Compass 3D" erstellt. Teilematerial - 4 mm Sperrholz und PLA für Kunststoffteile. Teile aus Sperrholz wurden auf einer Lasermaschine ausgeschnitten, Teile aus Kunststoff wurden auf einem 3D-Drucker gedruckt. Dynamixel AX-12 Digital Servos werden als Achsantriebe verwendet. Das Aussehen des Manipulators ähnelt einem abscheulichen Insekt, von dem er den Spitznamen "Komar" erhielt.

Die mathematische Beschreibung der Kinematik

In diesem Stadium ist es notwendig, die direkte und inverse Kinematik des Manipulators zu berechnen. Die direkte Aufgabe besteht darin, die Position der Verbindungen relativ zu einem grundlegenden Koordinatensystem unter Verwendung der bekannten Werte der verallgemeinerten Koordinaten (in diesem Fall der Drehwinkel der Verbindungen) zu bestimmen. Die dazu inverse Aufgabe wird als inverse oder inverse Kinematik bezeichnet. Sie besteht darin, die Parameter der verallgemeinerten Koordinaten zu bestimmen, um die gewünschte Position und Ausrichtung des Arbeitskörpers des Manipulators zu erreichen.

Beginnen wir mit der Berechnung der inversen Kinematik. Lassen Sie uns das geometrische Schema des Manipulators darstellen, aus dem die für uns interessanten geometrischen Beziehungen deutlich werden.



Die gewünschte Position wird durch einen Radiusvektor dargestellt $$$\ vec {r}$ . Es lohnt sich zu erklären, warum der Vektor $$$\ vec {r}$ zum Flanschpunkt und nicht zum Endpunkt des RO gezogen. Da uns die Ausrichtung des Arbeitskörpers im Voraus bekannt ist (ich selbst bestimme sie anhand einiger Anforderungen), muss sich der Flanschpunkt an der richtigen Stelle befinden, angegeben als Vektor $$$\ vec {r}$ . Dieser Vektor wird durch Subtrahieren vom Radiusvektor erhalten $$$\ vec {R}$ gezeichnet zum Endpunkt von PO, seinem Orientierungsvektor $$$\ vec {v_0}$ relativ zu BSK, d.h.

$$

$$\ vec {r} = \ vec {R} - \ vec {v_0}$$

Betrachten Sie den Übergang des Flanschpunktes zur gewünschten Position. Dies geschieht durch Drehen der Glieder a und b (ich habe sie in Form von Vektoren dargestellt) in den Scharnieren A , B und C. Der Ursprung des Basiskoordinatensystems (BSC) liegt am Punkt des Scharniers B. Die Drehachse des Scharniers A ist entlang der Z- Achse gerichtet, die Achsen B und C sind senkrecht zu Z gerichtet .

Wenn alle Formalitäten erfüllt sind, kommen wir zum Punkt. Um das Problem der inversen Kinematik zu lösen, habe ich aufgrund der Einfachheit des Manipulator-Designs einen geometrischen Ansatz verwendet. Aus der Geometrie ist ersichtlich, dass der Vektor $$$\ vec {r}$ gleich der Summe der Verbindungsvektoren $$$\ vec {a}$ und $$$\ vec {b}$ . Winkel $$$\ theta$ , $$$\ gamma_1$ , $$$\ gamma_2$ - die Drehwinkel der Glieder A , B und C.
Betrachten Sie ein Dreieck, das durch Vektoren begrenzt ist $$$\ vec {r}$ , $$$\ vec {a}$ und $$$\ vec {b}$ . Aus diesem Dreieck finden wir nach dem Kosinussatz die Winkel $$$\ alpha$ und $$$\ beta$ . Die Längen der Vektoren seien gleich:

$$

$$| \ vec {r} | = r \ quad | \ vec {a} | = a \ quad | \ vec {b} | = b$$

Wir schreiben den Kosinussatz bezüglich der gewünschten Winkel:

$$

$$b ^ 2 = a ^ 2 + r ^ 2-2ar \ cos (\ alpha) \\ r ^ 2 = a ^ 2 + b ^ 2-2ab \ cos (\ beta)$$

Drücken Sie die Winkel aus $$$\ alpha$ und $$$\ beta$ ::

$$

$$\ alpha = \ arccos \ left (\ frac {a ^ 2 + r ^ 2-b ^ 2} {2ar} \ right) \ quad \ beta = \ arccos \ left (\ frac {a ^ 2 + b ^ 2) -r ^ 2} {2ab} \ right)$$

Aus dem geometrischen Diagramm ist ersichtlich, dass:

$$

$$\ theta = \ arctan = \ left (\ frac {r_y} {r_x} \ right) \ quad \ omega = \ arcsin = \ left (\ frac {r_z} {r} \ right)$$

Dann:

$$

$$\ gamma_1 = \ omega + \ alpha \ quad \ gamma_2 = 180 ^ \ circ- \ beta$$

Schließlich wird der Übergang von einer linearen Koordinate zu den Drehwinkeln der Verbindungen durch die folgenden Formeln ausgeführt:

$$

$$\ theta = arctan \ left (\ frac {r_y} {r_x} \ right) \\ \ gamma_1 = arcsin \ left (\ frac {r_z} {r} \ right) + arccos \ left (\ frac {a ^ 2) + r ^ 2-b ^ 2} {2ab} \ rechts) \\ \ gamma_2 = 180 ^ \ circ-arccos \ links (\ frac {a ^ 2 + b ^ 2-r ^ 2} {2ar} \ rechts)$$

Nachdem Sie den Flanschpunkt in die gewünschte Position gebracht haben, müssen Sie den Arbeitskörper richtig ausrichten. Dazu müssen Sie die Koordinaten des Vektors kennen $$$\ vec {v}$ relativ zum Flanschpunkt, d.h. Koordinaten auf Basis des lokalen Koordinatensystems (LSC) - $$${E '}$ , dessen Anfang sich am Flanschpunkt des Manipulators befindet.

$$

$$E '= \ left [\ vec {x}' \ \ vec {y} '\ \ vec {z}' \ right]$$

Vektor $$$\ vec {x} '$ gerichtet durch Link b , Vektor $$$\ vec {y} '$ - entlang der Schwenkachse f1 .
Eine Basis finden $$$E '$ Wir definieren die Übergangsmatrix von BSK (mit Basis) $$$E_0$ ) und LSK. Diese Matrix wird durch eine Kombination von Drehungen in den Scharnieren A , B und C erhalten :

$$

$$E '= CE_0$$

wo

$$

$$C = R_CR_BR_A$$

Weil Matrix $$$E_0$ ist Single, dann:

$$

$$E '= C = R_CR_BR_A$$

Matrix $$$C$ Sie wird berechnet, indem die Rotationsmatrizen um die Achse mit einem Winkel multipliziert werden.
Wir definieren eine Funktion, die diese Matrix berechnet:

$$

$$f = axisAngle2rotMat (Achse, Winkel)$$

Die Achse wird in Form eines Vektors als Spalte der Matrix genommen, die durch vorherige Rotationen erhalten wurde, und die Winkel wurden bereits oben berechnet.

$$

$$C_A = axisAngle2rotMat (E_0 ^ {\ langle3 \ rangle}, \ theta) \\ C_ {BA} = R_BC_A = axisAngle2rotMat (C_A ^ {\ langle2 \ rangle}, \ gamma_1) C_A \\ C_ {CBA} = R_CC_ { BA} = axisAngle2rotMat (C_ {BA} ^ {\ langle2 \ rangle}, \ gamma_1) C_ {BA}$$

Als Ergebnis erhalten wir:

$$

$$C = C_ {CBA} \ quad E '= C$$

Lassen Sie den Vektor des Arbeitskörpers in BSK $$$\ vec {v_0}$ . Dann ist die Gleichheit wahr:

$$

$$\ vec {v_0} = E '\ vec {v}$$

Von hier aus drücken wir aus $$$\ vec {v}$ - Vektor des Arbeitskörpers in der Basis $$$E '$ d.h. relativ zum Flanschpunkt:

$$

$$\ vec {v} = E '^ T \ vec {v_0}$$

Wenn wir nun den PO-Vektor kennen, können wir die Drehwinkel der Orientierungsachsen f1 und f2 berechnen


Um die Bestellung an eine bestimmte Position zu verschieben, müssen Sie eine Drehung an den Ecken vornehmen $$$\ varphi_1$ und $$$\ varphi_2$ . Die Abbildung zeigt das

$$

$$\ varphi_1 = arctan \ left (\ frac {v_y} {v_z} \ right) \ quad \ varphi_2 = arcsin \ left (\ frac {\ sqrt {v_y ^ 2 + v_z ^ 2}} {V} \ right)$$

wo $$$V = | \ vec {v} | = \ sqrt {v_x ^ 2 + v_y ^ 2 + v_z ^ 2}$ - die Länge des Arbeitskörpers,
$$$v_x, v_y, v_z$ - Vektorkoordinaten $$$\ vec {v}$ .

Die Software des Manipulators ist in zwei Ebenen unterteilt: obere und untere. Die obere Ebene ist in Matlab in Form einer Bibliothek und verschiedener Befehlsmethoden geschrieben, die untere - auf dem Atmega328-Mikrocontroller. Die Aufgabe der oberen Ebene besteht darin, die an den Mikrocontroller gesendeten Befehle zu formulieren. Seine Aufgabe ist es, das Team zusammenzubringen und die Laufwerke entsprechend an der richtigen Position zu installieren. In dieser Form erwies sich das Steuerungssystem als zuverlässig (bisher ...) und bequem zu bedienen.


Die Formulierung des Befehls und das Senden von der oberen Ebene lautet wie folgt: Der Benutzer im Befehlsfenster Matlab ruft eine Funktion aus der Bibliothek auf (z. B. die Funktion, einfach zu einem Punkt zu wechseln) und gibt die erforderlichen Argumente an (normalerweise sind dies die Koordinaten und die Ausrichtung der Bestellung). Nach den oben beschriebenen mathematischen Überlegungen, die in der Bibliothek aufgezeichnet sind, werden die Drehwinkel der Achsen und gegebenenfalls die Drehzahl berechnet. Nach einem einfachen Protokoll stellen wir den Befehl zusammen und senden ihn über die serielle COM-Schnittstelle an den Mikrocontroller der unteren Ebene.

Ein paar Worte zur schriftlichen Bibliothek. Es stehen folgende Funktionen zur Verfügung:

1. serielle Verbindungsfunktionen
2. Bewegungsfunktionen

• bis zu einem Punkt mit einer konstanten Geschwindigkeit aller Antriebe
• bis zu einem Punkt mit einem Endanschlag aller Antriebe (die Geschwindigkeit des Antriebs wird proportional zu seinem eigenen und größten Drehwinkel ausgewählt. Somit hören alle Antriebe am Ende der Annäherung an den Punkt auf, sich zu bewegen).
• bis zu einem Punkt mit einer gleichmäßigen Bewegung jedes Antriebs (in diesem Fall sieht der Geschwindigkeitsgraph wie ein Trapez mit Bereichen wie Beschleunigung, konstante Geschwindigkeit und Bremsen aus)
  
  
  Grafik

  

  
  
  
  
• bis zu einem Punkt gemäß manuell festgelegten Drehwinkeln der Achsen und Drehzahl

Die Liste der Funktionen kann natürlich erweitert werden, aber diese Funktionalität reichte aus, um das Problem, für das der Manipulator entwickelt wurde, direkt zu lösen.

Das Video zeigt die Bedienung des Manipulators.

2. Entwicklung eines Geräts zur Verfolgung der Armbewegung

Fahren Sie mit dem nächsten Schritt fort. Hier müssen Sie ein spezielles Gerät entwerfen, das die Position in Ihrer Handfläche in Echtzeit verfolgen kann. Dieser Vorgang wird auch als "Bewegungserfassung" bezeichnet. Um den Plan umzusetzen, entschied ich mich für das Strapdown-Trägheitsnavigationssystem (SINS), das auf drei Sensoren basiert: einem Gyroskop, einem Beschleunigungsmesser und einem Magnetometer. Eine Reihe dieser Sensoren wird IMU genannt - ein Sensor (in der Übersetzung ist dies die gleiche SINS).

Zuerst habe ich eine Leiterplatte mit der von mir benötigten Funktionalität entworfen, auf der ich diese drei Sensoren platziert habe. Als Verarbeitungscontroller habe ich den Atmega2560-Mikrocontroller ausgewählt (oder eher genommen). Auf dem chinesischen Markt übliche und billige Sensoren. Dies sind gepaarte Sensoren, dreiachsiges Gyroskop und Beschleunigungsmesser MPU6050 und Magnetometer HMC5883l.



Der Algorithmus zur Berechnung der Position im Raum ist recht einfach: Zunächst bestimmen wir die Ausrichtung in Form einer Basis für das lokale Koordinatensystem (LSC), das mit den Sensoren und letztendlich mit der Handfläche verbunden ist.



Die Ausrichtung wird relativ zum anfänglichen Koordinatensystem (NSC) bestimmt, das im Wesentlichen die Anfangsposition des Geräts zum Zeitpunkt des Einschaltens ist. Die Basen von NSC und LSC bestehen aus Spaltenvektoren seines orth:

$$

$$E_0 = \ left [\ vec {X} \ \ vec {Y} \ \ vec {Z} \ right] = \ left [\ begin {array} {cccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] \\ E '= \ left [\ vec {x}' \ \ vec {y} '\ \ vec {z}' \ right]$$

Sie sind durch das Verhältnis verbunden:

$$

$$E '= CE_0$$

Wo $$$C$ Ist eine Übergangsmatrix, ist es auch eine Rotationsmatrix im Raum. Wir betrachten die Basis des NSC als Identitätsmatrix. Deshalb

$$

$$E '= C$$

.
Danach der Beschleunigungsvektor $$$\ vec {A}$ , die in Bezug auf LSC bekannt ist, muss im NSC bestimmt werden. Dies erfolgt durch Multiplizieren des Beschleunigungsspaltenvektors mit der LSC-Basis:

$$

$$\ vec {A} = E '\ vec {A}'$$

Dann integrieren wir den erhaltenen Beschleunigungsvektor zweimal über die Zeit und erhalten die Entfernung, d.h. Koordinaten:

$$

$$\ vec {r} = \ iint \ vec {A} dt$$

Die ersten Versuche, diesen Algorithmus zu implementieren, waren sehr naiv ... Die Naivität bestand darin, dass ich es nur mit dem Gyroskop für möglich hielt, mithilfe der diskreten Integration eine Rotationsmatrix um die Achse zu erhalten. Die Achse kann in diesem Fall als Pseudovektor der Winkelgeschwindigkeit betrachtet werden, deren Komponenten (Projektion auf die Achse) vom Kreiselsensor ausgegeben werden. Und der Winkel wird wiederum durch Integrieren des Vektormoduls erhalten. Die anfängliche Begeisterung und Begeisterung verschwand, als ich eine ungeheure Größe sah, die sogenannte „Null-Drift“, die durch den akkumulierten Fehler aufgrund des Fehlers der diskreten Integration und des Eigenrauschens des Sensors verursacht wurde. Schon damals hatte ich den Gedanken, dass man nach dem Beschleunigungsmesser, der in Ruhe den Vektor zeigt, die Umkehrung des Beschleunigungsvektors der Schwerkraft (im Folgenden als Schwerkraftvektor bezeichnet), die Matrixkorrektur vornehmen kann, aber hier besteht Unsicherheit mit der Tatsache, dass die Korrektur möglich ist nur bis zur Drehung des Winkels um die Z-Achse. Die Korrektur ist abgeschlossen, wenn es möglich ist, die Rotationsmatrix auf alternative Weise wiederherzustellen, d. h. ohne Kreiseldaten zu verwenden.


Dann ist es notwendig, einen anderen Faktor zu verwenden, mit dem eine vollständige Anpassung der Situation möglich ist. Dieser Faktor ist das Erdmagnetfeld, das sich zusammen mit der Schwerkraft an einem einzelnen Punkt auf dem Planeten (natürlich kurzfristig) nicht mit der Zeit ändert. Sie wird mit dem oben genannten Sensor HMC5883l gemessen. In diesem Fall haben wir zwei Vektoren, die ausreichen, um die Position im Raum relativ zu ihnen zu bestimmen.

Nun stellt sich eine logische Frage: "Wie geht das?" Nach erfolglosen Versuchen, diese Frage zu beantworten, stieg ich selbst ins Internet, wo ich die benötigten Informationen fand. Die Aufgabe, die Orientierung im Raum anhand von drei Messungen (Winkelgeschwindigkeit, Schwerkraftvektor und Magnetfeldvektor) zu bestimmen, ergibt sich auch bei der Konstruktion von Amateurflugzeugen (z. B. Coptern), so dass dieses Problem wiederholt mit verschiedenen Methoden gelöst wurde. Eine beliebte Methode ist der sogenannte Majwick-Filter (Sebastian OH Madgwick). Nachdem ich den Originalartikel gelesen und kein Englisch verstanden hatte, wandte ich mich einer wunderbaren Übersetzung zu (danke an den Autor für die geleistete Arbeit). Während ich mich mit dem Studium des Artikels befasste, kam mir immer häufiger die Idee, meinen eigenen Filteralgorithmus zur Positionsbestimmung zu schreiben, da mein Kenntnisstand in diesem Bereich zu diesem Zeitpunkt erheblich zugenommen hatte. Aus Gründen des Interesses „erfinden Sie ein Fahrrad“! Und ich habe es „erfunden“. Unten gebe ich meine Argumentation.

Der Algorithmus verwendet die Messwerte aller drei Sensoren. Ich möchte Sie daran erinnern, dass die Aufgabe des Algorithmus darin besteht, die Ausrichtung des Objekts zu berechnen und die Nulldrift des Gyroskops bei gegebenem Paar aus Beschleunigungsmesser und Magnetometer zu kompensieren. Als mathematisches Werkzeug zur Beschreibung der Position wird eine Quaternion verwendet, weil Im Gegensatz zu Matrizen ist es praktisch, den Algorithmus zu konstruieren und zu optimieren, und erfordert weniger mathematische Operationen, um ihn zu berechnen. Die Quaternion der Rotation im Raum ist wie folgt:

$$

$$q = \ left [q_1 \ q_2 \ q_3 \ q_4 \ right]$$

Kenntnis der durch den normalisierten Vektor beschriebenen Rotationsachse $$$\ vec {v} = \ left [v_x \ v_y \ v_z \ right]$ und Winkel $$$\ varphi$ (wo sie von oben kommen) Sie können die Quaternion berechnen:

$$

$$q_ {v, \ varphi} = \ left [\ cos \ left (\ frac {\ varphi} {2} \ right) \ \ v_x \ sin \ left (\ frac {\ varphi} {2} \ right) \ \ v_y \ sin \ left (\ frac {\ varphi} {2} \ right) \ \ v_z \ sin \ left (\ frac {\ varphi} {2} \ right) \ right] \ quad (*)$$

Dann berechnen wir bei jeder Iteration des Zyklus unter Verwendung nur des Gyroskops den aktuellen Wert der Quaternion gemäß dem Ausdruck:

$$

$$q_n ^ G = q_ {n-1} q_ {v, d \ varphi}$$

Hier $$$q_n ^ G$ - Quaternion zu einem bestimmten Zeitpunkt. Der Index G oben zeigt an, dass sich dieser Wert auf die gemessenen relativ zu den Kreiselwerten bezieht, d. H. Winkelgeschwindigkeit; $$$q_ {n-1}$ - den Wert der Quaternion zum vorherigen Zeitpunkt; $$$q_ {v, d \ varphi}$ - Wenn wir die Position in einem Messschritt ändern, können wir eine diskrete Änderung der Position um einen Winkel sagen $$$d \ varphi$ für $$$dt$ Wird die Abtastperiode durch die Rotationsquaternion (*) ausgedrückt?

Der nächste Schritt bei der Berechnung besteht darin, die Rotationsmatrix basierend auf Daten von einem Paar Beschleunigungsmesser- und Magnetometersensoren zu finden. Insbesondere betrachten wir den Schwerkraftvektor und den Induktionsvektor des Erdmagnetfelds, die, wie oben erwähnt, in Bezug auf die Erde und den zugehörigen NSC statisch sind. Hier lautet die These: Wenn wir die Werte von Schwerkraft und Induktion auf der Grundlage des LSC und des NSC kennen, können wir die Übergangsmatrix (Rotation) vom NSC zum LSC und die Quaternion der Rotation im Raum berechnen .

Bezeichnen mit $$$\ vec {G}$ normalisierter anfänglicher Schwerkraftvektor. Es kann wie folgt angenommen werden:

$$

$$\ vec {G} = {\ left [0 \ 0 \ 1 \ right]} ^ T$$

Durch $$$\ vec {H}$ bezeichnen den normalisierten anfänglichen magnetischen Induktionsvektor:

$$

$$\ vec {H} = {\ left [H_x \ H_y \ H_z \ right]} ^ T$$

Ein dritter Vektor ist ebenfalls erforderlich. $$$\ vec {K}$ was mit diesen beiden verbunden ist. Es wird durch Vektormultiplikation erhalten $$$\ vec {H}$ auf $$$\ vec {G}$ ::

$$

$$\ vec {K} = {\ left [K_x \ K_y \ K_z \ right]} ^ T = \ vec {H} \ times \ vec {G} = {\ left [H_y \ -H_x \ 0 \ right]} ^ T$$

Nun wird die Matrix gebildet $$$M_0$ welches die Ausgangsposition charakterisiert, d.h. NSC, da zum ersten Mal das LSC mit dem NSC übereinstimmt. Die Matrix wird aus den Komponenten der Vektoren erhalten $$$\ vec {H}$ , $$$\ vec {G}$ und $$$\ vec {K}$ ::

$$

$$M_0 = \ left [\ vec {H} \ \ vec {G} \ \ vec {K} \ right] = \ left [\ begin {array} {cccc} H_x & 0 & H_y \\ H_y & 0 & -H_x \\ H_z & 1 & 0 \ end { Array} \ right]$$

In ähnlicher Weise, jedoch bereits bei jeder Iteration der Schleife, wird eine ähnliche Matrix erstellt $$$M '= \ left [\ vec {h} \ \ vec {g} \ \ vec {k} \ right]$ wo $$$\ vec {h}$ Ist der aktuell normalisierte magnetische Induktionsvektor, $$$\ vec {g}$ Ist der aktuelle normalisierte Schwerkraftvektor, $$$\ vec {k} = \ vec {h} \ times \ vec {g}$ . Diese Matrix charakterisiert die Position der LSC, weil Diese Vektoren sind im Koordinatensystem der Sensoren bekannt, das mit der LSC übereinstimmt. Wenn wir dann beide Matrizen kennen, können wir die folgende Gleichung schreiben:

$$

$$E'M '= E_0M_0$$

Es verknüpft zwei Matrizen, die unter verschiedenen Umständen gefunden wurden. Einen Ausdruck gegeben $$$E '= CE_0$ und auf welcher Basis $$$E_0$ Ist die Identitätsmatrix, erhalten wir:

$$

$$CM '= M_0$$

Von hier aus drücken wir die Übergangsmatrix aus $$$C$ ::

$$

$$C = {\ left (M_0 ^ {- 1} \ right)} ^ TM '^ T$$

Der erste Faktor wird, wie Sie verstehen können, nur einmal zu Beginn des Algorithmus berechnet und erfordert keine Nachzählung im Prozess. Der zweite Faktor wird bei jeder Iteration des Zyklus ziemlich leicht und nicht gewaltsam gebildet.

Nachdem die Übergangsmatrix gefunden wurde, wandeln wir sie in eine Quaternion um $$$q_n ^ A$ (Der Algorithmus zum Konvertieren von einer Matrix in eine Quaternion ist eine öffentliche Sache und ich werde ihn hier nicht angeben).

Infolgedessen kennen wir zwei Quaternionen, die unabhängig voneinander gefunden wurden. Und um die Ergebnisse zu kombinieren, habe ich einen einfachen Komplementärfilter mit einem Koeffizienten angewendet $$$F$ , die aus dem Bereich von 0 bis 1 genommen wird:

$$

$$q_n = Fq_n ^ G + \ left (1-F \ right) q_n ^ A$$

Als Ergebnis erhalten wir eine Quaternion, die aktuelle Informationen über die Position des Geräts im Raum mit dem SINS-Modul enthält.

Das Fahrrad ging ... Der Algorithmus funktionierte, aber in einigen Situationen verhielt er sich etwas unangemessen, was im Prinzip nicht störte, aber keinen Grund gab, positiv darüber nachzudenken. Ich habe mein sportliches Interesse befriedigt, und jetzt können Sie sich besser vorgefertigten Lösungen zuwenden. Dann kehrte ich wieder zu dem Artikel von Sebastian Majwik zurück und entschied mich zum Glück, seinen Algorithmus zu verwenden, damit diese wundervolle Person alle Quellcodes auf der Projektwebsite veröffentlichte. Das Archiv enthielt Quellcodes in verschiedenen Sprachen, einschließlich der Matlab-Sprache. Diese Tatsache beeinflusste meine Entscheidung, die Idee aufzugeben, alle Berechnungen auf dem Mikrocontroller durchzuführen (insbesondere da es sich um 8-Bit handelt) und das Programm bereits auf dem Computer in der Matlab-Umgebung zu schreiben. Der Mikrocontroller wird nur zum Abfragen von Sensoren und zum Senden von Daten an einen PC verwendet (eine ähnliche Situation mit dem Manipulator). In diesem Fall basiert der Hauptprogrammcode, der Änderungen und Debugging unterzogen wird, auf der Matlab-Umgebung, was sehr praktisch ist.

Nun, die Orientierung, die wir durch die Quaternion erhalten haben. Was kommt als nächstes nach Plan? Und dann folgen die linearen Koordinaten des Objekts gemäß dem Beschleunigungsmesser. Nun, hier ist es besser einfach zu sagen, dass es unmöglich ist, die Koordinaten mit dem Beschleunigungsmesser mit der erforderlichen Genauigkeit zu bestimmen. Finden Sie zumindest einen Positionswechsel, der angemessen wäre! Natürlich gab es Versuche, dieses Problem zu lösen, aber in Echtzeit war es nicht möglich, die Koordinaten zu finden. Warum? Denn die doppelte diskrete Integration der verrauschten Sensorwerte führte nur zum Flug in die Stratosphäre und mit rasender Geschwindigkeit, aber nicht zu einem positiven Ergebnis. Daher habe ich den am Anfang des Absatzes angegebenen Algorithmus abgeschnitten, bis die Ausrichtung gefunden wurde, und dort angehalten.

3. Alles andere

Also kam ich zur letzten Phase des Entwurfs, nachdem ich genug mit dem Manipulator gespielt und den IMU-Sensor eingewickelt hatte. Während ich an den beiden vorherigen Schritten arbeitete, hatte ich bereits eine klare Vorstellung davon, wie alles funktionieren würde und mit welchem ​​Algorithmus. Deshalb habe ich mich schnell genug mit dieser Phase befasst. Da nur die Ausrichtung der Handfläche bekannt ist, arbeiten wir direkt mit dem Arbeitskörper, der entsprechend ausgerichtet werden muss. RO kann jede Richtung einschlagen, wenn es den Arbeitsbereich nicht verletzt (alle 360 ​​drehen funktioniert nicht).

In dem Punkt über die Entwicklung des Manipulators wurde der Vektor des PO manuell eingestellt, und danach wurden die Drehwinkel der Antriebe gefunden. Dieser Vektor muss also anhand der Ausrichtung der Handfläche bestimmt werden. Orientierung kann als Basis ausgedrückt werden $$$E '$ Finden Sie es, indem Sie das Quaternion in eine Matrix umwandeln. Die Basis besteht aus Spaltenvektoren ihrer Orths, daher erhalten wir drei Vektoren $$$\ vec {x} '$ , $$$\ vec {y} '$ und $$$\ vec {z} '$ . Es ist zweckmäßig, den Vektor als Orientierung zu nehmen $$$\ vec {x} '$ , da ich eine solche Anfangsposition des Manipulators angenommen habe, wenn sich alle Verbindungen und der PO in der XZ-Ebene des Basiskoordinatensystems befinden und der PO zu diesem Zeitpunkt horizontal ist, d.h. Vektor $$$\ vec {v_0}$ Zu Beginn ist es auf die X- Achse des BSK und des NSC ausgerichtet (wir positionieren die Anfangsposition des SINS-Moduls so, dass der NSC mit dem BSK des Manipulators übereinstimmt). In diesem Fall die erste Spalte der Matrix $$$E '$ gleichwertiger Vektor $$$\ vec {v_0}$ . Dann normalisieren wir es entlang der Länge des PO und erhalten den erforderlichen Vektor relativ zum Basiskoordinatensystem des Manipulators. Dann folgen wir der Reihenfolge der Berechnung der verallgemeinerten Koordinaten ab S. 1.

Es ist anzumerken, dass sich der Manipulator beim Ändern der Ausrichtung des RO in zwei Modi bewegen kann: im ersten - wenn der Flanschpunkt stationär ist, im zweiten - wenn der Endpunkt des PO stationär ist, aber seine Ausrichtung beobachtet wird. Der zweite Modus ist interessanter, weil Selbst ohne lineare Bewegung sind immer noch alle Rotationsachsen beteiligt, um den Flanschpunkt zu bewegen, während die Ausrichtung des PO beobachtet wird. Der Übergang vom ersten Modus zum zweiten erfolgt jedoch durch Hinzufügen nur einer Operation zum Subtrahieren von Vektoren, um den Vektor zu finden $$$\ vec {r}$ (siehe Absatz 1).

Alle oben genannten Vorgänge wurden auch in der Matlab-Umgebung programmiert. Im Allgemeinen ist das Programm wie folgt aufgebaut:

1. Kalibrierung beim Start. Wir setzen die gesamte Farm auf ihre ursprüngliche Position und kalibrieren das SINS-Modul für eine bestimmte Menge von Rohdaten, ohne es zu berühren. Eine Kalibrierung ist erforderlich, da Sie den anfänglichen Versatz entfernen müssen, den der Filter erzeugt hat (ich habe nicht verstanden, warum, und es hat einwandfrei funktioniert).
2. Der Anfang des Skripts. Wir initialisieren alle Bibliotheken und Variablen, legen die Anfangsposition des Flansches oder Endpunkts der Bestellung fest.
3. Zyklusstart. Bei jeder Iteration fragen wir die Sensoren ab, finden das Quaternion und übersetzen es in eine Matrix, die die Basis bildet $$$E '$ ist es die Basis, auf der sich der RO befindet. Die erste Spalte dient als Orientierung der PO und wir finden alle verallgemeinerten Koordinaten unter Verwendung der mathematischen Überlegungen aus Abschnitt 1.
4. Wenn wir die verallgemeinerten Koordinaten zum letzten Zeitpunkt und zum gegenwärtigen Zeitpunkt kennen, berechnen wir die Winkeldrehgeschwindigkeit der Achsen.
5. Wir senden ein Datenpaket an den Mikrocontroller des Manipulators.

Es stellte sich natürlich als ungeschickt heraus, aber wenn Sie genauer hinschauen, können Sie ein positives Ergebnis der Studie sehen. Diese Arbeit gibt natürlich nicht vor, fertig zu sein, und erfordert viel Aufwand, um sie zu verfeinern, aber nur, wenn dies verwendet werden kann. Aber ich habe noch keine bestimmte Anwendung gefunden ... Kann mir jemand sagen?