Hallo Habr! In diesem Artikel werde ich über das Erstellen eines mathematischen Modells einer langen Pipeline für das CAE-Programm SimulationX in Modelica sprechen. Es geht darum, Wellenprozesse (Druckpulsationen, Wasserschläge usw.) in einer Hydraulikleitung nach der Methode der Eigenschaften zu berechnen. Trotz der Tatsache, dass diese Methode ziemlich alt ist, gibt es in RuNet nicht genügend Informationen über ihre Anwendung zur Lösung angewandter Probleme.

Im Rahmen des Schnitts werde ich versuchen zu erklären, warum es notwendig ist, Wellenprozesse in Pipelines zu berücksichtigen, um die Probleme hervorzuheben, auf die ich während der Programmierung gestoßen bin, und am Ende werde ich einen Vergleich des Druckpulsationsprozesses geben, wenn eine Hochdruckwasserpumpe mit drei Kolben an einer einfachen langen Pipeline im Modell und auf der URACA arbeitet Deutschland.

Einführung

In der Ingenieurpraxis wird Wellenprozessen in Pipelines in der Regel wenig Beachtung geschenkt. Das bekannteste Beispiel, wenn Wellenprozesse das Leben eines Ingenieurs verderben, ist ein Wasserschlag:



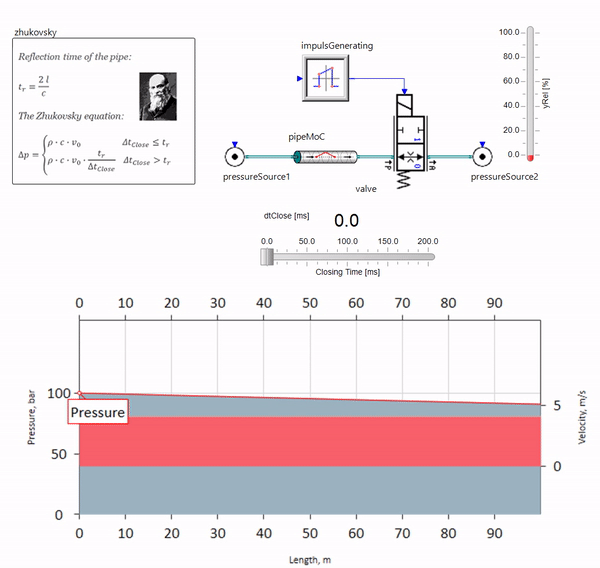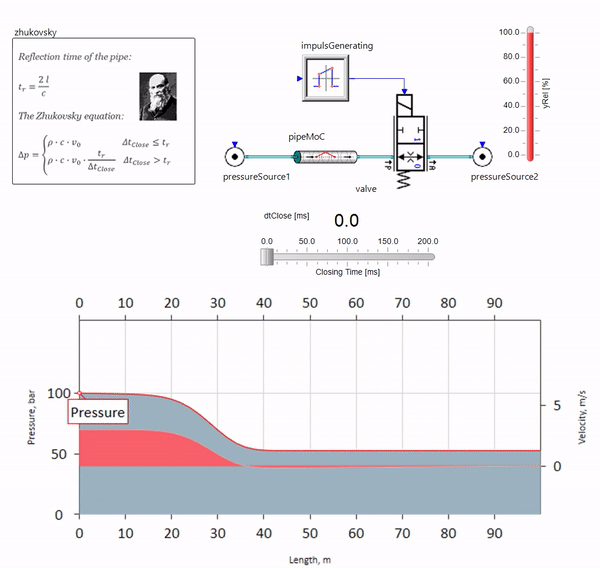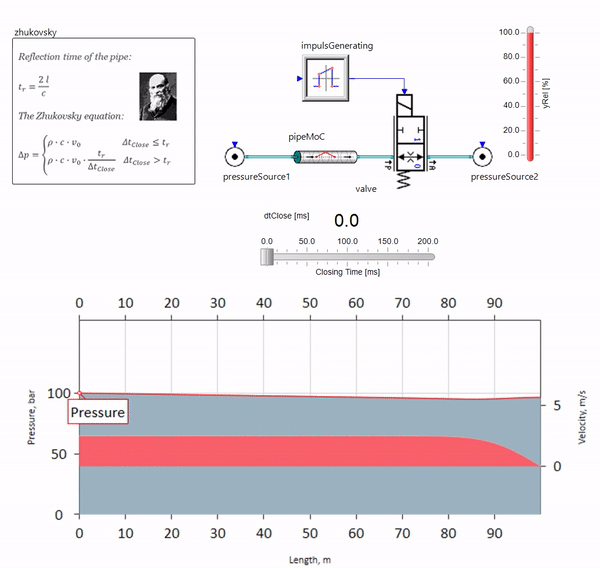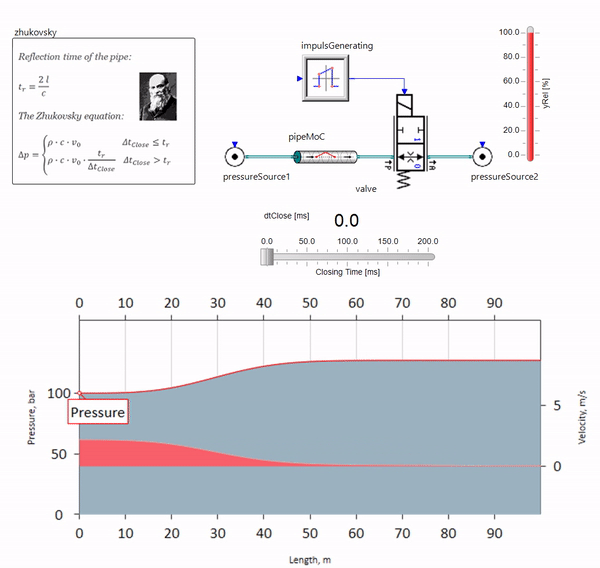
Wenn das Ventil am Ende der Rohrleitung stromabwärts schnell schließt, tritt eine Druckwelle auf, die sich mit der lokalen Schallgeschwindigkeit (für Wasser - ca. 1500 m / s) stromaufwärts bewegt, von der Konstantdruckquelle reflektiert wird, zum Ventil zurückkehrt und von dort reflektiert wird diesmal mit einem negativen Vorzeichen. Dieser Vorgang wird wiederholt, bis die gesamte Energie für die Reibung aufgewendet ist und bis dahin das Ventil und die gesamte Rohrleitung Stoßbelastungen ausgesetzt sind, deren Amplitude und Frequenz von der Länge der Rohrleitung und der Anfangsgeschwindigkeit des Fluidstroms abhängen.

Der Hydroblow mit der Genauigkeit, die zur Lösung praktischer Probleme erforderlich ist, wurde Ende des 19. Jahrhunderts von Nikolai Zhukovsky beschrieben und löste damit das Problem der Unfälle an der Moskauer Wasserversorgung. Seitdem heißt die Formel zur Berechnung des Drucksprungs bei schnellem Schließen des Ventils weltweit die Schukowski-Formel :

$$

$$\ Delta p = \ rho \ cdot c \ cdot \ Delta v$$

In der Praxis manifestiert sich der Wasserschlag in der Regel bei Rohrleitungslängen ab 100 Metern. Bei darunter liegenden Längen ist es bereits schwierig, hydraulische Geräte zu finden, die schneller schließen können als die vom Ventil und zurück übertragene Druckwelle (die Bedingung für das Auftreten eines Wasserschlags). Trotzdem können selbst relativ kurze Rohrleitungen das Leben von Ingenieuren ruinieren, wenn das System eine Quelle für Durchflusspulsationen aufweist (z. B. eine Volumenpumpe mit einer begrenzten Anzahl von Kolben).



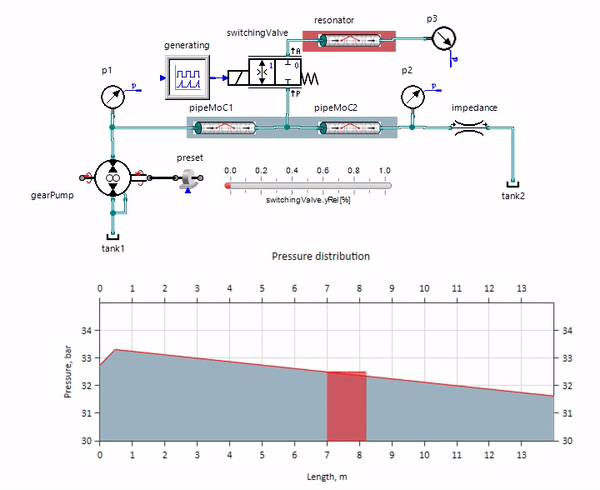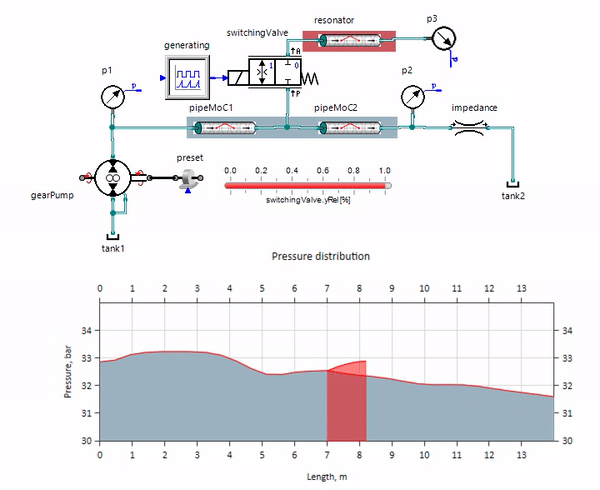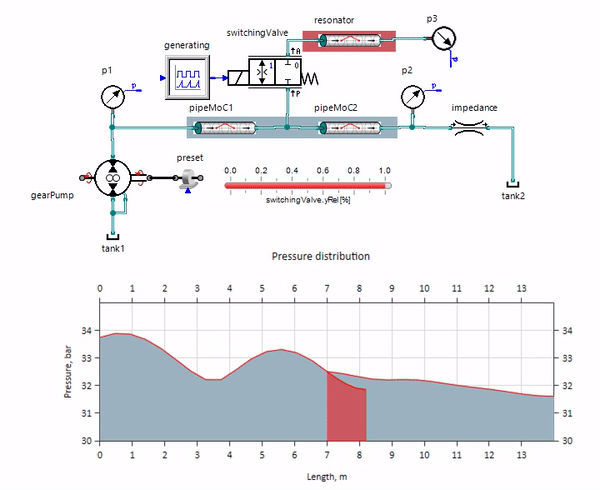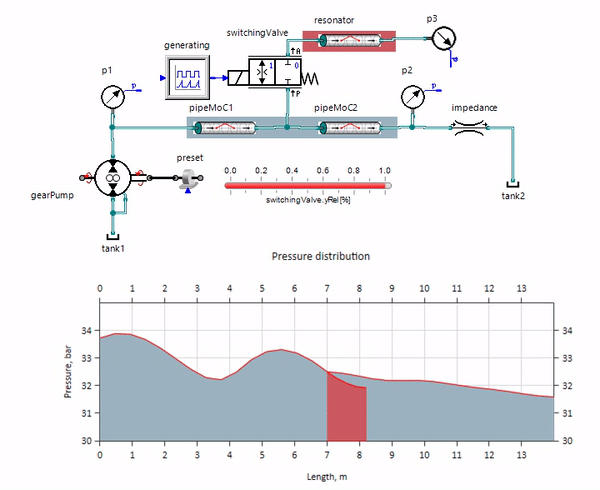
Das GIF zeigt die vorteilhafte Wirkung eines etwas mehr als einen Meter langen Rohrleitungsstücks. Seine Länge entspricht einem Viertel der Druckwellenlänge. Wenn Sie es also an die Hauptleitung anschließen, die sogenannte stehende Welle, die gegenphasig auf die Quelle der Pulsationen trifft und diese auf diese Weise unterdrückt (dies ist der sogenannte Viertelwellen-Pulsationsdämpfer). Es ist klar, dass bei einer unglücklichen Kombination von Umständen der Effekt das Gegenteil sein kann.

In meiner Praxis habe ich lange versucht, Wellenprozesse beiseite zu schieben, weil Ihre Berechnung erforderte ein tieferes Verständnis der matanischen und numerischen Methoden, die ich während meines Studiums mit nachsichtiger Vernachlässigung behandelte. Aber als ich eines Tages mit eigenen Augen sah, dass Standardempfehlungen (eine Hochdruckpumpe überall anzubringen, einen Hydraulikspeicher, eine Sicherung am Pumpeneinlass zu organisieren) weder dazu beitragen, die Pulsationen auf der Bank loszuwerden, noch sie näher an das Verständnis der Prozesse heranzuführen, musste ich tiefer in die Matte eintauchen . Besonders zu meiner Schande hat mein Forschungsleiter bereits begonnen, ein Pipeline-Modell in C ++ für mich zu schreiben.

1. Eindimensionales Modell einer Hydraulikleitung in verteilten Parametern

Das Hauptproblem, das einen zwingt, die Komfortzone traditioneller eindimensionaler Modelle zu verlassen, die durch gewöhnliche Differentialgleichungen beschrieben werden, besteht darin, dass die einfachste Rohrleitung selbst bei den grausamsten Annahmen (vollständig mit Flüssigkeit gefüllt ist, eine konstante Querschnittslänge aufweist, die Flüssigkeitsgeschwindigkeit über den Querschnitt gemittelt wird, Wärmeübertragungsprozesse jedoch nicht berücksichtigt) wird durch Differentialgleichungen in verteilten Parametern (Euler-Gleichungen, nur unter Berücksichtigung der Massenkraft und Reibung auf der rechten Seite der Sekunde) beschrieben avneniya):

$$

$$\ frac {\ partiell \ rho} {\ partiell t} + \ frac {\ partiell (\ rho v)} {\ partiell x} = 0,$$

$$

$$\ frac {\ partiell (\ rho v)} {\ partiell t} + \ frac {\ partiell (\ rho v ^ 2 + p)} {\ partiell x} = \ rho \ cdot (G + F),$$

wo $$$\ rho$ - Dichte $$$v$ - Geschwindigkeit $$$p$ - Druck $$$F$ - Reibungsverluste, $$$G$ - Druckabfall durch Schwerkraft.

Das heißt, Jetzt integrieren müssen Sie nicht nur rechtzeitig $$$t$ sondern auch in räumlicher Koordinate $$$x$ .
Bei Flüssigkeiten können Sie Ihr Leben ein wenig vereinfachen, wenn Sie die Gleichungen von konservativen Variablen in primitive Variablen (Geschwindigkeit und Druck) umschreiben:

$$

$$\ frac {\ partielles p} {\ partielles t} + v \ frac {\ displaystyle \ partielles p} {\ displaystyle \ partielles x} + \ rho \; c ^ 2 \ frac {\ partielles v} {\ partielles x } = 0$$

$$

$$\ frac {\ partielles v} {\ partielles t} + \ frac1 \ rho \ frac {\ displaystyle \ partielles p} {\ displaystyle \ partielles x} + v \ frac {\ displaystyle \ partielles v} {\ displaystyle \ partielles x} = F + G$$

wo $$$c$ - Schallgeschwindigkeit.

Wenn wir nun akzeptieren, dass die Schallgeschwindigkeit deutlich höher ist als die Geschwindigkeit der Flüssigkeitsbewegung $$$v \ ll c$ (was ohne Kavitation zutrifft), werden die Gleichungen noch etwas einfacher:

$$

$$\ frac {\ partielles p} {\ partielles t} + \ rho \; c ^ 2 \ frac {\ partielles v} {\ partielles x} = 0$$

$$

$$\ frac {\ partielle v} {\ partielle t} + \ frac1 \ rho \ frac {\ displaystyle \ partielle p} {\ displaystyle \ partielle x} = F + G$$

Um diese Gleichungen auf die eine oder andere Weise zu lösen, müssen Sie die Differenzierung in der räumlichen Koordinate beseitigen $$$x$ . Dies kann direkt erfolgen, wenn Sie das räumliche Differential durch ein Finite-Differenzen-Schema ersetzen und im Falle der Zeit einfach zum vollständigen Differential wechseln und sagen, dass die Zustandsparameter innerhalb derselben Zelle nicht von der Koordinate abhängen:

$$

$$\ frac {dp} {dt} = - \ rho \; c ^ 2 \ frac {\ triangle v} {\ triangle x}$$

$$

$$\ frac {dv} {dt} = F + G- \ frac1 \ rho \ frac {\ displaystyle \ triangle p} {\ displaystyle \ triangle x}$$

Diese Gleichungen können nun als gewöhnliche Differentialgleichungen gelöst werden, indem die Länge des Rohrs in viele endliche Volumina unterteilt wird. Dies geschieht beispielsweise im Simscape-Paket in MATLAB Simulink, sodass das Problem bis vor kurzem in SimulationX gelöst wurde.
Etwas auf diese Weise kann natürlich berechnet werden, aber die numerischen Schwankungen, die in diesem Fall auftreten, werden stark behindert:

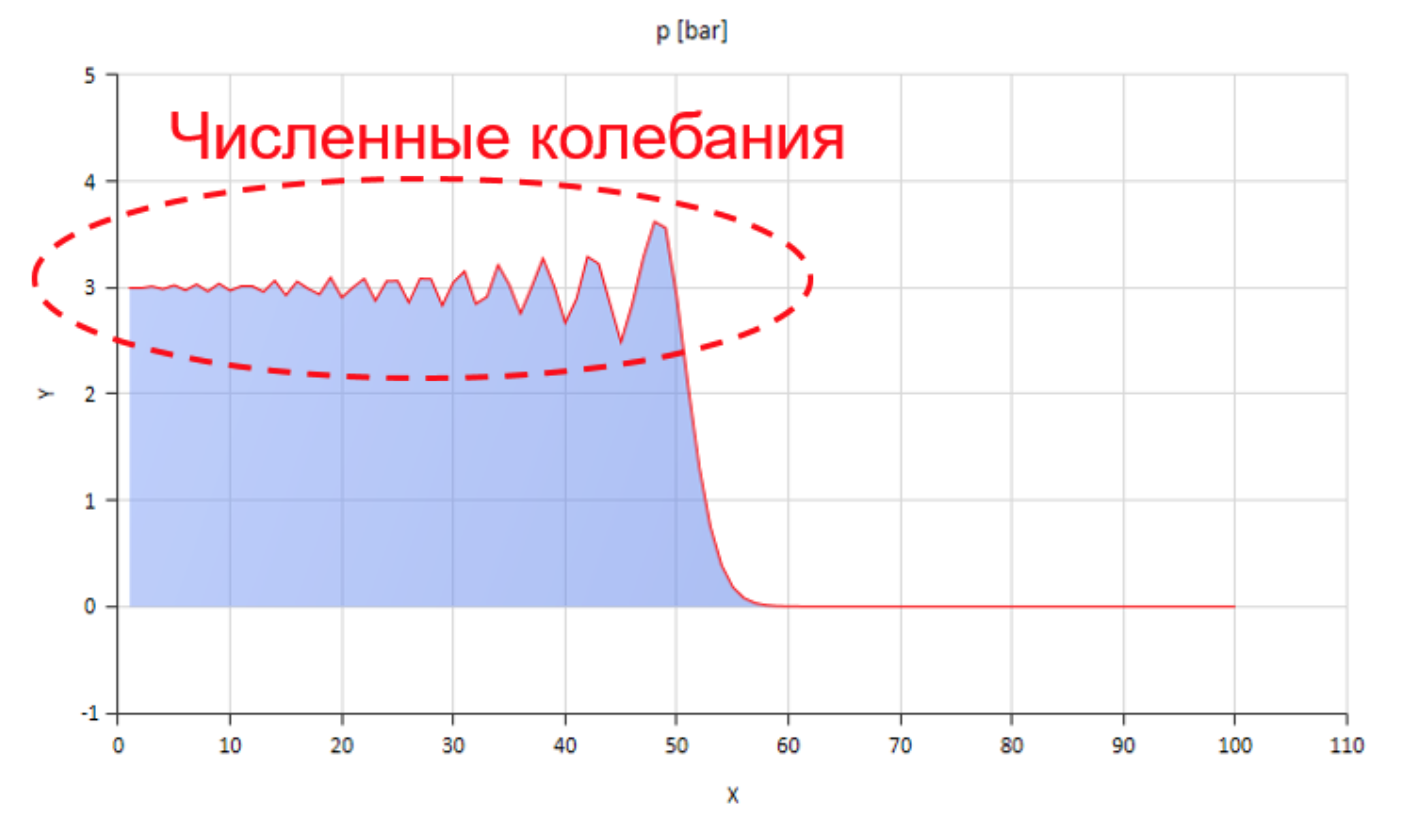Die Abbildung zeigt die Vorderseite der Druckwelle, die sich von links nach rechts bewegt.

Sie können mit diesen Schwingungen umgehen, indem Sie beispielsweise eine numerische Diffusion einführen, aber dann ist die Wellenausbreitungsgeschwindigkeit erheblich verzerrt. Sie können die Reibung erhöhen (insbesondere, um die instationäre Komponente zu erhöhen), aber dann spiegelt das Modell nicht mehr die physikalische Essenz wider.

Es ist am besten, eine andere Methode zum Transformieren von Gleichungen in verteilten Parametern in gewöhnliche Differentialgleichungen zu verwenden, beispielsweise die Methode der Eigenschaften.

2. Charakterisierungsmethode

Wikipedia empfiehlt "Method of Characteristics" empfiehlt:

... um Eigenschaften zu finden, entlang derer sich die partielle Differentialgleichung in eine gewöhnliche Differentialgleichung verwandelt. Sobald gewöhnliche Differentialgleichungen gefunden werden, können sie entlang der Eigenschaften gelöst werden und die gefundene Lösung kann in eine Lösung der ursprünglichen partiellen Differentialgleichung umgewandelt werden.

Es ist wie der Stein eines Philosophen, aber anstatt Metalle in Gold umzuwandeln, verwandeln wir partielle Differentialgleichungen in gewöhnliche und umgekehrt. Es stellt sich die Frage: "Wie kann man das in der Praxis anwenden?" Und vorzugsweise effektiver als mittelalterliche Alchemisten ...

Zunächst werden wir die Problemstellung verstehen. In unserem ersten Moment haben wir eine Art Verteilung von Drücken und Geschwindigkeiten entlang der Länge des Rohrs. Zuerst brechen wir das Rohr in eine endliche Anzahl von Elementen und weisen jeder Fläche einen Druckwert zu $$$p_i$ und Geschwindigkeit $$$v_i$ .


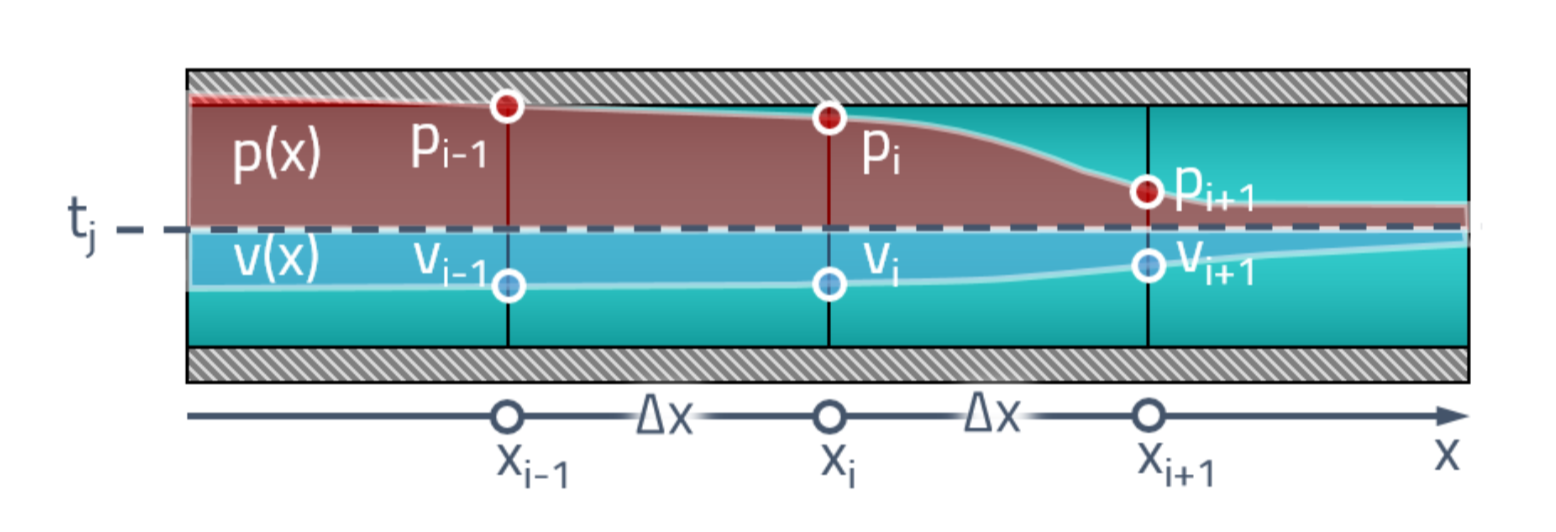
Wir sind daran interessiert, wie sich die Werte an diesen Punkten im Laufe der Zeit ändern $$$\ triangle t$ . Schneller Vorlauf in die Raumzeit und platzieren Sie den Zustand der Pipe in der Zukunft über dem Ausgangszustand:



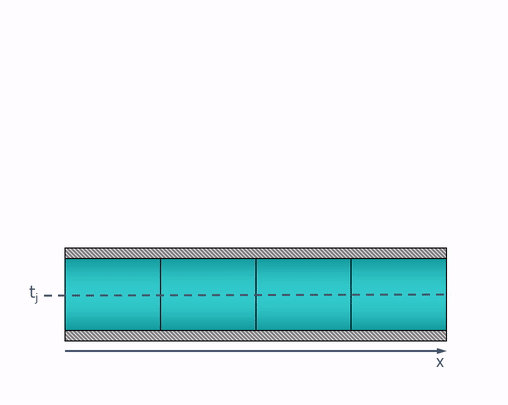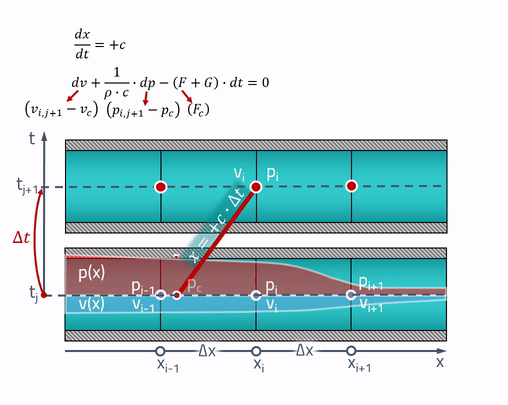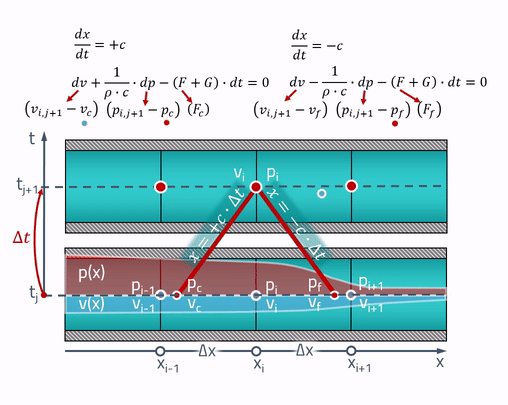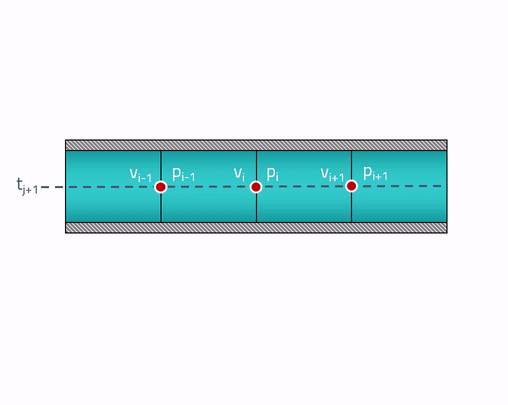
Hier kommen die „magischen“ Eigenschaften zum Tragen! Die Erklärung des arbeitenden Bauern ist, dass alle Änderungen in der Pfeife mit Schallgeschwindigkeit erfolgen. Druck und Geschwindigkeit zum aktuellen Zeitpunkt $$$i$ hängen von Druck und Geschwindigkeit an den Stellen im Rohr ab, an denen die Schallwelle war (würde) $$$\ triangle t$ vor Sekunden. Dies wird wie folgt dargestellt:



Von jedem Punkt werden zwei symmetrische Linien gezogen, deren Steigung durch die Schallgeschwindigkeit bestimmt wird. Dies sind genau die Eigenschaften, entlang derer partielle Differentialgleichungen zu gewöhnlichen Differentialgleichungen werden. Wenn wir die Punkte, an denen sich die Eigenschaften mit dem Zustand des Rohrs in der Vergangenheit überschneiden, als benennen $$$c$ und $$$f$ sind die Gleichungen wie folgt geschrieben:

$$

$$dv + \ frac1 {\ rho c} dp- (F + G) dt = 0 \; für \; \ frac {dx} {dt} = + c$$

$$

$$dv- \ frac1 {\ rho c} dp- (F + G) dt = 0 \; für \; \ frac {dx} {dt} = - c$$

Die Werte von Drücken und Geschwindigkeiten an diesen Punkten können durch lineare Interpolation zwischen den Werten der Zustandsparameter auf dem Gitter erhalten werden:


Es ist wichtig zu beachten, dass sich diese Punkte immer innerhalb der Nachbarzellen befinden sollten! Dafür muss der Zeitschritt das Courant-Friedrichs-Levy-Kriterium (CFL) erfüllen:

$$

$$\ triangle t <\ frac {\ triangle x} c$$

Nun kann zumindest das einfachste Differenzschema auf diese Gleichungen angewendet werden:

$$

$$(v_ {i, \; j + 1} -v_c) + \ frac1 {\ rho c} (p_ {i, \; j + 1} -p_c) - (F + G) \ Dreieck t = 0$$

$$

$$(v_ {i, \; j + 1} -v_f) - \ frac1 {\ rho c} (p_ {i, \; j + 1} -p_f) - (F + G) \ Dreieck t = 0$$

Im resultierenden System zweier Gleichungen zwei Unbekannte: Druck $$$p_ {i, \; j + 1}$ und Geschwindigkeit $$$v_ {i, \; j + 1}$ . Sie können es numerisch lösen, aber es gibt kein besonderes Problem, um eine analytische Lösung zu erhalten. Wenn wir dann die Konstanz der Schallgeschwindigkeit akzeptieren, erhalten wir ein vollständig explizites Differenzschema.

Zur Konsolidierung werde ich eine Animation der Methode der Merkmale geben:

3. Experimentieren

Ich hatte die Gelegenheit, mich endlich an das Modell zu erinnern, als ich bei der ESI ITI GmbH in Dresden anfing. Einmal erhielt ich ein Ticket im Helpdesk, wo sich die URACA- Ingenieure beschwerten, dass sie die Konvergenz mit dem Experiment mit unserer „alten“ Pipe nicht erreichen konnten.
Sie stellen Hochdruck-Wasserkolbenpumpen her, einen so großen „Karcher“, und möchten mögliche Resonanzeffekte aufgrund der Einbeziehung vorhersagen können Wellenprozesse in der Pipeline. Das Problem ist, dass solche Pumpen in der Regel nur sehr wenige Kolben haben und bei niedrigen Drehzahlen (250-500 U / min) arbeiten:



Aufgrund dessen und auch aufgrund des Einflusses der Kompressibilität der Flüssigkeit ist der Ausstoß sehr ungleichmäßig:



Lücken und Nichtlinearitäten erschweren die Linearisierung und Analyse des Modells im Frequenzbereich, und CFD-Berechnungen für eine solche Aufgabe schießen mit einer Kanone auf Spatzen. Darüber hinaus hatten sie bereits Modelle in SimulationX, in denen sie die Dynamik des mechanischen Teils der Pumpe, die Elastizität des Rahmens und die Eigenschaften des Elektromotors berücksichtigten. Daher wäre es interessant zu sehen, wie sich die Pipeline darauf auswirkt.

Das Prüfstandslayout ist recht einfach:



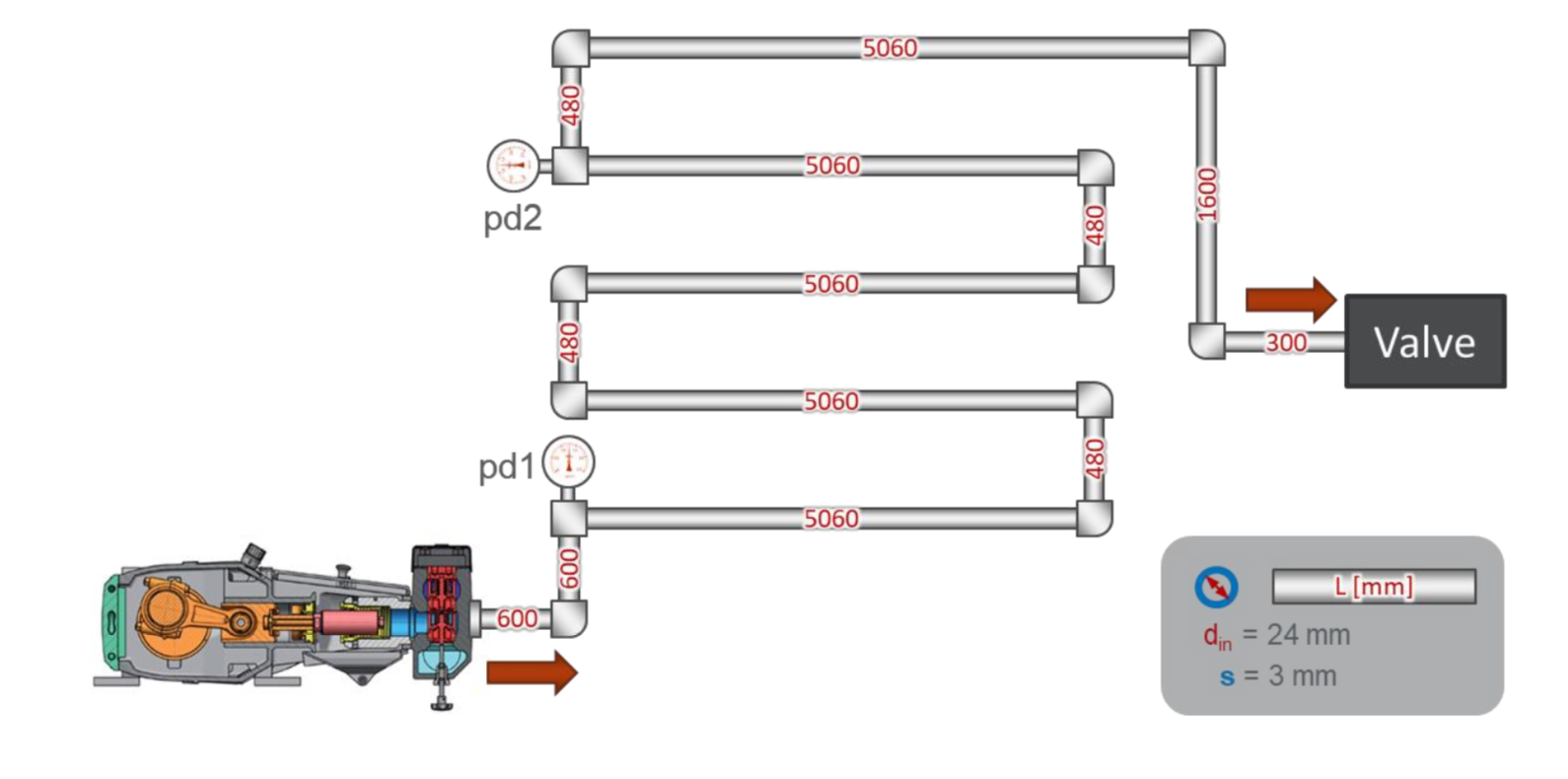
Es gibt eine einfache Pipeline mit einer Gesamtlänge von ca. 30 Metern. Zu Beginn der Rohrleitung ist in einem Abstand von 22 Metern ein Drucksensor pd1 installiert - ein Drucksensor pd2. Am Ende der Rohrleitung befindet sich ein Ventil, das den Druck im System einstellt.

Ich schlug vor, die Beta-Version meines Modells zu testen, da ein solches Modell in SimulationX erstellt wurde:



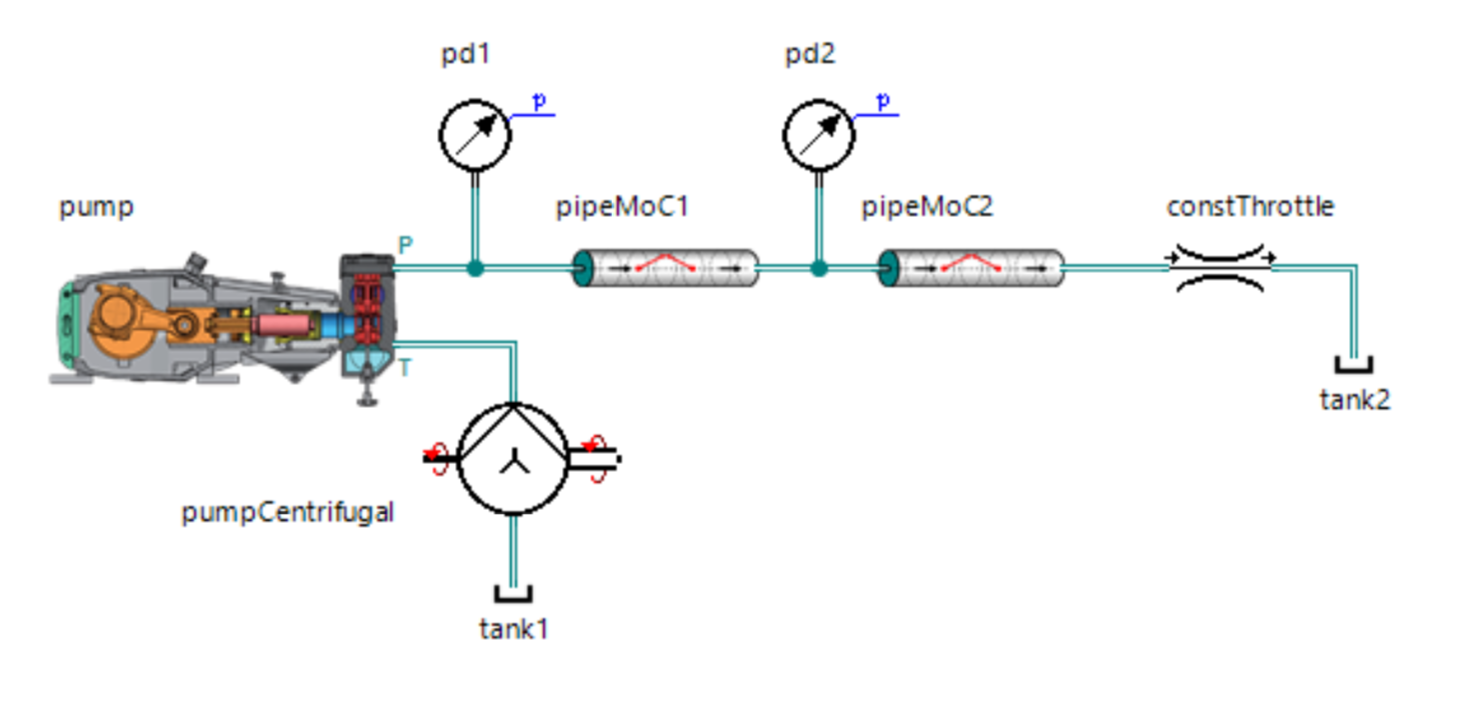
Die Ergebnisse haben mich sogar angenehm überrascht:




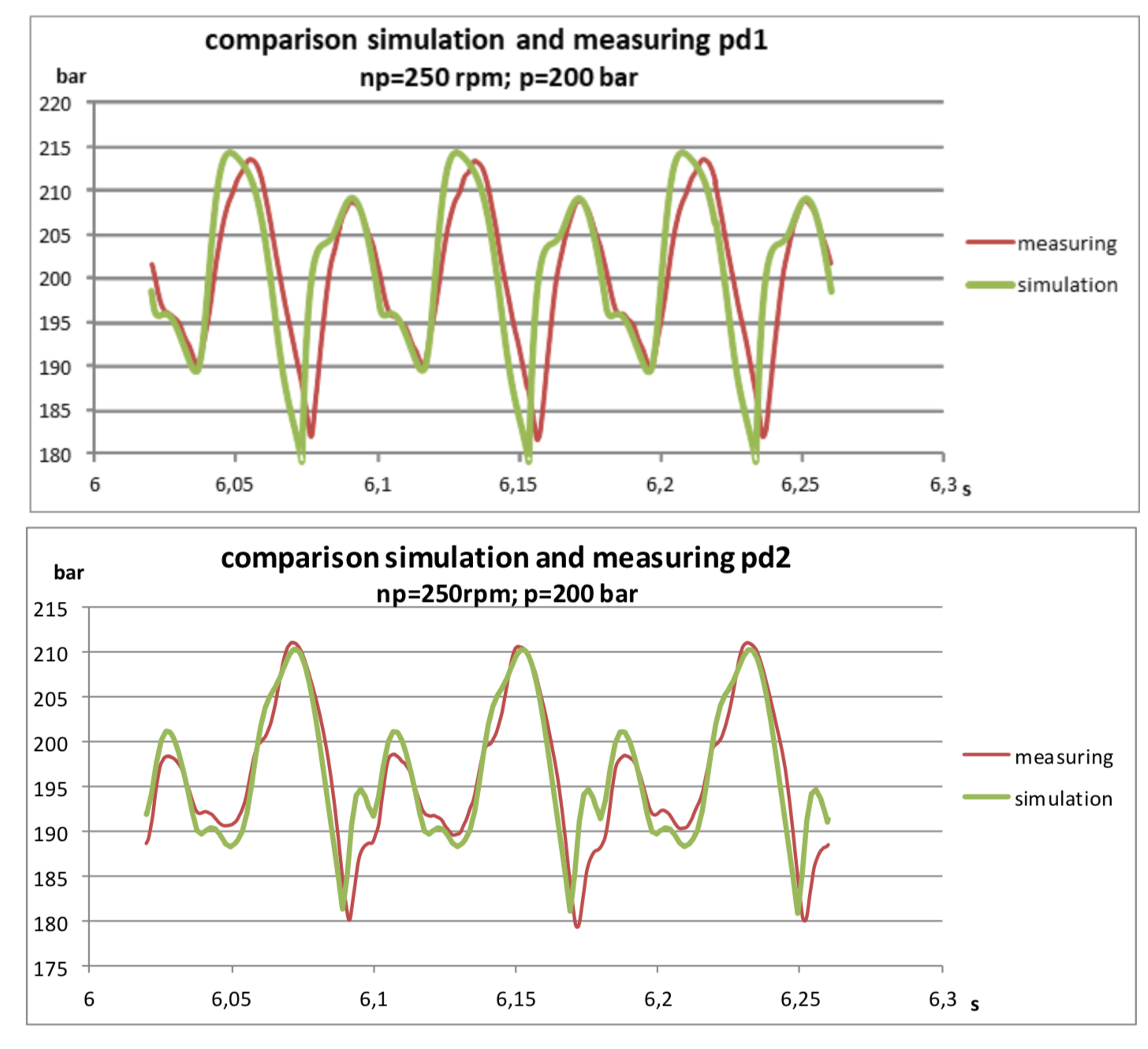
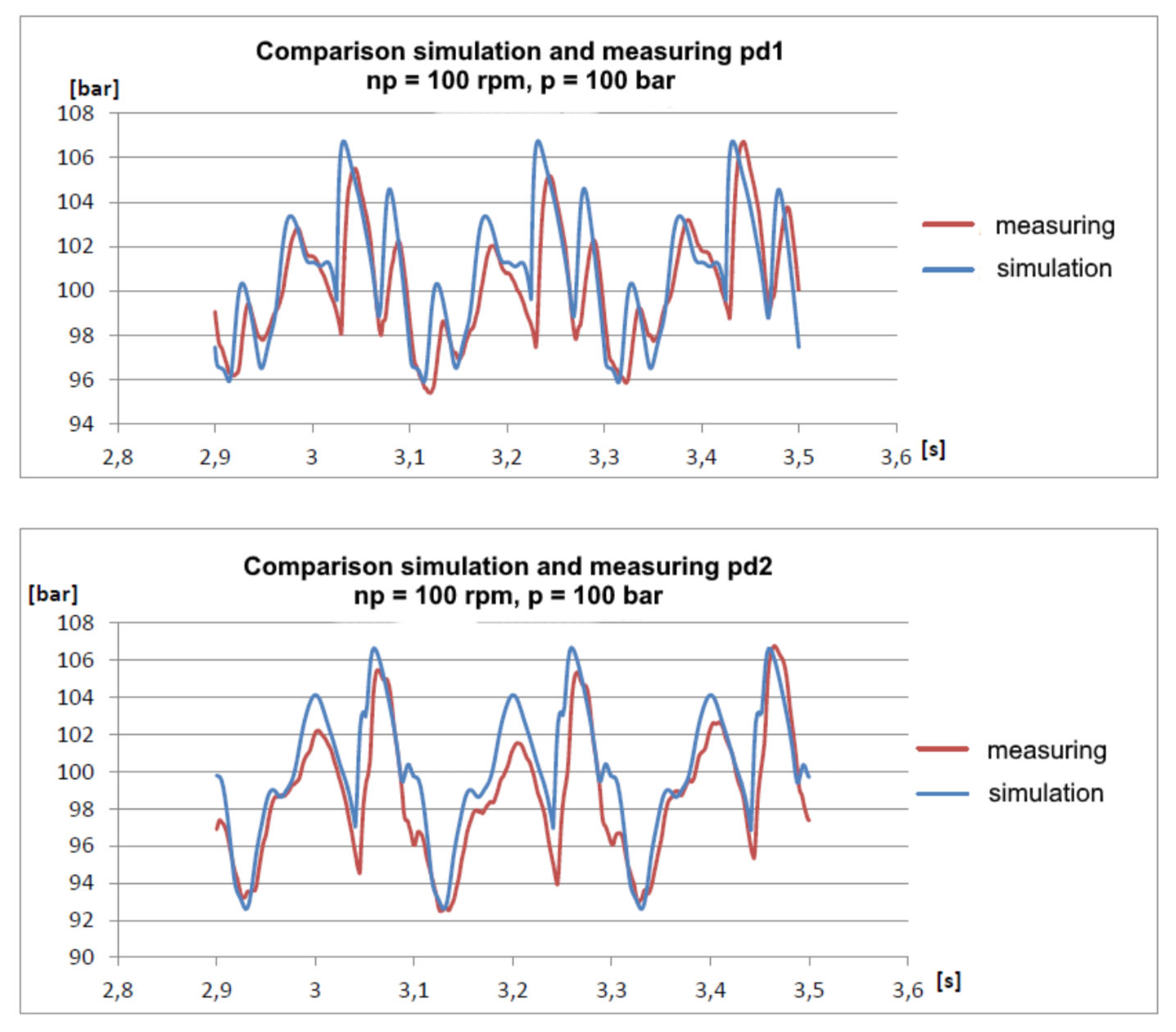
Es ist zu erkennen, dass das Modell leicht gedämpft ist, was verständlich ist, sofern der hydraulische Widerstand nicht berücksichtigt wird. Trotzdem stimmen die Grundschwingungen ziemlich gut überein und ermöglichen es, Druckamplituden mit ziemlich guter Genauigkeit vorherzusagen.

Diese Erfahrung ermöglichte es mir, schnell ein neues Modell der Hydraulikleitung in der SimulationX-Version auf den Markt zu bringen. Ich tauchte in dieses Thema ein und bemerkte nicht, wie ich zusammen mit dem Praktikanten auch das Modell der pneumatischen Leitung sägte, bei dem alles viel interessanter war. Dort musste ich eine Methode verwenden, die auf der Godunov-Methode basiert, die wiederum auf der Lösung des Riemann-Problems des Zerfalls einer willkürlichen Diskontinuität basiert, aber was ist damit ein anderes Mal ...

Literatur

1. In der heimischen Literatur wird die Methode der Eigenschaften für technische Anwendungen am besten in dem Buch "Hydromechanics", D.N. Popov, S.S. Panaiotti, M.V. Ryabinin.
2. In seiner Publikation
   Rohrleitungssimulation nach der Methode der Kennlinien zur Berechnung der Druckpulsation einer Hochdruckwasserkolbenpumpe

   Dr.-Ing. (Rus) Maxim Andreev, Dipl.-Ing. Uwe Grätz und Dipl.-Ing. (FH) Achim Lamparter ”, 11. Internationale Fluidtechnikkonferenz, 11. IFK, 19.-21. März 2018, Aachen, Deutschland, siehe Text in PM
   Ich habe die Probleme der Kopplung der Methode der Eigenschaften und des Lösers der ODE genauer untersucht.
3. Diejenigen, die Zugang zu deutschen Bibliotheken haben, finden in der folgenden Dissertation den besten Überblick über Methoden zur Lösung hyperbolischer Gleichungen für Hydraulikleitungen, die ich getroffen habe: Beck, M., Leiter und Simulation der Wellenbewegung in kavitativen Hydraulikleitungen, Univ. Stuttgart, Deutschland, 2003.
4. Klassiker des Genres der hyperbolischen Gleichungen im Allgemeinen: Randall J. Leveque, Methoden mit endlichem Volumen für hyperbolische Probleme, Cambridge University Press, Cambridge, Vereinigtes Königreich, 2002.