Dynamische Programmierung bei Olympiadenproblemen

Hallo!

Kürzlich habe ich Probleme aus dem Timus Online Judge- Archiv gelöst und bin auf einen Abschnitt namens Dynamic Programming Tasks gestoßen . Diese Art von Aufgabe ist für mich von besonderem Interesse, da dieser Ansatz häufig die Geschwindigkeit und Eleganz der Lösung gewährleistet. Was ist dynamische Programmierung?

Dynamische Programmierung ist ein Ansatz zur Lösung von Problemen, bei denen eine Unterteilung in Teilaufgaben erfolgt, die im Vergleich zur ursprünglichen „einfacher“ sind. Das Wort "dynamisch" hat eine ähnliche Bedeutung wie "induktiv": Es wird angenommen, dass die Antwort für eine bestimmte Bedeutung bekannt ist $$$k$und ich möchte die Antwort finden für $$$k + 1$. In der Mathematik wird dies als induktiver Übergang bezeichnet und ist die Hauptidee der dynamischen Programmierung.

Einfache Beispiele

Die auffälligste und indikativste Aufgabe ist die Aufgabe des Rechnens $$$n$Nummer der Fibonacci-Sequenz. Es ist bekannt, dass die Sequenz die folgenden Eigenschaften hat:

$$

$$F_0 = F_1 = 1, \ F_n = F_ {n-1} + F_ {n-2}.$$

Dies impliziert sofort die Wiederholungsformel:

int Fibonacci(int n) { if(n == 1 || n == 2) return 1; return Fibonacci(n-1) + Fibonacci(n-2); } 

Wenn die Rekursion nach einer Zahl "vom Ende" sucht, berechnet die folgende Methode nacheinander alle dazwischen liegenden Zahlen $$$0$und $$$n$::

 int dpFibonacci(int n) { int prev1 = 1; int prev2 = 1; int curr = 0; for(int j = 2; j < n; j++) { curr = prev1 + prev2; prev1 = prev2; prev2 = curr; } return curr; } 

Es ist klar, dass für ausreichend große $$$n$Dieser Algorithmus arbeitet viel schneller: Er berechnet keine Zwischenwerte mehrmals. Betrachten Sie ein etwas komplexeres Beispiel.

Beispiel 1. Sie gehen auf einer mautpflichtigen Treppe. Auftreten $$$i$Schritt müssen Sie bezahlen $$$a_i$Münzen. Sie können zum nächsten Schritt übergehen oder über einen springen. Aufgabe: bestehen $$$n$Schritte und geben Sie so wenig Münzen wie möglich aus.

Es ist klar, dass wir bei jedem Schritt die Anzahl der „Zahlungen“ minimieren, aber wir können auf einen sehr teuren Schritt stoßen, den wir vermeiden möchten. Erstellen Sie ein Array von Werten $$$d$in dem auf $$$j$-Der Platz ist die (minimale) Anzahl von Münzen, die ausgegeben werden müssen, um dorthin zu gelangen $$$j$th Schritt. Es ist sofort klar, dass $$$d_1 = a_1, \ d_2 = a_2$. Und dann werden wir mindestens die beiden vorherigen Schritte ausführen und die Kosten für den Schritt selbst addieren:

$$

$$d_i = \ min \ left (d_ {i-1}, d_ {i-2} \ right) + a_ {i}.$$

Wir ändern die Bedingungen des Problems ein wenig: Nehmen wir an, dass Sie in einigen Schritten Münzen erhalten können (dies bedeutet das $$$a_k <0$) Was muss im Algorithmus geändert werden, damit das richtige Ergebnis erzielt wird?


Stellen Sie sich ein anderes Beispiel vor, das eine „zweidimensionale“ Dynamik verwendet.

Beispiel 2. Im Labyrinth gibt es $$$n \ times m$Räume, von denen jeder Gold enthält (in einem Käfig $$$(i, j)$Lügen $$$a_ {ij}$Gold). Die Aufgabe besteht darin zu bestimmen, welche maximale Menge Gold mit einer optimalen Route von einem Punkt aus gesammelt werden kann $$$(0,0)$auf den Punkt $$$(n, m)$wenn Sie entweder nach unten oder rechts gehen können.

Wir wollen also den besten Weg zur Zelle kennen $$$(i, j)$. Wir können aus zwei Zellen hierher kommen - $$$(i-1, j)$und $$$(i, j-1)$. Vorausgesetzt, die optimalen Routen für diese beiden Zellen sind bekannt (sie sind in einer Tabelle gespeichert $$$d$), dann die Antwort für die Zelle $$$(i, j)$erhalten wie folgt:

$$

$$d_ {ij} = \ max \ left (d_ {i-1j}, d_ {ij-1} \ right) + a_ {ij}.$$

Dies ist eine weitere klassische dynamische Programmieraufgabe, deren Modifikationen bei Sportprogrammieraufgaben häufig vorkommen. Eine ähnliche Aufgabe wird hier näher erläutert.

Anspruchsvollere Aufgaben

Auf Wunsch kann ein dynamischer Ansatz beliebig angeschraubt werden. Betrachten Sie eine Aufgabe aus dem Timus Online Judge-Archiv.

Die mathematische Formulierung des Problems lautet wie folgt: Es ist erforderlich, die Mindestanzahl von Begriffen zu finden, die erforderlich sind, um eine bestimmte Anzahl in vollständige Quadrate zu zerlegen.

Nehmen wir an, wir kennen nach wie vor die Antworten für alle Zahlen $$$k-1$die in einem Array gespeichert sind $$$d$und wir würden gerne finden $$$d_ {k}$.

Nimm diese Nummer $$$k$und analysieren, welche Situationen sein können:

1. $$$k$ist ein volles Quadrat. In diesem Fall $$$d_ {k} = 1$.
2. Vielleicht die vorherige Nummer $$$k-1$war ein komplettes Quadrat. Dann $$$d_ {k} = d_ {k-1} + 1$.

Im Allgemeinen scheint die Option, eine Einheit zur vorherigen hinzuzufügen, nicht so schlecht zu sein.

Wir gehen wie folgt vor: Wir suchen eine Zersetzung $$$k = q ^ 2 + s$so dass

$$

$$d_ {q ^ 2} + d_s <d_ {k-1} + 1.$$

Als $$$q ^ 2$- dann volles Quadrat $$$d_ {q ^ 2} = 1$und

$$

$$d_s <d_ {k-1},$$

Das heißt, wir haben eine Partition gefunden, die einfach besser ist als $$$d_ {k-1} + 1$und die Antwort in diesem Fall wird sein

$$

$$d_k = d_ {s} + d_ {q ^ 2} = d_s + 1.$$

Betrachten Sie das folgende Problem . Das Ziel ist es, eine Treppe aus zu bauen $$$N$Würfel nach den Regeln:

1. Die Treppe hat mindestens zwei Stufen.
2. Eine Treppe kann nicht zwei identische Stufen haben.
3. Die Stufen der Treppe verlaufen in aufsteigender Reihenfolge (dh die nächste ist größer als die vorherige).

Dieses Mal werden wir eine zweidimensionale Dynamik aufbauen. Erstellen Sie eine Tabelle $$$d$in der die Position $$$(i, j)$die Anzahl der Treppen bestehend aus $$$i$Würfel, deren Höhe nicht überschreitet $$$j$. Wenn es klappt, ist die Antwort auf unser Problem die Summe

$$

$$\ sum \ limit_ {j = 1} ^ n d_ {nj}.$$

Wir werden also das Problem lösen, die Anzahl der Treppen zu ermitteln, aus denen sich die Treppe zusammensetzt $$$i$Würfel, die groß sind $$$j$. Das Bild zeigt die Treppen, die hineinfallen $$$d_ {74}$::

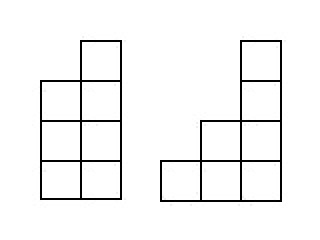
Da wir alle Treppen kennen, die aus weniger Würfeln bestehen, werden wir die Treppen „abspalten“ $$$(i, j)$rechte Spalte. Das Ergebnis ist eine Treppe c $$$i-j$Würfel. Beispiel für $$$i = 9, \ j = 4$::

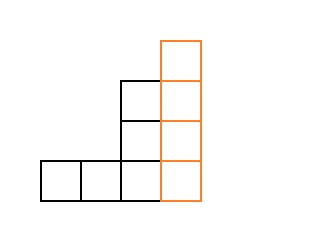
Aber für solche Treppen ist das Ergebnis bereits bekannt, so dass wir alle diese Treppen mit einem Zyklus durch sortieren werden $$$k$und addieren Sie alle Ergebnisse. Auf diese Weise,

$$

$$d_ {ij} = \ sum \ limit_ {k = 1} ^ {j-1} d_ {i-jk}.$$

Jetzt werden wir die Höhen der Treppen sortieren:

$$

$$d_ {ij} = \ sum \ limit_ {k = 1} ^ {j-1} d_ {i-jk}, \ j = \ overline {1, i}.$$

Endlich ändern $$$i$von $$$1$vorher $$$n$Wir bekommen die Antwort.

Wichtig : Bei der Erstellung unserer Matrix ist dies zu berücksichtigen $$$d_ {ii} = 1$, da sonst einige Arten von Treppen „verloren gehen“ (wenn sie „abgespalten“ werden), aber es versteht sich von selbst, dass eine solche Treppe die Bedingungen des Problems nicht erfüllt, lautet die Antwort die Nummer $$$d_ {nn} - 1$.


Die nächste Aufgabe wird mit einem eindimensionalen Array gelöst.

Also was wir haben. Der erste ent kennt 2 Wörter. Jeder ent lehrt alle Wörter, die er selbst kennt, zwei ents: jung und alt. Im Gegenzug wurden den Jungen so viele Wörter beigebracht, wie er bereits weiß, und den Alten wurde nur ein Wort beigebracht. Sie müssen wissen, wie viele Ents genau wissen $$$K$Wörter (es ist notwendig, die Anzahl dieser ents modulo abzuleiten $$$P$)

Die Lösung ist ganz einfach. Erstellen Sie ein Array $$$d$in dem auf $$$i$-th Platz speichern wir die Anzahl der ents (modulo $$$P$) wer weiß $$$i$Worte. Alles beginnt mit dem ersten Ent, der daher zwei Wörter kennt $$$d_2 = 1$. Und dann ist alles einfach:

• Alle Enten, die eine ungerade Anzahl von Wörtern kennen, sind alt und können nur von den vorherigen lernen. Deshalb für ungerade $$$i: \ d_i = d_ {i-1};$
• Was die Ents betrifft, die eine gerade Anzahl von Wörtern kennen, so sind dies alle diejenigen, die die gleiche Anzahl von Wörtern von Elfen (jung) erhalten haben. $$$+$diejenigen, die aus dem Vorherigen gelernt haben (alt); das heißt, für gerade $$$i$wir haben $$$d_i = d _ {{i \ backslash 2}} + d_ {i-1}$.

Es bleibt das Berechnungsmodulo zu behandeln. Um keine großen Zahlen zu speichern, werden wir uns sofort an alle modulo-Werte erinnern.


Verwendete Ressourcen:

1. Timus Online Richter;
2. Ein bisschen über dynamische Programmierung;
3. Vergleichseigenschaften modulo.